Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T10:21:50.925Z Has data issue: false hasContentIssue false
  • English
  • Français

The inverse deformation problem

Part of: Representation theory of groups Structure and classification of infinite or finite groups Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  14 July 2016

Timothy Eardley  and
Jayanta Manoharmayum
Timothy Eardley
Affiliation:
School of Mathematics and Statistics, University of Sheffield, Sheffield S3 7RH, UK email [email protected]
Jayanta Manoharmayum*
Affiliation:
School of Mathematics and Statistics, University of Sheffield, Sheffield S3 7RH, UK email [email protected]
*
[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a commutative complete local noetherian ring 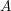$A$ with finite residue field 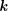$\boldsymbol{k}$, we show that there is a topologically finitely generated profinite group 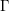$\unicode[STIX]{x1D6E4}$ and an absolutely irreducible continuous representation 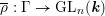$\overline{\unicode[STIX]{x1D70C}}:\unicode[STIX]{x1D6E4}\rightarrow \text{GL}_{n}(\boldsymbol{k})$ such that 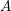$A$ is a universal deformation ring for $\unicode[STIX]{x1D6E4},\overline{\unicode[STIX]{x1D70C}}$.

Keywords

inverse deformation problem

MSC classification

Primary: 20C20: Modular representations and characters 20E18: Limits, profinite groups 11F80: Galois representations
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 8 , August 2016 , pp. 1725 - 1739
Copyright
© The Authors 2016 

References

Bleher, F. and Chinburg, T., Universal deformation rings need not be complete intersections , C. R. Math. Acad. Sci. Paris 342 (2006), 229–232.CrossRefGoogle Scholar
Bleher, F. and Chinburg, T., Universal deformation rings need not be complete intersections , Math. Ann. 337 (2007), 739–767.CrossRefGoogle Scholar
Bleher, F., Chinburg, T. and de Smit, B., Deformation rings which are not local complete intersections, Preprint (2010), arXiv:1003.3143 [math.NT].Google Scholar
Bleher, F., Chinburg, T. and de Smit, B., Inverse problems for deformation rings , Trans. Amer. Math. Soc. 365 (2013), 6149–6165.CrossRefGoogle Scholar
Bonnafé, C., Representations of SL2(F q ), Algebra and Applications, vol. 13 (Springer, London, 2011).CrossRefGoogle Scholar
Brown, K., Cohomology of groups, Graduate Texts in Mathematics, vol. 87 (Springer, New York, 1982).CrossRefGoogle Scholar
Chinburg, T., Can deformations rings of group representations not be local complete intersections? in Problems from the workshop on automorphisms of curves, Rendiconti del Seminario Matematico della Università di Padova, vol. 113, eds Cornelissen, Gunther and Oort, Frans (2005), 129–177.Google Scholar
Cline, E., Parshall, B. and Scott, L., Cohomology of finite groups of Lie type, I , Publ. Math. Inst. Hautes Études Sci. 45 (1975), 169–191.CrossRefGoogle Scholar
de Smit, B. and Lenstra, H., Explicit construction of universal deformation rings , in Modular forms and galois representations, eds Cornell, G., Silverman, J. H. and Stevens, G. (Springer, New York, 1997).Google Scholar
Dorobisz, K., The inverse problem for universal deformation rings and the special linear group. Trans. Amer. Math. Soc., to appear, doi:10.1090/tran6644. Preprint (2013), arXiv:1308.1346 [math.RA].CrossRefGoogle Scholar
Manoharmayum, J., A structure theorem for subgroups of GL n over complete local noetherian rings with large residual image , Proc. Amer. Math. Soc. 143 (2015), 2743–2758.CrossRefGoogle Scholar
Mazur, B., Deforming Galois representations , in Galois groups over Q (Berkeley, CA, 1987), Mathematical Sciences Research Institute Publications, vol. 16 (Springer, New York, 1989), 385–437.CrossRefGoogle Scholar
Mazur, B., Deformation theory of Galois representations , in Modular forms and galois representations, eds Cornell, G., Silverman, J. H. and Stevens, G. (Springer, New York, 1997).Google Scholar
Neukirch, J., Schmidt, A. and Wingberg, K., Cohomology of number fields, Grundlehren der Mathematischen Wissenschaften (Fundamental Principles of Mathematical Sciences), vol. 323, second edition (Springer, Berlin, 2008).CrossRefGoogle Scholar
Quillen, D., On the cohomology and K-theory of the general linear groups over a finite field , Ann. of Math. (2) 96 (1972), 552–586.CrossRefGoogle Scholar
Rainone, R., On the inverse problem for deformation rings of representations. Master’s thesis, Universiteit Leiden (2010). http://www.math.leidenuniv.nl/en/theses/205/.Google Scholar
Rosenberg, J., Algebraic K-theory and its applications, Graduate Texts in Mathematics, vol. 147 (Springer, New York, 1994).CrossRefGoogle Scholar
Sah, C.-H., Cohomology of split group extensions , J. Algebra 29 (1974), 255–302.CrossRefGoogle Scholar
Sah, C.-H., Cohomology of split group extensions, II , J. Algebra 45 (1977), 17–68.CrossRefGoogle Scholar
Serre, J.-P., Abelian l-adic representations and elliptic curves, Research Notes in Mathematics, vol. 7 (A. K. Peters, Wellesley, MA, 1998); with the collaboration of Willem Kuyk and John Labute, revised reprint of the 1968 original.Google Scholar
Srinivas, V., Algebraic K theory, Modern Birkhäuser Classics, reprint of the 1996 second edition (Birkhäuser, Boston, 2008).Google Scholar
Wilson, R. et al. , Atlas of finite group representations. http://brauer.maths.qmul.ac.uk/Atlas/v3/matrep/2A8G1-Z4r4aB0.Google Scholar