Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-25T08:09:50.914Z Has data issue: false hasContentIssue false
  • English
  • Français

Instantons and Bar-Natan homology

Part of: Graph theory Differential topology

Published online by Cambridge University Press:  22 March 2021

P. B. Kronheimer  and
T. S. Mrowka
P. B. Kronheimer
Affiliation:
Department of Mathematics, Harvard University, 1 Oxford Street, Cambridge, MA02138, [email protected]
T. S. Mrowka
Affiliation:
Department of Mathematics, MIT, 77 Massachusetts Avenue, Cambridge, MA02139, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A spectral sequence is established whose 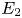$E_{2}$ page is Bar-Natan's variant of Khovanov homology and which abuts to a deformation of instanton homology for knots and links. This spectral sequence arises as a specialization of a spectral sequence whose 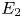$E_{2}$ page is a characteristic-2 version of 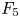$F_{5}$ homology in Khovanov's classification.

Keywords

instantonsKhovanov homologyBar-Natan homologyknotsspectral sequence

MSC classification

Primary: 57R58: Floer homology
Secondary: 05C15: Coloring of graphs and hypergraphs
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 3 , March 2021 , pp. 484 - 528
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The work of the first author was supported by the National Science Foundation through NSF grants DMS-1405652 and DMS-1707924. The work of the second author was supported by NSF grants DMS-1406348 and DMS-1808794, and by a grant from the Simons Foundation, grant number 503559 TSM.

References

Alishahi, A., Unknotting number and Khovanov homology, Pacific J. Math. 301 (2019), 15–29.10.2140/pjm.2019.301.15CrossRefGoogle Scholar
Alishahi, A. and Eftekhary, E., Knot Floer homology and the unknotting number, Geom. Topol. 24 (2020), 2435–2469.10.2140/gt.2020.24.2435CrossRefGoogle Scholar
Bar-Natan, D., Khovanov's homology for tangles and cobordisms, Geom. Topol. 9 (2005), 1443–1499.10.2140/gt.2005.9.1443CrossRefGoogle Scholar
Fintushel, R. and Stern, R. J., $\textrm {SO}(3)$-connections and the topology of $4$-manifolds, J. Differential Geom. 20 (1984), 523–539.10.4310/jdg/1214439293CrossRefGoogle Scholar
Khovanov, M., A categorification of the Jones polynomial, Duke Math. J. 101 (2000), 359–426.10.1215/S0012-7094-00-10131-7CrossRefGoogle Scholar
Khovanov, M., Link homology and Frobenius extensions, Fund. Math. 190 (2006), 179–190.10.4064/fm190-0-6CrossRefGoogle Scholar
Kronheimer, P. B., An obstruction to removing intersection points in immersed surfaces, Topology 36 (1997), 931–962.10.1016/S0040-9383(96)00020-1CrossRefGoogle Scholar
Kronheimer, P. B. and Mrowka, T. S., Embedded surfaces and the structure of Donaldson's polynomial invariants, J. Differential Geom. 41 (1995), 573–734.10.4310/jdg/1214456482CrossRefGoogle Scholar
Kronheimer, P. B. and Mrowka, T. S., Knot homology groups from instantons, J. Topol. 4 (2011), 835–918.10.1112/jtopol/jtr024CrossRefGoogle Scholar
Kronheimer, P. B. and Mrowka, T. S., Khovanov homology is an unknot-detector, Publ. Math. Inst. Hautes Études Sci. 113 (2012), 97–208.10.1007/s10240-010-0030-yCrossRefGoogle Scholar
Kronheimer, P. B. and Mrowka, T. S., Gauge theory and Rasmussen's invariant, J. Topol. 6 (2013), 659–674.10.1112/jtopol/jtt008CrossRefGoogle Scholar
Kronheimer, P. B. and Mrowka, T. S., A deformation of instanton homology for webs, Geom. Topol. 23 (2019), 1491–1547.10.2140/gt.2019.23.1491CrossRefGoogle Scholar
Kronheimer, P. B. and Mrowka, T. S., Tait colorings, and an instanton homology for webs and foams, J. Eur. Math. Soc. (JEMS) 21 (2019), 55–119.10.4171/JEMS/831CrossRefGoogle Scholar
Kronheimer, P. B. and Mrowka, T. S., Instantons and some concordance invariants of knots, J. Lond. Math. Soc., to appear. Preprint (2019), arXiv:1910.11129.Google Scholar
Lee, E. S., A new structure on Khovanov's homology, PhD thesis, Massachusetts Institute of Technology (ProQuest LLC, Ann Arbor, MI, 2003).Google Scholar
Lee, E. S., An endomorphism of the Khovanov invariant, Adv. Math. 197 (2005), 554–586.10.1016/j.aim.2004.10.015CrossRefGoogle Scholar
Lin, F., Bar-Natan's deformation of Khovanov homology and involutive monopole Floer homology, Math. Ann. 373 (2019), 489–516.10.1007/s00208-018-1675-yCrossRefGoogle Scholar
Ozsváth, P. S., Stipsicz, A. I. and Szabó, Z., Grid homology for knots and links, Mathematical Surveys and Monographs, vol. 208 (American Mathematical Society, Providence, RI, 2015).10.1090/surv/208CrossRefGoogle Scholar
Rasmussen, J., Khovanov homology and the slice genus, Invent. Math. 182 (2010), 419–447.10.1007/s00222-010-0275-6CrossRefGoogle Scholar
Xie, Y., On the framed singular instanton Floer homology from higher rank bundles, PhD thesis, Harvard University (ProQuest LLC, Ann Arbor, MI, 2016).Google Scholar