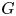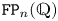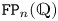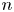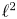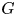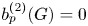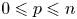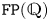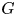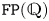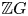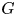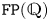1. Introduction
A group ![]() $G$ is algebraically fibred (or simply fibred) if it admits a homomorphism onto
$G$ is algebraically fibred (or simply fibred) if it admits a homomorphism onto ![]() $\mathbb {Z}$ with a finitely generated kernel. The interest in algebraic fibrings arose from the study of
$\mathbb {Z}$ with a finitely generated kernel. The interest in algebraic fibrings arose from the study of ![]() $3$-manifolds fibring over the circle. Using the long exact sequence of homotopy groups associated to a fibration, one sees that a surface bundle
$3$-manifolds fibring over the circle. Using the long exact sequence of homotopy groups associated to a fibration, one sees that a surface bundle ![]() $M \rightarrow S^1$, where
$M \rightarrow S^1$, where ![]() $M$ is a compact
$M$ is a compact ![]() $3$-manifold, induces an algebraic fibration
$3$-manifold, induces an algebraic fibration ![]() $\pi _1(M) \rightarrow \mathbb {Z}$. A celebrated theorem of Stallings [Reference StallingsSta62] establishes the converse: if
$\pi _1(M) \rightarrow \mathbb {Z}$. A celebrated theorem of Stallings [Reference StallingsSta62] establishes the converse: if ![]() $G$ is isomorphic to the fundamental group of a closed, compact
$G$ is isomorphic to the fundamental group of a closed, compact ![]() $3$-manifold
$3$-manifold ![]() $M$, then an algebraic fibration
$M$, then an algebraic fibration ![]() $G \rightarrow \mathbb {Z}$ is induced by a surface bundle
$G \rightarrow \mathbb {Z}$ is induced by a surface bundle ![]() $M \rightarrow S^1$.
$M \rightarrow S^1$.
Recently, Kielak characterised the virtual algebraic fibring of residually finite rationally solvable (RFRS) groups in terms of the vanishing of the first ![]() $\ell ^2$-Betti number. More precisely, he showed the following.
$\ell ^2$-Betti number. More precisely, he showed the following.
Theorem 1.1 (Kielak [Reference KielakKie20c])
Let ![]() $G$ be an infinite finitely generated virtually RFRS group. Then
$G$ be an infinite finitely generated virtually RFRS group. Then ![]() $G$ virtually algebraically fibres if and only if
$G$ virtually algebraically fibres if and only if ![]() $b_1^{(2)}(G) = 0$.
$b_1^{(2)}(G) = 0$.
Virtually RFRS groups arise naturally in geometric group theory; for example, subgroups of right-angled Artin groups and right-angled Coxeter groups are virtually RFRS and, in particular, special groups (in the sense of Haglund and Wise) are RFRS. Moreover, the RFRS property passes to subgroups and is preserved by taking products and free products of RFRS groups. Kielak's theorem is an algebraic analogue of the following theorem of Agol, which was a key step in confirming Thurston's virtually fibred conjecture.
Theorem 1.2 (Agol [Reference AgolAgo08])
Every compact and irreducible ![]() $3$-manifold
$3$-manifold ![]() $M$ with
$M$ with ![]() $\chi (M) = 0$ and nontrivial RFRS fundamental group admits a finite covering that fibres over the circle.
$\chi (M) = 0$ and nontrivial RFRS fundamental group admits a finite covering that fibres over the circle.
Since algebraic fibrings induce topological fibrings of ![]() $3$-manifolds, Kielak's theorem generalises the above theorem of Agol by removing the assumption that
$3$-manifolds, Kielak's theorem generalises the above theorem of Agol by removing the assumption that ![]() $G$ is the fundamental group of a
$G$ is the fundamental group of a ![]() $3$-manifold. Note that [Reference LückLüc02, Theorem 4.1] states that if
$3$-manifold. Note that [Reference LückLüc02, Theorem 4.1] states that if ![]() $M$ is a compact, irreducible
$M$ is a compact, irreducible ![]() $3$-manifold with no
$3$-manifold with no ![]() $S^2$ boundary components, then
$S^2$ boundary components, then ![]() $b_1^{(2)}(\pi _1(M)) = -\chi (M)$. Thus, we interpret the condition
$b_1^{(2)}(\pi _1(M)) = -\chi (M)$. Thus, we interpret the condition ![]() $b_1^{(2)}(G) = 0$ in Kielak's theorem as the algebraic analogue of the condition
$b_1^{(2)}(G) = 0$ in Kielak's theorem as the algebraic analogue of the condition ![]() $\chi (M) = 0$ in Agol's theorem.
$\chi (M) = 0$ in Agol's theorem.
In light of Kielak's theorem, it is natural to ask whether the vanishing of higher ![]() $\ell ^2$-Betti numbers of a group
$\ell ^2$-Betti numbers of a group ![]() $G$ controls the higher finiteness properties of the kernel of the virtual fibration. Indeed, Kielak conjectured that a virtually RFRS group of type
$G$ controls the higher finiteness properties of the kernel of the virtual fibration. Indeed, Kielak conjectured that a virtually RFRS group of type ![]() $\mathtt {FP}_n(\mathbb {Q})$ virtually algebraically fibres with kernel of type
$\mathtt {FP}_n(\mathbb {Q})$ virtually algebraically fibres with kernel of type ![]() $\mathtt {FP}_n(\mathbb {Q})$ if and only if
$\mathtt {FP}_n(\mathbb {Q})$ if and only if ![]() $b_p^{(2)}(G)$ vanishes for all
$b_p^{(2)}(G)$ vanishes for all ![]() $p \leqslant n$ (see [Reference KielakKie20b, Conjecture 8]). The main result of this paper confirms Kielak's conjecture, and gives another characterisation of RFRS groups virtually fibring with kernel of type
$p \leqslant n$ (see [Reference KielakKie20b, Conjecture 8]). The main result of this paper confirms Kielak's conjecture, and gives another characterisation of RFRS groups virtually fibring with kernel of type ![]() $\mathtt {FP}_n(\mathbb {Q})$. We also note that the equivalence of parts (2) and (3) in the following theorem generalises [Reference Jaikin-ZapirainJZ21, Corollary 1.5], where Jaikin-Zapirain proved the
$\mathtt {FP}_n(\mathbb {Q})$. We also note that the equivalence of parts (2) and (3) in the following theorem generalises [Reference Jaikin-ZapirainJZ21, Corollary 1.5], where Jaikin-Zapirain proved the ![]() $n = 1$ case.
$n = 1$ case.
Theorem A Let ![]() $G$ be a virtually RFRS group of type
$G$ be a virtually RFRS group of type ![]() $\mathtt {FP}_n(\mathbb {Q})$. Then the following are equivalent:
$\mathtt {FP}_n(\mathbb {Q})$. Then the following are equivalent:
(1)
 $b_p^{(2)}(G) = 0$ for all
$b_p^{(2)}(G) = 0$ for all  $p \leqslant n$;
$p \leqslant n$;(2) there is a finite-index subgroup
 $H \leqslant G$ and a surjection
$H \leqslant G$ and a surjection  $\varphi \colon H \rightarrow \mathbb {Z}$ such that
$\varphi \colon H \rightarrow \mathbb {Z}$ such that  $\ker \varphi$ is of type
$\ker \varphi$ is of type  $\mathtt {FP}_n(\mathbb {Q})$;
$\mathtt {FP}_n(\mathbb {Q})$;(3) there is a finite-index subgroup
 $H' \!\leqslant\! G$ and a surjection
$H' \!\leqslant\! G$ and a surjection  $\varphi ' \colon H' \!\rightarrow\! \mathbb {Z}$ such that
$\varphi ' \colon H' \!\rightarrow\! \mathbb {Z}$ such that  $b_p(\ker \varphi ') < \infty$ for all
$b_p(\ker \varphi ') < \infty$ for all  $p \leqslant n$.
$p \leqslant n$.
It should be emphasised that if ![]() $\ker \varphi '$ has finite Betti numbers in dimensions
$\ker \varphi '$ has finite Betti numbers in dimensions ![]() $\leqslant n$, it is not necessarily the case that
$\leqslant n$, it is not necessarily the case that ![]() $\ker \varphi '$ is of type
$\ker \varphi '$ is of type ![]() $\mathtt {FP}_n(\mathbb {Q})$. We prove a more general theorem that treats algebraic fibring with kernels of type
$\mathtt {FP}_n(\mathbb {Q})$. We prove a more general theorem that treats algebraic fibring with kernels of type ![]() $\mathtt {FP}_n(\mathbb {F})$ for any skew-field
$\mathtt {FP}_n(\mathbb {F})$ for any skew-field ![]() $\mathbb {F}$, from which we obtain Theorem A as a special case. Before stating the result, we give some background. If
$\mathbb {F}$, from which we obtain Theorem A as a special case. Before stating the result, we give some background. If ![]() $\mathbb {F}$ is a skew-field and
$\mathbb {F}$ is a skew-field and ![]() $G$ is a locally indicable group, then under certain conditions the group ring
$G$ is a locally indicable group, then under certain conditions the group ring ![]() $\mathbb {F}G$ embeds into a skew-field
$\mathbb {F}G$ embeds into a skew-field ![]() $\mathcal {D}_{\mathbb {F}G}$ called the Hughes-free division ring of
$\mathcal {D}_{\mathbb {F}G}$ called the Hughes-free division ring of ![]() $\mathbb {F}G$ (see Definition 2.3). If it exists,
$\mathbb {F}G$ (see Definition 2.3). If it exists, ![]() $\mathcal {D}_{\mathbb {F}G}$ is unique up to
$\mathcal {D}_{\mathbb {F}G}$ is unique up to ![]() $\mathbb {F}G$-algebra isomorphism [Reference HughesHug70] and the
$\mathbb {F}G$-algebra isomorphism [Reference HughesHug70] and the ![]() $\mathcal {D}_{\mathbb {F}G}$-homology of
$\mathcal {D}_{\mathbb {F}G}$-homology of ![]() $G$ in dimension
$G$ in dimension ![]() $p$ is defined to be
$p$ is defined to be ![]() $H_p^{\mathcal {D}_{\mathbb {F}{G}}}(G) := H_p(G; \mathcal {D}_{\mathbb {F}{G}})$. The
$H_p^{\mathcal {D}_{\mathbb {F}{G}}}(G) := H_p(G; \mathcal {D}_{\mathbb {F}{G}})$. The ![]() $p$th
$p$th ![]() $\mathcal {D}_{\mathbb {F}G}$-Betti number is defined to be
$\mathcal {D}_{\mathbb {F}G}$-Betti number is defined to be
In [Reference Jaikin-ZapirainJZ21, Corollary 1.3], Jaikin-Zapirain proved that if ![]() $G$ is finitely generated and RFRS, then
$G$ is finitely generated and RFRS, then ![]() $\mathcal {D}_{\mathbb {F}G}$ exists for any skew-field
$\mathcal {D}_{\mathbb {F}G}$ exists for any skew-field ![]() $\mathbb {F}$ and, if
$\mathbb {F}$ and, if ![]() $\mathbb {F} = \mathbb {Q}$, it is isomorphic to the Linnell skew-field of
$\mathbb {F} = \mathbb {Q}$, it is isomorphic to the Linnell skew-field of ![]() $G$. For the purposes of this paper, it will not be necessary to know how the Linnell skew-field is defined, but that it can be used to define the
$G$. For the purposes of this paper, it will not be necessary to know how the Linnell skew-field is defined, but that it can be used to define the ![]() $\ell ^2$-homology and
$\ell ^2$-homology and ![]() $\ell ^2$-Betti numbers of a group
$\ell ^2$-Betti numbers of a group ![]() $G$ (see Definition 6.9). Importantly for us, when
$G$ (see Definition 6.9). Importantly for us, when ![]() $G$ is finitely generated and RFRS, we have
$G$ is finitely generated and RFRS, we have ![]() $b_p^{\mathcal {D}_{\mathbb {Q} G}} (G) = b_p^{(2)}(G)$ for all
$b_p^{\mathcal {D}_{\mathbb {Q} G}} (G) = b_p^{(2)}(G)$ for all ![]() $p$. We prove the following theorem, which reduces to Theorem A in the case
$p$. We prove the following theorem, which reduces to Theorem A in the case ![]() $\mathbb {F} = \mathbb {Q}$.
$\mathbb {F} = \mathbb {Q}$.
Theorem B Let ![]() $\mathbb {F}$ be a skew-field and let
$\mathbb {F}$ be a skew-field and let ![]() $G$ be a virtually RFRS group of type
$G$ be a virtually RFRS group of type ![]() $\mathtt {FP}_n(\mathbb {F})$. Then the following are equivalent:
$\mathtt {FP}_n(\mathbb {F})$. Then the following are equivalent:
(1)
 $b_p^{\mathcal {D}_{\mathbb {F}{G}}} = 0$ for all
$b_p^{\mathcal {D}_{\mathbb {F}{G}}} = 0$ for all  $p \leqslant n$;
$p \leqslant n$;(2) there is a finite-index subgroup
 $H \leqslant G$ and a surjection
$H \leqslant G$ and a surjection  $\varphi \colon H \rightarrow \mathbb {Z}$ such that
$\varphi \colon H \rightarrow \mathbb {Z}$ such that  $\ker \varphi$ is of type
$\ker \varphi$ is of type  $\mathtt {FP}_n(\mathbb {F})$;
$\mathtt {FP}_n(\mathbb {F})$;(3) there is a finite-index subgroup
 $H' \leqslant G$ and a surjection
$H' \leqslant G$ and a surjection  $\varphi ' \colon H' \rightarrow \mathbb {Z}$ such that
$\varphi ' \colon H' \rightarrow \mathbb {Z}$ such that  $b_p(\ker \varphi '; \mathbb {F}) < \infty$ for all
$b_p(\ker \varphi '; \mathbb {F}) < \infty$ for all  $p \leqslant n$.
$p \leqslant n$.
We highlight the following corollary, which implies, in particular, that if ![]() $\mathbb {F}$ and
$\mathbb {F}$ and ![]() $\mathbb {F}'$ are skew-fields of the same characteristic, then a RFRS group
$\mathbb {F}'$ are skew-fields of the same characteristic, then a RFRS group ![]() $G$ is
$G$ is ![]() $\mathcal {D}_{\mathbb {F}{G}}$-acyclic in dimensions
$\mathcal {D}_{\mathbb {F}{G}}$-acyclic in dimensions ![]() $\leqslant n$ if and only if it is
$\leqslant n$ if and only if it is ![]() $\mathcal {D}_{\mathbb {F}'G}$-acyclic in dimensions
$\mathcal {D}_{\mathbb {F}'G}$-acyclic in dimensions ![]() $\leqslant n$. Moreover, it also implies that if
$\leqslant n$. Moreover, it also implies that if ![]() $G$ is
$G$ is ![]() $\mathcal {D}_{\mathbb {F}_p G}$ acyclic in dimensions
$\mathcal {D}_{\mathbb {F}_p G}$ acyclic in dimensions ![]() $\leqslant n$ for some prime
$\leqslant n$ for some prime ![]() $p$, then it is also
$p$, then it is also ![]() $\ell ^2$-acyclic in dimensions
$\ell ^2$-acyclic in dimensions ![]() $\leqslant n$.
$\leqslant n$.
Corollary C (Corollary 6.15)
Let ![]() $G$ be a virtually RFRS group and let
$G$ be a virtually RFRS group and let ![]() $n \in \mathbb {N}$.
$n \in \mathbb {N}$.
(1) If
 $\mathbb {F}$ and
$\mathbb {F}$ and  $\mathbb {F}'$ are skew-fields of the same characteristic, then
$\mathbb {F}'$ are skew-fields of the same characteristic, then  $G$ virtually algebraically fibres with kernel of type
$G$ virtually algebraically fibres with kernel of type  $\mathtt {FP}_n(\mathbb {F})$ if and only if it virtually algebraically fibres with kernel of type
$\mathtt {FP}_n(\mathbb {F})$ if and only if it virtually algebraically fibres with kernel of type  $\mathtt {FP}_n(\mathbb {F}')$.
$\mathtt {FP}_n(\mathbb {F}')$.(2) If
 $p$ is a prime such that
$p$ is a prime such that  $G$ virtually algebraically fibres with kernel of type
$G$ virtually algebraically fibres with kernel of type  $\mathtt {FP}_n(\mathbb {F}_p)$, then it virtually fibres with kernel of type
$\mathtt {FP}_n(\mathbb {F}_p)$, then it virtually fibres with kernel of type  $\mathtt {FP}_n(\mathbb {Q})$.
$\mathtt {FP}_n(\mathbb {Q})$.
The final section of the paper is devoted to some applications of the main theorems. An interesting question is to determine general conditions under which amenable groups are elementary amenable. There are many examples of amenable groups that are not elementary amenable, for instance, Grigorchuk's group of intermediate growth, but it is not known whether there are examples of amenable groups of finite cohomological dimension that are not elementary amenable. Moreover, elementary amenable groups of finite cohomological dimension are virtually solvable by [Reference HillmanHil91, Lemma 2] and [Reference Hillman and LinnellHL92, Corollary 1]. This leads us to the following question, which first appeared in the work of Degrijse.
Question 1.3 (Degrijse [Reference DegrijseDeg16])
Are amenable groups of finite cohomological dimension over ![]() $\mathbb {Z}$ virtually solvable?
$\mathbb {Z}$ virtually solvable?
We obtain the following as an application of Theorem A, which provides evidence of a positive answer for virtually RFRS groups.
Theorem D (Theorem 7.4)
If ![]() $G$ is a virtually (amenable RFRS group of type
$G$ is a virtually (amenable RFRS group of type ![]() $\mathtt {FP}(\mathbb {Q})$), then
$\mathtt {FP}(\mathbb {Q})$), then ![]() $G$ is virtually Abelian.
$G$ is virtually Abelian.
We think of this result as being in the same vein as the well-known fact that nilpotent RFRS groups must be virtually Abelian (see, e.g., [Reference Koberda and SuciuKS20, Proposition 2.5]). As a corollary, we confirm the following conjecture of Baer for virtually RFRS groups of type ![]() $\mathtt {FP}(\mathbb {Q})$. Note that this class of groups includes all virtually compact special groups.
$\mathtt {FP}(\mathbb {Q})$. Note that this class of groups includes all virtually compact special groups.
Conjecture 1.4 If ![]() $G$ is a group such that the group ring
$G$ is a group such that the group ring ![]() $\mathbb {Z} G$ is Noetherian, then
$\mathbb {Z} G$ is Noetherian, then ![]() $G$ is polycyclic-by-finite.
$G$ is polycyclic-by-finite.
Hall showed that polycyclic-by-finite groups have Noetherian group rings [Reference HallHal59, Theorem 4], but it is still unknown whether the converse holds. Some progress was made recently by Kropholler and Lorensen, who showed that if ![]() $RG$ is right Noetherian and
$RG$ is right Noetherian and ![]() $R$ is a domain, then
$R$ is a domain, then ![]() $G$ is amenable and all of its subgroups are finitely generated [Reference Kropholler and LorensenKL19, Corollary B]. This result provides evidence for the conjecture, as the only known amenable groups in which every subgroup is finitely generated are polycyclic-by-finite. We obtain the following as a consequence of Theorem D and Kielak's appendix to [Reference BartholdiBar19].
$G$ is amenable and all of its subgroups are finitely generated [Reference Kropholler and LorensenKL19, Corollary B]. This result provides evidence for the conjecture, as the only known amenable groups in which every subgroup is finitely generated are polycyclic-by-finite. We obtain the following as a consequence of Theorem D and Kielak's appendix to [Reference BartholdiBar19].
Corollary E (Corollary 7.6)
Let ![]() $G$ be a virtually RFRS group of type
$G$ be a virtually RFRS group of type ![]() $\mathtt {FP}(\mathbb {Q})$ such that
$\mathtt {FP}(\mathbb {Q})$ such that ![]() $\mathbb {Z} G$ is Noetherian. Then
$\mathbb {Z} G$ is Noetherian. Then ![]() $G$ is virtually Abelian.
$G$ is virtually Abelian.
Finally, we mention that Llosa-Isenrich, Martelli and Py remarked in [Reference Llosa Isenrich, Martelli and PyLMP21] that an easy consequence of Theorem A, Agol's theorem [Reference AgolAgo13], and the work of Agol and Bergeron, Haglund and Wise [Reference Bergeron, Haglund and WiseBHW11] is the existence of hyperbolic groups containing type ![]() $\mathtt {FP}_{n-1}(\mathbb {Q})$ subgroups that are not of type
$\mathtt {FP}_{n-1}(\mathbb {Q})$ subgroups that are not of type ![]() $\mathtt {FP}_n(\mathbb {Q})$ for all
$\mathtt {FP}_n(\mathbb {Q})$ for all ![]() $n \in \mathbb {N}$. We also remark that, by the same argument, such lattices in
$n \in \mathbb {N}$. We also remark that, by the same argument, such lattices in ![]() $\mathrm {PO}(2n+1,1)$ algebraically fibre with kernel of type
$\mathrm {PO}(2n+1,1)$ algebraically fibre with kernel of type ![]() $\mathtt {FP}(\mathbb {Q})$.
$\mathtt {FP}(\mathbb {Q})$.
Proposition 1.5 [Reference Llosa Isenrich, Martelli and PyLMP21, Proposition 19]
Let ![]() $\Gamma \in \mathrm {PO}(m,1)$ be a hyperbolic arithmetic lattice of the simplest type. If
$\Gamma \in \mathrm {PO}(m,1)$ be a hyperbolic arithmetic lattice of the simplest type. If ![]() $m = 2n$, then
$m = 2n$, then ![]() $\Gamma$ virtually fibres with kernel of type
$\Gamma$ virtually fibres with kernel of type ![]() $\mathtt {FP}_{n-1}(\mathbb {Q})$ but not of type
$\mathtt {FP}_{n-1}(\mathbb {Q})$ but not of type ![]() $\mathtt {FP}_n(\mathbb {Q})$. If
$\mathtt {FP}_n(\mathbb {Q})$. If ![]() $m = 2n+1$, then
$m = 2n+1$, then ![]() $\Gamma$ virtually fibres with kernel of type
$\Gamma$ virtually fibres with kernel of type ![]() $\mathtt {FP}(\mathbb {Q})$.
$\mathtt {FP}(\mathbb {Q})$.
Our methods do not allow us to say anything about algebraic fibring with kernels of type ![]() $\mathtt {FP}_n(\mathbb {F}_p)$ for
$\mathtt {FP}_n(\mathbb {F}_p)$ for ![]() $p$ prime (nor about algebraic fibring with stronger finiteness properties of the kernel) since the
$p$ prime (nor about algebraic fibring with stronger finiteness properties of the kernel) since the ![]() $\mathcal {D}_{\mathbb {F}_p G}$-Betti numbers of simplest type hyperbolic arithmetic lattices are not known to vanish. In a subsequent paper [Reference Llosa Isenrich and PyLP24], Llosa-Isenrich and Py showed that there are hyperbolic arithmetic lattices of the simplest type in
$\mathcal {D}_{\mathbb {F}_p G}$-Betti numbers of simplest type hyperbolic arithmetic lattices are not known to vanish. In a subsequent paper [Reference Llosa Isenrich and PyLP24], Llosa-Isenrich and Py showed that there are hyperbolic arithmetic lattices of the simplest type in ![]() $\mathrm {PU}(n,1)$ that virtually fibre with kernel of type
$\mathrm {PU}(n,1)$ that virtually fibre with kernel of type ![]() $\mathtt {F}_{n-1}$ but not of type
$\mathtt {F}_{n-1}$ but not of type ![]() $\mathtt {FP}_n(\mathbb {Q})$, answering a question of Brady about the existence of subgroups of hyperbolic groups with exotic finiteness properties.
$\mathtt {FP}_n(\mathbb {Q})$, answering a question of Brady about the existence of subgroups of hyperbolic groups with exotic finiteness properties.
1.1 Structure of the paper
In § 2 we introduce some of the main tools and objects that will be used throughout the paper. In particular, we define finiteness properties of groups, Hughes-free division rings, RFRS groups and Ore localisation.
Section 3 recalls what we will need from the theory of valuations on free resolutions developed by Bieri and Renz in [Reference Bieri and RenzBR88]. The results in [Reference Bieri and RenzBR88] are stated for free resolutions over group rings with coefficients in ![]() $\mathbb {Z}$, however we will need them for coefficients in an arbitrary associative, unital ring
$\mathbb {Z}$, however we will need them for coefficients in an arbitrary associative, unital ring ![]() $R$. There is no essential dependence on the ring, so our proofs are similar to those of Bieri and Renz after replacing
$R$. There is no essential dependence on the ring, so our proofs are similar to those of Bieri and Renz after replacing ![]() $\mathbb {Z}$ with
$\mathbb {Z}$ with ![]() $R$.
$R$.
In § 4, we introduce the complex of horochains associated to a free resolution equipped with a valuation.
Section 5 begins with the definition of the higher ![]() $\Sigma$-invariants
$\Sigma$-invariants ![]() $\Sigma _R^n(G; M)$ for a group
$\Sigma _R^n(G; M)$ for a group ![]() $G$, a unital, associative ring
$G$, a unital, associative ring ![]() $R$, and an
$R$, and an ![]() $RG$-module
$RG$-module ![]() $M$. Again, these were introduced in the case
$M$. Again, these were introduced in the case ![]() $R = \mathbb {Z}$ in [Reference Bieri and RenzBR88], and reduce to the usual Bieri–Neumann–Strebel (BNS) invariant when
$R = \mathbb {Z}$ in [Reference Bieri and RenzBR88], and reduce to the usual Bieri–Neumann–Strebel (BNS) invariant when ![]() $n = 1$,
$n = 1$, ![]() $R = \mathbb {Z}$ and
$R = \mathbb {Z}$ and ![]() $M = \mathbb {Z}$ is the trivial
$M = \mathbb {Z}$ is the trivial ![]() $\mathbb {Z} G$-module. The rest of the section is devoted to the proof of Theorem 5.3, which gives equivalent characterisations of the invariants
$\mathbb {Z} G$-module. The rest of the section is devoted to the proof of Theorem 5.3, which gives equivalent characterisations of the invariants ![]() $\Sigma _R^n(G; M)$. The most important characterisation for our purposes is the following:
$\Sigma _R^n(G; M)$. The most important characterisation for our purposes is the following: ![]() $[\chi ] \in \Sigma _R^n(G;M)$ if and only if
$[\chi ] \in \Sigma _R^n(G;M)$ if and only if ![]() $\operatorname {Tor}_i^{RG}(\widehat {RG}^\chi, M) = 0$ for all
$\operatorname {Tor}_i^{RG}(\widehat {RG}^\chi, M) = 0$ for all ![]() $i \leqslant n$, where
$i \leqslant n$, where ![]() $\widehat {RG}^\chi$ is the Novikov ring. When
$\widehat {RG}^\chi$ is the Novikov ring. When ![]() $n = 1$, this result is Sikorav's theorem [Reference SikoravSik87] and is a key ingredient in Kielak's proof of Theorem 1.1. The proof follows arguments given in [Reference Bieri and RenzBR88] and Schweitzer's appendix to [Reference BieriBie07]. Theorem 5.3 is the main technical result that will be used in the proof of Theorem 6.7.
$n = 1$, this result is Sikorav's theorem [Reference SikoravSik87] and is a key ingredient in Kielak's proof of Theorem 1.1. The proof follows arguments given in [Reference Bieri and RenzBR88] and Schweitzer's appendix to [Reference BieriBie07]. Theorem 5.3 is the main technical result that will be used in the proof of Theorem 6.7.
In § 6 we introduce ![]() $\mathcal {D}_{\mathbb {F}G}$-homology and prove properties of
$\mathcal {D}_{\mathbb {F}G}$-homology and prove properties of ![]() $\mathcal {D}_{\mathbb {F}G}$-Betti numbers analogous to those of
$\mathcal {D}_{\mathbb {F}G}$-Betti numbers analogous to those of ![]() $\ell ^2$-Betti numbers. Namely, we prove that
$\ell ^2$-Betti numbers. Namely, we prove that
(Lemma 6.3) whenever ![]() $\mathcal {D}_{\mathbb {F}G}$ exists and
$\mathcal {D}_{\mathbb {F}G}$ exists and ![]() $H$ is a finite index subgroup of
$H$ is a finite index subgroup of ![]() $G$. In Theorem 6.4, we show that if
$G$. In Theorem 6.4, we show that if ![]() $b_p^{\mathcal {D}_{\mathbb {F}K}}(K) < \infty$ and
$b_p^{\mathcal {D}_{\mathbb {F}K}}(K) < \infty$ and ![]() $G$ fits into a short exact sequence
$G$ fits into a short exact sequence ![]() $1 \rightarrow K \rightarrow G \rightarrow \mathbb {Z} \rightarrow 1$, then
$1 \rightarrow K \rightarrow G \rightarrow \mathbb {Z} \rightarrow 1$, then ![]() $b_p^{\mathcal {D}_{\mathbb {F}G}}(G) = 0$. This should be thought of as an analogue of [Reference LückLüc02, Theorem 7.2] for
$b_p^{\mathcal {D}_{\mathbb {F}G}}(G) = 0$. This should be thought of as an analogue of [Reference LückLüc02, Theorem 7.2] for ![]() $\mathcal {D}_{\mathbb {F}G}$-Betti numbers. We then prove the main result, Theorem 6.7, and obtain Theorem 6.11 as a special case. In Theorem 6.14, we show that virtually fibring with kernel of type
$\mathcal {D}_{\mathbb {F}G}$-Betti numbers. We then prove the main result, Theorem 6.7, and obtain Theorem 6.11 as a special case. In Theorem 6.14, we show that virtually fibring with kernel of type ![]() $\mathtt {FP}_n(\mathbb {Q})$ is equivalent to having a virtual map to
$\mathtt {FP}_n(\mathbb {Q})$ is equivalent to having a virtual map to ![]() $\mathbb {Z}$ whose kernel has finite Betti numbers in dimensions
$\mathbb {Z}$ whose kernel has finite Betti numbers in dimensions ![]() $\leqslant n$.
$\leqslant n$.
We conclude with the proofs of Theorem 7.4 and Corollary 7.6 in § 7, and mention related work of Llosa-Isenrich, Martelli, and Py.
2. Preliminaries
Remark In the following, all rings will be associative and unital with ![]() $1 \neq 0$.
$1 \neq 0$.
2.1 Finiteness properties
Definition 2.1 (Type  $\mathtt {FP}_n$)
$\mathtt {FP}_n$)
Let ![]() $R$ be a ring and
$R$ be a ring and ![]() $M$ be a left
$M$ be a left ![]() $R$-module. We say that
$R$-module. We say that ![]() $M$ is of type
$M$ is of type ![]() $\mathtt {FP}_n$, and write
$\mathtt {FP}_n$, and write ![]() $M \in \mathtt {FP}_n$, if
$M \in \mathtt {FP}_n$, if ![]() $M$ has a projective resolution
$M$ has a projective resolution
by left ![]() $R$-modules, where
$R$-modules, where ![]() $P_j$ is finitely generated for
$P_j$ is finitely generated for ![]() $j \leqslant n$. If we want to specify the ring, we say that
$j \leqslant n$. If we want to specify the ring, we say that ![]() $M$ is of type
$M$ is of type ![]() $\mathtt {FP}_n$ over
$\mathtt {FP}_n$ over ![]() $R$ and write
$R$ and write ![]() $M \in \mathtt {FP}_n(R)$. If
$M \in \mathtt {FP}_n(R)$. If ![]() $P_j = 0$ for
$P_j = 0$ for ![]() $j > n$, then we write
$j > n$, then we write ![]() $M \in \mathtt {FP}(R)$.
$M \in \mathtt {FP}(R)$.
A group ![]() $G$ is of type
$G$ is of type ![]() $\mathtt {FP}_n$ over
$\mathtt {FP}_n$ over ![]() $R$ if the trivial
$R$ if the trivial ![]() $RG$-module
$RG$-module ![]() $R$ is of type
$R$ is of type ![]() $\mathtt {FP}_n(RG)$; in this case, we write
$\mathtt {FP}_n(RG)$; in this case, we write ![]() $G \in \mathtt {FP}_n(R)$. Similarly, if the trivial
$G \in \mathtt {FP}_n(R)$. Similarly, if the trivial ![]() $RG$-module
$RG$-module ![]() $R$ is of type
$R$ is of type ![]() $\mathtt {FP}(RG)$, then we write
$\mathtt {FP}(RG)$, then we write ![]() $G \in \mathtt {FP}(R)$.
$G \in \mathtt {FP}(R)$.
We will often use the fact that an ![]() $R$-module
$R$-module ![]() $M$ is of type
$M$ is of type ![]() $\mathtt {FP}_n$ if and only if there is a free resolution
$\mathtt {FP}_n$ if and only if there is a free resolution ![]() $\cdots \rightarrow F_{n+1} \rightarrow F_n \rightarrow \cdots \rightarrow F_0 \rightarrow M \rightarrow 0$ with
$\cdots \rightarrow F_{n+1} \rightarrow F_n \rightarrow \cdots \rightarrow F_0 \rightarrow M \rightarrow 0$ with ![]() $F_j$ finitely generated for
$F_j$ finitely generated for ![]() $j \leqslant n$ (see [Reference BrownBro94, Proposition VIII.4.3]). Note that the analogous fact does not hold for type
$j \leqslant n$ (see [Reference BrownBro94, Proposition VIII.4.3]). Note that the analogous fact does not hold for type ![]() $\mathtt {FP}$.
$\mathtt {FP}$.
The following definition will not be needed until § 7.
Definition 2.2 (cohomological dimension)
A resolution ![]() $\cdots \rightarrow P_1 \rightarrow P_0 \rightarrow M \rightarrow 0$ of an
$\cdots \rightarrow P_1 \rightarrow P_0 \rightarrow M \rightarrow 0$ of an ![]() $R$-module
$R$-module ![]() $M$ has length
$M$ has length ![]() $n$ if
$n$ if ![]() $P_n \neq 0$ and
$P_n \neq 0$ and ![]() $P_m = 0$ for
$P_m = 0$ for ![]() $m > n$. A group
$m > n$. A group ![]() $G$ has cohomological dimension
$G$ has cohomological dimension ![]() $n$ over
$n$ over ![]() $R$ if
$R$ if ![]() $n$ is the shortest length of any projective resolution of the trivial
$n$ is the shortest length of any projective resolution of the trivial ![]() $RG$-module
$RG$-module ![]() $R$. In this case we will write
$R$. In this case we will write ![]() $\operatorname {cd}_R (G) = n$. If
$\operatorname {cd}_R (G) = n$. If ![]() $R$ has no finite-length projective resolution, then
$R$ has no finite-length projective resolution, then ![]() $\operatorname {cd}_R(G) = \infty$.
$\operatorname {cd}_R(G) = \infty$.
Note that ![]() $G \in \mathtt {FP}(R)$ implies that
$G \in \mathtt {FP}(R)$ implies that ![]() $G$ has finite cohomological dimension over
$G$ has finite cohomological dimension over ![]() $R$, but not conversely.
$R$, but not conversely.
2.2 Hughes-free division rings
We are following Jaikin-Zapirain's exposition of this material; in particular, Definitions 2.3 and 2.4 are taken from [Reference Jaikin-ZapirainJZ21].
Definition 2.3 (Hughes-free division rings)
Let ![]() $\mathbb {F}$ and
$\mathbb {F}$ and ![]() $\mathcal {D}$ be skew-fields, let
$\mathcal {D}$ be skew-fields, let ![]() $G$ be a locally indicable group, and let
$G$ be a locally indicable group, and let ![]() $\varphi \colon \mathbb {F} G \rightarrow \mathcal {D}$ be a ring homomorphism. Then the pair
$\varphi \colon \mathbb {F} G \rightarrow \mathcal {D}$ be a ring homomorphism. Then the pair ![]() $(\mathcal {D}, \varphi )$ is Hughes-free if:
$(\mathcal {D}, \varphi )$ is Hughes-free if:
(1)
 $\mathcal {D}$ is the skew-field generated by
$\mathcal {D}$ is the skew-field generated by  $\varphi (\mathbb {F} G)$, i.e. if
$\varphi (\mathbb {F} G)$, i.e. if  $\mathcal {E} \subseteq \mathcal {D}$ is a skew-field such that
$\mathcal {E} \subseteq \mathcal {D}$ is a skew-field such that  $\varphi (\mathbb {F} G) \subseteq \mathcal {E}$, then
$\varphi (\mathbb {F} G) \subseteq \mathcal {E}$, then  $\mathcal {E} = \mathcal {D}$;
$\mathcal {E} = \mathcal {D}$;(2) for every nontrivial finitely generated subgroup
 $H \leqslant G$, every normal subgroup
$H \leqslant G$, every normal subgroup  $N \triangleleft H$ such that
$N \triangleleft H$ such that  $H/N \cong \mathbb {Z}$, and every set of elements
$H/N \cong \mathbb {Z}$, and every set of elements  $h_1, \ldots, h_n \in H$ lying in pairwise distinct cosets of
$h_1, \ldots, h_n \in H$ lying in pairwise distinct cosets of  $N$, the sum
is direct, where
$N$, the sum
is direct, where \[ \langle\varphi(\mathbb{F}N)\rangle \cdot \varphi(h_1) + \cdots + \langle\varphi(\mathbb{F}N)\rangle \cdot \varphi(h_n) \]
\[ \langle\varphi(\mathbb{F}N)\rangle \cdot \varphi(h_1) + \cdots + \langle\varphi(\mathbb{F}N)\rangle \cdot \varphi(h_n) \]
 $\langle \varphi (\mathbb {F}N)\rangle$ is the sub-skew-field of
$\langle \varphi (\mathbb {F}N)\rangle$ is the sub-skew-field of  $\mathcal {D}$ generated by
$\mathcal {D}$ generated by  $\varphi (\mathbb {F}N)$.
$\varphi (\mathbb {F}N)$.
Hughes showed that if such a pair ![]() $(\mathcal {D},\varphi )$ exists, then
$(\mathcal {D},\varphi )$ exists, then ![]() $\mathcal {D}$ is unique up to
$\mathcal {D}$ is unique up to ![]() $\mathbb {F}G$-algebra isomorphism [Reference HughesHug70]. Thus, we denote
$\mathbb {F}G$-algebra isomorphism [Reference HughesHug70]. Thus, we denote ![]() $\mathcal {D}$ by
$\mathcal {D}$ by ![]() $\mathcal {D}_{\mathbb {F}G}$. Let
$\mathcal {D}_{\mathbb {F}G}$. Let ![]() $H \leqslant G$ be a subgroup and suppose that
$H \leqslant G$ be a subgroup and suppose that ![]() $\mathcal {D}_{\mathbb {F}G}$ exists. Then
$\mathcal {D}_{\mathbb {F}G}$ exists. Then ![]() $\mathcal {D}_{\mathbb {F}H}$ exists as well and is equal to
$\mathcal {D}_{\mathbb {F}H}$ exists as well and is equal to ![]() $\langle \varphi (\mathbb {F}H) \rangle \subseteq \mathcal {D}_{\mathbb {F}G}$. Hence, we will view
$\langle \varphi (\mathbb {F}H) \rangle \subseteq \mathcal {D}_{\mathbb {F}G}$. Hence, we will view ![]() $\mathcal {D}_{\mathbb {F}H}$ as a subset of
$\mathcal {D}_{\mathbb {F}H}$ as a subset of ![]() $\mathcal {D}_{\mathbb {F}G}$ whenever
$\mathcal {D}_{\mathbb {F}G}$ whenever ![]() $H$ is a subgroup of
$H$ is a subgroup of ![]() $G$. Moreover, Gräter showed that
$G$. Moreover, Gräter showed that ![]() $\mathcal {D}_{\mathbb {F}G}$ is strongly Hughes-free whenever it exists [Reference GräterGrä20, Corollary 8.3], which is to say that condition (2) above can be replaced with the following:
$\mathcal {D}_{\mathbb {F}G}$ is strongly Hughes-free whenever it exists [Reference GräterGrä20, Corollary 8.3], which is to say that condition (2) above can be replaced with the following:
(2′) for every nontrivial subgroup
 $H \leqslant G$, every normal subgroup
$H \leqslant G$, every normal subgroup  $N \triangleleft H$, and every set of elements
$N \triangleleft H$, and every set of elements  $h_1, \ldots, h_n \in H$ lying in pairwise distinct cosets of
$h_1, \ldots, h_n \in H$ lying in pairwise distinct cosets of  $N$, the sum
is direct.
$N$, the sum
is direct. \[ \langle\varphi(\mathbb{F}N)\rangle \cdot \varphi(h_1) + \cdots + \langle\varphi(\mathbb{F}N)\rangle \cdot \varphi(h_n) \]
\[ \langle\varphi(\mathbb{F}N)\rangle \cdot \varphi(h_1) + \cdots + \langle\varphi(\mathbb{F}N)\rangle \cdot \varphi(h_n) \]
Definition 2.4 (Crossed products)
A ring ![]() $R$ is
$R$ is ![]() $G$-graded if its underlying Abelian group is isomorphic to a direct sum
$G$-graded if its underlying Abelian group is isomorphic to a direct sum ![]() $\bigoplus _{g \in G} R_g$ of Abelian groups
$\bigoplus _{g \in G} R_g$ of Abelian groups ![]() $R_g$ and
$R_g$ and ![]() $R_g R_h \subseteq R_{gh}$ for all
$R_g R_h \subseteq R_{gh}$ for all ![]() $g,h \in G$. If
$g,h \in G$. If ![]() $R_g$ contains a unit for each
$R_g$ contains a unit for each ![]() $g \in G$, then we say that
$g \in G$, then we say that ![]() $R$ is a crossed product of
$R$ is a crossed product of ![]() $R_e$ and
$R_e$ and ![]() $G$, and we write
$G$, and we write ![]() $R = R_e * G$.
$R = R_e * G$.
Strong Hughes-freeness implies the following useful properties, which are stated in [Reference Jaikin-ZapirainJZ21].
Proposition 2.5 Let ![]() $G$ be a locally indicable group such that
$G$ be a locally indicable group such that ![]() $\mathcal {D}_{\mathbb {F}G}$ exists, let
$\mathcal {D}_{\mathbb {F}G}$ exists, let ![]() $\varphi$ be as in Definition 2.3 and let
$\varphi$ be as in Definition 2.3 and let ![]() $N \triangleleft G$ be a normal subgroup. If
$N \triangleleft G$ be a normal subgroup. If ![]() $R$ is the subring of
$R$ is the subring of ![]() $\mathcal {D}_{\mathbb {F}G}$ generated by
$\mathcal {D}_{\mathbb {F}G}$ generated by ![]() $\mathcal {D}_{\mathbb {F}N}$ and
$\mathcal {D}_{\mathbb {F}N}$ and ![]() $\varphi (\mathbb {F}G)$, then:
$\varphi (\mathbb {F}G)$, then:
(1)
 $R \cong \mathcal {D}_{\mathbb {F}N} * (G/N)$;
$R \cong \mathcal {D}_{\mathbb {F}N} * (G/N)$;(2) if
 $[G:N] < \infty$, then
$[G:N] < \infty$, then  $\mathcal {D}_{\mathbb {F}G} = R$.
$\mathcal {D}_{\mathbb {F}G} = R$.
Proof. Starting with property (1), let ![]() $\{t_i\}_{i \in I}$ be a transversal for
$\{t_i\}_{i \in I}$ be a transversal for ![]() $N$ in
$N$ in ![]() $G$. We claim that every element of
$G$. We claim that every element of ![]() $R$ can be written as a finite sum
$R$ can be written as a finite sum ![]() $\sum _i \alpha _i \varphi (t_i)$, where
$\sum _i \alpha _i \varphi (t_i)$, where ![]() $\alpha _i \in \mathcal {D}_{\mathbb {F}N}$ for each
$\alpha _i \in \mathcal {D}_{\mathbb {F}N}$ for each ![]() $i \in I$. This will conclude the proof of property (1) by strong Hughes-freeness. Since every element of
$i \in I$. This will conclude the proof of property (1) by strong Hughes-freeness. Since every element of ![]() $G$ is of the form
$G$ is of the form ![]() $n t_i$ for some
$n t_i$ for some ![]() $n \in N$ and
$n \in N$ and ![]() $i \in I$, it is enough to show that
$i \in I$, it is enough to show that ![]() $\varphi (t_i) a \varphi (t_i)^{-1} \in \mathcal {D}_{\mathbb {F} N}$ for every
$\varphi (t_i) a \varphi (t_i)^{-1} \in \mathcal {D}_{\mathbb {F} N}$ for every ![]() $i \in I$ and every
$i \in I$ and every ![]() $a \in \mathcal {D}_{\mathbb {F} N}$. Note that
$a \in \mathcal {D}_{\mathbb {F} N}$. Note that ![]() $\mathcal {D}_{\mathbb {F} N} = \bigcup _{j\geqslant 0} \mathcal {D}_j$ where
$\mathcal {D}_{\mathbb {F} N} = \bigcup _{j\geqslant 0} \mathcal {D}_j$ where ![]() $\mathcal {D}_0 = \varphi (\mathbb {F}N)$ and
$\mathcal {D}_0 = \varphi (\mathbb {F}N)$ and ![]() $\mathcal {D}_{j+1}$ is generated by
$\mathcal {D}_{j+1}$ is generated by ![]() $\mathcal {D}_j$ and the set
$\mathcal {D}_j$ and the set ![]() $\{x^{-1} : x \in \mathcal {D}_j \smallsetminus \{0\}\}$. Because
$\{x^{-1} : x \in \mathcal {D}_j \smallsetminus \{0\}\}$. Because ![]() $N$ is normal in
$N$ is normal in ![]() $G$, it is clear that
$G$, it is clear that ![]() $\varphi (\mathbb {F}N)$ is closed under conjugation by
$\varphi (\mathbb {F}N)$ is closed under conjugation by ![]() $\varphi (G)$. By induction, we see that each
$\varphi (G)$. By induction, we see that each ![]() $\mathcal {D}_j$ is closed under conjugation by
$\mathcal {D}_j$ is closed under conjugation by ![]() $\varphi (G)$.
$\varphi (G)$.
To prove property (2), we recall the fact that a finite-dimensional algebra over a skew-field with no zero-divisors is a skew-field. Hence, if ![]() $[G:N] < \infty$, then
$[G:N] < \infty$, then ![]() $R \cong \mathcal {D}_{\mathbb {F}N} * (G/N)$ is finite-dimensional over
$R \cong \mathcal {D}_{\mathbb {F}N} * (G/N)$ is finite-dimensional over ![]() $\mathcal {D}_{\mathbb {F}N}$ and is therefore a skew-field. However,
$\mathcal {D}_{\mathbb {F}N}$ and is therefore a skew-field. However, ![]() $\mathcal {D}_{\mathbb {F}G}$ is the smallest skew-field containing
$\mathcal {D}_{\mathbb {F}G}$ is the smallest skew-field containing ![]() $\varphi (\mathbb {F}G)$, so
$\varphi (\mathbb {F}G)$, so ![]() $\mathcal {D}_{\mathbb {F}G} = R$.
$\mathcal {D}_{\mathbb {F}G} = R$.
2.3 RFRS groups
RFRS groups were defined by Agol in [Reference AgolAgo08] in order to show that certain hyperbolic ![]() $3$-manifolds virtually fibre over the circle. Let
$3$-manifolds virtually fibre over the circle. Let ![]() $G$ be a group and let
$G$ be a group and let ![]() $G^\mathsf {ab} := G/[G,G]$ be its Abelianisation. Since
$G^\mathsf {ab} := G/[G,G]$ be its Abelianisation. Since ![]() $G^\mathsf {ab}$ is Abelian, it is canonically a
$G^\mathsf {ab}$ is Abelian, it is canonically a ![]() $\mathbb {Z}$-module, so we can form the tensor product
$\mathbb {Z}$-module, so we can form the tensor product ![]() $\mathbb {Q} \otimes _\mathbb {Z} G^\mathsf {ab}$, and there is a group homomorphism
$\mathbb {Q} \otimes _\mathbb {Z} G^\mathsf {ab}$, and there is a group homomorphism ![]() $G \rightarrow \mathbb {Q} \otimes _\mathbb {Z} G^{\mathsf {ab}}$ sending
$G \rightarrow \mathbb {Q} \otimes _\mathbb {Z} G^{\mathsf {ab}}$ sending ![]() $g \in G$ to
$g \in G$ to ![]() $1 \otimes g[G,G]$.
$1 \otimes g[G,G]$.
Definition 2.6 A group ![]() $G$ is RFRS if:
$G$ is RFRS if:
(1) there is a chain
 $G = G_0 \geqslant G_1 \geqslant G_2 \geqslant \cdots$ of finite index normal subgroups of
$G = G_0 \geqslant G_1 \geqslant G_2 \geqslant \cdots$ of finite index normal subgroups of  $G$ such that
$G$ such that  $\bigcap _{i=0}^\infty G_i = \{1\}$;
$\bigcap _{i=0}^\infty G_i = \{1\}$;(2)
 $\ker (G_i \rightarrow \mathbb {Q} \otimes _\mathbb {Z} G_i^{\mathsf {ab}}) \leqslant G_{i+1}$ for every
$\ker (G_i \rightarrow \mathbb {Q} \otimes _\mathbb {Z} G_i^{\mathsf {ab}}) \leqslant G_{i+1}$ for every  $i \geqslant 0$.
$i \geqslant 0$.
The following fact that will be used in the proof of Theorem 6.7.
Proposition 2.7 Let ![]() $G$ be a finitely generated RFRS group. Then:
$G$ be a finitely generated RFRS group. Then:
(1)
 $G$ is residually poly-
$G$ is residually poly- $\mathbb {Z}$;
$\mathbb {Z}$;(2)
 $G$ virtually retracts onto all of its finitely generated Abelian subgroups;
$G$ virtually retracts onto all of its finitely generated Abelian subgroups;(3)
 $G$ is locally indicable.
$G$ is locally indicable.
Proof. Item (1) is proven in [Reference Jaikin-ZapirainJZ21, Proposition 4.4]. We now prove item (2). By [Reference MinasyanMin21, Proposition 1.5], it suffices to show that ![]() $G$ virtually retracts onto its cyclic subgroups. Let
$G$ virtually retracts onto its cyclic subgroups. Let ![]() $G = G_0 \geqslant G_1 \geqslant \cdots$ be a RFRS chain and let
$G = G_0 \geqslant G_1 \geqslant \cdots$ be a RFRS chain and let ![]() $\langle a \rangle$ be a cyclic subgroup of
$\langle a \rangle$ be a cyclic subgroup of ![]() $G$. Let
$G$. Let ![]() $i$ be the unique integer such that
$i$ be the unique integer such that ![]() $a \in G_i \smallsetminus G_{i+1}$. It follows that
$a \in G_i \smallsetminus G_{i+1}$. It follows that ![]() $a$ is not in the kernel of the free Abelianisation map
$a$ is not in the kernel of the free Abelianisation map ![]() $G_i \rightarrow G_i^{\mathsf {fab}}$. Let
$G_i \rightarrow G_i^{\mathsf {fab}}$. Let ![]() $\overline {a}$ denote the image of
$\overline {a}$ denote the image of ![]() $a$ in
$a$ in ![]() $G_i^\mathsf {fab}$. There is a finite index subgroup
$G_i^\mathsf {fab}$. There is a finite index subgroup ![]() $H' \leqslant G_i^\mathsf {fab}$ and a retraction
$H' \leqslant G_i^\mathsf {fab}$ and a retraction ![]() $H' \rightarrow \langle \overline {a} \rangle$. Let
$H' \rightarrow \langle \overline {a} \rangle$. Let ![]() $H \leqslant G_i$ be the preimage of
$H \leqslant G_i$ be the preimage of ![]() $H'$. The composition
$H'$. The composition ![]() $H \rightarrow H' \rightarrow \langle \overline {a} \rangle \rightarrow \langle a \rangle$ is the desired retraction. Item (3) is an immediate consequence of item (1).
$H \rightarrow H' \rightarrow \langle \overline {a} \rangle \rightarrow \langle a \rangle$ is the desired retraction. Item (3) is an immediate consequence of item (1).
2.4 Ore localisation
Ore localisation is an analogue of usual localisation for noncommutative rings. Let ![]() $R$ be a ring and let
$R$ be a ring and let ![]() $S$ be its set of non-zero-divisors. Then
$S$ be its set of non-zero-divisors. Then ![]() $R$ satisfies the Ore condition if for every
$R$ satisfies the Ore condition if for every ![]() $r \in R$ and
$r \in R$ and ![]() $s \in S$ there are elements
$s \in S$ there are elements ![]() $p,p' \in R$ and
$p,p' \in R$ and ![]() $q,q' \in S$ such that
$q,q' \in S$ such that
If ![]() $S = R \setminus \{0\}$ and
$S = R \setminus \{0\}$ and ![]() $R$ satisfies the Ore condition, then it is called an Ore domain, and we can form its Ore localisation
$R$ satisfies the Ore condition, then it is called an Ore domain, and we can form its Ore localisation ![]() $\operatorname {Ore}(R)$ as follows. Define an equivalence relation
$\operatorname {Ore}(R)$ as follows. Define an equivalence relation ![]() $\sim _R$ on
$\sim _R$ on ![]() $R \times S$ by declaring that
$R \times S$ by declaring that ![]() $(r,s) \sim _R (r',s')$ if and only if there are elements
$(r,s) \sim _R (r',s')$ if and only if there are elements ![]() $a,b \in S$ such that
$a,b \in S$ such that
The equivalence class of ![]() $(r,s)$ under
$(r,s)$ under ![]() $\sim _R$ is denoted
$\sim _R$ is denoted ![]() $r/s$ and called a right fraction. Then
$r/s$ and called a right fraction. Then ![]() $\operatorname {Ore}(R)$ is defined to be the set of right fractions. We can similarly define an equivalence relation
$\operatorname {Ore}(R)$ is defined to be the set of right fractions. We can similarly define an equivalence relation ![]() $\sim _L$ and define
$\sim _L$ and define ![]() $\operatorname {Ore}(R)$ as a set of left fractions. The Ore condition ensures that these two constructions are isomorphic and indicates how to convert right fractions into left fractions and vice versa. For a detailed construction of
$\operatorname {Ore}(R)$ as a set of left fractions. The Ore condition ensures that these two constructions are isomorphic and indicates how to convert right fractions into left fractions and vice versa. For a detailed construction of ![]() $\operatorname {Ore}(R)$ and the definition of addition and multiplication making this set into a ring, we refer the reader to § 4.4 of Passman's book [Reference PassmanPas77].
$\operatorname {Ore}(R)$ and the definition of addition and multiplication making this set into a ring, we refer the reader to § 4.4 of Passman's book [Reference PassmanPas77].
The facts about Ore localisation that we will use are summarised in the following proposition.
Proposition 2.8 Let ![]() $R$ be an Ore domain. Then:
$R$ be an Ore domain. Then:
(1)
 $\operatorname {Ore}(R)$ is a skew-field;
$\operatorname {Ore}(R)$ is a skew-field;(2) for every
 $r \in R$, we have
$r \in R$, we have  $r / 1 = 1 \backslash r$ and the map
$r / 1 = 1 \backslash r$ and the map  $R \rightarrow \operatorname {Ore}(R), r \mapsto r/1 = 1 \backslash r$ is an injective ring homomorphism;
$R \rightarrow \operatorname {Ore}(R), r \mapsto r/1 = 1 \backslash r$ is an injective ring homomorphism;(3) (see [Reference Jaikin-ZapirainJZ21, Proposition 2.2(2)]) if
 $G$ is a group and
$G$ is a group and  $\mathbb {F}$ is a skew-field such that
$\mathbb {F}$ is a skew-field such that  $\mathcal {D}_{\mathbb {F}G}$ exists and
$\mathcal {D}_{\mathbb {F}G}$ exists and  $K$ is a normal subgroup such that
$K$ is a normal subgroup such that  $G / K \cong \mathbb {Z}$, then
$G / K \cong \mathbb {Z}$, then  $\mathcal {D}_{\mathbb {F}G} \cong \operatorname {Ore}(\mathcal {D}_{\mathbb {F}K} * (G/K))$.
$\mathcal {D}_{\mathbb {F}G} \cong \operatorname {Ore}(\mathcal {D}_{\mathbb {F}K} * (G/K))$.
3. Valuations on free resolutions
In this section, we introduce valuations on free resolutions over a group ring. We very closely follow Bieri and Renz [Reference Bieri and RenzBR88] where the theory is developed in the case where the ring is ![]() $\mathbb {Z}$. Their proofs go through without change when
$\mathbb {Z}$. Their proofs go through without change when ![]() $\mathbb {Z}$ is replaced by an arbitrary ring
$\mathbb {Z}$ is replaced by an arbitrary ring ![]() $R$.
$R$.
Let ![]() $R$ be a ring,
$R$ be a ring, ![]() $G$ a group, and
$G$ a group, and ![]() $M$ a left
$M$ a left ![]() $RG$-module. A free resolution of
$RG$-module. A free resolution of ![]() $M$ is an exact sequence
$M$ is an exact sequence
of left ![]() $RG$-modules, where
$RG$-modules, where ![]() $F_i$ is free for all
$F_i$ is free for all ![]() $i \geqslant 0$. We will usually omit the subscripts on the boundary maps
$i \geqslant 0$. We will usually omit the subscripts on the boundary maps ![]() $\partial _n$ and denote the free resolution by
$\partial _n$ and denote the free resolution by ![]() $F_\bullet \rightarrow M \rightarrow 0$. Let
$F_\bullet \rightarrow M \rightarrow 0$. Let ![]() $F$ be the free
$F$ be the free ![]() $RG$-module
$RG$-module ![]() $\bigoplus _{i = 0}^\infty F_i$, and define the
$\bigoplus _{i = 0}^\infty F_i$, and define the ![]() $n$-skeleton of
$n$-skeleton of ![]() $F$ to be
$F$ to be ![]() $F^{(n)} := \bigoplus _{i = 0}^n F_i$. The elements of
$F^{(n)} := \bigoplus _{i = 0}^n F_i$. The elements of ![]() $F$ are called chains, so a chain is not necessarily an element of
$F$ are called chains, so a chain is not necessarily an element of ![]() $F_i$ for any
$F_i$ for any ![]() $i$ in our context. Fixing a basis
$i$ in our context. Fixing a basis ![]() $X_i$ for each
$X_i$ for each ![]() $F_i$, we note that
$F_i$, we note that ![]() $X := \bigcup _{i=0}^\infty X_i$ is a basis for
$X := \bigcup _{i=0}^\infty X_i$ is a basis for ![]() $F$ and
$F$ and ![]() $X^{(n)} := \bigcup _{i = 0}^n X_i$ is a basis for
$X^{(n)} := \bigcup _{i = 0}^n X_i$ is a basis for ![]() $F^{(n)}$. The resolution
$F^{(n)}$. The resolution ![]() $F_\bullet \rightarrow M \rightarrow 0$ is admissible with respect to
$F_\bullet \rightarrow M \rightarrow 0$ is admissible with respect to ![]() $X$ if
$X$ if ![]() $\partial x \neq 0$ for every
$\partial x \neq 0$ for every ![]() $x \in X$. We will always assume that our free resolutions are admissible with respect to the basis we are working with. This is not a strong requirement, since if all boundary maps are nonzero, then
$x \in X$. We will always assume that our free resolutions are admissible with respect to the basis we are working with. This is not a strong requirement, since if all boundary maps are nonzero, then ![]() $F$ has a basis with respect to which
$F$ has a basis with respect to which ![]() $F_\bullet \rightarrow M \rightarrow 0$ is admissible; otherwise, we can truncate the resolution and choose a basis to obtain an admissible resolution of finite length. We also define the support of a chain
$F_\bullet \rightarrow M \rightarrow 0$ is admissible; otherwise, we can truncate the resolution and choose a basis to obtain an admissible resolution of finite length. We also define the support of a chain ![]() $c \in F$ (with respect to
$c \in F$ (with respect to ![]() $X$), denoted
$X$), denoted ![]() $\operatorname {supp}_X(c)$, as follows: every chain
$\operatorname {supp}_X(c)$, as follows: every chain ![]() $c \in F$ can be written uniquely as
$c \in F$ can be written uniquely as ![]() $\sum _{g\in G, x \in X} r_{g,x} gx$, where
$\sum _{g\in G, x \in X} r_{g,x} gx$, where ![]() $r_{g,x} \in R$. Then
$r_{g,x} \in R$. Then ![]() $\operatorname {supp}_X (c) := \{ gx : r_{g,x} \neq 0 \}$; we will usually drop the subscript
$\operatorname {supp}_X (c) := \{ gx : r_{g,x} \neq 0 \}$; we will usually drop the subscript ![]() $X$ when the basis is understood.
$X$ when the basis is understood.
Let ![]() $\chi \colon G \rightarrow \mathbb {R}$ be a nontrivial character, that is, a nonzero group homomorphism from
$\chi \colon G \rightarrow \mathbb {R}$ be a nontrivial character, that is, a nonzero group homomorphism from ![]() $G$ to the additive group
$G$ to the additive group ![]() $\mathbb {R}$. This provides the elements of
$\mathbb {R}$. This provides the elements of ![]() $G$ with a notion of height, which we now extend to the chains of
$G$ with a notion of height, which we now extend to the chains of ![]() $F$. Let
$F$. Let ![]() $\mathbb {R}_\infty = \mathbb {R} \cup \{\infty \}$, where
$\mathbb {R}_\infty = \mathbb {R} \cup \{\infty \}$, where ![]() $\infty$ is an element such that
$\infty$ is an element such that ![]() $t < \infty$ for every
$t < \infty$ for every ![]() $t \in \mathbb {R}$. We construct a function
$t \in \mathbb {R}$. We construct a function ![]() $v_X \colon F \rightarrow \mathbb {R}_{\infty }$ via the following inductive procedure. For an element
$v_X \colon F \rightarrow \mathbb {R}_{\infty }$ via the following inductive procedure. For an element ![]() $c \in F_0$, define
$c \in F_0$, define ![]() $v_X(c) = \inf \{ \chi (g) : gx \in \operatorname {supp}(c) \}$. Let
$v_X(c) = \inf \{ \chi (g) : gx \in \operatorname {supp}(c) \}$. Let ![]() $n > 0$ and assume that we have defined
$n > 0$ and assume that we have defined ![]() $v_X$ on
$v_X$ on ![]() $F_{n-1}$. For
$F_{n-1}$. For ![]() $x \in X_n$, let
$x \in X_n$, let ![]() $v_X(x) := v_X(\partial x)$. For
$v_X(x) := v_X(\partial x)$. For ![]() $c \in F_n$, set
$c \in F_n$, set ![]() $v_X(c) = \inf \{ \chi (g) + v_X(x) : gx \in \operatorname {supp}(c) \}$. For an arbitrary
$v_X(c) = \inf \{ \chi (g) + v_X(x) : gx \in \operatorname {supp}(c) \}$. For an arbitrary ![]() $c \in F$, write
$c \in F$, write ![]() $c = \sum _i c_i$, where
$c = \sum _i c_i$, where ![]() $c_i \in F_i$, and define
$c_i \in F_i$, and define ![]() $c = \inf _i\{ v_X(c_i) \}$. We are assuming the convention
$c = \inf _i\{ v_X(c_i) \}$. We are assuming the convention ![]() $v_X(0) = \infty$, since
$v_X(0) = \infty$, since ![]() $\operatorname {supp}(0) = \varnothing$. The function
$\operatorname {supp}(0) = \varnothing$. The function ![]() $v_X$ is called the valuation extending
$v_X$ is called the valuation extending ![]() $\chi$ with respect to
$\chi$ with respect to ![]() $X$. It is clear from the definition that
$X$. It is clear from the definition that ![]() $v_X(c) = \inf \{ \chi (g) + v_X(x) : gx \in \operatorname {supp}(c) \}$ for any chain
$v_X(c) = \inf \{ \chi (g) + v_X(x) : gx \in \operatorname {supp}(c) \}$ for any chain ![]() $c \in F$. Again, we will usually drop the
$c \in F$. Again, we will usually drop the ![]() $X$ in the subscript when the basis is understood.
$X$ in the subscript when the basis is understood.
Proposition 3.1 For the valuation ![]() $v_X = v \colon F \rightarrow \mathbb {R}_\infty$ defined above and for any
$v_X = v \colon F \rightarrow \mathbb {R}_\infty$ defined above and for any ![]() $c, c' \in F$ and
$c, c' \in F$ and ![]() $g \in G$, we have:
$g \in G$, we have:
(1)
 $v(c + c') \geqslant \min \{ v(c), v(c') \}$;
$v(c + c') \geqslant \min \{ v(c), v(c') \}$;(2)
 $v(c) \leqslant v(rc)$ for all
$v(c) \leqslant v(rc)$ for all  $r \in R$, and
$r \in R$, and  $v(c) = v(rc)$ if
$v(c) = v(rc)$ if  $r$ is not a zero-divisor;
$r$ is not a zero-divisor;(3) if
 $v(c) \neq v(c')$, then
$v(c) \neq v(c')$, then  $v(c + c') = \min \{ v(c), v(c') \}$;
$v(c + c') = \min \{ v(c), v(c') \}$;(4)
 $v(g c) = \chi (g) + v(c)$;
$v(g c) = \chi (g) + v(c)$;(5)
 $v(c) = \infty$ if and only if
$v(c) = \infty$ if and only if  $c = 0$;
$c = 0$;(6) if
 $c \in \bigoplus _{i \geqslant 1} F_i$, then
$c \in \bigoplus _{i \geqslant 1} F_i$, then  $v(\partial c) \geqslant v(c)$.
$v(\partial c) \geqslant v(c)$.
Proof. Property (1) follows from the fact that ![]() $\operatorname {supp}(c+c') \subseteq \operatorname {supp}(c) \cup \operatorname {supp}(c')$. The first part of property (2) follows from the fact that
$\operatorname {supp}(c+c') \subseteq \operatorname {supp}(c) \cup \operatorname {supp}(c')$. The first part of property (2) follows from the fact that ![]() $\operatorname {supp}(c) \supseteq \operatorname {supp}(rc)$. If
$\operatorname {supp}(c) \supseteq \operatorname {supp}(rc)$. If ![]() $r$ is not a zero-divisor, then
$r$ is not a zero-divisor, then ![]() $\operatorname {supp}(c) = \operatorname {supp}(rc)$, which yields the second statement of property (2).
$\operatorname {supp}(c) = \operatorname {supp}(rc)$, which yields the second statement of property (2).
To prove property (3), assume without loss of generality that ![]() $v(c) < v(c')$. Then,
$v(c) < v(c')$. Then,
Since we assumed that ![]() $v(c) < v(c')$, the previous line implies that
$v(c) < v(c')$, the previous line implies that ![]() $\min \{ v(c+c'), v(c') \} = v(c + c')$; hence,
$\min \{ v(c+c'), v(c') \} = v(c + c')$; hence, ![]() $v(c) = \min \{ v(c), v(c') \} \geqslant v(c + c')$. However,
$v(c) = \min \{ v(c), v(c') \} \geqslant v(c + c')$. However, ![]() $v(c + c') \geqslant \min \{v(c),v(c')\}$ by property (1), so we obtain property (3).
$v(c + c') \geqslant \min \{v(c),v(c')\}$ by property (1), so we obtain property (3).
For property (4), we have
 \begin{align*} v(gc) &= \inf\{ \chi(h) + v(x) : hx \in \operatorname{supp}(gc) \} \\ &= \inf\{ \chi(g (g^{-1} h)) + v(x) : hx \in g \cdot \operatorname{supp} c \} \\ &= \chi(g) + \inf\{ \chi(g^{-1} h) + v(x) : (g^{-1} h)x \in \operatorname{supp} c \} \\ &= \chi(g) + v(c). \end{align*}
\begin{align*} v(gc) &= \inf\{ \chi(h) + v(x) : hx \in \operatorname{supp}(gc) \} \\ &= \inf\{ \chi(g (g^{-1} h)) + v(x) : hx \in g \cdot \operatorname{supp} c \} \\ &= \chi(g) + \inf\{ \chi(g^{-1} h) + v(x) : (g^{-1} h)x \in \operatorname{supp} c \} \\ &= \chi(g) + v(c). \end{align*}
For property (5), we first show that if ![]() $c \in F_n \setminus \{0 \}$, then
$c \in F_n \setminus \{0 \}$, then ![]() $v(c) < \infty$ by induction on
$v(c) < \infty$ by induction on ![]() $n$. This is true for
$n$. This is true for ![]() $n = 0$ since
$n = 0$ since ![]() $\chi (G) \subseteq \mathbb {R}$. Now let
$\chi (G) \subseteq \mathbb {R}$. Now let ![]() $n > 0$. Since
$n > 0$. Since ![]() $c \neq 0$, there is some element
$c \neq 0$, there is some element ![]() $gx$ in its support, where
$gx$ in its support, where ![]() $g \in G$ and
$g \in G$ and ![]() $x \in X$. Then
$x \in X$. Then
by the inductive hypothesis and by admissibility of ![]() $F_\bullet \rightarrow M \rightarrow 0$ with respect to
$F_\bullet \rightarrow M \rightarrow 0$ with respect to ![]() $X$. For a general nonzero element
$X$. For a general nonzero element ![]() $c \in F$, write
$c \in F$, write ![]() $c = \sum _i c_i$ with
$c = \sum _i c_i$ with ![]() $c_i \in F_i$. Then
$c_i \in F_i$. Then ![]() $v(c) = \inf _i\{ v(c_i) \} < \infty$ since at least one of the chains
$v(c) = \inf _i\{ v(c_i) \} < \infty$ since at least one of the chains ![]() $c_i$ is nonzero. Conversely, if
$c_i$ is nonzero. Conversely, if ![]() $c = 0$, then
$c = 0$, then ![]() $v(c) = \infty$, since the infimum of the empty set is
$v(c) = \infty$, since the infimum of the empty set is ![]() $\infty$.
$\infty$.
For property (6), let ![]() $c = \sum _{g \in G, x \in X} r_{g,x} gx \in \bigoplus _{i \geqslant 1} F_i$. Then
$c = \sum _{g \in G, x \in X} r_{g,x} gx \in \bigoplus _{i \geqslant 1} F_i$. Then
 $$\begin{align*} v(\partial c) &= v\bigg(\partial\bigg(\sum_{g \in G, x \in X} r_{g,x} gx\bigg)\bigg) \\ &= v\bigg(\sum_{g \in G, x \in X} r_{g,x} g \partial x\bigg) \\ &\geqslant \inf\{ v(r_{g,x} g\partial x) : gx \in \operatorname{supp}(c)\} \\ &\geqslant \inf \{v( g\partial x) : gx \in \operatorname{supp}(c)\} \\ &= \inf\{ \chi(g) + v(\partial x) : gx \in \operatorname{supp}(c) \} \\ &= \inf\{ \chi(g) + v(x) : gx \in \operatorname{supp}(c) \} \\ &= v(c).\end{align*}$$
$$\begin{align*} v(\partial c) &= v\bigg(\partial\bigg(\sum_{g \in G, x \in X} r_{g,x} gx\bigg)\bigg) \\ &= v\bigg(\sum_{g \in G, x \in X} r_{g,x} g \partial x\bigg) \\ &\geqslant \inf\{ v(r_{g,x} g\partial x) : gx \in \operatorname{supp}(c)\} \\ &\geqslant \inf \{v( g\partial x) : gx \in \operatorname{supp}(c)\} \\ &= \inf\{ \chi(g) + v(\partial x) : gx \in \operatorname{supp}(c) \} \\ &= \inf\{ \chi(g) + v(x) : gx \in \operatorname{supp}(c) \} \\ &= v(c).\end{align*}$$Definition 3.2 (Valuation subcomplex and essential acyclicity)
Given an admissible free resolution ![]() $F_\bullet \rightarrow M \rightarrow 0$ over
$F_\bullet \rightarrow M \rightarrow 0$ over ![]() $RG$ (with respect to some fixed basis
$RG$ (with respect to some fixed basis ![]() $X$), a nontrivial character
$X$), a nontrivial character ![]() $\chi \colon G \rightarrow \mathbb {R}$, and the valuation
$\chi \colon G \rightarrow \mathbb {R}$, and the valuation ![]() $v \colon F \rightarrow \mathbb {R}_\infty$ extending
$v \colon F \rightarrow \mathbb {R}_\infty$ extending ![]() $\chi$, define the valuation subcomplex of
$\chi$, define the valuation subcomplex of ![]() $F$ with respect to
$F$ with respect to ![]() $v$ to be the chain complex
$v$ to be the chain complex ![]() $\cdots \rightarrow F_n^v \rightarrow \cdots \rightarrow F_0^v \rightarrow M \rightarrow 0$, where
$\cdots \rightarrow F_n^v \rightarrow \cdots \rightarrow F_0^v \rightarrow M \rightarrow 0$, where ![]() $F_n^v = \{c \in F_n : v(c) \geqslant 0\}$. We denote the valuation subcomplex by
$F_n^v = \{c \in F_n : v(c) \geqslant 0\}$. We denote the valuation subcomplex by ![]() $F_\bullet ^v \rightarrow M \rightarrow 0$ and let
$F_\bullet ^v \rightarrow M \rightarrow 0$ and let ![]() $F^v := \bigoplus _{i = 0}^\infty F_i^v$. Proposition 3.1(6) ensures that
$F^v := \bigoplus _{i = 0}^\infty F_i^v$. Proposition 3.1(6) ensures that ![]() $F_\bullet ^v \rightarrow M \rightarrow 0$ is a chain complex of left
$F_\bullet ^v \rightarrow M \rightarrow 0$ is a chain complex of left ![]() $RG_\chi$-modules, where
$RG_\chi$-modules, where ![]() $G_\chi$ is the monoid
$G_\chi$ is the monoid ![]() $\{g \in G : \chi (g) \geqslant 0\}$. It is not hard to show that each
$\{g \in G : \chi (g) \geqslant 0\}$. It is not hard to show that each ![]() $F_i^v$ is a free
$F_i^v$ is a free ![]() $RG_\chi$-module and has an
$RG_\chi$-module and has an ![]() $RG_\chi$-basis of cardinality
$RG_\chi$-basis of cardinality ![]() ${\vert X_i\vert }$, where
${\vert X_i\vert }$, where ![]() $X_i$ is an
$X_i$ is an ![]() $RG$-basis for
$RG$-basis for ![]() $F_i$.
$F_i$.
The chain complex ![]() $F_\bullet ^v \rightarrow M \rightarrow 0$ is essentially acyclic in dimension
$F_\bullet ^v \rightarrow M \rightarrow 0$ is essentially acyclic in dimension ![]() $n$ if there is a real number
$n$ if there is a real number ![]() $D \geqslant 0$ such that for every cycle
$D \geqslant 0$ such that for every cycle ![]() $z \in F_n^v$ there is a
$z \in F_n^v$ there is a ![]() $c \in F_{n+1}$ with
$c \in F_{n+1}$ with ![]() $\partial c = z$ and
$\partial c = z$ and ![]() $D \geqslant v(z) - v(c)$. We extend the definition of essential acyclicity to dimension
$D \geqslant v(z) - v(c)$. We extend the definition of essential acyclicity to dimension ![]() $-1$ by declaring that
$-1$ by declaring that ![]() $v(m) = 0$ for all
$v(m) = 0$ for all ![]() $m \in M \setminus \{0\}$.
$m \in M \setminus \{0\}$.
The definition of essential acyclicity in dimension ![]() $n$ is equivalent to the following seemingly weaker condition: for every cycle
$n$ is equivalent to the following seemingly weaker condition: for every cycle ![]() $z \in F_n^v$, there is a
$z \in F_n^v$, there is a ![]() $c \in F_{n+1}$ such that
$c \in F_{n+1}$ such that ![]() $\partial c = z$ and
$\partial c = z$ and ![]() $v(c) \geqslant -D$. To see this, let
$v(c) \geqslant -D$. To see this, let ![]() $z \in F_n^v$ be a cycle. It is easily shown that
$z \in F_n^v$ be a cycle. It is easily shown that ![]() $v(F) \subseteq \chi (G) \cup \{\infty \}$, so there is a
$v(F) \subseteq \chi (G) \cup \{\infty \}$, so there is a ![]() $g \in G$ such that
$g \in G$ such that ![]() $\chi (g) = v(z)$. Since
$\chi (g) = v(z)$. Since ![]() $g^{-1} z$ is also in
$g^{-1} z$ is also in ![]() $F_n^v$ with
$F_n^v$ with ![]() $v(g^{-1} z) = 0$, there is some
$v(g^{-1} z) = 0$, there is some ![]() $c \in F_{n+1}^v$ such that
$c \in F_{n+1}^v$ such that ![]() $\partial c = g^{-1} z$ and
$\partial c = g^{-1} z$ and ![]() $v(c) \geqslant -D$. Thus,
$v(c) \geqslant -D$. Thus, ![]() $\partial (gc) = z$, and
$\partial (gc) = z$, and ![]() $D \geqslant v(z) - v(gc)$.
$D \geqslant v(z) - v(gc)$.
4. Horochains
Definition 4.1 (Complex of horochains and horo-acyclicity)
Let ![]() $F_\bullet \rightarrow M \rightarrow 0$ be an admissible free resolution with respect to some basis
$F_\bullet \rightarrow M \rightarrow 0$ be an admissible free resolution with respect to some basis ![]() $X$, let
$X$, let ![]() $\chi \colon G \rightarrow \mathbb {R}$ be a nontrivial character, and let
$\chi \colon G \rightarrow \mathbb {R}$ be a nontrivial character, and let ![]() $v \colon F \rightarrow \mathbb {R}_\infty$ be the valuation extending
$v \colon F \rightarrow \mathbb {R}_\infty$ be the valuation extending ![]() $\chi$. Define
$\chi$. Define ![]() $\widehat {F}$ to be the left
$\widehat {F}$ to be the left ![]() $RG$-module of chains that are finitely supported below every height. More precisely,
$RG$-module of chains that are finitely supported below every height. More precisely, ![]() $\widehat {F}$ is the
$\widehat {F}$ is the ![]() $RG$-module of formal sums
$RG$-module of formal sums ![]() $\sum _{g \in G, x \in X} r_{g,x} g x$ such that
$\sum _{g \in G, x \in X} r_{g,x} g x$ such that ![]() $\{ gx : v(gx) \leqslant t, r_{g,x} \neq 0 \}$ is finite for every
$\{ gx : v(gx) \leqslant t, r_{g,x} \neq 0 \}$ is finite for every ![]() $t \in \mathbb {R}$. The elements of
$t \in \mathbb {R}$. The elements of ![]() $\widehat {F}$ are called horochains. If
$\widehat {F}$ are called horochains. If ![]() $\hat {c} \in \widehat {F}$, then its support is
$\hat {c} \in \widehat {F}$, then its support is ![]() $\operatorname {supp}_X(\hat {c}) := \{ gx : r_{g,x} \neq 0 \}$. Let
$\operatorname {supp}_X(\hat {c}) := \{ gx : r_{g,x} \neq 0 \}$. Let ![]() $\widehat {F}_i \subseteq \widehat {F}$ be the subset of chains with support in
$\widehat {F}_i \subseteq \widehat {F}$ be the subset of chains with support in ![]() $F_i$ and let
$F_i$ and let ![]() $\widehat {F}^{(n)} := \bigoplus _{i = 0}^n \widehat {F}_i$. Proposition 3.1(6) guarantees that
$\widehat {F}^{(n)} := \bigoplus _{i = 0}^n \widehat {F}_i$. Proposition 3.1(6) guarantees that ![]() $\partial \colon F_n \rightarrow F_{n-1}$ extends to a map
$\partial \colon F_n \rightarrow F_{n-1}$ extends to a map ![]() $\partial \colon \widehat {F}_n \rightarrow \widehat {F}_{n-1}$ in the obvious way, so we get a complex
$\partial \colon \widehat {F}_n \rightarrow \widehat {F}_{n-1}$ in the obvious way, so we get a complex ![]() $\cdots \rightarrow \widehat {F}_n \rightarrow \cdots \rightarrow \widehat {F}_0 \rightarrow 0$. Note that
$\cdots \rightarrow \widehat {F}_n \rightarrow \cdots \rightarrow \widehat {F}_0 \rightarrow 0$. Note that ![]() $\widehat {F}$ is not equal to
$\widehat {F}$ is not equal to ![]() $\bigoplus _{i = 0}^\infty \widehat {F}_i$ since the support of a horochain might intersect infinitely many of the modules
$\bigoplus _{i = 0}^\infty \widehat {F}_i$ since the support of a horochain might intersect infinitely many of the modules ![]() $\widehat {F}_i$. A cycle in the chain complex
$\widehat {F}_i$. A cycle in the chain complex ![]() $\widehat {F}$ is called a horocycle. We say that
$\widehat {F}$ is called a horocycle. We say that ![]() $F_\bullet \rightarrow M \rightarrow 0$ is horo-acyclic in dimensions
$F_\bullet \rightarrow M \rightarrow 0$ is horo-acyclic in dimensions ![]() $n \geqslant 0$ with respect to
$n \geqslant 0$ with respect to ![]() $v$ if the chain complex
$v$ if the chain complex ![]() $\cdots \rightarrow \widehat {F}_1 \rightarrow \widehat {F}_0 \rightarrow 0$ is acyclic in dimension
$\cdots \rightarrow \widehat {F}_1 \rightarrow \widehat {F}_0 \rightarrow 0$ is acyclic in dimension ![]() $n$.
$n$.
We can extend the definition of ![]() $v$ to
$v$ to ![]() $\widehat {F}$ by defining
$\widehat {F}$ by defining ![]() $v(\hat {c}) := \inf \{ v(gx) : \operatorname {supp}(\hat {c})\}$ for any horochain
$v(\hat {c}) := \inf \{ v(gx) : \operatorname {supp}(\hat {c})\}$ for any horochain ![]() $\hat {c}$. If
$\hat {c}$. If ![]() $\hat {c} \neq 0$, then
$\hat {c} \neq 0$, then ![]() $\{ v(gx) : \operatorname {supp}(\hat {c})\}$ is nonempty and attains a minimum because chains are finitely supported below any given height. Properties (1)–(5) of Proposition 3.1 hold in this setting with the same proofs.
$\{ v(gx) : \operatorname {supp}(\hat {c})\}$ is nonempty and attains a minimum because chains are finitely supported below any given height. Properties (1)–(5) of Proposition 3.1 hold in this setting with the same proofs.
A version of Proposition 3.1(6) holds for horochains, namely we have ![]() $v(\partial \hat {c}) \geqslant v(\hat {c})$ for all horochains
$v(\partial \hat {c}) \geqslant v(\hat {c})$ for all horochains ![]() $\hat {c}$, but we need to modify the proof: If
$\hat {c}$, but we need to modify the proof: If ![]() $\hat {c} = 0$, then the claim is clear. Otherwise, let
$\hat {c} = 0$, then the claim is clear. Otherwise, let ![]() $\hat {c} \neq 0$ be a horochain, and let
$\hat {c} \neq 0$ be a horochain, and let ![]() $gx \in \operatorname {supp}(\hat {c})$ be such that
$gx \in \operatorname {supp}(\hat {c})$ be such that ![]() $v(gx) = v(\hat {c})$. By the finite version of property (6), we have that
$v(gx) = v(\hat {c})$. By the finite version of property (6), we have that ![]() $v(\partial g'x') \geqslant v(g'x') \geqslant v(gx)$ for every
$v(\partial g'x') \geqslant v(g'x') \geqslant v(gx)$ for every ![]() $g'x' \in \operatorname {supp}(\hat {c})$. Since every
$g'x' \in \operatorname {supp}(\hat {c})$. Since every ![]() $g''x'' \in \operatorname {supp}(\partial \hat {c})$ is contained in
$g''x'' \in \operatorname {supp}(\partial \hat {c})$ is contained in ![]() $\operatorname {supp}(\partial g'x')$ for some
$\operatorname {supp}(\partial g'x')$ for some ![]() $g'x' \in \operatorname {supp}(\hat {c})$, we have that
$g'x' \in \operatorname {supp}(\hat {c})$, we have that ![]() $v(g''x'') \geqslant v(\partial g'x') \geqslant v(gx)$ for every
$v(g''x'') \geqslant v(\partial g'x') \geqslant v(gx)$ for every ![]() $g''x'' \in \operatorname {supp}(\partial \hat {c})$. Thus,
$g''x'' \in \operatorname {supp}(\partial \hat {c})$. Thus, ![]() $v(\partial \hat {c}) \geqslant v(\hat {c})$.
$v(\partial \hat {c}) \geqslant v(\hat {c})$.
The following lemma will be used in the proof of Theorem 5.3.
Lemma 4.2 Let ![]() $F_\bullet \rightarrow M \rightarrow 0$ (respectively,
$F_\bullet \rightarrow M \rightarrow 0$ (respectively, ![]() $F_\bullet ' \rightarrow M \rightarrow 0$) be a free resolution over
$F_\bullet ' \rightarrow M \rightarrow 0$) be a free resolution over ![]() $RG$ admissible with respect to a basis
$RG$ admissible with respect to a basis ![]() $X$ (respectively,
$X$ (respectively, ![]() $X'$), and let
$X'$), and let ![]() $v$ (respectively,
$v$ (respectively, ![]() $v'$) be the valuation extending a nontrivial character
$v'$) be the valuation extending a nontrivial character ![]() $\chi \colon G \rightarrow \mathbb {R}$. Suppose that
$\chi \colon G \rightarrow \mathbb {R}$. Suppose that ![]() $F^{(n)}$ is finitely generated, and that
$F^{(n)}$ is finitely generated, and that ![]() $\varphi \colon F \rightarrow F'$ is a homomorphism of
$\varphi \colon F \rightarrow F'$ is a homomorphism of ![]() $RG$-modules. Then:
$RG$-modules. Then:
(1)
 $\varphi$ induces a homomorphism of left
$\varphi$ induces a homomorphism of left  $RG$-modules given by
$RG$-modules given by
 \[ \widehat{\varphi} \colon \widehat{F}^{(n)} \rightarrow \widehat{F}',\quad \sum r_{g,x} gx \mapsto \sum r_{g,x} g \varphi(x); \]
\[ \widehat{\varphi} \colon \widehat{F}^{(n)} \rightarrow \widehat{F}',\quad \sum r_{g,x} gx \mapsto \sum r_{g,x} g \varphi(x); \]
(2)
 $v'(\widehat {\varphi }(\hat c)) \geqslant v(\hat {c}) + \min _{x \in X^{(n)}} \{ v'(\varphi (x)) - v(x) \}$ for every
$v'(\widehat {\varphi }(\hat c)) \geqslant v(\hat {c}) + \min _{x \in X^{(n)}} \{ v'(\varphi (x)) - v(x) \}$ for every  $\hat {c} \in F^{(n)}$.
$\hat {c} \in F^{(n)}$.
Proof. For part (1), we need to show that ![]() $\widehat {\varphi }(\hat {c})$ is a horochain for any horochain
$\widehat {\varphi }(\hat {c})$ is a horochain for any horochain ![]() $\hat {c} \in \widehat {F}^{(n)}$. To this end, let
$\hat {c} \in \widehat {F}^{(n)}$. To this end, let ![]() $\hat {c} = \sum r_{g,x} gx$, and note that there are only finitely many elements
$\hat {c} = \sum r_{g,x} gx$, and note that there are only finitely many elements ![]() $x \in X$ such that
$x \in X$ such that ![]() $gx \in \operatorname {supp}_X(\hat {c})$. If
$gx \in \operatorname {supp}_X(\hat {c})$. If ![]() $\widehat {\varphi }(\hat {c})$ is not a horochain, then the set
$\widehat {\varphi }(\hat {c})$ is not a horochain, then the set ![]() $\{ gx \in \operatorname {supp}_X(\hat {c}) : v'(g\varphi (x)) \leqslant t \}$ is infinite for some
$\{ gx \in \operatorname {supp}_X(\hat {c}) : v'(g\varphi (x)) \leqslant t \}$ is infinite for some ![]() $t \in \mathbb {R}$. Since
$t \in \mathbb {R}$. Since ![]() $F^{(n)}$ is finitely generated, there is some fixed
$F^{(n)}$ is finitely generated, there is some fixed ![]() $y \in X$ such that
$y \in X$ such that ![]() $v'(g\varphi (y)) \leqslant t$ and
$v'(g\varphi (y)) \leqslant t$ and ![]() $gy \in \operatorname {supp}_X(\hat {c})$ for infinitely many values of
$gy \in \operatorname {supp}_X(\hat {c})$ for infinitely many values of ![]() $g \in G$. But then
$g \in G$. But then
 \begin{align*} v(gy) &= \chi(g) + v(y) \\ &= \chi(g) + v'(\varphi(y)) + v(y) - v'(\varphi(y))\\ &= v'(g\varphi(y)) + v(y) - v'(\varphi(y)) \\ &\leqslant t + v(y) - v'(\varphi(y)) \end{align*}
\begin{align*} v(gy) &= \chi(g) + v(y) \\ &= \chi(g) + v'(\varphi(y)) + v(y) - v'(\varphi(y))\\ &= v'(g\varphi(y)) + v(y) - v'(\varphi(y)) \\ &\leqslant t + v(y) - v'(\varphi(y)) \end{align*}
for infinitely many ![]() $gy \in \operatorname {supp}_X(\hat {c})$, but
$gy \in \operatorname {supp}_X(\hat {c})$, but ![]() $\hat {c}$ is a horochain.
$\hat {c}$ is a horochain.
For part (2), write ![]() $\hat {c} = \sum _{x\in X^{(n)}} \hat {c}_x$, where
$\hat {c} = \sum _{x\in X^{(n)}} \hat {c}_x$, where ![]() $\hat {c}_x = \sum _{g \in G} r_{g,x} g x$. Then
$\hat {c}_x = \sum _{g \in G} r_{g,x} g x$. Then
 \begin{align*} v'(\widehat{\varphi}(\hat{c})) &\geqslant \min_{x \in X^{(n)}}\{ v'(\widehat{\varphi}(\hat{c}_x))\} \\ &\geqslant \min_{x \in X^{(n)}} \{ \inf\{ v'(g\varphi(x)) : gx \in \operatorname{supp} \hat{c}_x \} \} \\ &= \min_{x \in X^{(n)}}\{ \inf\{ v(gx) : gx \in \operatorname{supp} \hat{c}_x \} + v'(\varphi(x)) - v(x) \} \\ &= \min_{x \in X^{(n)}} \{ v(\hat{c}_x) + v'(\varphi(x)) - v(x) \} \\ &\geqslant \min_{x \in X^{(n)}} \{ v(\hat{c}_x) \} + \min_{x \in X^{(n)}}\{ v'(\varphi(x)) - v(x) \} \\ &= v(\hat{c}) + \min_{x \in X^{(n)}} \{ v'(\varphi(x)) - v(x) \}.\end{align*}
\begin{align*} v'(\widehat{\varphi}(\hat{c})) &\geqslant \min_{x \in X^{(n)}}\{ v'(\widehat{\varphi}(\hat{c}_x))\} \\ &\geqslant \min_{x \in X^{(n)}} \{ \inf\{ v'(g\varphi(x)) : gx \in \operatorname{supp} \hat{c}_x \} \} \\ &= \min_{x \in X^{(n)}}\{ \inf\{ v(gx) : gx \in \operatorname{supp} \hat{c}_x \} + v'(\varphi(x)) - v(x) \} \\ &= \min_{x \in X^{(n)}} \{ v(\hat{c}_x) + v'(\varphi(x)) - v(x) \} \\ &\geqslant \min_{x \in X^{(n)}} \{ v(\hat{c}_x) \} + \min_{x \in X^{(n)}}\{ v'(\varphi(x)) - v(x) \} \\ &= v(\hat{c}) + \min_{x \in X^{(n)}} \{ v'(\varphi(x)) - v(x) \}.\end{align*}
Note that Lemma 4.2(2) applies to chains in ![]() $F$ since these are just finite horo-chains. We will use this in the proof Theorem 5.3.
$F$ since these are just finite horo-chains. We will use this in the proof Theorem 5.3.
5. Characterisations of the  $\Sigma$-invariant
$\Sigma$-invariant
We introduce the invariants ![]() $\Sigma ^n_R(G;M)$, which are generalisations of the classical BNS invariant [Reference Bieri, Neumann and StrebelBNS87] and its higher-dimensional analogues [Reference Bieri and RenzBR88]. The only difference is that we work over a general ring
$\Sigma ^n_R(G;M)$, which are generalisations of the classical BNS invariant [Reference Bieri, Neumann and StrebelBNS87] and its higher-dimensional analogues [Reference Bieri and RenzBR88]. The only difference is that we work over a general ring ![]() $R$, whereas the higher BNS invariants are defined over
$R$, whereas the higher BNS invariants are defined over ![]() $\mathbb {Z}$.
$\mathbb {Z}$.
Let ![]() $G$ be a group. We declare two characters
$G$ be a group. We declare two characters ![]() $\chi,\chi ' \colon G \rightarrow \mathbb {R}$ to be equivalent if
$\chi,\chi ' \colon G \rightarrow \mathbb {R}$ to be equivalent if ![]() $\chi = \alpha \cdot \chi '$ for some
$\chi = \alpha \cdot \chi '$ for some ![]() $\alpha > 0$ and let
$\alpha > 0$ and let ![]() $S(G)$ denote the set of equivalence classes of nonzero characters. We call
$S(G)$ denote the set of equivalence classes of nonzero characters. We call ![]() $S(G)$ the character sphere of
$S(G)$ the character sphere of ![]() $G$, because it can be given the topology of a sphere when
$G$, because it can be given the topology of a sphere when ![]() $G$ is finitely generated.
$G$ is finitely generated.
Definition 5.1 ( $\Sigma$-invariants)
$\Sigma$-invariants)
Let ![]() $M$ be an
$M$ be an ![]() $RG$-module. Then define
$RG$-module. Then define
where ![]() $G_\chi = \{ g \in G : \chi (g) \geqslant 0 \}$. Note that
$G_\chi = \{ g \in G : \chi (g) \geqslant 0 \}$. Note that ![]() $G_\chi = G_{\chi '}$ if
$G_\chi = G_{\chi '}$ if ![]() $[\chi ] = [\chi ']$, so
$[\chi ] = [\chi ']$, so ![]() $\Sigma ^n_R(G;M)$ is well-defined.
$\Sigma ^n_R(G;M)$ is well-defined.
Definition 5.2 (Novikov ring)
Let ![]() $G$ be a group, let
$G$ be a group, let ![]() $R$ be a ring and let
$R$ be a ring and let ![]() $\chi \colon G \rightarrow \mathbb {R}$ be a character. Then the Novikov ring
$\chi \colon G \rightarrow \mathbb {R}$ be a character. Then the Novikov ring ![]() $\widehat {RG}^\chi$ is the set of formal sums
$\widehat {RG}^\chi$ is the set of formal sums
such that ![]() $\{ g \in G : r_g \neq 0 \ \text {and} \ \varphi (g) \leqslant t \}$ is finite for every
$\{ g \in G : r_g \neq 0 \ \text {and} \ \varphi (g) \leqslant t \}$ is finite for every ![]() $t \in \mathbb {R}$. We give
$t \in \mathbb {R}$. We give ![]() $\widehat {RG}^\chi$ a ring structure by defining
$\widehat {RG}^\chi$ a ring structure by defining ![]() $rg + r'g := (r + r')g$ and
$rg + r'g := (r + r')g$ and ![]() $rg \cdot r'g' := rr' gg'$ for
$rg \cdot r'g' := rr' gg'$ for ![]() $r,r' \in R$,
$r,r' \in R$, ![]() $g,g' \in G$, and extending multiplication to all of
$g,g' \in G$, and extending multiplication to all of ![]() $\widehat {RG}^\chi$ in the obvious way.
$\widehat {RG}^\chi$ in the obvious way.
Theorem 5.3 gives several characterisations of the ![]() $\Sigma$-invariants and is the main technical tool we will need to prove Theorem 6.7. More specifically, we will need the characterisation of
$\Sigma$-invariants and is the main technical tool we will need to prove Theorem 6.7. More specifically, we will need the characterisation of ![]() $\Sigma _R^n(G;M)$ in terms of the vanishing of Novikov homology; this is the equivalence of parts (1) and (5) in the following theorem, which should be thought of as a higher-dimensional version of Sikorav's theorem [Reference SikoravSik87].
$\Sigma _R^n(G;M)$ in terms of the vanishing of Novikov homology; this is the equivalence of parts (1) and (5) in the following theorem, which should be thought of as a higher-dimensional version of Sikorav's theorem [Reference SikoravSik87].
Theorem 5.3 Let ![]() $R$ be a ring, let
$R$ be a ring, let ![]() $M$ be a left
$M$ be a left ![]() $RG$-module of type
$RG$-module of type ![]() $\mathtt {FP}_n$ and let
$\mathtt {FP}_n$ and let ![]() $\chi \colon G \rightarrow \mathbb {R}$ be a nontrivial character. Let
$\chi \colon G \rightarrow \mathbb {R}$ be a nontrivial character. Let ![]() $F_\bullet \rightarrow M \rightarrow 0$ be a free resolution admissible with respect to a basis
$F_\bullet \rightarrow M \rightarrow 0$ be a free resolution admissible with respect to a basis ![]() $X = \bigcup _{i = 0}^\infty X_i$ and with finitely generated
$X = \bigcup _{i = 0}^\infty X_i$ and with finitely generated ![]() $n$-skeleton
$n$-skeleton ![]() $F^{(n)}$. Let
$F^{(n)}$. Let ![]() $v \colon F \rightarrow \mathbb {R}_\infty$ be the valuation extending
$v \colon F \rightarrow \mathbb {R}_\infty$ be the valuation extending ![]() $\chi$ with respect to
$\chi$ with respect to ![]() $X$. The following are equivalent:
$X$. The following are equivalent:
(1)
 $[\chi ] \in \Sigma _R^n(G;M)$;
$[\chi ] \in \Sigma _R^n(G;M)$;(2)
 $F_\bullet ^v \rightarrow M \rightarrow 0$ is essentially acyclic in dimensions
$F_\bullet ^v \rightarrow M \rightarrow 0$ is essentially acyclic in dimensions  $-1, \ldots, n-1$;
$-1, \ldots, n-1$;(3) there is a chain map
 $\varphi \colon F \rightarrow F$ lifting the identity
$\varphi \colon F \rightarrow F$ lifting the identity  $\operatorname {id}_M$ such that
$\operatorname {id}_M$ such that  $v(\varphi (c)) > v(c)$ for every
$v(\varphi (c)) > v(c)$ for every  $c \in F^{(n)}$;
$c \in F^{(n)}$;(4)
 $F_\bullet \rightarrow M \rightarrow 0$ is horo-acyclic in dimensions
$F_\bullet \rightarrow M \rightarrow 0$ is horo-acyclic in dimensions  $0, \ldots, n$ with respect to
$0, \ldots, n$ with respect to  $v$;
$v$;(5)
 $\operatorname {Tor}_i^{RG}(\widehat {RG}^\chi,M) = 0$ for all
$\operatorname {Tor}_i^{RG}(\widehat {RG}^\chi,M) = 0$ for all  $0 \leqslant i \leqslant n$.
$0 \leqslant i \leqslant n$.
The strategy of the proof will be as follows: we begin by proving (2) ![]() $\Rightarrow$ (3)
$\Rightarrow$ (3) ![]() $\Rightarrow$ (4)
$\Rightarrow$ (4) ![]() $\Rightarrow$ (2). This is done by Schweitzer in the appendix of [Reference BieriBie07] in the case
$\Rightarrow$ (2). This is done by Schweitzer in the appendix of [Reference BieriBie07] in the case ![]() $R = \mathbb {Z}$. Once this is done, we prove the equivalence of parts (4) and (5), again following Schweitzer. Finally, we prove the equivalence of parts (1) and (2) following the appendix to Theorem 3.2 in [Reference Bieri and RenzBR88], where again this is done in the case
$R = \mathbb {Z}$. Once this is done, we prove the equivalence of parts (4) and (5), again following Schweitzer. Finally, we prove the equivalence of parts (1) and (2) following the appendix to Theorem 3.2 in [Reference Bieri and RenzBR88], where again this is done in the case ![]() $R = \mathbb {Z}$. The proofs below are essentially the same as those given in the references just cited; there is no crucial dependence on the coefficient ring
$R = \mathbb {Z}$. The proofs below are essentially the same as those given in the references just cited; there is no crucial dependence on the coefficient ring ![]() $R$.
$R$.
Proof Proof of (2)  $\Rightarrow$ (3)
$\Rightarrow$ (3)
Assume that ![]() $F_\bullet ^v \rightarrow M \rightarrow 0$ is essentially acyclic in dimensions
$F_\bullet ^v \rightarrow M \rightarrow 0$ is essentially acyclic in dimensions ![]() $\leqslant n-1$ and let
$\leqslant n-1$ and let ![]() $D > 0$ be a constant such that for each
$D > 0$ be a constant such that for each ![]() $k < n$ and every cycle
$k < n$ and every cycle ![]() $z \in F_k$, there is a chain
$z \in F_k$, there is a chain ![]() $c \in F_{k+1}$ with
$c \in F_{k+1}$ with ![]() $\partial c = z$ and
$\partial c = z$ and ![]() $D \geqslant v(z) - v(c)$. We will construct a chain map
$D \geqslant v(z) - v(c)$. We will construct a chain map ![]() $\varphi \colon F \rightarrow F$ lifting
$\varphi \colon F \rightarrow F$ lifting ![]() $\operatorname {id}_M$ such that
$\operatorname {id}_M$ such that ![]() $v(\varphi (c)) > v(c) + (n - k)D$ for every
$v(\varphi (c)) > v(c) + (n - k)D$ for every ![]() $c \in F^{(k)}$, which implies part (3).
$c \in F^{(k)}$, which implies part (3).
We define ![]() $\varphi$ on
$\varphi$ on ![]() $F^{(k)}$ by induction on
$F^{(k)}$ by induction on ![]() $k$. For the base case, let
$k$. For the base case, let ![]() $x \in X_0$ be arbitrary and fix some
$x \in X_0$ be arbitrary and fix some ![]() $g \in G$ such that
$g \in G$ such that ![]() $\chi (g) > (n+1)D$. The element
$\chi (g) > (n+1)D$. The element ![]() $g^{-1}\partial x \in M$ is a cycle, so there is some
$g^{-1}\partial x \in M$ is a cycle, so there is some ![]() $c_x \in F_0$ such that
$c_x \in F_0$ such that ![]() $\partial c_x = g^{-1} \partial x$ and
$\partial c_x = g^{-1} \partial x$ and ![]() $D \geqslant v(g^{-1} \partial x) - v(c_x) = -v(c_x)$, since
$D \geqslant v(g^{-1} \partial x) - v(c_x) = -v(c_x)$, since ![]() $v|_{M \setminus \{0\}} = 0$. Define
$v|_{M \setminus \{0\}} = 0$. Define ![]() $\varphi$ on
$\varphi$ on ![]() $F^{(0)}$ by setting
$F^{(0)}$ by setting ![]() $\varphi (x) = gc_x$ for each
$\varphi (x) = gc_x$ for each ![]() $x \in X_0$. It is clear that
$x \in X_0$. It is clear that ![]() $\mathrm {id}_M \partial = \partial \varphi$ on
$\mathrm {id}_M \partial = \partial \varphi$ on ![]() $F^{(0)}$. By Lemma 4.2(2),
$F^{(0)}$. By Lemma 4.2(2),
for every ![]() $c \in F^{(0)}$.
$c \in F^{(0)}$.
Let ![]() $k > 0$ and suppose
$k > 0$ and suppose ![]() $\varphi$ is defined on
$\varphi$ is defined on ![]() $F^{(k-1)}$ such that it lifts
$F^{(k-1)}$ such that it lifts ![]() $\operatorname {id}_M$ and
$\operatorname {id}_M$ and ![]() $v(\varphi (c)) > v(c) + (n - k + 1)D$ for all
$v(\varphi (c)) > v(c) + (n - k + 1)D$ for all ![]() $c \in F^{(k-1)}$. Let
$c \in F^{(k-1)}$. Let ![]() $x \in X_k$ and note that
$x \in X_k$ and note that ![]() $\varphi (\partial x)$ is a cycle. By essential acyclicity, there is a chain
$\varphi (\partial x)$ is a cycle. By essential acyclicity, there is a chain ![]() $d_x \in F_k$ such that
$d_x \in F_k$ such that ![]() $\partial d_x = \varphi (\partial x)$ and
$\partial d_x = \varphi (\partial x)$ and ![]() $D \geqslant v(\varphi (\partial x)) - v(d_x)$. Define
$D \geqslant v(\varphi (\partial x)) - v(d_x)$. Define ![]() $\varphi$ on
$\varphi$ on ![]() $F^{(k)}$ by setting
$F^{(k)}$ by setting ![]() $\varphi (x) = d_x$. Then
$\varphi (x) = d_x$. Then ![]() $\varphi \partial = \partial \varphi$ by construction, and for every
$\varphi \partial = \partial \varphi$ by construction, and for every ![]() $x \in X_k$ we have
$x \in X_k$ we have
 \begin{align*} v(\varphi(x)) - v(x) &= v(d_x) - v(x) \\ &\geqslant v(\varphi(\partial x)) - v(x) - D \\ &= v(\varphi(\partial x)) - v(\partial x) - D \\ &> (n-k)D \end{align*}
\begin{align*} v(\varphi(x)) - v(x) &= v(d_x) - v(x) \\ &\geqslant v(\varphi(\partial x)) - v(x) - D \\ &= v(\varphi(\partial x)) - v(\partial x) - D \\ &> (n-k)D \end{align*}
by induction. By Lemma 4.2(2), we have
We pause here to prove a lemma that will immediately imply (3) ![]() $\Rightarrow$ (4) and will be useful in the proofs of (4)
$\Rightarrow$ (4) and will be useful in the proofs of (4) ![]() $\Rightarrow$ (2) and (4)
$\Rightarrow$ (2) and (4) ![]() $\Rightarrow$ (5). We recall that the maps
$\Rightarrow$ (5). We recall that the maps ![]() $\widehat {H}$ and
$\widehat {H}$ and ![]() $\widehat {\varphi }$ that appear in the statement of the lemma below are defined in Lemma 4.2.
$\widehat {\varphi }$ that appear in the statement of the lemma below are defined in Lemma 4.2.
Lemma 5.4 With the assumptions of Theorem 5.3, let ![]() $\varphi \colon F \rightarrow F$ be a chain map lifting
$\varphi \colon F \rightarrow F$ be a chain map lifting ![]() $\operatorname {id}_M$ such that
$\operatorname {id}_M$ such that ![]() $v(\varphi (c)) > v(c)$ for all
$v(\varphi (c)) > v(c)$ for all ![]() $c \in F^{(n)}$ and let
$c \in F^{(n)}$ and let ![]() $H \colon F \rightarrow F$ be a chain homotopy such that
$H \colon F \rightarrow F$ be a chain homotopy such that ![]() $\partial H + H \partial = \operatorname {id}_{F} - \varphi$. Let
$\partial H + H \partial = \operatorname {id}_{F} - \varphi$. Let ![]() $\hat {z} \in \widehat {F}^{(n)}$ be a horocycle and define
$\hat {z} \in \widehat {F}^{(n)}$ be a horocycle and define ![]() $\hat {c}_{\hat {z}} := \sum _{i = 0}^\infty \widehat {H} \widehat {\varphi }^i(\hat {z})$. Then
$\hat {c}_{\hat {z}} := \sum _{i = 0}^\infty \widehat {H} \widehat {\varphi }^i(\hat {z})$. Then ![]() $\hat {c}_{\hat {z}}$ is a horochain and
$\hat {c}_{\hat {z}}$ is a horochain and ![]() $\partial \hat {c}_{\hat {z}} = \hat {z}$.
$\partial \hat {c}_{\hat {z}} = \hat {z}$.
Proof. By Lemma 4.2(2) there are constants ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ such that
$\beta$ such that
for every horochain ![]() $\hat {c} \in \widehat {F}^{(n)}$. Moreover,
$\hat {c} \in \widehat {F}^{(n)}$. Moreover, ![]() $\alpha > 0$ since
$\alpha > 0$ since ![]() $v(\varphi (f)) > v(f)$ for every
$v(\varphi (f)) > v(f)$ for every ![]() $f \in F^{(n)}$. To see that
$f \in F^{(n)}$. To see that ![]() $\hat {c}$ is a horochain, by induction we have
$\hat {c}$ is a horochain, by induction we have ![]() $v(\widehat {H}\widehat {\varphi }^i(\hat {z})) \geqslant v(\hat {z}) + i\alpha + \beta$, so for all
$v(\widehat {H}\widehat {\varphi }^i(\hat {z})) \geqslant v(\hat {z}) + i\alpha + \beta$, so for all ![]() $t \in \mathbb {R}$ there are only finitely many integers
$t \in \mathbb {R}$ there are only finitely many integers ![]() $i \geqslant 0$ such that
$i \geqslant 0$ such that ![]() $v(\widehat {H} \widehat {\varphi }^i(\hat {z})) \leqslant t$. Since
$v(\widehat {H} \widehat {\varphi }^i(\hat {z})) \leqslant t$. Since ![]() $\operatorname {supp}(\hat {c}_{\hat {z}}) \subseteq \bigcup _{i=0}^\infty \operatorname {supp}(\widehat {H}\widehat {\varphi }^i(\hat {z}))$ and each
$\operatorname {supp}(\hat {c}_{\hat {z}}) \subseteq \bigcup _{i=0}^\infty \operatorname {supp}(\widehat {H}\widehat {\varphi }^i(\hat {z}))$ and each ![]() $\widehat {H} \widehat {\varphi }^i(\hat {z})$ is a horochain, it follows that there are only finitely many
$\widehat {H} \widehat {\varphi }^i(\hat {z})$ is a horochain, it follows that there are only finitely many ![]() $gx \in \operatorname {supp} \hat {c}$ such that
$gx \in \operatorname {supp} \hat {c}$ such that ![]() $v(gx) \leqslant t$, so
$v(gx) \leqslant t$, so ![]() $\hat {c}$ is a horochain.
$\hat {c}$ is a horochain.
Finally, we have
 \[ \partial\hat{c} = \sum_{i=0}^\infty \partial \widehat{H} \widehat{\varphi}^i(\hat{z}) = \sum_{i=0}^\infty (\operatorname{id}_{\widehat{F}^{(n)}} - \widehat{\varphi} - \widehat{H}\partial) \widehat{\varphi}^i(\hat{z}) = \sum_{i=0}^\infty (\widehat{\varphi}^i - \widehat{\varphi}^{i+1})(\hat{z}) = \hat{z}.\]
\[ \partial\hat{c} = \sum_{i=0}^\infty \partial \widehat{H} \widehat{\varphi}^i(\hat{z}) = \sum_{i=0}^\infty (\operatorname{id}_{\widehat{F}^{(n)}} - \widehat{\varphi} - \widehat{H}\partial) \widehat{\varphi}^i(\hat{z}) = \sum_{i=0}^\infty (\widehat{\varphi}^i - \widehat{\varphi}^{i+1})(\hat{z}) = \hat{z}.\]
Proof Proof of (3)  $\Rightarrow$ (4)
$\Rightarrow$ (4)
By [Reference BrownBro94, Lemma I.7.4], there is a chain homotopy ![]() $H \colon F \rightarrow F$ such that
$H \colon F \rightarrow F$ such that ![]() $\partial H + H \partial = \operatorname {id}_F - \varphi$. If
$\partial H + H \partial = \operatorname {id}_F - \varphi$. If ![]() $\hat {z} \in \widehat {F}^{(n)}$ is a horocycle, then
$\hat {z} \in \widehat {F}^{(n)}$ is a horocycle, then ![]() $\partial \hat {c}_{\hat {z}} = \hat z$ by Lemma 5.4.
$\partial \hat {c}_{\hat {z}} = \hat z$ by Lemma 5.4.
Proof Proof of (4)  $\Rightarrow$ (2)
$\Rightarrow$ (2)
We will prove that ![]() $F_\bullet ^v \rightarrow M \rightarrow 0$ is essentially acyclic in dimension
$F_\bullet ^v \rightarrow M \rightarrow 0$ is essentially acyclic in dimension ![]() $k$ for all
$k$ for all ![]() $k < n$ by induction on
$k < n$ by induction on ![]() $k$. For the base case, we show that
$k$. For the base case, we show that ![]() $F_\bullet ^v \rightarrow M \rightarrow 0$ is exact at
$F_\bullet ^v \rightarrow M \rightarrow 0$ is exact at ![]() $M$, which implies essential acyclicity in dimension
$M$, which implies essential acyclicity in dimension ![]() $-1$. Let
$-1$. Let ![]() $m \in M$. By exactness of
$m \in M$. By exactness of ![]() $F_\bullet \rightarrow M \rightarrow 0$, there is a chain
$F_\bullet \rightarrow M \rightarrow 0$, there is a chain ![]() $c \in F_0$ such that
$c \in F_0$ such that ![]() $\partial c = m$. By horo-acyclicity in dimension
$\partial c = m$. By horo-acyclicity in dimension ![]() $0$, there is some horochain
$0$, there is some horochain ![]() $\hat {c} \in \widehat {F}_1$ such that
$\hat {c} \in \widehat {F}_1$ such that ![]() $\partial \hat {c} = c$. There are
$\partial \hat {c} = c$. There are ![]() $c_{-} \in F_1$ and
$c_{-} \in F_1$ and ![]() $\hat {c}_+ \in \widehat {F}_1$ such that
$\hat {c}_+ \in \widehat {F}_1$ such that ![]() $\hat {c} = c_{-} + \hat {c}_+$, where
$\hat {c} = c_{-} + \hat {c}_+$, where ![]() $v(c_{-}) < 0$ and
$v(c_{-}) < 0$ and ![]() $v(\hat {c}_+) \geqslant 0$. Then
$v(\hat {c}_+) \geqslant 0$. Then ![]() $\partial (c - \partial c_-) = m$ and
$\partial (c - \partial c_-) = m$ and
This shows that ![]() $c - \partial c_0 \in F_0^v$, which proves that
$c - \partial c_0 \in F_0^v$, which proves that ![]() $F_\bullet ^v \rightarrow M \rightarrow 0$ is exact at
$F_\bullet ^v \rightarrow M \rightarrow 0$ is exact at ![]() $M$.
$M$.
Let ![]() $k > -1$ and suppose that
$k > -1$ and suppose that ![]() $F_\bullet ^v \rightarrow M \rightarrow 0$ is essentially acyclic in dimensions
$F_\bullet ^v \rightarrow M \rightarrow 0$ is essentially acyclic in dimensions ![]() $< k$. By (2)
$< k$. By (2) ![]() $\Rightarrow$ (3) applied at
$\Rightarrow$ (3) applied at ![]() $k-1$, there is a chain map
$k-1$, there is a chain map ![]() $\varphi \colon F \rightarrow F$ lifting
$\varphi \colon F \rightarrow F$ lifting ![]() $\operatorname {id}_M$ such that
$\operatorname {id}_M$ such that ![]() $v(\varphi (c)) > v(c)$ for all
$v(\varphi (c)) > v(c)$ for all ![]() $c \in F^{(k)}$. Since
$c \in F^{(k)}$. Since ![]() $\operatorname {id}_F$ and
$\operatorname {id}_F$ and ![]() $\varphi$ both lift
$\varphi$ both lift ![]() $\operatorname {id}_M$ and
$\operatorname {id}_M$ and ![]() $F_\bullet \rightarrow M \rightarrow 0$ is acyclic, there is a chain homotopy
$F_\bullet \rightarrow M \rightarrow 0$ is acyclic, there is a chain homotopy ![]() $H \colon F \rightarrow F$ such that
$H \colon F \rightarrow F$ such that ![]() $\partial H + H \partial = \operatorname {id}_{F} - \varphi$ (see [Reference BrownBro94, Lemma I.7.4]). As in the proof of Lemma 5.4, there are constants
$\partial H + H \partial = \operatorname {id}_{F} - \varphi$ (see [Reference BrownBro94, Lemma I.7.4]). As in the proof of Lemma 5.4, there are constants ![]() $\alpha > 0$ and
$\alpha > 0$ and ![]() $\beta < 0$ such that
$\beta < 0$ such that
for every ![]() $c \in F^{(k)}$.
$c \in F^{(k)}$.
Let ![]() $z \in F^v_{k}$ be a cycle. Since
$z \in F^v_{k}$ be a cycle. Since ![]() $F_\bullet \rightarrow M \rightarrow 0$ is acyclic, there is some
$F_\bullet \rightarrow M \rightarrow 0$ is acyclic, there is some ![]() $d \in F_{k+1}$ such that
$d \in F_{k+1}$ such that ![]() $\partial d = z$. Consider the horocycle
$\partial d = z$. Consider the horocycle ![]() $\hat {z} := d - \hat {d}_z$, where
$\hat {z} := d - \hat {d}_z$, where ![]() $\hat {d}_z = \sum _{i = 0}^\infty H\varphi ^i(z)$ is defined as in Lemma 5.4. Note that
$\hat {d}_z = \sum _{i = 0}^\infty H\varphi ^i(z)$ is defined as in Lemma 5.4. Note that
for every ![]() $i \geqslant 0$, and therefore that
$i \geqslant 0$, and therefore that ![]() $v(\hat {d}_z) \geqslant \beta$. By horo-acyclicity in dimension
$v(\hat {d}_z) \geqslant \beta$. By horo-acyclicity in dimension ![]() $k+1$, there is a
$k+1$, there is a ![]() $(k+2)$-horochain
$(k+2)$-horochain ![]() $\hat {d}$ such that
$\hat {d}$ such that ![]() $\partial \hat {d} = \hat {z}$. As in the base case, there are
$\partial \hat {d} = \hat {z}$. As in the base case, there are ![]() $d_- \in F_{k+2}$ and
$d_- \in F_{k+2}$ and ![]() $\hat {d}_+ \in \widehat {F}_{k+2}$ such that
$\hat {d}_+ \in \widehat {F}_{k+2}$ such that ![]() $\hat {d} = d_- + \hat {d}_+$, where
$\hat {d} = d_- + \hat {d}_+$, where ![]() $v(d_-) < 0$ and
$v(d_-) < 0$ and ![]() $v(\hat {d}_+) \geqslant 0$. Then
$v(\hat {d}_+) \geqslant 0$. Then ![]() $\partial (d - \partial d_-) = \partial d = z$, and
$\partial (d - \partial d_-) = \partial d = z$, and
 \begin{align*} v(d - \partial d_-) &= v(\hat{d}_z + \hat{z} - \partial(\hat{d} - \hat{d}_+)) \\ &= v(\hat{d}_z + \partial \hat{d}_+) \\ &\geqslant \min\{ v(\hat{d}_z), v(\partial \hat{d}_+) \} \\ &\geqslant \beta \end{align*}
\begin{align*} v(d - \partial d_-) &= v(\hat{d}_z + \hat{z} - \partial(\hat{d} - \hat{d}_+)) \\ &= v(\hat{d}_z + \partial \hat{d}_+) \\ &\geqslant \min\{ v(\hat{d}_z), v(\partial \hat{d}_+) \} \\ &\geqslant \beta \end{align*}
since ![]() $v(\hat {d}_z) \geqslant \beta$ and
$v(\hat {d}_z) \geqslant \beta$ and ![]() $v(\partial d_\infty ) \geqslant v(d_\infty ) \geqslant 0 > \beta$. Letting
$v(\partial d_\infty ) \geqslant v(d_\infty ) \geqslant 0 > \beta$. Letting ![]() $D = -\beta$ in the definition of essential acyclicity, we see that
$D = -\beta$ in the definition of essential acyclicity, we see that ![]() $F_\bullet ^v \rightarrow M \rightarrow 0$ is essentially acyclic in dimension
$F_\bullet ^v \rightarrow M \rightarrow 0$ is essentially acyclic in dimension ![]() $k$.
$k$.
Proof Proof of (5)  $\Rightarrow$ (4)
$\Rightarrow$ (4)
Suppose that ![]() $\operatorname {Tor}_i^{RG}(\widehat {RG}^\chi,M) = 0$ for
$\operatorname {Tor}_i^{RG}(\widehat {RG}^\chi,M) = 0$ for ![]() $0 \leqslant i \leqslant n$. Consider the chain map
$0 \leqslant i \leqslant n$. Consider the chain map
of left ![]() $RG$-modules. It is clear that
$RG$-modules. It is clear that ![]() $\psi$ is injective. We claim that
$\psi$ is injective. We claim that ![]() $\psi$ induces an isomorphism
$\psi$ induces an isomorphism ![]() $\widehat {RG}^\chi \otimes _{RG} F^{(n)} \rightarrow \widehat {F}^{(n)}$. To see this, simply note that for an arbitrary horochain
$\widehat {RG}^\chi \otimes _{RG} F^{(n)} \rightarrow \widehat {F}^{(n)}$. To see this, simply note that for an arbitrary horochain
in ![]() $\widehat {F}^{(n)}$, we have
$\widehat {F}^{(n)}$, we have
 \[ \sum_{x \in X^{(n)}} \bigg(\sum_{g\in G} r_{g,x} g \bigg) \otimes x \overset{\varphi}{\mapsto} \hat{c}. \]
\[ \sum_{x \in X^{(n)}} \bigg(\sum_{g\in G} r_{g,x} g \bigg) \otimes x \overset{\varphi}{\mapsto} \hat{c}. \]
The horochain condition implies that the sums ![]() $\sum _{g\in G} r_{g,x} g$ are elements of
$\sum _{g\in G} r_{g,x} g$ are elements of ![]() $\widehat {RG}^\chi$. Thus,
$\widehat {RG}^\chi$. Thus, ![]() $\psi$ is surjective on the
$\psi$ is surjective on the ![]() $n$-skeleta and is therefore an isomorphism. Note that this only works because
$n$-skeleta and is therefore an isomorphism. Note that this only works because ![]() $X^{(n)}$ is finite; in general, we cannot expect
$X^{(n)}$ is finite; in general, we cannot expect ![]() $\psi$ to be surjective since the support of a horochain might intersect infinitely many of the modules
$\psi$ to be surjective since the support of a horochain might intersect infinitely many of the modules ![]() $F_n$. Since
$F_n$. Since ![]() $\operatorname {Tor}_i^{RG}(\widehat {RG}^\chi \otimes _{RG} F, M) = 0$ for all
$\operatorname {Tor}_i^{RG}(\widehat {RG}^\chi \otimes _{RG} F, M) = 0$ for all ![]() $0 \leqslant i \leqslant n$, we conclude that
$0 \leqslant i \leqslant n$, we conclude that ![]() $\operatorname {Tor}_i(\widehat {F}, M) = 0$ for
$\operatorname {Tor}_i(\widehat {F}, M) = 0$ for ![]() $0 \leqslant i \leqslant n$ as well.
$0 \leqslant i \leqslant n$ as well.
Proof Proof of (4)  $\Rightarrow$ (5)
$\Rightarrow$ (5)
The map ![]() $\psi$ defined above is an isomorphism of the
$\psi$ defined above is an isomorphism of the ![]() $n$-skeleta, so we immediately have that
$n$-skeleta, so we immediately have that ![]() $\operatorname {Tor}_i^{RG}(\widehat {RG}^\chi,M) = 0$ for
$\operatorname {Tor}_i^{RG}(\widehat {RG}^\chi,M) = 0$ for ![]() $0 \leqslant i \leqslant n-1$. Since
$0 \leqslant i \leqslant n-1$. Since ![]() $\psi$ is not necessarily surjective as a map of the
$\psi$ is not necessarily surjective as a map of the ![]() $(n+1)$-skeleta, we must work harder to show that
$(n+1)$-skeleta, we must work harder to show that ![]() $\operatorname {Tor}_n^{RG}(\widehat {RG}^\chi,M) = 0$. Let
$\operatorname {Tor}_n^{RG}(\widehat {RG}^\chi,M) = 0$. Let ![]() $z \in \widehat {RG}^\chi \otimes _{RG} F_n$ be an
$z \in \widehat {RG}^\chi \otimes _{RG} F_n$ be an ![]() $n$-cycle, and let
$n$-cycle, and let ![]() $\hat {z} = \psi (z)$. Since we are assuming that part (4) holds, we may also assume that part (3) holds and use the horochain
$\hat {z} = \psi (z)$. Since we are assuming that part (4) holds, we may also assume that part (3) holds and use the horochain ![]() $\hat {c}_{\hat {z}}$ from Lemma 5.4. Since
$\hat {c}_{\hat {z}}$ from Lemma 5.4. Since ![]() $\hat {c}_{\hat {z}} \in \widehat {H}(\widehat {F}_n)$, we have that
$\hat {c}_{\hat {z}} \in \widehat {H}(\widehat {F}_n)$, we have that ![]() $\hat {c}_{\hat {z}}$ is in the
$\hat {c}_{\hat {z}}$ is in the ![]() $\widehat {RG}^\chi$-submodule of
$\widehat {RG}^\chi$-submodule of ![]() $\widehat {F}_{n+1}$ generated by
$\widehat {F}_{n+1}$ generated by ![]() $\widehat {H}(X_n)$ and, thus,
$\widehat {H}(X_n)$ and, thus, ![]() $\hat {c}_{\hat {z}} \in \operatorname {im} \psi$ since this is a finite set. Let
$\hat {c}_{\hat {z}} \in \operatorname {im} \psi$ since this is a finite set. Let ![]() $c \in \widehat {RG}^\chi \otimes _{RG} F_{n+1}$ such that
$c \in \widehat {RG}^\chi \otimes _{RG} F_{n+1}$ such that ![]() $\psi (c) = \hat {c}_{\hat {z}}$. Then
$\psi (c) = \hat {c}_{\hat {z}}$. Then ![]() $\psi \partial (c) = \partial \psi (c) = \partial \hat {c}_{\hat {z}} = \hat {z}$. However,
$\psi \partial (c) = \partial \psi (c) = \partial \hat {c}_{\hat {z}} = \hat {z}$. However, ![]() $\psi$ is injective, so
$\psi$ is injective, so ![]() $\partial c = z$, proving that
$\partial c = z$, proving that ![]() $\operatorname {Tor}_n^{RG}(\widehat {RG}^\chi,M) = 0$.
$\operatorname {Tor}_n^{RG}(\widehat {RG}^\chi,M) = 0$.
We pause again before proving the equivalence of parts (1) and (2) to prove another lemma.
Lemma 5.5 Free ![]() $RG$-modules are flat over
$RG$-modules are flat over ![]() $RG_\chi$.
$RG_\chi$.
Proof. It suffices to prove that ![]() $RG$ is flat as an
$RG$ is flat as an ![]() $RG_\chi$-module, since the direct sum of flat modules is flat. To this end, let
$RG_\chi$-module, since the direct sum of flat modules is flat. To this end, let ![]() $\iota \colon M \hookrightarrow N$ be an injection of right
$\iota \colon M \hookrightarrow N$ be an injection of right ![]() $RG_\chi$-modules; our goal is to show that
$RG_\chi$-modules; our goal is to show that ![]() $\iota \otimes \operatorname {id} \colon M \otimes _{RG_\chi } RG \rightarrow N \otimes _{RG_\chi } RG$ is injective. Let
$\iota \otimes \operatorname {id} \colon M \otimes _{RG_\chi } RG \rightarrow N \otimes _{RG_\chi } RG$ is injective. Let ![]() $g \in G$ be such that
$g \in G$ be such that ![]() $\chi (g) < 0$ and consider the left
$\chi (g) < 0$ and consider the left ![]() $RG_\chi$-module
$RG_\chi$-module ![]() $RG_\chi g^k = \{ \alpha g^k : \alpha \in RG_\chi, k \in \mathbb {Z} \}$. The modules
$RG_\chi g^k = \{ \alpha g^k : \alpha \in RG_\chi, k \in \mathbb {Z} \}$. The modules ![]() $RG_\chi g^k$ form a directed system with respect to the inclusion maps
$RG_\chi g^k$ form a directed system with respect to the inclusion maps ![]() $RG_\chi g^k \hookrightarrow RG_\chi g^l$ for
$RG_\chi g^k \hookrightarrow RG_\chi g^l$ for ![]() $k \leqslant l$ and the direct limit is
$k \leqslant l$ and the direct limit is ![]() $\varinjlim RG_\chi g^k \cong RG$.
$\varinjlim RG_\chi g^k \cong RG$.
There are left ![]() $RG_\chi$-module isomorphisms
$RG_\chi$-module isomorphisms ![]() $RG_\chi g^k \rightarrow RG_\chi$ given by right multiplication by
$RG_\chi g^k \rightarrow RG_\chi$ given by right multiplication by ![]() $g^{-k}$. Then
$g^{-k}$. Then ![]() $RG_\chi g^k$ is flat over
$RG_\chi g^k$ is flat over ![]() $RG_\chi$, so
$RG_\chi$, so ![]() $M \otimes _{RG_\chi } RG_\chi g^k \rightarrow N \otimes _{RG_\chi } RG_\chi g^k$ is injective for all
$M \otimes _{RG_\chi } RG_\chi g^k \rightarrow N \otimes _{RG_\chi } RG_\chi g^k$ is injective for all ![]() $k \in \mathbb {Z}$. By exactness of the direct limit,
$k \in \mathbb {Z}$. By exactness of the direct limit,
is injective. Since the direct limit commutes with the tensor product, the previous line implies ![]() $\iota \otimes \operatorname {id}_M$ is injective.
$\iota \otimes \operatorname {id}_M$ is injective.
We now return to the proof of Theorem 5.3.
Proof Proof of (1)  $\Leftrightarrow$ (2)
$\Leftrightarrow$ (2)
Let ![]() $g \in G$ be such that
$g \in G$ be such that ![]() $\chi (g) < 0$ and let
$\chi (g) < 0$ and let ![]() $E_k$ be the left
$E_k$ be the left ![]() $RG_\chi$-module
$RG_\chi$-module ![]() $g^k F^v$. We denote the chain complexes
$g^k F^v$. We denote the chain complexes ![]() $F^v_\bullet \rightarrow M \rightarrow 0$ and
$F^v_\bullet \rightarrow M \rightarrow 0$ and ![]() $(E_k)_\bullet \rightarrow M \rightarrow 0$ by
$(E_k)_\bullet \rightarrow M \rightarrow 0$ by ![]() $\widetilde {F}^v$ and
$\widetilde {F}^v$ and ![]() $\widetilde {E}_k$, respectively.
$\widetilde {E}_k$, respectively.
Essential acyclicity in dimension ![]() $j$ is equivalent to the existence of an integer
$j$ is equivalent to the existence of an integer ![]() $D \geqslant 0$ such that the inclusion-induced homomorphism
$D \geqslant 0$ such that the inclusion-induced homomorphism ![]() $H_j(\widetilde {E}_k) \rightarrow H_j(\widetilde {E}_{k+D})$ is the zero map for all
$H_j(\widetilde {E}_k) \rightarrow H_j(\widetilde {E}_{k+D})$ is the zero map for all ![]() $k \in \mathbb {N}$. This in turn is equivalent to
$k \in \mathbb {N}$. This in turn is equivalent to ![]() $\varinjlim \prod _{I} H_j(\widetilde {E}_k) = 0$ for any index set
$\varinjlim \prod _{I} H_j(\widetilde {E}_k) = 0$ for any index set ![]() $I$. Here, for fixed
$I$. Here, for fixed ![]() $I$ and
$I$ and ![]() $j$, the powers
$j$, the powers ![]() $\prod _{I} H_j(\widetilde {E}_k)$ form a directed system with respect to the inclusion-induced maps
$\prod _{I} H_j(\widetilde {E}_k)$ form a directed system with respect to the inclusion-induced maps ![]() $\prod _I H_j(\widetilde {E}_k) \rightarrow \prod _I H_j(\widetilde {E}_l)$ for
$\prod _I H_j(\widetilde {E}_k) \rightarrow \prod _I H_j(\widetilde {E}_l)$ for ![]() $k \leqslant l$. Indeed, if
$k \leqslant l$. Indeed, if ![]() $D \geqslant 0$ is such that
$D \geqslant 0$ is such that ![]() $H_j(\widetilde {E}_k) \rightarrow H_j(\widetilde {E}_{k+D})$ is the zero map, it is clear that the direct limit will be zero. Conversely, let
$H_j(\widetilde {E}_k) \rightarrow H_j(\widetilde {E}_{k+D})$ is the zero map, it is clear that the direct limit will be zero. Conversely, let ![]() $I = Z_j(\widetilde {E}_0) = Z_j(\widetilde {F}^v)$ be the set of
$I = Z_j(\widetilde {E}_0) = Z_j(\widetilde {F}^v)$ be the set of ![]() $j$-cycles of
$j$-cycles of ![]() $\widetilde {F}^v$ and consider the element
$\widetilde {F}^v$ and consider the element ![]() $([x])_{x \in I} \in \prod _I H_j(\widetilde {E}_0)$. Since the direct limit is zero, there is some
$([x])_{x \in I} \in \prod _I H_j(\widetilde {E}_0)$. Since the direct limit is zero, there is some ![]() $D \geqslant 0$ such that
$D \geqslant 0$ such that ![]() $([x])_{x \in I} = 0$ in
$([x])_{x \in I} = 0$ in ![]() $\prod _I H_j(\widetilde {E}_D)$, which means that
$\prod _I H_j(\widetilde {E}_D)$, which means that ![]() $\widetilde {F}^v$ is essentially acyclic in dimension
$\widetilde {F}^v$ is essentially acyclic in dimension ![]() $j$.
$j$.
There is a short exact sequence of chain complexes ![]() $0 \rightarrow M \rightarrow \widetilde {E}_k \rightarrow E_k \rightarrow 0$, where, by abuse of notation,
$0 \rightarrow M \rightarrow \widetilde {E}_k \rightarrow E_k \rightarrow 0$, where, by abuse of notation, ![]() $M$ is a chain complex concentrated in dimension
$M$ is a chain complex concentrated in dimension ![]() $-1$ and
$-1$ and ![]() $E_k$ is the chain complex
$E_k$ is the chain complex ![]() $(E_k)_\bullet \rightarrow 0$ with
$(E_k)_\bullet \rightarrow 0$ with ![]() $(E_k)_0$ in dimension
$(E_k)_0$ in dimension ![]() $0$. The long exact sequence in homology associated to the short exact sequence gives
$0$. The long exact sequence in homology associated to the short exact sequence gives ![]() $H_j(\widetilde {E}_k) \cong H_j(E_k)$ for
$H_j(\widetilde {E}_k) \cong H_j(E_k)$ for ![]() $j \geqslant 1$. The interesting part of the long exact sequence is
$j \geqslant 1$. The interesting part of the long exact sequence is
where ![]() $\delta$ is the connecting homomorphism. By exactness of the direct power and direct limit functors, the sequence
$\delta$ is the connecting homomorphism. By exactness of the direct power and direct limit functors, the sequence
is exact. Then ![]() $\widetilde {F}^v$ is essentially acyclic in dimension
$\widetilde {F}^v$ is essentially acyclic in dimension ![]() $0$ if and only if
$0$ if and only if ![]() $\delta$ induces an injection
$\delta$ induces an injection ![]() $\varinjlim \prod _I H_0(E_k) \rightarrow \prod _I M$ for every
$\varinjlim \prod _I H_0(E_k) \rightarrow \prod _I M$ for every ![]() $I$. Moreover,
$I$. Moreover, ![]() $\widetilde {F}^v$ is essentially acyclic in dimension
$\widetilde {F}^v$ is essentially acyclic in dimension ![]() $-1$ if and only if
$-1$ if and only if ![]() $\delta$ induces a surjection
$\delta$ induces a surjection ![]() $\varinjlim \prod _I H_0(E_k) \rightarrow \prod _I M$ for every
$\varinjlim \prod _I H_0(E_k) \rightarrow \prod _I M$ for every ![]() $I$.
$I$.
By Lemma 5.5, ![]() $F_\bullet \rightarrow M \rightarrow 0$ is a flat resolution of
$F_\bullet \rightarrow M \rightarrow 0$ is a flat resolution of ![]() $M$ by left
$M$ by left ![]() $RG_\chi$-modules, so
$RG_\chi$-modules, so
 \[ \operatorname{Tor}^{RG_\chi}_j \bigg(\prod_I RG_\chi, M \bigg) = H_j\bigg(\bigg(\prod_I RG_\chi \bigg) \otimes_{RG_\chi} F \bigg) \]
\[ \operatorname{Tor}^{RG_\chi}_j \bigg(\prod_I RG_\chi, M \bigg) = H_j\bigg(\bigg(\prod_I RG_\chi \bigg) \otimes_{RG_\chi} F \bigg) \]
and, therefore,
 \[ \operatorname{Tor}^{RG_\chi}_j \bigg(\prod_I RG_\chi, M \bigg) = \varinjlim H_j \bigg(\bigg(\prod_I RG_\chi \bigg) \otimes_{RG_\chi} E_k \bigg), \]
\[ \operatorname{Tor}^{RG_\chi}_j \bigg(\prod_I RG_\chi, M \bigg) = \varinjlim H_j \bigg(\bigg(\prod_I RG_\chi \bigg) \otimes_{RG_\chi} E_k \bigg), \]
as ![]() $F = \varinjlim E_k$ and direct limits commute with tensor products and homology. Since
$F = \varinjlim E_k$ and direct limits commute with tensor products and homology. Since ![]() $(E_k)_j$ is a finitely generated free
$(E_k)_j$ is a finitely generated free ![]() $RG_\chi$-module for
$RG_\chi$-module for ![]() $j \leqslant n$, we have
$j \leqslant n$, we have ![]() $(\prod _I RG_\chi ) \otimes _{RG_\chi } (E_k)_j \cong \prod _I (E_k)_j$. Hence,
$(\prod _I RG_\chi ) \otimes _{RG_\chi } (E_k)_j \cong \prod _I (E_k)_j$. Hence, ![]() $\operatorname {Tor}_j^{RG_\chi }(\prod _I RG_\chi,M) = \varinjlim H_j(\prod _I E_k)$ for
$\operatorname {Tor}_j^{RG_\chi }(\prod _I RG_\chi,M) = \varinjlim H_j(\prod _I E_k)$ for ![]() $j < n$.
$j < n$.
To summarise the work done above, we have ![]() $\widetilde {F}^v$ is essentially acyclic in dimensions
$\widetilde {F}^v$ is essentially acyclic in dimensions ![]() $-1 \leqslant j < n$ if and only if:
$-1 \leqslant j < n$ if and only if:
(a)
 $(\prod _I RG_\chi ) \otimes _{RG_\chi } M \rightarrow \prod _I M$ is surjective if
$(\prod _I RG_\chi ) \otimes _{RG_\chi } M \rightarrow \prod _I M$ is surjective if  $n = 0$; and
$n = 0$; and(b)
 $(\prod _I RG_\chi ) \otimes _{RG_\chi } M \rightarrow \prod _I M$ is an isomorphism and
vanishes for
$(\prod _I RG_\chi ) \otimes _{RG_\chi } M \rightarrow \prod _I M$ is an isomorphism and
vanishes for \[ \operatorname{Tor}_j^{RG_\chi}\bigg(\prod_I RG_\chi,M\bigg) \]
\[ \operatorname{Tor}_j^{RG_\chi}\bigg(\prod_I RG_\chi,M\bigg) \]
 $1 \leqslant j < n$ otherwise.
$1 \leqslant j < n$ otherwise.
Here we have used the general fact that ![]() $\operatorname {Tor}_0^R(A,B) \cong A \otimes _R B$. Together with Lemma 1.1 and Proposition 1.2 of [Reference Bieri and EckmannBE74], parts (a) and (b) are equivalent to
$\operatorname {Tor}_0^R(A,B) \cong A \otimes _R B$. Together with Lemma 1.1 and Proposition 1.2 of [Reference Bieri and EckmannBE74], parts (a) and (b) are equivalent to ![]() $M$ being of type
$M$ being of type ![]() $\mathtt {FP}_n(RG_\chi )$. Thus, we conclude that
$\mathtt {FP}_n(RG_\chi )$. Thus, we conclude that ![]() $[\chi ] \in \Sigma ^m_R(G;M)$ if and only
$[\chi ] \in \Sigma ^m_R(G;M)$ if and only ![]() $\widetilde {F}^v$ is essentially acyclic in dimensions
$\widetilde {F}^v$ is essentially acyclic in dimensions ![]() $j = -1, 0, 1, \ldots, n-1$.
$j = -1, 0, 1, \ldots, n-1$.
6. Agrarian homology and main result
Definition 6.1 (Agrarian groups and  $\mathcal {D}$-homology)
$\mathcal {D}$-homology)
Let ![]() $R$ be a ring. A group
$R$ be a ring. A group ![]() $G$ is agrarian over
$G$ is agrarian over ![]() $R$ if there is a skew-field
$R$ if there is a skew-field ![]() $\mathcal {D}$ and an injective ring homomorphism
$\mathcal {D}$ and an injective ring homomorphism ![]() $R G \hookrightarrow \mathcal {D}$. In this case, we will say that
$R G \hookrightarrow \mathcal {D}$. In this case, we will say that ![]() $G$ is
$G$ is ![]() $\mathcal {D}$-agrarian over
$\mathcal {D}$-agrarian over ![]() $R$ if we wish to specify the skew-field.
$R$ if we wish to specify the skew-field.
If ![]() $G$ is
$G$ is ![]() $\mathcal {D}$-agrarian over
$\mathcal {D}$-agrarian over ![]() $R$, we define its
$R$, we define its ![]() $p$-dimensional
$p$-dimensional ![]() $\mathcal {D}$-homology to be
$\mathcal {D}$-homology to be
where ![]() $R$ is the trivial
$R$ is the trivial ![]() $RG$-module and
$RG$-module and ![]() $\mathcal {D}$ is viewed as a
$\mathcal {D}$ is viewed as a ![]() $\mathcal {D}$-
$\mathcal {D}$-![]() $RG$-bimodule via the embedding
$RG$-bimodule via the embedding ![]() $RG \hookrightarrow \mathcal {D}$. The
$RG \hookrightarrow \mathcal {D}$. The ![]() $p$th
$p$th ![]() $\mathcal {D}$-Betti number of
$\mathcal {D}$-Betti number of ![]() $G$ is then
$G$ is then
Note that ![]() $b_p^{\mathcal {D}}(G)$ is well-defined and integral or infinite, since a module over a skew-field has a well-defined dimension.
$b_p^{\mathcal {D}}(G)$ is well-defined and integral or infinite, since a module over a skew-field has a well-defined dimension.
Remark 6.2 The term ‘agrarian’ was introduced by Kielak in [Reference KielakKie20a] in the case ![]() $R = \mathbb {Z}$. Using strong Hughes-freeness, i.e. condition (
$R = \mathbb {Z}$. Using strong Hughes-freeness, i.e. condition (![]() $2^\prime$) after Definition 2.3, it follows that if
$2^\prime$) after Definition 2.3, it follows that if ![]() $G$ is a locally indicable group and
$G$ is a locally indicable group and ![]() $\mathbb {F}$ is a skew-field such that
$\mathbb {F}$ is a skew-field such that ![]() $\mathcal {D}_{\mathbb {F}G}$ exists, then
$\mathcal {D}_{\mathbb {F}G}$ exists, then ![]() $G$ is
$G$ is ![]() $\mathcal {D}_{\mathbb {F}G}$-agrarian over
$\mathcal {D}_{\mathbb {F}G}$-agrarian over ![]() $\mathbb {F}$. If
$\mathbb {F}$. If ![]() $R$ is a skew-field or an integral domain, then there are no known examples of torsion-free groups that are not agrarian over
$R$ is a skew-field or an integral domain, then there are no known examples of torsion-free groups that are not agrarian over ![]() $R$. For the remainder of the section, we will be interested in the
$R$. For the remainder of the section, we will be interested in the ![]() $\mathcal {D}_{\mathbb {F}G}$-homology of
$\mathcal {D}_{\mathbb {F}G}$-homology of ![]() $G$.
$G$.
In what follows, we will need that ![]() $\mathcal {D}_{\mathbb {F}G}$-Betti numbers have good scaling properties when passing to finite index subgroups. This is analogous to the fact that
$\mathcal {D}_{\mathbb {F}G}$-Betti numbers have good scaling properties when passing to finite index subgroups. This is analogous to the fact that ![]() $\ell ^2$-Betti numbers also scale under passage to finite index subgroups.
$\ell ^2$-Betti numbers also scale under passage to finite index subgroups.
Lemma 6.3 Let ![]() $H$ be a finite index subgroup of
$H$ be a finite index subgroup of ![]() $G$ and let
$G$ and let ![]() $\mathbb {F}$ be a skew-field such that
$\mathbb {F}$ be a skew-field such that ![]() $\mathcal {D}_{\mathbb {F}G}$ exists. Then
$\mathcal {D}_{\mathbb {F}G}$ exists. Then
Proof. It suffices to prove the claim when ![]() $H$ is normal in
$H$ is normal in ![]() $G$. To see this, if
$G$. To see this, if ![]() $H \leqslant G$ is any subgroup of finite index, then there is normal subgroup
$H \leqslant G$ is any subgroup of finite index, then there is normal subgroup ![]() $N \triangleleft G$ of finite index such that
$N \triangleleft G$ of finite index such that ![]() $N \leqslant H \leqslant G$ (we can take
$N \leqslant H \leqslant G$ (we can take ![]() $N$ to be the normal core of
$N$ to be the normal core of ![]() $H$, that is, the intersection of all the conjugates of
$H$, that is, the intersection of all the conjugates of ![]() $H$). Then
$H$). Then
by the claim for normal subgroups.
Assume that ![]() $H$ is a finite index normal subgroup of
$H$ is a finite index normal subgroup of ![]() $G$ and let
$G$ and let ![]() $\{t_1, \ldots, t_n \}$ be a transversal for
$\{t_1, \ldots, t_n \}$ be a transversal for ![]() $H$ in
$H$ in ![]() $G$. By Proposition 2.5(2), we have a
$G$. By Proposition 2.5(2), we have a ![]() $\mathcal {D}_{\mathbb {F}H}$-
$\mathcal {D}_{\mathbb {F}H}$-![]() $\mathbb {F}G$-bimodule isomorphism
$\mathbb {F}G$-bimodule isomorphism ![]() $\mathcal {D}_{\mathbb {F}G} \cong \mathcal {D}_{\mathbb {F}H} \otimes _{\mathbb {F}H} \mathbb {F}G$. Take a free resolution
$\mathcal {D}_{\mathbb {F}G} \cong \mathcal {D}_{\mathbb {F}H} \otimes _{\mathbb {F}H} \mathbb {F}G$. Take a free resolution ![]() $F_\bullet \rightarrow \mathbb {F} \rightarrow 0$ of the trivial left
$F_\bullet \rightarrow \mathbb {F} \rightarrow 0$ of the trivial left ![]() $\mathbb {F}G$-module
$\mathbb {F}G$-module ![]() $\mathbb {F}$; there are chain isomorphisms
$\mathbb {F}$; there are chain isomorphisms
of left ![]() $\mathcal {D}_{\mathbb {F}H}$-modules, so
$\mathcal {D}_{\mathbb {F}H}$-modules, so ![]() $H_p^{\mathcal {D}_{\mathbb {F}G}}(G) \cong H_p^{\mathcal {D}_{\mathbb {F}H}}(H)$ as
$H_p^{\mathcal {D}_{\mathbb {F}G}}(G) \cong H_p^{\mathcal {D}_{\mathbb {F}H}}(H)$ as ![]() $\mathcal {D}_{\mathbb {F}H}$-modules. Therefore,
$\mathcal {D}_{\mathbb {F}H}$-modules. Therefore,
 \begin{align*} b_p^{\mathcal{D}_{\mathbb{F}H}}(H) &= \dim_{\mathcal{D}_{\mathbb{F}H}} H_p^{\mathcal{D}_{\mathbb{F}H}}(H) \\ &= \dim_{\mathcal{D}_{\mathbb{F}H}} H_p^{\mathcal{D}_{\mathbb{F}G}}(G) \\ &= [G : H] \cdot \dim_{\mathcal{D}_{\mathbb{F}G}} H_p^{\mathcal{D}_{\mathbb{F}G}}(G) \\ &= [G : H] \cdot b_p^{\mathcal{D}_{\mathbb{F}G}}(G).\end{align*}
\begin{align*} b_p^{\mathcal{D}_{\mathbb{F}H}}(H) &= \dim_{\mathcal{D}_{\mathbb{F}H}} H_p^{\mathcal{D}_{\mathbb{F}H}}(H) \\ &= \dim_{\mathcal{D}_{\mathbb{F}H}} H_p^{\mathcal{D}_{\mathbb{F}G}}(G) \\ &= [G : H] \cdot \dim_{\mathcal{D}_{\mathbb{F}G}} H_p^{\mathcal{D}_{\mathbb{F}G}}(G) \\ &= [G : H] \cdot b_p^{\mathcal{D}_{\mathbb{F}G}}(G).\end{align*}
In view of Lemma 6.3, if ![]() $G$ is a group with a finite index subgroup
$G$ is a group with a finite index subgroup ![]() $H$ such that
$H$ such that ![]() $\mathcal {D}_{\mathbb {F}H}$ exists, we can define
$\mathcal {D}_{\mathbb {F}H}$ exists, we can define ![]() $b_p^{\mathcal {D}_{\mathbb {F}G}}(G) = b_p^{\mathcal {D}_{\mathbb {F}H}}(H)/[G:H]$. This is an abuse of notation since
$b_p^{\mathcal {D}_{\mathbb {F}G}}(G) = b_p^{\mathcal {D}_{\mathbb {F}H}}(H)/[G:H]$. This is an abuse of notation since ![]() $\mathcal {D}_{\mathbb {F}G}$ might not exist.
$\mathcal {D}_{\mathbb {F}G}$ might not exist.
The following theorem is an analogue of a theorem of Lück which holds for ![]() $\ell ^2$-Betti numbers [Reference LückLüc02, Theorem 7.2].
$\ell ^2$-Betti numbers [Reference LückLüc02, Theorem 7.2].
Theorem 6.4 Let ![]() $1 \rightarrow K \rightarrow G \rightarrow \mathbb {Z} \rightarrow 1$ be a short exact sequence of groups and suppose that
$1 \rightarrow K \rightarrow G \rightarrow \mathbb {Z} \rightarrow 1$ be a short exact sequence of groups and suppose that ![]() $\mathcal {D}_{\mathbb {F}G}$ exists for some skew-field
$\mathcal {D}_{\mathbb {F}G}$ exists for some skew-field ![]() $\mathbb {F}$. If
$\mathbb {F}$. If ![]() $b_p^{\mathcal {D}_{\mathbb {F}K}}(K) < \infty$ for some
$b_p^{\mathcal {D}_{\mathbb {F}K}}(K) < \infty$ for some ![]() $p \geqslant 0$, then
$p \geqslant 0$, then ![]() $b_p^{\mathcal {D}_{\mathbb {F}G}}(G) = 0$.
$b_p^{\mathcal {D}_{\mathbb {F}G}}(G) = 0$.
Proof. Let ![]() $F_\bullet \rightarrow \mathbb {F} \rightarrow 0$ be a free resolution of
$F_\bullet \rightarrow \mathbb {F} \rightarrow 0$ be a free resolution of ![]() $\mathbb {F}$ by left
$\mathbb {F}$ by left ![]() $\mathbb {F} G$-modules. Note that the modules
$\mathbb {F} G$-modules. Note that the modules ![]() $F_j$ are also free left
$F_j$ are also free left ![]() $\mathbb {F}K$-modules and there are chain maps
$\mathbb {F}K$-modules and there are chain maps ![]() $\iota _j \colon \mathcal {D}_{\mathbb {F}K} \otimes _{\mathbb {F}K} F_j \rightarrow \mathcal {D}_{\mathbb {F}G} \otimes _{\mathbb {F}G} F_j$, induced by the inclusion
$\iota _j \colon \mathcal {D}_{\mathbb {F}K} \otimes _{\mathbb {F}K} F_j \rightarrow \mathcal {D}_{\mathbb {F}G} \otimes _{\mathbb {F}G} F_j$, induced by the inclusion ![]() $\mathcal {D}_{\mathbb {F}K} \hookrightarrow \mathcal {D}_{\mathbb {F}G}$. We claim that the maps
$\mathcal {D}_{\mathbb {F}K} \hookrightarrow \mathcal {D}_{\mathbb {F}G}$. We claim that the maps ![]() $\iota _j$ are injective. To see this, it is enough to consider the case where
$\iota _j$ are injective. To see this, it is enough to consider the case where ![]() $F_j = \mathbb {F}G$. Choose
$F_j = \mathbb {F}G$. Choose ![]() $t \in G$ such that
$t \in G$ such that ![]() $\{ t^n : n \in \mathbb {Z} \}$ is a transversal for
$\{ t^n : n \in \mathbb {Z} \}$ is a transversal for ![]() $K \leqslant G$. By Proposition 2.5, there is an embedding
$K \leqslant G$. By Proposition 2.5, there is an embedding ![]() $\bigoplus _{n \in \mathbb {Z}} \mathcal {D}_{\mathbb {F}K} \cdot \varphi (t^n) \hookrightarrow \mathcal {D}_{\mathbb {F}G}$. Since
$\bigoplus _{n \in \mathbb {Z}} \mathcal {D}_{\mathbb {F}K} \cdot \varphi (t^n) \hookrightarrow \mathcal {D}_{\mathbb {F}G}$. Since ![]() $\mathbb {F}G$ is free over
$\mathbb {F}G$ is free over ![]() $\mathbb {F}K$, there is also an isomorphism
$\mathbb {F}K$, there is also an isomorphism ![]() $\mathcal {D}_{\mathbb {F}K} \otimes _{\mathbb {F}K} \mathbb {F}G \cong \bigoplus _{n \in \mathbb {Z}} \mathcal {D}_{\mathbb {F}K} \cdot \varphi (t^n)$ determined by
$\mathcal {D}_{\mathbb {F}K} \otimes _{\mathbb {F}K} \mathbb {F}G \cong \bigoplus _{n \in \mathbb {Z}} \mathcal {D}_{\mathbb {F}K} \cdot \varphi (t^n)$ determined by ![]() $\alpha \otimes t^n \mapsto \alpha \varphi (t^n)$. Then the diagram
$\alpha \otimes t^n \mapsto \alpha \varphi (t^n)$. Then the diagram

of left ![]() $\mathcal {D}_{\mathbb {F}K}$-modules commutes, proving that
$\mathcal {D}_{\mathbb {F}K}$-modules commutes, proving that ![]() $\iota _j$ is an injection. From now on, we will treat the maps
$\iota _j$ is an injection. From now on, we will treat the maps ![]() $\iota _j$ as inclusions.
$\iota _j$ as inclusions.
Consider the following portions of the chain complexes computing ![]() $b_p^{\mathcal {D}_{\mathbb {F}G}}(G)$ and
$b_p^{\mathcal {D}_{\mathbb {F}G}}(G)$ and ![]() $b_p^{\mathcal {D}_{\mathbb {F}K}}(K)$.
$b_p^{\mathcal {D}_{\mathbb {F}K}}(K)$.

Let ![]() $x$ be a cycle in
$x$ be a cycle in ![]() $\mathcal {D}_{\mathbb {F}G} \otimes _{\mathbb {F}G} F_p$. By [Reference Jaikin-ZapirainJZ21, Proposition 2.2(2)],
$\mathcal {D}_{\mathbb {F}G} \otimes _{\mathbb {F}G} F_p$. By [Reference Jaikin-ZapirainJZ21, Proposition 2.2(2)], ![]() $\mathcal {D}_{\mathbb {F}G} \cong \mathrm {Ore}(\mathcal {D}_{\mathbb {F}K} * \mathbb {Z})$, where we are making the identifications
$\mathcal {D}_{\mathbb {F}G} \cong \mathrm {Ore}(\mathcal {D}_{\mathbb {F}K} * \mathbb {Z})$, where we are making the identifications ![]() $\mathcal {D}_{\mathbb {F}K} \otimes _{\mathbb {F}K} \mathbb {F}G \cong \bigoplus _{n \in \mathbb {Z}} \mathcal {D}_{\mathbb {F}K} \cdot \varphi (t^n) \cong \mathcal {D}_{\mathbb {F}K} * \mathbb {Z}$. Hence, there is some nonzero
$\mathcal {D}_{\mathbb {F}K} \otimes _{\mathbb {F}K} \mathbb {F}G \cong \bigoplus _{n \in \mathbb {Z}} \mathcal {D}_{\mathbb {F}K} \cdot \varphi (t^n) \cong \mathcal {D}_{\mathbb {F}K} * \mathbb {Z}$. Hence, there is some nonzero ![]() $a \in \mathcal {D}_{\mathbb {F}K} * \mathbb {Z}$ such that
$a \in \mathcal {D}_{\mathbb {F}K} * \mathbb {Z}$ such that ![]() $ax \in \mathcal {D}_{\mathbb {F}K} \otimes _{\mathbb {F}K} F_p$. Since
$ax \in \mathcal {D}_{\mathbb {F}K} \otimes _{\mathbb {F}K} F_p$. Since ![]() $(\mathcal {D}_{\mathbb {F}K} * \mathbb {Z}) \cdot ax \subseteq Z_p(\mathcal {D}_{\mathbb {F}G} \otimes _{\mathbb {F}G} F_\bullet )$ and
$(\mathcal {D}_{\mathbb {F}K} * \mathbb {Z}) \cdot ax \subseteq Z_p(\mathcal {D}_{\mathbb {F}G} \otimes _{\mathbb {F}G} F_\bullet )$ and ![]() $\iota _{p-1}$ is injective,
$\iota _{p-1}$ is injective, ![]() $(\mathcal {D}_{\mathbb {F}K} * \mathbb {Z}) \cdot ax$ is an infinite-dimensional
$(\mathcal {D}_{\mathbb {F}K} * \mathbb {Z}) \cdot ax$ is an infinite-dimensional ![]() $\mathcal {D}_{\mathbb {F}K}$-subspace of
$\mathcal {D}_{\mathbb {F}K}$-subspace of ![]() $Z_p(\mathcal {D}_{\mathbb {F}K} \otimes _{\mathbb {F}K} F_\bullet )$. Since
$Z_p(\mathcal {D}_{\mathbb {F}K} \otimes _{\mathbb {F}K} F_\bullet )$. Since ![]() $b_p^{\mathcal {D}_{\mathbb {F}K}}(K) < \infty$, there is a nonzero
$b_p^{\mathcal {D}_{\mathbb {F}K}}(K) < \infty$, there is a nonzero ![]() $b \in \mathcal {D}_{\mathbb {F}K} * \mathbb {Z}$ such that
$b \in \mathcal {D}_{\mathbb {F}K} * \mathbb {Z}$ such that ![]() $bax = \partial y$ for some
$bax = \partial y$ for some ![]() $y \in \mathcal {D}_{\mathbb {F}K} \otimes _{\mathbb {F}K} F_{p+1}$. However, then
$y \in \mathcal {D}_{\mathbb {F}K} \otimes _{\mathbb {F}K} F_{p+1}$. However, then ![]() $x = \partial ((ba)^{-1} y)$, so we conclude that
$x = \partial ((ba)^{-1} y)$, so we conclude that ![]() $H_p(\mathcal {D}_{\mathbb {F}G} \otimes _{\mathbb {F}G} F_\bullet ) = 0$.
$H_p(\mathcal {D}_{\mathbb {F}G} \otimes _{\mathbb {F}G} F_\bullet ) = 0$.
For the proof of the main theorem, we will need the following version of a theorem of Bieri and Renz. The details of the proof are given in [Reference Bieri and RenzBR88, Theorem 5.1] in the case ![]() $R = \mathbb {Z}$, though the proof goes through in exactly the same way after replacing the ring
$R = \mathbb {Z}$, though the proof goes through in exactly the same way after replacing the ring ![]() $\mathbb {Z}$ by an arbitrary ring
$\mathbb {Z}$ by an arbitrary ring ![]() $R$.
$R$.
Theorem 6.5 (Bieri–Renz)
Let ![]() $G$ be a finitely generated group and let
$G$ be a finitely generated group and let ![]() $N \triangleleft G$ be a normal subgroup containing the commutator subgroup
$N \triangleleft G$ be a normal subgroup containing the commutator subgroup ![]() $[G,G]$. Let
$[G,G]$. Let ![]() $R$ be a unital ring and let
$R$ be a unital ring and let ![]() $M$ be an
$M$ be an ![]() $RG$-module of type
$RG$-module of type ![]() $\mathtt {FP}_n(RG)$. Then
$\mathtt {FP}_n(RG)$. Then ![]() $M \in \mathtt {FP}_n(RN)$ if and only if
$M \in \mathtt {FP}_n(RN)$ if and only if ![]() $\Sigma _R^n(G;M) \supseteq S(G,N) := \{ [\chi ] \in S(G) : \chi (N) = 0 \}$.
$\Sigma _R^n(G;M) \supseteq S(G,N) := \{ [\chi ] \in S(G) : \chi (N) = 0 \}$.
We will also need the following result due to Kielak and Jaikin-Zapirain. Kielak first proved the result in [Reference KielakKie20c, Theorem 5.2] by giving an explicit construction of the Linnell skew-field ![]() $\mathcal {D}(G)$ when
$\mathcal {D}(G)$ when ![]() $G$ is RFRS. In the appendix to [Reference Jaikin-ZapirainJZ21], Jaikin-Zapirain showed that when
$G$ is RFRS. In the appendix to [Reference Jaikin-ZapirainJZ21], Jaikin-Zapirain showed that when ![]() $G$ is RFRS and
$G$ is RFRS and ![]() $\mathbb {F}$ is any skew-field, then
$\mathbb {F}$ is any skew-field, then ![]() $\mathcal {D}_{\mathbb {F} G}$ exists and admits a completely analogous construction to
$\mathcal {D}_{\mathbb {F} G}$ exists and admits a completely analogous construction to ![]() $\mathcal {D}(G)$ (in fact,
$\mathcal {D}(G)$ (in fact, ![]() $\mathcal {D}(G) = \mathcal {D}_{\mathbb {Q} G}$ for a RFRS group
$\mathcal {D}(G) = \mathcal {D}_{\mathbb {Q} G}$ for a RFRS group ![]() $G$). As a consequence, Kielak's proof of Theorem 6.6 still holds after making the replacements
$G$). As a consequence, Kielak's proof of Theorem 6.6 still holds after making the replacements ![]() $\mathbb {Q} \rightsquigarrow \mathbb {F}$ and
$\mathbb {Q} \rightsquigarrow \mathbb {F}$ and ![]() $\mathcal {D}(G) \rightsquigarrow \mathcal {D}_{\mathbb {F}G}$.
$\mathcal {D}(G) \rightsquigarrow \mathcal {D}_{\mathbb {F}G}$.
Theorem 6.6 (Kielak and Jaikin-Zapirain)
Let ![]() $\mathbb {F}$ be a skew-field,
$\mathbb {F}$ be a skew-field, ![]() $G$ a finitely generated RFRS group, and
$G$ a finitely generated RFRS group, and ![]() $n \in \mathbb {N}$. Let
$n \in \mathbb {N}$. Let ![]() $F_\bullet$ be a chain complex of free
$F_\bullet$ be a chain complex of free ![]() $\mathbb {F} G$-modules with
$\mathbb {F} G$-modules with ![]() $F_p$ is finitely generated and
$F_p$ is finitely generated and ![]() $H_p(\mathcal {D}_{\mathbb {F} G} \otimes _{\mathbb {F} G} F_\bullet ) = 0$ for all
$H_p(\mathcal {D}_{\mathbb {F} G} \otimes _{\mathbb {F} G} F_\bullet ) = 0$ for all ![]() $p \leqslant N$. Then, there exist a finite index subgroup
$p \leqslant N$. Then, there exist a finite index subgroup ![]() $H \leqslant G$ and an open subset
$H \leqslant G$ and an open subset ![]() $U \subseteq S(H)$ such that:
$U \subseteq S(H)$ such that:
(1) the closure of
 $U$ contains
$U$ contains  $S(G)$;
$S(G)$;(2)
 $U$ is invariant under the antipodal map;
$U$ is invariant under the antipodal map;(3)
 $H_p(\widehat {\mathbb {F} H}^\chi \otimes _{\mathbb {F} H} F_\bullet ) = 0$ for every
$H_p(\widehat {\mathbb {F} H}^\chi \otimes _{\mathbb {F} H} F_\bullet ) = 0$ for every  $p \leqslant n$ and every
$p \leqslant n$ and every  $[\chi ] \in U$.
$[\chi ] \in U$.
We are now ready to prove the main theorem.
Theorem 6.7 Let ![]() $\mathbb {F}$ be a skew-field and let
$\mathbb {F}$ be a skew-field and let ![]() $G$ be a virtually RFRS group of type
$G$ be a virtually RFRS group of type ![]() $\mathtt {FP}_n(\mathbb {F})$. Then there is a finite index subgroup
$\mathtt {FP}_n(\mathbb {F})$. Then there is a finite index subgroup ![]() $H \leqslant G$ admitting a homomorphism onto
$H \leqslant G$ admitting a homomorphism onto ![]() $\mathbb {Z}$ with kernel of type
$\mathbb {Z}$ with kernel of type ![]() $\mathtt {FP}_n(\mathbb {F})$ if and only if
$\mathtt {FP}_n(\mathbb {F})$ if and only if ![]() $b_p^{\mathcal {D}_{\mathbb {F}G}}(G) = 0$ for
$b_p^{\mathcal {D}_{\mathbb {F}G}}(G) = 0$ for ![]() $p = 0, \ldots, n$.
$p = 0, \ldots, n$.
Proof. (![]() $\Rightarrow$) Let
$\Rightarrow$) Let ![]() $\varphi \colon H \rightarrow \mathbb {Z}$ be an epimorphism with kernel
$\varphi \colon H \rightarrow \mathbb {Z}$ be an epimorphism with kernel ![]() $K \in \mathtt {FP}_n(\mathbb {F})$. Then there is a free resolution
$K \in \mathtt {FP}_n(\mathbb {F})$. Then there is a free resolution ![]() $F_\bullet \rightarrow \mathbb {F} \rightarrow 0$ of the trivial
$F_\bullet \rightarrow \mathbb {F} \rightarrow 0$ of the trivial ![]() $\mathbb {F}K$-module
$\mathbb {F}K$-module ![]() $\mathbb {F}$ with finitely generated
$\mathbb {F}$ with finitely generated ![]() $n$-skeleton. Therefore,
$n$-skeleton. Therefore,
for ![]() $p \leqslant n$ and we have a short exact sequence
$p \leqslant n$ and we have a short exact sequence ![]() $1 \rightarrow K \rightarrow H \rightarrow \mathbb {Z} \rightarrow 1$, so
$1 \rightarrow K \rightarrow H \rightarrow \mathbb {Z} \rightarrow 1$, so ![]() $b_p^{\mathcal {D}_{\mathbb {F}H}}(H) = 0$ for
$b_p^{\mathcal {D}_{\mathbb {F}H}}(H) = 0$ for ![]() $p \leqslant n$ by Theorem 6.4. Then
$p \leqslant n$ by Theorem 6.4. Then ![]() $b_p^{\mathcal {D}_{\mathbb {F}G}}(G) = 0$ for
$b_p^{\mathcal {D}_{\mathbb {F}G}}(G) = 0$ for ![]() $p \leqslant n$ by Lemma 6.3.
$p \leqslant n$ by Lemma 6.3.
(![]() $\Leftarrow$) The properties of being of type
$\Leftarrow$) The properties of being of type ![]() $\mathtt {FP}_n(\mathbb {F})$ and of having vanishing
$\mathtt {FP}_n(\mathbb {F})$ and of having vanishing ![]() $p$th
$p$th ![]() $\mathcal {D}_{\mathbb {F}G}$-Betti number pass to finite index subgroups. Moreover, the property of being virtually fibred passes to finite index overgroups (the same is, of course, true of any virtual property). Hence, we may assume that
$\mathcal {D}_{\mathbb {F}G}$-Betti number pass to finite index subgroups. Moreover, the property of being virtually fibred passes to finite index overgroups (the same is, of course, true of any virtual property). Hence, we may assume that ![]() $G$ is RFRS and of type
$G$ is RFRS and of type ![]() $\mathtt {FP}_n(\mathbb {F})$. Then
$\mathtt {FP}_n(\mathbb {F})$. Then ![]() $H^1(G; \mathbb {R}) \neq 0$ by Proposition 2.7.
$H^1(G; \mathbb {R}) \neq 0$ by Proposition 2.7.
Since ![]() $G \in \mathtt {FP}_n(\mathbb {F})$, there is a free resolution
$G \in \mathtt {FP}_n(\mathbb {F})$, there is a free resolution ![]() $F_\bullet \rightarrow \mathbb {F} \rightarrow 0$ of the trivial
$F_\bullet \rightarrow \mathbb {F} \rightarrow 0$ of the trivial ![]() $\mathbb {F}G$-module
$\mathbb {F}G$-module ![]() $\mathbb {F}$ with
$\mathbb {F}$ with ![]() $F_p$ finitely generated for
$F_p$ finitely generated for ![]() $p \leqslant n$. By assumption,
$p \leqslant n$. By assumption, ![]() $H_p(\mathcal {D}_{\mathbb {F}G} \otimes _{\mathbb {F}G} F_\bullet ) = 0$ for
$H_p(\mathcal {D}_{\mathbb {F}G} \otimes _{\mathbb {F}G} F_\bullet ) = 0$ for ![]() $p \leqslant n$. By Theorem 6.6, there is a finite index subgroup
$p \leqslant n$. By Theorem 6.6, there is a finite index subgroup ![]() $H \leqslant G$ and an open subset
$H \leqslant G$ and an open subset ![]() $U \subseteq H^1(H;\mathbb {R})$ such that the closure of
$U \subseteq H^1(H;\mathbb {R})$ such that the closure of ![]() $U$ contains
$U$ contains ![]() $H^1(G;\mathbb {R})$, is invariant under nonzero scalar multiplication, and
$H^1(G;\mathbb {R})$, is invariant under nonzero scalar multiplication, and ![]() $H_p(\widehat {\mathbb {F}H}^\varphi \otimes _{\mathbb {F}H} F_\bullet ) = 0$ for
$H_p(\widehat {\mathbb {F}H}^\varphi \otimes _{\mathbb {F}H} F_\bullet ) = 0$ for ![]() $p \leqslant n$ and all
$p \leqslant n$ and all ![]() $\phi \in U$. Since
$\phi \in U$. Since ![]() $U$ is nonempty, we can find a surjective character
$U$ is nonempty, we can find a surjective character ![]() $\varphi \colon H \rightarrow \mathbb {Z}$ in
$\varphi \colon H \rightarrow \mathbb {Z}$ in ![]() $U$. To see this, let
$U$. To see this, let ![]() $\varphi \in H^1(G;\mathbb {R})$ be a nontrivial character. Since
$\varphi \in H^1(G;\mathbb {R})$ be a nontrivial character. Since ![]() $U$ is open,
$U$ is open, ![]() $\varphi$ can be perturbed so that its image is in
$\varphi$ can be perturbed so that its image is in ![]() $\mathbb {Q}$. Finally, since
$\mathbb {Q}$. Finally, since ![]() $H$ is finitely generated, we can rescale the character so that it maps
$H$ is finitely generated, we can rescale the character so that it maps ![]() $H$ onto
$H$ onto ![]() $\mathbb {Z}$. Then
$\mathbb {Z}$. Then ![]() $[\pm \varphi ] \in \Sigma _\mathbb {F}^n(H;\mathbb {F})$ by Theorem 5.3. It is not hard to show that
$[\pm \varphi ] \in \Sigma _\mathbb {F}^n(H;\mathbb {F})$ by Theorem 5.3. It is not hard to show that ![]() $[\chi ] = [\pm \varphi ]$ for any character
$[\chi ] = [\pm \varphi ]$ for any character ![]() $\chi \colon H \rightarrow \mathbb {R}$ with
$\chi \colon H \rightarrow \mathbb {R}$ with ![]() $\ker \varphi \subseteq \ker \chi$. Thus,
$\ker \varphi \subseteq \ker \chi$. Thus, ![]() $\ker \varphi \in \mathtt {FP}_n(\mathbb {F})$ by Theorem 6.5.
$\ker \varphi \in \mathtt {FP}_n(\mathbb {F})$ by Theorem 6.5.
Corollary 6.8 Let ![]() $G$ be virtually RFRS and of type
$G$ be virtually RFRS and of type ![]() $\mathtt {FP}(\mathbb {F})$. Then
$\mathtt {FP}(\mathbb {F})$. Then ![]() $G$ virtually algebraically fibres with kernel of type
$G$ virtually algebraically fibres with kernel of type ![]() $\mathtt {FP}(\mathbb {F})$ if and only if
$\mathtt {FP}(\mathbb {F})$ if and only if ![]() $G$ is
$G$ is ![]() $\mathcal {D}_{\mathbb {F}{G}}$-acyclic.
$\mathcal {D}_{\mathbb {F}{G}}$-acyclic.
Proof. One direction is clear. If ![]() $G$ is
$G$ is ![]() $\mathcal {D}_{\mathbb {F}{G}}$-acyclic, then
$\mathcal {D}_{\mathbb {F}{G}}$-acyclic, then ![]() $G$ virtually algebraically fibres with kernel
$G$ virtually algebraically fibres with kernel ![]() $K$ of type
$K$ of type ![]() $\mathtt {FP}_n(\mathbb {F})$ for
$\mathtt {FP}_n(\mathbb {F})$ for ![]() $n > \operatorname {cd}_\mathbb {F}(G)$. However, then
$n > \operatorname {cd}_\mathbb {F}(G)$. However, then ![]() $n > \operatorname {cd}_\mathbb {F} (K)$, so
$n > \operatorname {cd}_\mathbb {F} (K)$, so ![]() $K$ is of type
$K$ is of type ![]() $\mathtt {FP}(\mathbb {F})$.
$\mathtt {FP}(\mathbb {F})$.
We now apply Theorem 6.7 to the case ![]() $\mathbb {F} = \mathbb {Q}$.
$\mathbb {F} = \mathbb {Q}$.
Definition 6.9 ( $\ell ^2$-Betti numbers)
$\ell ^2$-Betti numbers)
Let ![]() $G$ be a torsion-free group satisfying the Atiyah conjecture and let
$G$ be a torsion-free group satisfying the Atiyah conjecture and let ![]() $\mathcal {D}(G)$ be the Linnell skew-field of
$\mathcal {D}(G)$ be the Linnell skew-field of ![]() $G$ (see the following remark). Define
$G$ (see the following remark). Define
to be the ![]() $p$th
$p$th ![]() $\ell ^2$-Betti number of
$\ell ^2$-Betti number of ![]() $G$.
$G$.
If a group ![]() $G$ has a torsion-free subgroup
$G$ has a torsion-free subgroup ![]() $H$ of finite index satisfying the Atiyah conjecture, we extend the definition of
$H$ of finite index satisfying the Atiyah conjecture, we extend the definition of ![]() $\ell ^2$-Betti numbers by declaring that
$\ell ^2$-Betti numbers by declaring that
 \[ b_n^{(2)}(G) = \frac{b_n^{(2)}(H)}{[G:H]}. \]
\[ b_n^{(2)}(G) = \frac{b_n^{(2)}(H)}{[G:H]}. \]
Remark 6.10 This definition of ![]() $\ell ^2$-Betti numbers for torsion-free groups satisfying the Atiyah conjecture agrees with the usual definition by [Reference LückLüc02, Lemma 10.28(3)]. Moreover,
$\ell ^2$-Betti numbers for torsion-free groups satisfying the Atiyah conjecture agrees with the usual definition by [Reference LückLüc02, Lemma 10.28(3)]. Moreover, ![]() $\ell ^2$-Betti numbers for virtually torsion-free groups are well-defined and coincide with the usual definition by [Reference LückLüc02, Theorem 6.54(6)]. We will not give the definition of the Linnell ring
$\ell ^2$-Betti numbers for virtually torsion-free groups are well-defined and coincide with the usual definition by [Reference LückLüc02, Theorem 6.54(6)]. We will not give the definition of the Linnell ring ![]() $\mathcal {D}(G)$ since that would take us too far afield. We take the Atiyah conjecture to be the statement that
$\mathcal {D}(G)$ since that would take us too far afield. We take the Atiyah conjecture to be the statement that ![]() $\mathcal {D}(G)$ is a skew-field, which allows us to make Definition 6.9. Linnell showed that this formulation implies the strong Atiyah conjecture over
$\mathcal {D}(G)$ is a skew-field, which allows us to make Definition 6.9. Linnell showed that this formulation implies the strong Atiyah conjecture over ![]() $\mathbb {Q}$ for torsion-free groups [Reference LinnellLin93]. The details of the reverse implication can be found in Lück's book [Reference LückLüc02, § 10].
$\mathbb {Q}$ for torsion-free groups [Reference LinnellLin93]. The details of the reverse implication can be found in Lück's book [Reference LückLüc02, § 10].
In the case where ![]() $G$ is finitely generated and RFRS,
$G$ is finitely generated and RFRS, ![]() $\mathcal {D}_{\mathbb {Q} G}$ exists and is isomorphic to the Linnell skew-field
$\mathcal {D}_{\mathbb {Q} G}$ exists and is isomorphic to the Linnell skew-field ![]() $\mathcal {D}(G)$ by Jaikin-Zapirain's appendix to [Reference Jaikin-ZapirainJZ21]. Then, the
$\mathcal {D}(G)$ by Jaikin-Zapirain's appendix to [Reference Jaikin-ZapirainJZ21]. Then, the ![]() $\ell ^2$-Betti numbers of
$\ell ^2$-Betti numbers of ![]() $G$ are defined and
$G$ are defined and ![]() $b_p^{(2)}(G) = b_p^{\mathcal {D}_{\mathbb {Q} G}}(G)$. Hence, applying Theorem 6.7 to the case
$b_p^{(2)}(G) = b_p^{\mathcal {D}_{\mathbb {Q} G}}(G)$. Hence, applying Theorem 6.7 to the case ![]() $\mathbb {F} = \mathbb {Q}$ yields the following result stated in the introduction.
$\mathbb {F} = \mathbb {Q}$ yields the following result stated in the introduction.
Theorem 6.11 Let ![]() $G$ be a virtually RFRS group of type
$G$ be a virtually RFRS group of type ![]() $\mathtt {FP}_n(\mathbb {Q})$. Then there is a finite index subgroup
$\mathtt {FP}_n(\mathbb {Q})$. Then there is a finite index subgroup ![]() $H \leqslant G$ admitting a homomorphism onto
$H \leqslant G$ admitting a homomorphism onto ![]() $\mathbb {Z}$ with kernel of type
$\mathbb {Z}$ with kernel of type ![]() $\mathtt {FP}_n(\mathbb {Q})$ if and only if
$\mathtt {FP}_n(\mathbb {Q})$ if and only if ![]() $b_p^{(2)}(G) = 0$ for
$b_p^{(2)}(G) = 0$ for ![]() $p = 0, \ldots, n$.
$p = 0, \ldots, n$.
Thanks to Jaikin-Zapirain's work on rank functions in [Reference Jaikin-ZapirainJZ21], we can give a third characterisation of algebraic fibring. First, we set up some notation and terminology. If ![]() $R$ is a ring and
$R$ is a ring and ![]() $\varphi \colon R \rightarrow \mathcal {D}$ is a division
$\varphi \colon R \rightarrow \mathcal {D}$ is a division ![]() $R$-ring, then there is a natural rank function on matrices over
$R$-ring, then there is a natural rank function on matrices over ![]() $R$, which we denote
$R$, which we denote ![]() $\operatorname {rk}_{\mathcal {D}, \varphi }$ or simply
$\operatorname {rk}_{\mathcal {D}, \varphi }$ or simply ![]() $\operatorname {rk}_{\mathcal {D}}$ when the map
$\operatorname {rk}_{\mathcal {D}}$ when the map ![]() $\varphi$ is understood. If
$\varphi$ is understood. If ![]() $\varphi$ is epic, meaning that
$\varphi$ is epic, meaning that ![]() $\varphi (R)$ generates
$\varphi (R)$ generates ![]() $\mathcal {D}$ as a division ring, then we call
$\mathcal {D}$ as a division ring, then we call ![]() $\mathcal {D}$ universal if the
$\mathcal {D}$ universal if the ![]() $\operatorname {rk}_\mathcal {D} \geqslant \operatorname {rk}_\mathcal {E}$ for every division
$\operatorname {rk}_\mathcal {D} \geqslant \operatorname {rk}_\mathcal {E}$ for every division ![]() $R$-ring
$R$-ring ![]() $\psi \colon R \rightarrow \mathcal {E}$. Note that if a universal division
$\psi \colon R \rightarrow \mathcal {E}$. Note that if a universal division ![]() $R$-ring exists, then it is unique up to
$R$-ring exists, then it is unique up to ![]() $R$-isomorphism by a result of Cohn [Reference CohnCoh95, Theorem 4.4.1]. If, additionally,
$R$-isomorphism by a result of Cohn [Reference CohnCoh95, Theorem 4.4.1]. If, additionally, ![]() $\varphi$ is an injection, then we call
$\varphi$ is an injection, then we call ![]() $\mathcal {D}$ the universal division ring of fractions for
$\mathcal {D}$ the universal division ring of fractions for ![]() $R$.
$R$.
Theorem 6.12 (Jaikin-Zapirain [Reference Jaikin-ZapirainJZ21, Corollary 1.3])
If ![]() $G$ is a residually (locally indicable and amenable) group and
$G$ is a residually (locally indicable and amenable) group and ![]() $\mathbb {F}$ is a skew-field, then the Hughes-free division ring
$\mathbb {F}$ is a skew-field, then the Hughes-free division ring ![]() $\mathcal {D}_{\mathbb {F}{G}}$ exists and is the universal division ring of fractions for
$\mathcal {D}_{\mathbb {F}{G}}$ exists and is the universal division ring of fractions for ![]() $\mathbb {F}G$.
$\mathbb {F}G$.
Following Jaikin-Zapirain, whenever ![]() $G$ has a Hughes-free division ring
$G$ has a Hughes-free division ring ![]() $\mathcal {D}_{\mathbb {F}{G}}$, we denote the rank function
$\mathcal {D}_{\mathbb {F}{G}}$, we denote the rank function ![]() $\operatorname {rk}_{\mathcal {D}_{\mathbb {F}{G}}}$ by
$\operatorname {rk}_{\mathcal {D}_{\mathbb {F}{G}}}$ by ![]() $\operatorname {rk}_{\mathbb {F}G}$. Note, in particular, that Theorem 6.12 holds for RFRS groups since they are residually poly-
$\operatorname {rk}_{\mathbb {F}G}$. Note, in particular, that Theorem 6.12 holds for RFRS groups since they are residually poly-![]() $\mathbb {Z}$ (see, e.g., [Reference Jaikin-ZapirainJZ21, Proposition 4.4]). Therefore, we have the following corollary, which will be useful to us later.
$\mathbb {Z}$ (see, e.g., [Reference Jaikin-ZapirainJZ21, Proposition 4.4]). Therefore, we have the following corollary, which will be useful to us later.
Corollary 6.13 Let ![]() $G$ be a RFRS group and let
$G$ be a RFRS group and let ![]() $\varphi \colon G \rightarrow \mathbb {Z}$ be a homomorphism. Let
$\varphi \colon G \rightarrow \mathbb {Z}$ be a homomorphism. Let ![]() $A$ be a matrix over
$A$ be a matrix over ![]() $\mathbb {F}G$ and let
$\mathbb {F}G$ and let ![]() $A^\mathbb {Z}$ be the matrix over
$A^\mathbb {Z}$ be the matrix over ![]() $\mathbb {F}[\mathbb {Z}]$ obtained by applying
$\mathbb {F}[\mathbb {Z}]$ obtained by applying ![]() $\varphi$ to
$\varphi$ to ![]() $A$. Then
$A$. Then ![]() $\operatorname {rk}_{\mathbb {F}G} A \geqslant \operatorname {rk}_{\mathbb {F}[\mathbb {Z}]} A^\mathbb {Z}$.
$\operatorname {rk}_{\mathbb {F}G} A \geqslant \operatorname {rk}_{\mathbb {F}[\mathbb {Z}]} A^\mathbb {Z}$.
Proof. There is a map ![]() $\overline {\varphi } \colon \mathbb {F} G \rightarrow \mathbb {F}[\mathbb {Z}] \hookrightarrow \mathcal {D}_{\mathbb {F}{[\mathbb {Z}]}}$ induced by
$\overline {\varphi } \colon \mathbb {F} G \rightarrow \mathbb {F}[\mathbb {Z}] \hookrightarrow \mathcal {D}_{\mathbb {F}{[\mathbb {Z}]}}$ induced by ![]() $\varphi$ and, therefore,
$\varphi$ and, therefore, ![]() $\operatorname {rk}_{\mathbb {F}G} A \geqslant \operatorname {rk}_{\mathcal {D}_{\mathbb {F}{[\mathbb {Z}]}}, \overline {\varphi }} A = \operatorname {rk}_{\mathbb {F}[\mathbb {Z}]} A^\mathbb {Z}$ by universality of
$\operatorname {rk}_{\mathbb {F}G} A \geqslant \operatorname {rk}_{\mathcal {D}_{\mathbb {F}{[\mathbb {Z}]}}, \overline {\varphi }} A = \operatorname {rk}_{\mathbb {F}[\mathbb {Z}]} A^\mathbb {Z}$ by universality of ![]() $\mathcal {D}_{\mathbb {F}{G}}$.
$\mathcal {D}_{\mathbb {F}{G}}$.
The following theorem generalises Corollary 1.5 of [Reference Jaikin-ZapirainJZ21], where the result is proven for ![]() $n = 1$. In the proof, if
$n = 1$. In the proof, if ![]() $M$ is a finitely generated
$M$ is a finitely generated ![]() $\mathbb {F}[\mathbb {Z}]$-module, then we define
$\mathbb {F}[\mathbb {Z}]$-module, then we define ![]() $\dim M := \dim _{\mathcal {D}_{\mathbb {F}{[\mathbb {Z}]}}} (M \otimes _{\mathbb {F}[\mathbb {Z}]} \mathcal {D}_{\mathbb {F}{[\mathbb {Z}]}})$. We will also write
$\dim M := \dim _{\mathcal {D}_{\mathbb {F}{[\mathbb {Z}]}}} (M \otimes _{\mathbb {F}[\mathbb {Z}]} \mathcal {D}_{\mathbb {F}{[\mathbb {Z}]}})$. We will also write ![]() $\operatorname {rk}_G$ instead of
$\operatorname {rk}_G$ instead of ![]() $\operatorname {rk}_{\mathbb {F}G}$ to lighten the notation.
$\operatorname {rk}_{\mathbb {F}G}$ to lighten the notation.
Theorem 6.14 Let ![]() $\mathbb {F}$ be a skew-field and let
$\mathbb {F}$ be a skew-field and let ![]() $G$ be a virtually RFRS group of type
$G$ be a virtually RFRS group of type ![]() $\mathtt {FP}_n(\mathbb {F})$. The following are equivalent:
$\mathtt {FP}_n(\mathbb {F})$. The following are equivalent:
(1) there is a finite index subgroup
 $H_0 \leqslant G$ and a surjection
$H_0 \leqslant G$ and a surjection  $\varphi _0 \colon H_0 \rightarrow \mathbb {Z}$ with
$\varphi _0 \colon H_0 \rightarrow \mathbb {Z}$ with  $\ker \varphi _0$ of type
$\ker \varphi _0$ of type  $\mathtt {FP}_n(\mathbb {F})$;
$\mathtt {FP}_n(\mathbb {F})$;(2) there is a finite index subgroup
 $H_1 \leqslant G$ and a surjection
$H_1 \leqslant G$ and a surjection  $\varphi _1 \colon H_1 \rightarrow \mathbb {Z}$ with
$\varphi _1 \colon H_1 \rightarrow \mathbb {Z}$ with  $b_p(\ker \varphi _1; \mathbb {F}) < \infty$ for
$b_p(\ker \varphi _1; \mathbb {F}) < \infty$ for  $p = 0, \ldots, n$.
$p = 0, \ldots, n$.
Proof. If ![]() $G$ algebraically fibres with kernel
$G$ algebraically fibres with kernel ![]() $K$ of type
$K$ of type ![]() $\mathtt {FP}_n(\mathbb {F})$, then there is a free resolution
$\mathtt {FP}_n(\mathbb {F})$, then there is a free resolution ![]() $F_\bullet \rightarrow \mathbb {F} \rightarrow 0$ of the trivial
$F_\bullet \rightarrow \mathbb {F} \rightarrow 0$ of the trivial ![]() $\mathbb {F} K$ module
$\mathbb {F} K$ module ![]() $\mathbb {F}$ such that
$\mathbb {F}$ such that ![]() $F_p$ is finitely generated for all
$F_p$ is finitely generated for all ![]() $p \leqslant n$. This resolution can be used to compute the homology of
$p \leqslant n$. This resolution can be used to compute the homology of ![]() $K$ and, therefore,
$K$ and, therefore, ![]() $b_p(K; \mathbb {F}) < \infty$ for all
$b_p(K; \mathbb {F}) < \infty$ for all ![]() $p \leqslant n$.
$p \leqslant n$.
In view of Theorem 6.7, to prove the converse it suffices to show that ![]() $b_p^{\mathcal {D}_{\mathbb {F}{G}}}(G) = 0$ for all
$b_p^{\mathcal {D}_{\mathbb {F}{G}}}(G) = 0$ for all ![]() $p \leqslant n$. By multiplicativity of
$p \leqslant n$. By multiplicativity of ![]() $\mathcal {D}_{\mathbb {F}{G}}$-Betti numbers (Lemma 6.3), we may assume that
$\mathcal {D}_{\mathbb {F}{G}}$-Betti numbers (Lemma 6.3), we may assume that ![]() $H_1 = G$. Let
$H_1 = G$. Let ![]() $K = \ker \varphi _1$ and write
$K = \ker \varphi _1$ and write ![]() $\mathbb {F}[\mathbb {Z}]$ for the group algebra
$\mathbb {F}[\mathbb {Z}]$ for the group algebra ![]() $\mathbb {F}[G/K]$. Moreover, note that
$\mathbb {F}[G/K]$. Moreover, note that ![]() $H_p(K;\mathbb {F}) \cong H_p(G; \mathbb {F}[\mathbb {Z}])$ for all
$H_p(K;\mathbb {F}) \cong H_p(G; \mathbb {F}[\mathbb {Z}])$ for all ![]() $p$. Let
$p$. Let
be a free resolution of the trivial ![]() $\mathbb {F} G$-module
$\mathbb {F} G$-module ![]() $\mathbb {F}$, where
$\mathbb {F}$, where ![]() $d_p$ is some cardinal for each
$d_p$ is some cardinal for each ![]() $p$ and
$p$ and ![]() $d_p$ is finite for each
$d_p$ is finite for each ![]() $p \leqslant n$, and we use the (non-standard) notation
$p \leqslant n$, and we use the (non-standard) notation ![]() $\mathbb {F} G^{d_p}$ to denote the
$\mathbb {F} G^{d_p}$ to denote the ![]() $d_p$-fold direct sum of
$d_p$-fold direct sum of ![]() $\mathbb {F} G$, as opposed to the
$\mathbb {F} G$, as opposed to the ![]() $d_p$-fold direct product. The quotient map
$d_p$-fold direct product. The quotient map ![]() $G \rightarrow \mathbb {Z}$ induces a chain map
$G \rightarrow \mathbb {Z}$ induces a chain map

where the boundary maps are viewed as matrices and ![]() $\partial _p^\mathbb {Z}$ is obtained by applying the map
$\partial _p^\mathbb {Z}$ is obtained by applying the map ![]() $G \rightarrow \mathbb {Z}$ to each entry of the matrix
$G \rightarrow \mathbb {Z}$ to each entry of the matrix ![]() $\partial _p$. Note that the homology of the bottom chain complex is
$\partial _p$. Note that the homology of the bottom chain complex is ![]() $H_\bullet (G;\mathbb {Q}[\mathbb {Z}])$.
$H_\bullet (G;\mathbb {Q}[\mathbb {Z}])$.
To apply Jaikin-Zapirain's results on rank functions, we will need the boundary maps to be between finitely generated free modules. However, ![]() $d_{n+1}$ is not finite in general, so we must modify the chain complexes as follows. Since
$d_{n+1}$ is not finite in general, so we must modify the chain complexes as follows. Since ![]() $\mathbb {F}[\mathbb {Z}]$ is Noetherian and
$\mathbb {F}[\mathbb {Z}]$ is Noetherian and ![]() $\mathbb {F}[\mathbb {Z}]^{d_n}$ is finitely generated,
$\mathbb {F}[\mathbb {Z}]^{d_n}$ is finitely generated, ![]() $\operatorname {im} \partial _{n+1}^\mathbb {Z}$ is a finitely generated submodule of
$\operatorname {im} \partial _{n+1}^\mathbb {Z}$ is a finitely generated submodule of ![]() $\mathbb {F}[\mathbb {Z}]^{d_n}$. The preimage of a finite generating set of
$\mathbb {F}[\mathbb {Z}]^{d_n}$. The preimage of a finite generating set of ![]() $\operatorname {im} \partial _{n+1}^\mathbb {Z}$ is contained in a finitely generated free summand
$\operatorname {im} \partial _{n+1}^\mathbb {Z}$ is contained in a finitely generated free summand ![]() $F$ of
$F$ of ![]() $\mathbb {F}[\mathbb {Z}]^{d_{n+1}}$. Note that the homology of
$\mathbb {F}[\mathbb {Z}]^{d_{n+1}}$. Note that the homology of
is still ![]() $H_p(G; \mathbb {F}[\mathbb {Z}])$ for
$H_p(G; \mathbb {F}[\mathbb {Z}])$ for ![]() $p \leqslant n$. The preimage of
$p \leqslant n$. The preimage of ![]() $F$ in
$F$ in ![]() $\mathbb {F} G^{d_{n+1}}$ is again a finitely generated free summand
$\mathbb {F} G^{d_{n+1}}$ is again a finitely generated free summand ![]() $\widehat {F}$ of
$\widehat {F}$ of ![]() $\mathbb {F} G^{d_{n+1}}$. Note that it suffices to show that the homology of
$\mathbb {F} G^{d_{n+1}}$. Note that it suffices to show that the homology of
vanishes in degrees ![]() $\leqslant n$ to show that
$\leqslant n$ to show that ![]() $b_p^{\mathcal {D}_{\mathbb {F}{G}}}(G) = 0$ for all
$b_p^{\mathcal {D}_{\mathbb {F}{G}}}(G) = 0$ for all ![]() $p \leqslant n$.
$p \leqslant n$.
We assume that ![]() $d_{n+1}$ is finite and that
$d_{n+1}$ is finite and that ![]() $F = \mathbb {F}[\mathbb {Z}]^{d_{n+1}}$ and
$F = \mathbb {F}[\mathbb {Z}]^{d_{n+1}}$ and ![]() $\widehat {F} = \mathbb {F} G^{d_{n+1}}$. Since, for every
$\widehat {F} = \mathbb {F} G^{d_{n+1}}$. Since, for every ![]() $p \leqslant n$, the homology
$p \leqslant n$, the homology ![]() $H_p(G;\mathbb {F}[\mathbb {Z}])$ is finite-dimensional as an
$H_p(G;\mathbb {F}[\mathbb {Z}])$ is finite-dimensional as an ![]() $\mathbb {F}$-vector space, it must be torsion as an
$\mathbb {F}$-vector space, it must be torsion as an ![]() $\mathbb {F}[\mathbb {Z}]$-module. Therefore,
$\mathbb {F}[\mathbb {Z}]$-module. Therefore, ![]() $\operatorname {rk}_\mathbb {Z} \partial _{p+1}^\mathbb {Z} = \dim \ker \partial _p^\mathbb {Z}$ for every
$\operatorname {rk}_\mathbb {Z} \partial _{p+1}^\mathbb {Z} = \dim \ker \partial _p^\mathbb {Z}$ for every ![]() $p \leqslant n$. Now, for each
$p \leqslant n$. Now, for each ![]() $p \leqslant n$, we have short exact sequences
$p \leqslant n$, we have short exact sequences
which implies that ![]() $d_p = \dim \ker \partial _p^\mathbb {Z} + \operatorname {rk}_\mathbb {Z} \partial _p^\mathbb {Z} = \operatorname {rk}_\mathbb {Z} \partial _{p+1}^\mathbb {Z} + \operatorname {rk}_\mathbb {Z} \partial _p^\mathbb {Z}$. Hence,
$d_p = \dim \ker \partial _p^\mathbb {Z} + \operatorname {rk}_\mathbb {Z} \partial _p^\mathbb {Z} = \operatorname {rk}_\mathbb {Z} \partial _{p+1}^\mathbb {Z} + \operatorname {rk}_\mathbb {Z} \partial _p^\mathbb {Z}$. Hence,
 \begin{align*} d_p - \operatorname{rk}_G \partial_p &= \dim_{\mathcal{D}_{\mathbb{F}{G}}} \ker(\mathcal{D}_{\mathbb{F}{G}}^{d_p} \xrightarrow{\partial_p} \mathcal{D}_{\mathbb{F}{G}}^{d_{p-1}} ) \\ &\geqslant \operatorname{rk}_G \partial_{p+1} \\ &\geqslant \operatorname{rk}_\mathbb{Z} \partial_{p+1}^\mathbb{Z} \\ &= d_p - \operatorname{rk}_\mathbb{Z} \partial_p^\mathbb{Z} \\ &\geqslant d_p - \operatorname{rk}_G \partial_p, \end{align*}
\begin{align*} d_p - \operatorname{rk}_G \partial_p &= \dim_{\mathcal{D}_{\mathbb{F}{G}}} \ker(\mathcal{D}_{\mathbb{F}{G}}^{d_p} \xrightarrow{\partial_p} \mathcal{D}_{\mathbb{F}{G}}^{d_{p-1}} ) \\ &\geqslant \operatorname{rk}_G \partial_{p+1} \\ &\geqslant \operatorname{rk}_\mathbb{Z} \partial_{p+1}^\mathbb{Z} \\ &= d_p - \operatorname{rk}_\mathbb{Z} \partial_p^\mathbb{Z} \\ &\geqslant d_p - \operatorname{rk}_G \partial_p, \end{align*}
where we have used Corollary 6.13. Thus,
and therefore ![]() $b_p^{\mathcal {D}_{\mathbb {F}{G}}}(G) = 0$ for all
$b_p^{\mathcal {D}_{\mathbb {F}{G}}}(G) = 0$ for all ![]() $p \leqslant n$.
$p \leqslant n$.
Corollary 6.15 Let ![]() $G$ be a virtually RFRS group and let
$G$ be a virtually RFRS group and let ![]() $n \in \mathbb {N}$.
$n \in \mathbb {N}$.
(1) If
 $\mathbb {F}$ and
$\mathbb {F}$ and  $\mathbb {F}'$ are skew-fields of the same characteristic, then
$\mathbb {F}'$ are skew-fields of the same characteristic, then  $G$ virtually algebraically fibres with kernel of type
$G$ virtually algebraically fibres with kernel of type  $\mathtt {FP}_n(\mathbb {F})$ if and only if it virtually algebraically fibres with kernel of type
$\mathtt {FP}_n(\mathbb {F})$ if and only if it virtually algebraically fibres with kernel of type  $\mathtt {FP}_n(\mathbb {F}')$.
$\mathtt {FP}_n(\mathbb {F}')$.(2) If
 $p$ is a prime such that
$p$ is a prime such that  $G$ algebraically fibres with kernel of type
$G$ algebraically fibres with kernel of type  $\mathtt {FP}_n(\mathbb {F}_p)$, then it fibres with kernel of type
$\mathtt {FP}_n(\mathbb {F}_p)$, then it fibres with kernel of type  $\mathtt {FP}_n(\mathbb {Q})$.
$\mathtt {FP}_n(\mathbb {Q})$.
Proof. Item (1) follows from the fact that the Betti numbers of a group with trivial skew-field coefficients depend only on the characteristic of the skew-field. Item (2) follows from the fact that ![]() $b_k(G; \mathbb {F}_p) \geqslant b_k(G; \mathbb {Q})$ for any group
$b_k(G; \mathbb {F}_p) \geqslant b_k(G; \mathbb {Q})$ for any group ![]() $G$ and any prime
$G$ and any prime ![]() $p$ (this is a consequence of the universal coefficient theorem).
$p$ (this is a consequence of the universal coefficient theorem).
7. Applications
7.1 Amenable RFRS groups
Definition 7.1 A group ![]() $G$ is amenable if for every continuous
$G$ is amenable if for every continuous ![]() $G$-action on a compact, Hausdorff space
$G$-action on a compact, Hausdorff space ![]() $X$, there is a
$X$, there is a ![]() $G$-invariant probability measure on
$G$-invariant probability measure on ![]() $X$.
$X$.
Definition 7.2 (Elementary amenable groups)
The class ![]() $\mathcal {E}$ of elementary amenable groups is the smallest class such that:
$\mathcal {E}$ of elementary amenable groups is the smallest class such that:
•
 $\mathcal {E}$ contains all finite groups and all Abelian groups;
$\mathcal {E}$ contains all finite groups and all Abelian groups;• if
 $G \in \mathcal {E}$ then the entire isomorphism class of
$G \in \mathcal {E}$ then the entire isomorphism class of  $G$ is contained in
$G$ is contained in  $\mathcal {E}$;
$\mathcal {E}$;•
 $\mathcal {E}$ is closed under taking subgroups, quotients, extensions, and directed unions.
$\mathcal {E}$ is closed under taking subgroups, quotients, extensions, and directed unions.
All elementary amenable groups are amenable, however there are many examples of amenable groups that are not elementary amenable, the earliest being Grigorchuk's group of intermediate growth [Reference GrigorčukGri80]. For a discussion of more examples, we refer the reader to the introduction of Juschenko's paper [Reference JuschenkoJus18]. The known examples of non-elementary amenable groups all have infinite cohomological dimension over any field. Moreover, elementary amenable groups of finite cohomological dimension over ![]() $\mathbb {Z}$ are virtually solvable by [Reference HillmanHil91, Lemma 2] and [Reference Hillman and LinnellHL92, Corollary 1]. We are led to the following question, which was stated in the introduction.
$\mathbb {Z}$ are virtually solvable by [Reference HillmanHil91, Lemma 2] and [Reference Hillman and LinnellHL92, Corollary 1]. We are led to the following question, which was stated in the introduction.
Question 7.3 Are amenable groups of finite cohomological dimension over ![]() $\mathbb {Z}$ virtually solvable?
$\mathbb {Z}$ virtually solvable?
We obtain a partial answer in the positive direction as an application of Theorem 6.11, and extends the well-known fact that nilpotent RFRS groups are Abelian. The author thanks Sami Douba for pointing out the fact (and the proof) that polycyclic RFRS groups are virtually Abelian, which allows us to strengthen the following theorem.
Theorem 7.4 If ![]() $G$ is an amenable RFRS group of type
$G$ is an amenable RFRS group of type ![]() $\mathtt {FP}(\mathbb {Q})$, then
$\mathtt {FP}(\mathbb {Q})$, then ![]() $G$ is virtually Abelian.
$G$ is virtually Abelian.
Proof. Since ![]() $G$ is amenable,
$G$ is amenable, ![]() $b_p^{\mathcal {D}_{\mathbb {Q} G}}(G) = 0$ for all
$b_p^{\mathcal {D}_{\mathbb {Q} G}}(G) = 0$ for all ![]() $p$ by [Reference LückLüc02, Theorem 7.2(1)]. By Theorem 6.11 we obtain a finite index subgroup
$p$ by [Reference LückLüc02, Theorem 7.2(1)]. By Theorem 6.11 we obtain a finite index subgroup ![]() $H \leqslant G$ and an epimorphism
$H \leqslant G$ and an epimorphism ![]() $\varphi \colon H \rightarrow \mathbb {Z}$ such that
$\varphi \colon H \rightarrow \mathbb {Z}$ such that ![]() $N = \ker \varphi \in \mathtt {FP}_n(\mathbb {Q})$. It will be necessary to require that
$N = \ker \varphi \in \mathtt {FP}_n(\mathbb {Q})$. It will be necessary to require that ![]() $H$ be normal in
$H$ be normal in ![]() $G$, which is not an issue since we can replace
$G$, which is not an issue since we can replace ![]() $H$ with its normal core. Since
$H$ with its normal core. Since ![]() $\operatorname {cd}_{\mathbb {Q}} N \leqslant \operatorname {cd}_\mathbb {Q} G \leqslant n$, we also have
$\operatorname {cd}_{\mathbb {Q}} N \leqslant \operatorname {cd}_\mathbb {Q} G \leqslant n$, we also have ![]() $N \in \mathtt {FP}(\mathbb {Q})$ (see [Reference BrownBro94, Proposition VIII.6.1]). Because we have a short exact sequence
$N \in \mathtt {FP}(\mathbb {Q})$ (see [Reference BrownBro94, Proposition VIII.6.1]). Because we have a short exact sequence
with ![]() $N \in \mathtt {FP}(\mathbb {Q})$, a theorem of Fel'dman [Reference Fel'dmanFel71, Theorem 2.4] (see also [Reference BieriBie76, Proposition 2.5]) gives
$N \in \mathtt {FP}(\mathbb {Q})$, a theorem of Fel'dman [Reference Fel'dmanFel71, Theorem 2.4] (see also [Reference BieriBie76, Proposition 2.5]) gives ![]() $\operatorname {cd}_\mathbb {Q} N = \operatorname {cd}_\mathbb {Q} H - \operatorname {cd}_\mathbb {Q} \mathbb {Z} = n - 1$.
$\operatorname {cd}_\mathbb {Q} N = \operatorname {cd}_\mathbb {Q} H - \operatorname {cd}_\mathbb {Q} \mathbb {Z} = n - 1$.
Since subgroups of amenable RFRS groups are amenable and RFRS, we can repeat the argument above with ![]() $N$ instead of
$N$ instead of ![]() $G$. Iterating this process, we obtain a subnormal series
$G$. Iterating this process, we obtain a subnormal series
of ![]() $G$ such that
$G$ such that ![]() $\operatorname {cd}_\mathbb {Q} G_j = j$ for each
$\operatorname {cd}_\mathbb {Q} G_j = j$ for each ![]() $j$ (note that
$j$ (note that ![]() $N = G_{n-1}$ here). However, the only torsion-free group of cohomological dimension
$N = G_{n-1}$ here). However, the only torsion-free group of cohomological dimension ![]() $0$ over
$0$ over ![]() $\mathbb {Q}$ is the trivial group, so we conclude that
$\mathbb {Q}$ is the trivial group, so we conclude that ![]() $G$ is polycyclic-by-finite.
$G$ is polycyclic-by-finite.
Let ![]() $G' \leqslant G$ be a polycyclic group of finite index. We will show, by induction on the Hirsch length of
$G' \leqslant G$ be a polycyclic group of finite index. We will show, by induction on the Hirsch length of ![]() $G'$, that
$G'$, that ![]() $G'$ must be virtually Abelian. Indeed, by induction we may assume that
$G'$ must be virtually Abelian. Indeed, by induction we may assume that ![]() $G' \cong \mathbb {Z}^m \rtimes _\psi \mathbb {Z}$. If
$G' \cong \mathbb {Z}^m \rtimes _\psi \mathbb {Z}$. If ![]() $\psi$ is of finite order, then
$\psi$ is of finite order, then ![]() $G'$ is virtually Abelian. If
$G'$ is virtually Abelian. If ![]() $\psi$ is of infinite order, then the argument of [Reference Bridson and HaefligerBH99, Proposition 4.17] shows that
$\psi$ is of infinite order, then the argument of [Reference Bridson and HaefligerBH99, Proposition 4.17] shows that ![]() $\mathbb {Z}^m$ cannot be quasi-isometrically embedded in
$\mathbb {Z}^m$ cannot be quasi-isometrically embedded in ![]() $G'$. However, Proposition 2.7(2) implies that all Abelian subgroups of a finitely generated RFRS group are undistorted, a contradiction.
$G'$. However, Proposition 2.7(2) implies that all Abelian subgroups of a finitely generated RFRS group are undistorted, a contradiction.
Remark 7.5 The assumption that ![]() $G$ be RFRS is necessary. For example, the Baumslag–Solitar group
$G$ be RFRS is necessary. For example, the Baumslag–Solitar group ![]() $\mathrm {BS}(1,n)$, with
$\mathrm {BS}(1,n)$, with ![]() $n > 1$, is locally indicable, solvable, and of finite type, but it is not virtually Abelian (nor is it polycyclic-by-finite). The assumption that
$n > 1$, is locally indicable, solvable, and of finite type, but it is not virtually Abelian (nor is it polycyclic-by-finite). The assumption that ![]() $G$ be (virtually) of type
$G$ be (virtually) of type ![]() $\mathtt {FP}(\mathbb {Q})$ is also necessary; for example,
$\mathtt {FP}(\mathbb {Q})$ is also necessary; for example, ![]() $\mathbb {Z} \wr \mathbb {Z}$ is RFRS and amenable, yet it is not virtually Abelian.
$\mathbb {Z} \wr \mathbb {Z}$ is RFRS and amenable, yet it is not virtually Abelian.
Baer's conjecture states that if ![]() $G$ is a group with a Noetherian group ring
$G$ is a group with a Noetherian group ring ![]() $\mathbb {Z} G$, then
$\mathbb {Z} G$, then ![]() $G$ is a polycyclic-by-finite group. The author is grateful to Sam Hughes for pointing out the following consequence of Theorem 7.4, which resolves a special case of Baer's conjecture.
$G$ is a polycyclic-by-finite group. The author is grateful to Sam Hughes for pointing out the following consequence of Theorem 7.4, which resolves a special case of Baer's conjecture.
Corollary 7.6 Let ![]() $G$ be a virtually RFRS group of type
$G$ be a virtually RFRS group of type ![]() $\mathtt {FP}(\mathbb {Q})$. If
$\mathtt {FP}(\mathbb {Q})$. If ![]() $\mathbb {Z} G$ is Noetherian, then
$\mathbb {Z} G$ is Noetherian, then ![]() $G$ is virtually Abelian.
$G$ is virtually Abelian.
Proof. It is enough to prove the claim in the case that ![]() $G$ is RFRS. In this case,
$G$ is RFRS. In this case, ![]() $\mathbb {Z} G$ embeds into the Linnell skew-field
$\mathbb {Z} G$ embeds into the Linnell skew-field ![]() $\mathcal {D}(G)$, and therefore
$\mathcal {D}(G)$, and therefore ![]() $\mathbb {Z} G$ is a domain. Since Noetherian domains are Ore domains [Reference McConnell and RobsonMR01, p. 47], we have that
$\mathbb {Z} G$ is a domain. Since Noetherian domains are Ore domains [Reference McConnell and RobsonMR01, p. 47], we have that ![]() $\mathbb {Z} G$ is an Ore domain. It then follows that
$\mathbb {Z} G$ is an Ore domain. It then follows that ![]() $\mathbb {Q} G$ is an Ore domain, which implies that
$\mathbb {Q} G$ is an Ore domain, which implies that ![]() $G$ is amenable by Kielak's appendix to [Reference BartholdiBar19]. Then
$G$ is amenable by Kielak's appendix to [Reference BartholdiBar19]. Then ![]() $G$ is polycyclic-by-finite by Theorem 7.4.
$G$ is polycyclic-by-finite by Theorem 7.4.
7.2 Arithmetic lattices and subgroups of hyperbolic groups
Recall that hyperbolic groups are always of type ![]() $\mathtt {F}_\infty$ (and of type
$\mathtt {F}_\infty$ (and of type ![]() $\mathtt {F}$ if they are torsion-free). However, their subgroups can exhibit many interesting finiteness properties. In [Reference RipsRip82], Rips gave the first example of an incoherent hyperbolic group; phrased in terms of finiteness properties, this gives an example of a hyperbolic group with a subgroup that is of type
$\mathtt {F}$ if they are torsion-free). However, their subgroups can exhibit many interesting finiteness properties. In [Reference RipsRip82], Rips gave the first example of an incoherent hyperbolic group; phrased in terms of finiteness properties, this gives an example of a hyperbolic group with a subgroup that is of type ![]() $\mathtt {F}_1$ but not
$\mathtt {F}_1$ but not ![]() $\mathtt {F}_2$. In [Reference BradyBra99], Brady constructed a type
$\mathtt {F}_2$. In [Reference BradyBra99], Brady constructed a type ![]() $\mathtt {F}_2$ subgroup of a hyperbolic group that is not of type
$\mathtt {F}_2$ subgroup of a hyperbolic group that is not of type ![]() $\mathtt {F}_3$; this provided the first example of a finitely presented non-hyperbolic subgroup of a hyperbolic group. In the same paper, Brady asked whether there are subgroups of hyperbolic groups that are of type
$\mathtt {F}_3$; this provided the first example of a finitely presented non-hyperbolic subgroup of a hyperbolic group. In the same paper, Brady asked whether there are subgroups of hyperbolic groups that are of type ![]() $\mathtt {F}_n$ but not
$\mathtt {F}_n$ but not ![]() $\mathtt {F}_{n+1}$ for all
$\mathtt {F}_{n+1}$ for all ![]() $n$. More examples of
$n$. More examples of ![]() $\mathtt {F}_2$-not-
$\mathtt {F}_2$-not-![]() $\mathtt {F}_3$ subgroups of hyperbolic groups were provided by Kropholler [Reference KrophollerKro21] and Lodha [Reference LodhaLod18], and in [Reference Llosa Isenrich, Martelli and PyLMP21], Llosa Isenrich, Martelli and Py constructed the first examples of
$\mathtt {F}_3$ subgroups of hyperbolic groups were provided by Kropholler [Reference KrophollerKro21] and Lodha [Reference LodhaLod18], and in [Reference Llosa Isenrich, Martelli and PyLMP21], Llosa Isenrich, Martelli and Py constructed the first examples of ![]() $\mathtt {F}_3$-not-
$\mathtt {F}_3$-not-![]() $\mathtt {F}_4$ subgroups of hyperbolic groups. This result was extended in a subsequent paper [Reference Llosa Isenrich and PyLP24], where Llosa Isenrich and Py completely answer Brady's question by exhibiting cocompact hyperbolic arithmetic lattices in
$\mathtt {F}_4$ subgroups of hyperbolic groups. This result was extended in a subsequent paper [Reference Llosa Isenrich and PyLP24], where Llosa Isenrich and Py completely answer Brady's question by exhibiting cocompact hyperbolic arithmetic lattices in ![]() $\mathrm {PU}(n,1)$ with
$\mathrm {PU}(n,1)$ with ![]() $\mathtt {F}_{n-1}$-not-
$\mathtt {F}_{n-1}$-not-![]() $\mathtt {F}_n$ subgroups for all
$\mathtt {F}_n$ subgroups for all ![]() $n$. We also mention the related work of Italiano, Martelli and Migliorini, who constructed the first example of a non-hyperbolic type
$n$. We also mention the related work of Italiano, Martelli and Migliorini, who constructed the first example of a non-hyperbolic type ![]() $\mathtt {F}$ subgroup of a hyperbolic group [Reference Italiano, Martelli and MiglioriniIMM23].
$\mathtt {F}$ subgroup of a hyperbolic group [Reference Italiano, Martelli and MiglioriniIMM23].
In [Reference Llosa Isenrich, Martelli and PyLMP21], Llosa Isenrich, Martelli and Py remark that one can use Theorem 6.11 to show that there are subgroups of hyperbolic lattices in ![]() $\mathrm {PO}(2n,1)$ that are of type
$\mathrm {PO}(2n,1)$ that are of type ![]() $\mathtt {FP}_{n-1}(\mathbb {Q})$ but not
$\mathtt {FP}_{n-1}(\mathbb {Q})$ but not ![]() $\mathtt {FP}_n(\mathbb {Q})$. We record their argument here, and also mention that the same line of reasoning shows that there are many hyperbolic lattices in
$\mathtt {FP}_n(\mathbb {Q})$. We record their argument here, and also mention that the same line of reasoning shows that there are many hyperbolic lattices in ![]() $\mathrm {PO}(2n+1,1)$ that virtually fibre with kernel of type
$\mathrm {PO}(2n+1,1)$ that virtually fibre with kernel of type ![]() $\mathtt {FP}(\mathbb {Q})$.
$\mathtt {FP}(\mathbb {Q})$.
Proposition 7.7 [Reference Llosa Isenrich, Martelli and PyLMP21, Proposition 19]
Let ![]() $\Gamma < \mathrm {PO}(n,1)$ be a cocompact cubulable lattice. If
$\Gamma < \mathrm {PO}(n,1)$ be a cocompact cubulable lattice. If ![]() $n = 2k$ is even, then
$n = 2k$ is even, then ![]() $\Gamma$ virtually fibres with kernel of type
$\Gamma$ virtually fibres with kernel of type ![]() $\mathtt {FP}_{k-1}(\mathbb {Q})$ but not
$\mathtt {FP}_{k-1}(\mathbb {Q})$ but not ![]() $\mathtt {FP}_k(\mathbb {Q})$. If
$\mathtt {FP}_k(\mathbb {Q})$. If ![]() $n$ is odd, then
$n$ is odd, then ![]() $\Gamma$ virtually fibres with kernel of type
$\Gamma$ virtually fibres with kernel of type ![]() $\mathtt {FP}(\mathbb {Q})$.
$\mathtt {FP}(\mathbb {Q})$.
Remark 7.8 In [Reference Bergeron, Haglund and WiseBHW11], Bergeron, Haglund and Wise show that any standard arithmetic subgroup of ![]() $\mathrm {PO}(n,1)$ is cubulated, so Proposition 7.7 applies to a nonempty class of groups. We refer the reader to their paper for the definition of standard.
$\mathrm {PO}(n,1)$ is cubulated, so Proposition 7.7 applies to a nonempty class of groups. We refer the reader to their paper for the definition of standard.
Proof. By Agol's theorem [Reference AgolAgo13, Theorem 1.1], ![]() $\Gamma$ is virtually special and in particular virtually RFRS. By, for instance, [Reference KammeyerKam14, Theorem 3.3], the
$\Gamma$ is virtually special and in particular virtually RFRS. By, for instance, [Reference KammeyerKam14, Theorem 3.3], the ![]() $\ell ^2$-Betti numbers of lattices in semisimple Lie groups vanish except in the middle dimension, where they are nonzero. If
$\ell ^2$-Betti numbers of lattices in semisimple Lie groups vanish except in the middle dimension, where they are nonzero. If ![]() $n = 2k$, then
$n = 2k$, then ![]() $\Gamma$ virtually fibres with kernel of type
$\Gamma$ virtually fibres with kernel of type ![]() $\mathtt {FP}_{k-1}(\mathbb {Q})$, but
$\mathtt {FP}_{k-1}(\mathbb {Q})$, but ![]() $b_k^{(2)}(\Gamma ) \neq 0$ so the kernel cannot be of type
$b_k^{(2)}(\Gamma ) \neq 0$ so the kernel cannot be of type ![]() $\mathtt {FP}_n(\mathbb {Q})$ by Theorem 6.7. If
$\mathtt {FP}_n(\mathbb {Q})$ by Theorem 6.7. If ![]() $n$ is odd, then
$n$ is odd, then ![]() $\Gamma$ is
$\Gamma$ is ![]() $\ell ^2$-acyclic and, therefore, virtually fibres with kernel of type
$\ell ^2$-acyclic and, therefore, virtually fibres with kernel of type ![]() $\mathtt {FP}(\mathbb {Q})$ in this case, where we have also used Corollary 6.8.
$\mathtt {FP}(\mathbb {Q})$ in this case, where we have also used Corollary 6.8.
Acknowledgements
The author would like to thank Dawid Kielak for numerous helpful conversations and comments on this paper, Peter Kropholler for a helpful correspondence, and Sam Hughes for pointing out the application of Theorem 7.4 to Corollary 7.6. The author also thanks Sami Douba for pointing out that a polycyclic RFRS group must, in fact, be Abelian.
Conflicts of interest
None.
Financial support
This work has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (Grant agreement No. 850930).
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.