Article contents
A higher-dimensional generalization of Lichtenbaum duality in terms of the Albanese map
Published online by Cambridge University Press: 14 July 2016
Abstract
In this article, we present a conjectural formula describing the cokernel of the Albanese map of zero-cycles of smooth projective varieties 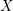 $X$ over
$X$ over 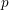 $p$ -adic fields in terms of the Néron–Severi group and provide a proof under additional assumptions on an integral model of
$p$ -adic fields in terms of the Néron–Severi group and provide a proof under additional assumptions on an integral model of 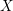 $X$ . The proof depends on a non-degeneracy result of Brauer–Manin pairing due to Saito–Sato and on Gabber–de Jong’s comparison result of cohomological and Azumaya–Brauer groups. We will also mention the local–global problem for the Albanese cokernel; the abelian group on the ‘local side’ turns out to be a finite group.
$X$ . The proof depends on a non-degeneracy result of Brauer–Manin pairing due to Saito–Sato and on Gabber–de Jong’s comparison result of cohomological and Azumaya–Brauer groups. We will also mention the local–global problem for the Albanese cokernel; the abelian group on the ‘local side’ turns out to be a finite group.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author 2016
References
- 1
- Cited by


