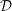Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-22T19:30:05.589Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher Chow cycles on Abelian surfaces and a non-Archimedean analogue of the Hodge-${\mathcal{D}}$-conjecture

Part of: Cycles and subschemes $K$-theory in geometry Arithmetic problems. Diophantine geometry Arithmetic algebraic geometry

Published online by Cambridge University Press:  26 March 2014

Ramesh Sreekantan
Ramesh Sreekantan*
Affiliation:
Indian Statistical Institute, Bangalore, India email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct new indecomposable elements in the higher Chow group 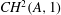$CH^2(A,1)$ of a principally polarized Abelian surface over a 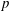$p$-adic local field, which generalize an element constructed by Collino [Griffiths’ infinitesimal invariant and higher K-theory on hyperelliptic Jacobians, J. Algebraic Geom. 6 (1997), 393–415]. These elements are constructed using a generalization, due to Birkenhake and Wilhelm [Humbert surfaces and the Kummer plane, Trans. Amer. Math. Soc. 355 (2003), 1819–1841 (electronic)], of a classical construction of Humbert. They can be used to prove a non-Archimedean analogue of the Hodge-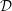${\mathcal{D}}$-conjecture – namely, the surjectivity of the boundary map in the localization sequence – in the case where the Abelian surface has good and ordinary reduction.

Keywords

higher Chow groupsrational curvesAbelian surfaces

MSC classification

Secondary: 19E15: Algebraic cycles and motivic cohomology 11G25: Varieties over finite and local fields 14C15: (Equivariant) Chow groups and rings; motives 14G20: Local ground fields
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 4 , April 2014 , pp. 691 - 711
Copyright
© The Author 2014 

References

Artin, M., Algebraic approximation of structures over complete local rings, Publ. Math. Inst. Hautes Études Sci. (1969), 23–58.CrossRefGoogle Scholar
Asakura, M. and Saito, S., Surfaces over a p-adic field with infinite torsion in the Chow group of 0-cycles, Algebra Number Theory 1 (2007), 163–181.Google Scholar
Bogomolov, F., Hassett, B. and Tschinkel, Y., Constructing rational curves on K3 surfaces, Duke Math. J. 157 (2011), 535–550.Google Scholar
Bloch, S., Algebraic cycles and higher K-theory, Adv. Math. 61 (1986), 267–304.CrossRefGoogle Scholar
Birkenhake, C. and Wilhelm, H., Humbert surfaces and the Kummer plane, Trans. Amer. Math. Soc. 355 (2003), 1819–1841; (electronic).Google Scholar
Chen, X. and Lewis, J. D., The Hodge-D-conjecture for K3 and abelian surfaces, J. Algebraic Geom. 14 (2005), 213–240.Google Scholar
Collino, A., Griffiths’ infinitesimal invariant and higher K-theory on hyperelliptic Jacobians, J. Algebraic Geom. 6 (1997), 393–415.Google Scholar
Consani, C., Double complexes and Euler L-factors, Compositio Math. 111 (1998), 323–358.Google Scholar
Elkik, R., Solution d’équations au-dessus d’anneaux henséliens, in Quelques problèmes de modules (Sém. Géom. Anal., École Norm. Sup., Paris, 1971–1972), Astérisque, vol. 16 (Soc. Math., France, Paris, 1974), 116–132.Google Scholar
Flach, M., A finiteness theorem for the symmetric square of an elliptic curve, Invent. Math. 109 (1992), 307–327.Google Scholar
Hartshorne, R., Deformation theory, Graduate Texts in Mathematics, vol. 257 (Springer, New York, 2010).Google Scholar
Jakob, B., Poncelet 5-gons and abelian surfaces, Manuscripta Math. 83 (1994), 183–198.CrossRefGoogle Scholar
Jannsen, U., Deligne homology, Hodge-D-conjecture, and motives, in Beĭlinson’s conjectures on special values of L-functions, Perspectives in Mathematics, vol. 4 (Academic Press, Boston, 1988), 305–372.Google Scholar
Lang, S., Introduction to Arakelov theory (Springer, New York, 1988).Google Scholar
Mildenhall, S. J. M., Cycles in a product of elliptic curves, and a group analogous to the class group, Duke Math. J. 67 (1992), 387–406.Google Scholar
Mori, S. and Mukai, S., The uniruledness of the moduli space of curves of genus 11, in Algebraic geometry (Tokyo/Kyoto, 1982), Lecture Notes in Mathematics, vol. 1016 (Springer, Berlin, 1983), 334–353.Google Scholar
Müller-Stach, S. J., Constructing indecomposable motivic cohomology classes on algebraic surfaces, J. Algebraic Geom. 6 (1997), 513–543.Google Scholar
Ramakrishnan, D., Regulators, algebraic cycles, and values of L-functions, in Algebraic K-theory and algebraic number theory (Honolulu, HI, 1987), Contemporary Mathematics, vol. 83 (American Mathematical Society, Providence, RI, 1989), 183–310.CrossRefGoogle Scholar
Spiess, M., On indecomposable elements of K 1of a product of elliptic curves, K-Theory 17 (1999), 363–383.Google Scholar
Sreekantan, R., Relations among Heegner cycles on families of abelian surfaces, Compositio Math. 127 (2001), 243–271.Google Scholar
Sreekantan, R., A non-Archimedean analogue of the Hodge-D-conjecture for products of elliptic curves, J. Algebraic Geom. 17 (2008), 781–798.Google Scholar
Sreekantan, R., K 1of products of Drinfeld modular curves and special values of L-functions, Compositio Math. 146 (2010), 886–918.Google Scholar
Tate, J., Endomorphisms of abelian varieties over finite fields, Invent. Math. 2 (1966), 134–144.Google Scholar