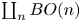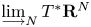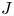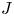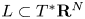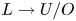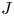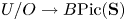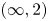1. Introduction
Let ![]() $X$ be a smooth manifold whose cotangent bundle
$X$ be a smooth manifold whose cotangent bundle ![]() $T^*X$ is equipped with the standard Liouville 1-form
$T^*X$ is equipped with the standard Liouville 1-form ![]() $\alpha =-\mathbf {p} d\mathbf {q}$. Let
$\alpha =-\mathbf {p} d\mathbf {q}$. Let ![]() $L$ be any (immersed) Lagrangian submanifold in
$L$ be any (immersed) Lagrangian submanifold in ![]() $T^*X$ exact with respect to
$T^*X$ exact with respect to ![]() $\alpha$, i.e.
$\alpha$, i.e. ![]() $-\alpha |_L$ is an exact 1-form. Let
$-\alpha |_L$ is an exact 1-form. Let ![]() $\mathbf {S}$ denote the sphere spectrum. In joint work with Treumann [Reference Jin and TreumannJT24], we use microlocal sheaf theory to construct a local system of stable
$\mathbf {S}$ denote the sphere spectrum. In joint work with Treumann [Reference Jin and TreumannJT24], we use microlocal sheaf theory to construct a local system of stable ![]() $\infty$-categories on
$\infty$-categories on ![]() $L$ with fiber equivalent to the
$L$ with fiber equivalent to the ![]() $\infty$-category of spectra, which we call the sheaf of brane structures and denote by
$\infty$-category of spectra, which we call the sheaf of brane structures and denote by ![]() $\mathrm {Brane}_L$. The sheaf of brane structures admits a classifying map
$\mathrm {Brane}_L$. The sheaf of brane structures admits a classifying map ![]() $L\rightarrow B\mathrm {Pic}(\mathbf {S})$, where the target is the delooping of the
$L\rightarrow B\mathrm {Pic}(\mathbf {S})$, where the target is the delooping of the ![]() $E_\infty$-groupoid of (suspensions of)
$E_\infty$-groupoid of (suspensions of) ![]() $\mathbf {S}$-lines. In [Reference Jin and TreumannJT24], we make the following claim (without proof).
$\mathbf {S}$-lines. In [Reference Jin and TreumannJT24], we make the following claim (without proof).
Claim 1.1 The classifying map of ![]() $\mathrm {Brane}_L$ factors as
$\mathrm {Brane}_L$ factors as
in which ![]() $\gamma$ is the stable Gauss mapFootnote 1 into the stable Lagrangian Grassmannian
$\gamma$ is the stable Gauss mapFootnote 1 into the stable Lagrangian Grassmannian ![]() $U/O$ and
$U/O$ and ![]() $BJ$ is the delooping of the
$BJ$ is the delooping of the ![]() $J$-homomorphism
$J$-homomorphism
as an ![]() $E_\infty$-map.
$E_\infty$-map.
The goal of this paper is three-fold. First, it will combine with [Reference JinJin20] to give a proof of the claim. Second, it enhances the main theorem of stratified Morse theory with the rich structures of the ![]() $J$-homomorphism. Last but not least, this work employs the category of correspondences developed in [Reference Gaitsgory and RozenblyumGR17], and we have produced several concrete constructions of (commutative) algebra/module objects and (right-lax) morphisms between them in the symmetric monoidal
$J$-homomorphism. Last but not least, this work employs the category of correspondences developed in [Reference Gaitsgory and RozenblyumGR17], and we have produced several concrete constructions of (commutative) algebra/module objects and (right-lax) morphisms between them in the symmetric monoidal ![]() $(\infty,2)$-category of correspondences, which we hope could lead to more applications.
$(\infty,2)$-category of correspondences, which we hope could lead to more applications.
In the following, we summarize the key ingredients and main results. We also sketch the remaining steps in [Reference JinJin20] to complete the proof of the above claim.
1.1 A Hamiltonian  $\coprod _n BO(n)$-action and Bott periodicity
$\coprod _n BO(n)$-action and Bott periodicity
In ![]() $T^*\mathbf {R}^N$, for any quadratic form
$T^*\mathbf {R}^N$, for any quadratic form ![]() $A$ on
$A$ on ![]() $\mathbf {R}^N$, we consider the quadratic Hamiltonian function
$\mathbf {R}^N$, we consider the quadratic Hamiltonian function ![]() $F_A(\mathbf {q},\mathbf {p})=A(\mathbf {p})$. Here we identify
$F_A(\mathbf {q},\mathbf {p})=A(\mathbf {p})$. Here we identify ![]() $(\mathbf {R}^N)^*$ with
$(\mathbf {R}^N)^*$ with ![]() $\mathbf {R}^N$ using the standard inner product on
$\mathbf {R}^N$ using the standard inner product on ![]() $\mathbf {R}^N$. The time-1 flow
$\mathbf {R}^N$. The time-1 flow ![]() $\varphi _A^1$ of the Hamiltonian vector field
$\varphi _A^1$ of the Hamiltonian vector field ![]() $X_{F_A}$ of
$X_{F_A}$ of ![]() $F_A$, defined as
$F_A$, defined as ![]() $\omega (X_{F_A},-)=dF_A$, sends
$\omega (X_{F_A},-)=dF_A$, sends ![]() $(\mathbf {q},\mathbf {p})$ to
$(\mathbf {q},\mathbf {p})$ to ![]() $(\mathbf {q}+\partial _{\mathbf {p}}A(\mathbf {p}), \mathbf {p})$. In the following, we assume that
$(\mathbf {q}+\partial _{\mathbf {p}}A(\mathbf {p}), \mathbf {p})$. In the following, we assume that ![]() $A$ as a symmetric matrix is idempotent, i.e. there exists a subspace
$A$ as a symmetric matrix is idempotent, i.e. there exists a subspace ![]() $E_A\subset \mathbf {R}^N$ such that
$E_A\subset \mathbf {R}^N$ such that ![]() $A(\mathbf {p})=|\mathrm {proj}_{E_A}\mathbf {p}|^2$. If we start with the linear Lagrangian
$A(\mathbf {p})=|\mathrm {proj}_{E_A}\mathbf {p}|^2$. If we start with the linear Lagrangian ![]() $L_0$ that is the graph of the differential of
$L_0$ that is the graph of the differential of ![]() $-\frac {1}{2}|\mathbf {q}|^2$, and do
$-\frac {1}{2}|\mathbf {q}|^2$, and do ![]() $\varphi _A^1$ to it, then the resulting Lagrangian
$\varphi _A^1$ to it, then the resulting Lagrangian ![]() $L_A$ is the graph of the differential of
$L_A$ is the graph of the differential of ![]() $-\frac {1}{2}|\mathbf {q}|^2+A(\mathbf {q})$. Moreover, the Maslov index of the loop starting from
$-\frac {1}{2}|\mathbf {q}|^2+A(\mathbf {q})$. Moreover, the Maslov index of the loop starting from ![]() $L_0$, going towards
$L_0$, going towards ![]() $L_A$ via the Hamiltonian flow of
$L_A$ via the Hamiltonian flow of ![]() $F_A$ and finally going back to
$F_A$ and finally going back to ![]() $L_0$ through the path by decreasing the eigenvalue of
$L_0$ through the path by decreasing the eigenvalue of ![]() $A$ from
$A$ from ![]() $1$ to
$1$ to ![]() $0$ is exactly the rank of
$0$ is exactly the rank of ![]() $A$ (up to a negative sign). We can conjugate this loop by the path connecting the zero-section to
$A$ (up to a negative sign). We can conjugate this loop by the path connecting the zero-section to ![]() $L_0$ through the graphs of differentials of
$L_0$ through the graphs of differentials of ![]() $-\frac {1}{2}t|\mathbf {q}|^2, t\in [0,1]$ so then the base point is always at the zero-section.
$-\frac {1}{2}t|\mathbf {q}|^2, t\in [0,1]$ so then the base point is always at the zero-section.
If we take the stabilization ![]() $\varinjlim _NT^*\mathbf {R}^N$, then the above picture tells us a way to assign a based loop in the stable Lagrangian Grassmannian
$\varinjlim _NT^*\mathbf {R}^N$, then the above picture tells us a way to assign a based loop in the stable Lagrangian Grassmannian ![]() $U/O$ from an element in
$U/O$ from an element in ![]() $\coprod _{n}Gr(n,\mathbf {R}^\infty )=\coprod _{n}BO(n)$, which is exactly the content of (a part of) Bott periodicity that the latter after taking group completion is the based loop space of the former. Now it is natural to assemble the Hamiltonian map for different choices of
$\coprod _{n}Gr(n,\mathbf {R}^\infty )=\coprod _{n}BO(n)$, which is exactly the content of (a part of) Bott periodicity that the latter after taking group completion is the based loop space of the former. Now it is natural to assemble the Hamiltonian map for different choices of ![]() $A$ as a Hamiltonian
$A$ as a Hamiltonian ![]() $\coprod _{n}BO(n)$-action on
$\coprod _{n}BO(n)$-action on ![]() $\varinjlim _NT^*\mathbf {R}^N$. Here we take the standard commutative topological monoid structure on
$\varinjlim _NT^*\mathbf {R}^N$. Here we take the standard commutative topological monoid structure on ![]() $\coprod _{n}BO(n)$ as in [Reference HarrisHar80], where the addition operation is only defined for two perpendicular finite dimensional subspaces in
$\coprod _{n}BO(n)$ as in [Reference HarrisHar80], where the addition operation is only defined for two perpendicular finite dimensional subspaces in ![]() $\varinjlim _N\mathbf {R}^N$.
$\varinjlim _N\mathbf {R}^N$.
1.2 Quantization of the Hamiltonian  $\coprod _n BO(n)$-action and a natural “module”
$\coprod _n BO(n)$-action and a natural “module”
We use microlocal sheaf theory to study the Hamiltonian ![]() $\coprod _n BO(n)$-action described above. The standard way to do this is to find a sheaf over prescribed coefficient with singular support in a conic Lagrangian lifting of the moment Lagrangian of the Hamiltonian action, called sheaf quantization (cf. [Reference Guillermou, Kashiwara and SchapiraGKS12, Reference TamarkinTam15]). Here we take the coefficient to be the universal one, the sphere spectrum
$\coprod _n BO(n)$-action described above. The standard way to do this is to find a sheaf over prescribed coefficient with singular support in a conic Lagrangian lifting of the moment Lagrangian of the Hamiltonian action, called sheaf quantization (cf. [Reference Guillermou, Kashiwara and SchapiraGKS12, Reference TamarkinTam15]). Here we take the coefficient to be the universal one, the sphere spectrum ![]() $\mathbf {S}$, so sheaves are taking values in the stable
$\mathbf {S}$, so sheaves are taking values in the stable ![]() $\infty$-category of spectra
$\infty$-category of spectra ![]() $\mathrm {Sp}$ (see [Reference Jin and TreumannJT24] for basic properties of microlocal sheaves of spectra). The commutative monoid structure on
$\mathrm {Sp}$ (see [Reference Jin and TreumannJT24] for basic properties of microlocal sheaves of spectra). The commutative monoid structure on ![]() $\coprod _n BO(n)$ endows the associated sheaf category with a symmetric monoidal convolution structure (we will make this precise by using the category of correspondence developed in [Reference Gaitsgory and RozenblyumGR17]), and it is natural to ask the sought-for sheaf to be a commutative algebra object in it. Moreover, to establish a connection of the Hamiltonian action with Maslov index and Bott periodicity, etc., we need to quantize a ‘module’ of it generated by (the stabilization of)
$\coprod _n BO(n)$ endows the associated sheaf category with a symmetric monoidal convolution structure (we will make this precise by using the category of correspondence developed in [Reference Gaitsgory and RozenblyumGR17]), and it is natural to ask the sought-for sheaf to be a commutative algebra object in it. Moreover, to establish a connection of the Hamiltonian action with Maslov index and Bott periodicity, etc., we need to quantize a ‘module’ of it generated by (the stabilization of) ![]() $L_0$ as well. We will make this more precise below.
$L_0$ as well. We will make this more precise below.
For any smooth manifold ![]() $X$, let
$X$, let ![]() $T^{*,<0}(X\times \mathbf {R}_t)$ be the negative half of
$T^{*,<0}(X\times \mathbf {R}_t)$ be the negative half of ![]() $T^*(X\times \mathbf {R}_t)$, where every covector has strictly negative component in
$T^*(X\times \mathbf {R}_t)$, where every covector has strictly negative component in ![]() ${\rm d}t$. For any exact Lagrangian submanifold
${\rm d}t$. For any exact Lagrangian submanifold ![]() $L$ in
$L$ in ![]() $T^*X$, a conic lifting
$T^*X$, a conic lifting ![]() $\mathbf {L}$ of
$\mathbf {L}$ of ![]() $L$ in
$L$ in ![]() $T^{*,<0}(X\times \mathbf {R}_t)$ (with the Liouville 1-form
$T^{*,<0}(X\times \mathbf {R}_t)$ (with the Liouville 1-form ![]() $-\tau \, {\rm d}t+\alpha$) is any conic Lagrangian, i.e. invariant under the
$-\tau \, {\rm d}t+\alpha$) is any conic Lagrangian, i.e. invariant under the ![]() $\mathbf {R}_+$-scaling on the fibers, determined by the properties that:
$\mathbf {R}_+$-scaling on the fibers, determined by the properties that:
– the projection to
 $T^*X$ sends
$T^*X$ sends  $\mathbf {L}\cap \{\tau =-1\}$ isomorphicallyFootnote 2 to
$\mathbf {L}\cap \{\tau =-1\}$ isomorphicallyFootnote 2 to  $L$.
$L$.
By the conic property, the 1-form ![]() $-\tau \, {\rm d}t+\alpha$ vanishes on
$-\tau \, {\rm d}t+\alpha$ vanishes on ![]() $\mathbf {L}$, which is equivalent to saying that
$\mathbf {L}$, which is equivalent to saying that ![]() $\mathbf {L}\cap \{\tau =-1\}$ is a Legendrian submanifold in the contact hypersurface
$\mathbf {L}\cap \{\tau =-1\}$ is a Legendrian submanifold in the contact hypersurface ![]() $(\{\tau =-1\}\cong T^*X\times \mathbf {R}_t, {\rm d}t+\alpha )$ that projects to
$(\{\tau =-1\}\cong T^*X\times \mathbf {R}_t, {\rm d}t+\alpha )$ that projects to ![]() $L$ isomorphically. The latter is usually referred to as a Legendrian lifting of
$L$ isomorphically. The latter is usually referred to as a Legendrian lifting of ![]() $L$. In other words, by writing
$L$. In other words, by writing ![]() $-\alpha |_{L}=df$, its Legendrian lifting (for the choice of
$-\alpha |_{L}=df$, its Legendrian lifting (for the choice of ![]() $f$) is just the graph of
$f$) is just the graph of ![]() $t=f(\mathbf {q}, \mathbf {p})$ with
$t=f(\mathbf {q}, \mathbf {p})$ with ![]() $(\mathbf {q}, \mathbf {p})\in L$, and
$(\mathbf {q}, \mathbf {p})\in L$, and ![]() $\mathbf {L}$ is its conification. For more details about Legendrian liftings and their conification, we refer the reader to [Reference Jin and TreumannJT24, § 3.1–3.5] (note that in [Reference Jin and TreumannJT24] there is some sign difference: we used
$\mathbf {L}$ is its conification. For more details about Legendrian liftings and their conification, we refer the reader to [Reference Jin and TreumannJT24, § 3.1–3.5] (note that in [Reference Jin and TreumannJT24] there is some sign difference: we used ![]() $\alpha =\mathbf {p} d\mathbf {q}$ instead of
$\alpha =\mathbf {p} d\mathbf {q}$ instead of ![]() $-\mathbf {p} d\mathbf {q}$). For any exact Lagrangian in general position,
$-\mathbf {p} d\mathbf {q}$). For any exact Lagrangian in general position, ![]() $\mathbf {L}$ is completely determined by the front projection of
$\mathbf {L}$ is completely determined by the front projection of ![]() $\mathbf {L}$ in
$\mathbf {L}$ in ![]() $X\times \mathbf {R}_t$, i.e. its image under the projection
$X\times \mathbf {R}_t$, i.e. its image under the projection ![]() $T^{*,<0}(X\times \mathbf {R}_t)\rightarrow X\times \mathbf {R}_t$ to the base. Moreover, if
$T^{*,<0}(X\times \mathbf {R}_t)\rightarrow X\times \mathbf {R}_t$ to the base. Moreover, if ![]() $L$ is closed and the front projection of
$L$ is closed and the front projection of ![]() $\mathbf {L}$ is a smooth submanifold, then
$\mathbf {L}$ is a smooth submanifold, then ![]() $\mathbf {L}$ is just half of the conormal bundle of the submanifold with negative
$\mathbf {L}$ is just half of the conormal bundle of the submanifold with negative ![]() $dt$-component, and we say it is the negative conormal bundle of the smooth submanifold.
$dt$-component, and we say it is the negative conormal bundle of the smooth submanifold.
A (stabilized) conic Lagrangian lifting of the graph of the Hamiltonian action has front projection in ![]() $\coprod _n BO(n)\times \varinjlim _M\mathbf {R}^M\times \varinjlim _M\mathbf {R}^M\times \mathbf {R}_t$ consisting of points
$\coprod _n BO(n)\times \varinjlim _M\mathbf {R}^M\times \varinjlim _M\mathbf {R}^M\times \mathbf {R}_t$ consisting of points
which is a smooth subvariety. Here and after, by some abuse of notation, we will use ![]() $A$ to denote its eigenspace
$A$ to denote its eigenspace ![]() $E_A$ of
$E_A$ of ![]() $1$ as well, so then
$1$ as well, so then ![]() $A$ also represents an element in
$A$ also represents an element in ![]() $\coprod _n BO(n)$.
$\coprod _n BO(n)$.
Note that we can equally represent a point in (1.2.1) by
Then modulo the roles of ![]() $\mathbf {q}$ and
$\mathbf {q}$ and ![]() $t$, which contribute trivially to the topology, the front projection is just the tautological vector bundle on
$t$, which contribute trivially to the topology, the front projection is just the tautological vector bundle on ![]() $\coprod _n BO(n)$.
$\coprod _n BO(n)$.
Let
 \begin{gather} G_N=\coprod_n
Gr(n,\mathbf{R}^N),\quad VG_N=\text{the tautological vector
bundle on } G_N,\nonumber\\ G=\varinjlim_{N}G_N=\coprod_n
BO(n),\quad VG=\varinjlim_{N}VG_N.
\end{gather}
\begin{gather} G_N=\coprod_n
Gr(n,\mathbf{R}^N),\quad VG_N=\text{the tautological vector
bundle on } G_N,\nonumber\\ G=\varinjlim_{N}G_N=\coprod_n
BO(n),\quad VG=\varinjlim_{N}VG_N.
\end{gather}
A quantization of the Hamiltonian ![]() $G$-action is then given by a commutative algebra object in
$G$-action is then given by a commutative algebra object in
equipped with the convolution symmetric monoidal structure, whose restriction to the unit ![]() ${(A=0, \mathbf {p}=0)}$ of
${(A=0, \mathbf {p}=0)}$ of ![]() $VG$ is the constant sheaf
$VG$ is the constant sheaf ![]() $\mathbf {S}$ on a point. Here and after
$\mathbf {S}$ on a point. Here and after ![]() $\mathrm {Loc}(X;\mathrm {Sp})$ consists of locally constant cosheaves, and the limit of above is taken for the
$\mathrm {Loc}(X;\mathrm {Sp})$ consists of locally constant cosheaves, and the limit of above is taken for the ![]() $!$-pullback along the natural embeddings
$!$-pullback along the natural embeddings ![]() $VG_{N}\hookrightarrow VG_{N'}$ for
$VG_{N}\hookrightarrow VG_{N'}$ for ![]() $N\leq N'$ (cf. Remark 1.7 below). A canonical candidate of such a quantization is the dualizing sheaf
$N\leq N'$ (cf. Remark 1.7 below). A canonical candidate of such a quantization is the dualizing sheaf ![]() $\varpi _{VG}$.
$\varpi _{VG}$.
Now what do we mean by to quantize a ‘module’ of the Hamiltonian action generated by the stabilization of ![]() $L_0$? First, we can quantize
$L_0$? First, we can quantize ![]() $L_0\subset T^*\mathbf {R}^M$ by the
$L_0\subset T^*\mathbf {R}^M$ by the ![]() $*$-extension of a local system on
$*$-extension of a local system on
to ![]() $\mathbf {R}^M_\mathbf {q}\times \mathbf {R}_s$, whose boundary has negative conormal bundle equal to a conic lifting of
$\mathbf {R}^M_\mathbf {q}\times \mathbf {R}_s$, whose boundary has negative conormal bundle equal to a conic lifting of ![]() $L_0$. Second, we can assemble the images of (the stabilization of)
$L_0$. Second, we can assemble the images of (the stabilization of) ![]() $L_0$ under the Hamiltonian
$L_0$ under the Hamiltonian ![]() $G$-action, i.e.
$G$-action, i.e. ![]() $L_A=\varphi _A^1(L_0)$, into a single Lagrangian
$L_A=\varphi _A^1(L_0)$, into a single Lagrangian ![]() $\widehat {L}$ in the stable sense, and we can present a conic lifting of it as the stabilization of the negative conormal bundle of the boundary of the following domain
$\widehat {L}$ in the stable sense, and we can present a conic lifting of it as the stabilization of the negative conormal bundle of the boundary of the following domain
for ![]() $M\geq N$.
$M\geq N$.
Now the point is that given any quantization of ![]() $L_0$, represented by an object in
$L_0$, represented by an object in ![]() $\mathrm {Loc}(Q^0;\mathrm {Sp}):= \varprojlim _M \mathrm {Loc}(Q_M^0;\mathrm {Sp})$, and the canonical quantization of the Hamiltonian
$\mathrm {Loc}(Q^0;\mathrm {Sp}):= \varprojlim _M \mathrm {Loc}(Q_M^0;\mathrm {Sp})$, and the canonical quantization of the Hamiltonian ![]() $G$-action
$G$-action ![]() $\varpi _{VG}$, we should automatically get a quantization of
$\varpi _{VG}$, we should automatically get a quantization of ![]() $\widehat {L}$, which is represented by an object in
$\widehat {L}$, which is represented by an object in
This can be made precise using correspondences for sheaves. If we view ![]() $\widehat {L}$ as a ‘module’ of the Hamiltonian action generated by the stabilization of
$\widehat {L}$ as a ‘module’ of the Hamiltonian action generated by the stabilization of ![]() $L_0$, then the resulting quantizations of
$L_0$, then the resulting quantizations of ![]() $\widehat {L}$ as above are those that we are interested in. A main question that we will answer is a characterization of these quantizations of
$\widehat {L}$ as above are those that we are interested in. A main question that we will answer is a characterization of these quantizations of ![]() $\widehat {L}$, for example, what are the monodromies of the corresponding local systems on
$\widehat {L}$, for example, what are the monodromies of the corresponding local systems on ![]() $\widehat {Q}$.
$\widehat {Q}$.
1.3 Stratified Morse theory
Let ![]() $X$ be a smooth manifold and
$X$ be a smooth manifold and ![]() $\mathfrak {S}=\{S_\alpha \}$ be a Whitney stratification of
$\mathfrak {S}=\{S_\alpha \}$ be a Whitney stratification of ![]() $X$. Let
$X$. Let
be the union of the conormal bundles of the strata, which is a closed conic Lagrangian in ![]() $T^*X$. Now given any
$T^*X$. Now given any ![]() $\mathfrak {S}$-constructible sheaf
$\mathfrak {S}$-constructible sheaf ![]() $\mathcal {F}$ and a covector
$\mathcal {F}$ and a covector ![]() $(x,p)$ in the smooth locus of
$(x,p)$ in the smooth locus of ![]() $\Lambda _\mathfrak {S}$, denoted by
$\Lambda _\mathfrak {S}$, denoted by ![]() $\Lambda _\mathfrak {S}^{\rm sm}$, one can define the local Morse group or microlocal stalk of
$\Lambda _\mathfrak {S}^{\rm sm}$, one can define the local Morse group or microlocal stalk of ![]() $\mathcal {F}$ at
$\mathcal {F}$ at ![]() $(x,p)$. The definition depends on a choice of a local function
$(x,p)$. The definition depends on a choice of a local function ![]() $f$ near
$f$ near ![]() $x$ whose differential at
$x$ whose differential at ![]() $x$ is
$x$ is ![]() $p$, and which is a Morse function restricted to the stratum containing
$p$, and which is a Morse function restricted to the stratum containing ![]() $x$. Such a function is called a local stratified Morse function. Roughly speaking, the microlocal stalk measures how the local sections of
$x$. Such a function is called a local stratified Morse function. Roughly speaking, the microlocal stalk measures how the local sections of ![]() $\mathcal {F}$ change when we move across
$\mathcal {F}$ change when we move across ![]() $x$ in the way directed by
$x$ in the way directed by ![]() $f$. One uses the microlocal stalks to define the singular support of
$f$. One uses the microlocal stalks to define the singular support of ![]() $\mathcal {F}$, denoted by
$\mathcal {F}$, denoted by ![]() $\mathit {SS}(\mathcal {F})$, which is a closed conic Lagrangian contained in
$\mathit {SS}(\mathcal {F})$, which is a closed conic Lagrangian contained in ![]() $\Lambda _\mathfrak {S}$. The microlocal stalks and singular support play an essential role in microlocal sheaf theory and the theory of perverse sheaves. For example, a central question in microlocal sheaf theory is to calculate the microlocal sheaf category associated to a conic Lagrangian (or equivalently a Legendrian), which is roughly speaking a localization of the category of sheaves whose singular support are contained in the conic Lagrangian.
$\Lambda _\mathfrak {S}$. The microlocal stalks and singular support play an essential role in microlocal sheaf theory and the theory of perverse sheaves. For example, a central question in microlocal sheaf theory is to calculate the microlocal sheaf category associated to a conic Lagrangian (or equivalently a Legendrian), which is roughly speaking a localization of the category of sheaves whose singular support are contained in the conic Lagrangian.
The main theorem in stratified Morse theory [Reference Goresky and MacPhersonGM88] states (in part) that the microlocal stalk defined above is independent of the choice of the local stratified Morse functions ![]() $f$, in the sense that the microlocal stalks at
$f$, in the sense that the microlocal stalks at ![]() $(x,p)$ for two different
$(x,p)$ for two different ![]() $f_1, f_2$ are isomorphic up to a shift of degree by the difference of their Morse indices along the stratum containing
$f_1, f_2$ are isomorphic up to a shift of degree by the difference of their Morse indices along the stratum containing ![]() $x$.
$x$.
We will enhance the main theorem in stratified Morse theory by exhibiting the (stabilized) monodromies of the microlocal stalks along the space of all choices of local stratified Morse functions ![]() $f$ (cf. Theorem 1.4 below). This is an application of the quantization of the Hamiltonian
$f$ (cf. Theorem 1.4 below). This is an application of the quantization of the Hamiltonian ![]() $G$-action and its ‘module’ described above.
$G$-action and its ‘module’ described above.
1.4 The  $J$-homomorphism
$J$-homomorphism
The ![]() $J$-homomorphism is an
$J$-homomorphism is an ![]() $E_\infty$-map
$E_\infty$-map
where ![]() $\mathrm {Pic}(\mathbf {S})$ is the classifying space of stable sphere bundles. If one takes the group completion of
$\mathrm {Pic}(\mathbf {S})$ is the classifying space of stable sphere bundles. If one takes the group completion of ![]() $\coprod _{n}BO(n)$,
$\coprod _{n}BO(n)$, ![]() $\mathbf {Z}\times BO$, then one can uniquely extend
$\mathbf {Z}\times BO$, then one can uniquely extend ![]() $J$ (up to a contractible space of choices) to an
$J$ (up to a contractible space of choices) to an ![]() $\Omega ^\infty$-map from
$\Omega ^\infty$-map from ![]() $\mathbf {Z}\times BO$ to
$\mathbf {Z}\times BO$ to ![]() $\mathrm {Pic}(\mathbf {S})$. By the Thom construction, every vector bundle gives rise to a stable sphere bundle, and
$\mathrm {Pic}(\mathbf {S})$. By the Thom construction, every vector bundle gives rise to a stable sphere bundle, and ![]() $J$ is the map between the classifying space of stable vector bundles to the classifying space of stable sphere bundles.
$J$ is the map between the classifying space of stable vector bundles to the classifying space of stable sphere bundles.
There are several equivalent models of ![]() $J$ to express its
$J$ to express its ![]() $E_\infty$-structure. A model of
$E_\infty$-structure. A model of ![]() $J$ as an infinite loop space map from
$J$ as an infinite loop space map from ![]() $G$ to
$G$ to ![]() $\mathrm {Pic}(\mathbf {S})$ is given as follows (cf. [Reference LurieLur15] for the complex
$\mathrm {Pic}(\mathbf {S})$ is given as follows (cf. [Reference LurieLur15] for the complex ![]() $J$-homomorphism). Let
$J$-homomorphism). Let ![]() $\mathrm {Vect}_{\mathbf {R}}^{\simeq }$ be the topologically enriched category of real finite-dimensional vector spaces, with morphisms being linear isomorphisms. The direct sum of vector spaces makes
$\mathrm {Vect}_{\mathbf {R}}^{\simeq }$ be the topologically enriched category of real finite-dimensional vector spaces, with morphisms being linear isomorphisms. The direct sum of vector spaces makes ![]() $N(\mathrm {Vect}_{\mathbf {R}}^{\simeq })$ into a symmetric monoidal
$N(\mathrm {Vect}_{\mathbf {R}}^{\simeq })$ into a symmetric monoidal ![]() $\infty$-groupoid. For any
$\infty$-groupoid. For any ![]() $V\in \mathrm {Vect}_{\mathbf {R}}^{\simeq }$, let
$V\in \mathrm {Vect}_{\mathbf {R}}^{\simeq }$, let ![]() $V^c$ be the one-point compactification of
$V^c$ be the one-point compactification of ![]() $V$ (with the marked point at
$V$ (with the marked point at ![]() $\infty$). The functor
$\infty$). The functor ![]() $V\mapsto \Sigma ^\infty V^c$ of forming
$V\mapsto \Sigma ^\infty V^c$ of forming ![]() $\mathbf {S}$-lines determines the symmetric monoidal functor
$\mathbf {S}$-lines determines the symmetric monoidal functor
Here we give an equivalent model of ![]() $J$ using correspondences for sheaves. Let
$J$ using correspondences for sheaves. Let
be the vector bundle projection, where ![]() $G_N, VG_N$ are defined in (1.2.2). Since
$G_N, VG_N$ are defined in (1.2.2). Since ![]() $G$ and
$G$ and ![]() $VG$ are commutative topological monoids, their local system categories
$VG$ are commutative topological monoids, their local system categories ![]() $\mathrm {Loc}(G;\mathrm {Sp})$ and
$\mathrm {Loc}(G;\mathrm {Sp})$ and ![]() $\mathrm {Loc}(VG;\mathrm {Sp})$ are equipped with the convolution symmetric monoidal structures from the symmetric monoidal functor
$\mathrm {Loc}(VG;\mathrm {Sp})$ are equipped with the convolution symmetric monoidal structures from the symmetric monoidal functor
 \begin{align*} \mathrm{Fun}(-, \mathrm{Sp}): \mathcal{S}\mathrm{pc}^{\rm op}&\to \mathcal{P}\mathrm{r}_{\mathrm{st}}^{\mathrm{L}}\\ X&\mapsto \mathrm{Fun}(X,\mathrm{Sp})\simeq \mathrm{Loc}(X,\mathrm{Sp}). \end{align*}
\begin{align*} \mathrm{Fun}(-, \mathrm{Sp}): \mathcal{S}\mathrm{pc}^{\rm op}&\to \mathcal{P}\mathrm{r}_{\mathrm{st}}^{\mathrm{L}}\\ X&\mapsto \mathrm{Fun}(X,\mathrm{Sp})\simeq \mathrm{Loc}(X,\mathrm{Sp}). \end{align*}
This will agree with the symmetric monoidal structure defined in § 1.8 using correspondences in the 1-category of locally compact Hausdorff spaces and then taking inverse limits (1.2.3). Then ![]() $J$ can be viewed as a commutative algebra object in
$J$ can be viewed as a commutative algebra object in ![]() $\mathrm {Loc}(G;\mathrm {Sp})$ whose costalks are isomorphic to suspensions of the sphere spectrum. We have the following result proved in § A.4.
$\mathrm {Loc}(G;\mathrm {Sp})$ whose costalks are isomorphic to suspensions of the sphere spectrum. We have the following result proved in § A.4.
Proposition 1.2 (See Proposition 4.13)
The functor
is symmetric monoidal, and the local system ![]() $(\pi _{VG})_*\varpi _{VG}$ is the commutative algebra object in
$(\pi _{VG})_*\varpi _{VG}$ is the commutative algebra object in ![]() $\mathrm {Loc}(G;\mathrm {Sp})$ classified by
$\mathrm {Loc}(G;\mathrm {Sp})$ classified by ![]() $J$.
$J$.
Here by the dualizing sheaf on a locally compact Hausdorff space ![]() $X$, we mean the constant cosheaf with cofiber
$X$, we mean the constant cosheaf with cofiber ![]() $\mathbf {S}$, through Lurie's Verdier duality for sheaves of spectra (cf. [Reference LurieLur17, Theorem 5.5.5.1])
$\mathbf {S}$, through Lurie's Verdier duality for sheaves of spectra (cf. [Reference LurieLur17, Theorem 5.5.5.1])
Then ![]() $\varpi _{VG}$ is the object corresponding to
$\varpi _{VG}$ is the object corresponding to ![]() $\varpi _{VG_N}, N\geq 0$, under the inverse limit. We emphasize that the functor
$\varpi _{VG_N}, N\geq 0$, under the inverse limit. We emphasize that the functor ![]() $(\pi _{VG})_*$ is not well defined if we regard
$(\pi _{VG})_*$ is not well defined if we regard ![]() $\pi _{VG}$ as a morphism in the
$\pi _{VG}$ as a morphism in the ![]() $\infty$-category of spaces
$\infty$-category of spaces ![]() $\mathcal {S}\mathrm {pc}$, for it is not invariant under homotopies (note that
$\mathcal {S}\mathrm {pc}$, for it is not invariant under homotopies (note that ![]() $(\pi _{VG})_!$ is well defined but gives trivial information). This is a place where we need to work in the ordinary 1-category of locally compact Hausdorff spaces, and the validity of
$(\pi _{VG})_!$ is well defined but gives trivial information). This is a place where we need to work in the ordinary 1-category of locally compact Hausdorff spaces, and the validity of ![]() $(\pi _{VG})_*$ (which follows from base change) and its symmetric monoidal structure leads us to employ the category of correspondences.
$(\pi _{VG})_*$ (which follows from base change) and its symmetric monoidal structure leads us to employ the category of correspondences.
1.5 Statement of the main results
Now we are ready to state our main results. The space ![]() $\widehat {Q}=\varinjlim _{N,M}\widehat {Q}_{N,M}$ (see (1.2.4) for the definition of
$\widehat {Q}=\varinjlim _{N,M}\widehat {Q}_{N,M}$ (see (1.2.4) for the definition of ![]() $\widehat {Q}_{N,M}$) is naturally homotopy equivalent to
$\widehat {Q}_{N,M}$) is naturally homotopy equivalent to ![]() $G$, so we can view
$G$, so we can view ![]() $\widehat {Q}$ as a
$\widehat {Q}$ as a ![]() $G$-torsor in
$G$-torsor in ![]() $\mathcal {S}\mathrm {pc}$ (i.e. a free
$\mathcal {S}\mathrm {pc}$ (i.e. a free ![]() $G$-module generated by a point), and
$G$-module generated by a point), and ![]() $\mathrm {Loc}(\widehat {Q};\mathrm {Sp})\simeq \mathrm {Loc}(G;\mathrm {Sp})$ is naturally a module of
$\mathrm {Loc}(\widehat {Q};\mathrm {Sp})\simeq \mathrm {Loc}(G;\mathrm {Sp})$ is naturally a module of ![]() $\mathrm {Loc}(G;\mathrm {Sp})$. Let
$\mathrm {Loc}(G;\mathrm {Sp})$. Let ![]() $\mathrm {Loc}(\widehat {Q};\mathrm {Sp})^J$ be the stable
$\mathrm {Loc}(\widehat {Q};\mathrm {Sp})^J$ be the stable ![]() $\infty$-category of
$\infty$-category of ![]() $J$-equivariant local systems on
$J$-equivariant local systems on ![]() $\widehat {Q}$, which is a full subcategory of
$\widehat {Q}$, which is a full subcategory of ![]() $J$-modules in
$J$-modules in ![]() $\mathrm {Loc}(\widehat {Q};\mathrm {Sp})$. Here we use
$\mathrm {Loc}(\widehat {Q};\mathrm {Sp})$. Here we use ![]() $J$ to represent the local system on
$J$ to represent the local system on ![]() $G\simeq \widehat {Q}$ that it classifies. Since
$G\simeq \widehat {Q}$ that it classifies. Since ![]() $\widehat {Q}$ is a
$\widehat {Q}$ is a ![]() $G$-torsor,
$G$-torsor, ![]() $\mathrm {Loc}(\widehat {Q};\mathrm {Sp})^J$ consists of objects
$\mathrm {Loc}(\widehat {Q};\mathrm {Sp})^J$ consists of objects ![]() $J\otimes _{\mathbf {S}}\mathcal {R}$,
$J\otimes _{\mathbf {S}}\mathcal {R}$, ![]() $\mathcal {R}\in \mathrm {Sp}$, and the mapping spectrum from
$\mathcal {R}\in \mathrm {Sp}$, and the mapping spectrum from ![]() $J\otimes _{\mathbf {S}}\mathcal {R}_1$ to
$J\otimes _{\mathbf {S}}\mathcal {R}_1$ to ![]() $J\otimes _{\mathbf {S}}\mathcal {R}_2$ is isomorphic to the mapping spectrum from
$J\otimes _{\mathbf {S}}\mathcal {R}_2$ is isomorphic to the mapping spectrum from ![]() $\mathcal {R}_1$ to
$\mathcal {R}_1$ to ![]() $\mathcal {R}_2$ (see Lemma 4.15). There is a general definition of
$\mathcal {R}_2$ (see Lemma 4.15). There is a general definition of ![]() $\mathrm {Loc}(Y;\mathrm {Sp})^\chi$ for any commutative topological monoid
$\mathrm {Loc}(Y;\mathrm {Sp})^\chi$ for any commutative topological monoid ![]() $H$ acting on a space
$H$ acting on a space ![]() $Y$ and
$Y$ and ![]() $\chi : H\rightarrow \mathrm {Pic}(\mathbf {S})$ an
$\chi : H\rightarrow \mathrm {Pic}(\mathbf {S})$ an ![]() $E_\infty$-map called a character (see Definition 4.14).
$E_\infty$-map called a character (see Definition 4.14).
Consider the map, which is a ![]() $VG_N$-module map (cf. § 4.1.1)
$VG_N$-module map (cf. § 4.1.1)
 \begin{align*} \psi_{N,M} & : VG_N\times Q^0_M\rightarrow \widehat{Q}_{N,M},\\
&\,(A,\mathbf{p}; \mathbf{q},s)\mapsto
(A,\mathbf{q}+2\mathbf{p},s+A(\mathbf{p})),\ \mathbf{p}\in
A, \end{align*}
\begin{align*} \psi_{N,M} & : VG_N\times Q^0_M\rightarrow \widehat{Q}_{N,M},\\
&\,(A,\mathbf{p}; \mathbf{q},s)\mapsto
(A,\mathbf{q}+2\mathbf{p},s+A(\mathbf{p})),\ \mathbf{p}\in
A, \end{align*}
whose stabilization represents the Hamiltonian ![]() $G$-action that sends
$G$-action that sends ![]() $L_0$ to
$L_0$ to ![]() $L_A, A\in G$.
$L_A, A\in G$.
Theorem 1.3 The family of correspondences

induces a canonical equivalence
Intuitively, the theorem states that the ![]() $\varpi _{VG}$-modules in
$\varpi _{VG}$-modules in ![]() $\mathrm {Loc}(\widehat {Q};\mathrm {Sp})$ (as a module of
$\mathrm {Loc}(\widehat {Q};\mathrm {Sp})$ (as a module of ![]() $\mathrm {Loc}(VG;\mathrm {Sp})$) that are freely generated by local systems on
$\mathrm {Loc}(VG;\mathrm {Sp})$) that are freely generated by local systems on ![]() $Q^0$ are characterized precisely as the
$Q^0$ are characterized precisely as the ![]() $J$-equivariant local systems on
$J$-equivariant local systems on ![]() $\widehat {Q}$ (cf. Corollary 4.16 for more details).
$\widehat {Q}$ (cf. Corollary 4.16 for more details).
Now we state an application of the above theorem to stratified Morse theory. Although stratified Morse theory is aimed at constructible sheaves over ordinary rings, there is a direct generalization of it over ring spectra (cf. [Reference Jin and TreumannJT24]). Let ![]() $\mathrm {Shv}_\mathfrak {S}(X;\mathrm {Sp})$ be the full subcategory of
$\mathrm {Shv}_\mathfrak {S}(X;\mathrm {Sp})$ be the full subcategory of ![]() $\mathrm {Shv}(X;\mathrm {Sp})$ consisting of sheaves whose restriction to each stratum
$\mathrm {Shv}(X;\mathrm {Sp})$ consisting of sheaves whose restriction to each stratum ![]() $S_\alpha$ is locally constant. The notion of microlocal stalk can be directly generalized to take values in spectra. Following the notation in § 1.3, we can stabilize
$S_\alpha$ is locally constant. The notion of microlocal stalk can be directly generalized to take values in spectra. Following the notation in § 1.3, we can stabilize ![]() $X$ and
$X$ and ![]() $\mathfrak {S}$ as
$\mathfrak {S}$ as ![]() $X\times \mathbf {R}_{y_1}\times \mathbf {R}_{y_2}\times \cdots$,
$X\times \mathbf {R}_{y_1}\times \mathbf {R}_{y_2}\times \cdots$, ![]() $\{S_\alpha \times \mathbf {R}_{y_1}\times \cdots \}$, and the space of local stratified Morse functions associated to
$\{S_\alpha \times \mathbf {R}_{y_1}\times \cdots \}$, and the space of local stratified Morse functions associated to ![]() $(x,p)$, where
$(x,p)$, where ![]() $x\in S_\beta$ for some
$x\in S_\beta$ for some ![]() $\beta$, can be stabilized by adding
$\beta$, can be stabilized by adding ![]() $-\frac {1}{2}(y_1^2+y_2^2+\cdots )$ in the newly added variables
$-\frac {1}{2}(y_1^2+y_2^2+\cdots )$ in the newly added variables ![]() $y_1,y_2,\ldots$. Then the space of stabilized local stratified Morse functions for
$y_1,y_2,\ldots$. Then the space of stabilized local stratified Morse functions for ![]() $(x,p)$ is canonically homotopy equivalent to
$(x,p)$ is canonically homotopy equivalent to ![]() $G$, through the map taking
$G$, through the map taking ![]() $f$ to the sum of the positive eigenspaces of the Hessian of
$f$ to the sum of the positive eigenspaces of the Hessian of ![]() $f|_{S_\beta \times \mathbf {R}\times \cdots }$ at
$f|_{S_\beta \times \mathbf {R}\times \cdots }$ at ![]() $x$ in
$x$ in ![]() $T_xS_\beta \times \mathbf {R}\times \cdots$. We can view this space as a
$T_xS_\beta \times \mathbf {R}\times \cdots$. We can view this space as a ![]() $G$-torsor in
$G$-torsor in ![]() $\mathcal {S}\mathrm {pc}$.
$\mathcal {S}\mathrm {pc}$.
Theorem 1.4 For any ![]() $\mathcal {F}\in \mathrm {Shv}_{\mathfrak {S}}(X;\mathrm {Sp})$, the process of taking microlocal stalks at
$\mathcal {F}\in \mathrm {Shv}_{\mathfrak {S}}(X;\mathrm {Sp})$, the process of taking microlocal stalks at ![]() $(x,p)\in \Lambda _{\mathfrak {S}}^{\rm sm}$ under stabilization canonically gives rise to a
$(x,p)\in \Lambda _{\mathfrak {S}}^{\rm sm}$ under stabilization canonically gives rise to a ![]() $J$-equivariant local system on the space of stabilized local stratified Morse functions associated to
$J$-equivariant local system on the space of stabilized local stratified Morse functions associated to ![]() $(x,p)$.
$(x,p)$.
Moreover, this builds a canonical equivalence between the microlocal sheaf category associated to a small conic open neighborhood of ![]() $(x,p)$ in
$(x,p)$ in ![]() $\Lambda _\mathfrak {S}^{\rm sm}$ and the category of
$\Lambda _\mathfrak {S}^{\rm sm}$ and the category of ![]() $J$-equivariant local systems of spectra on the space of stabilized local stratified Morse functions associated to
$J$-equivariant local systems of spectra on the space of stabilized local stratified Morse functions associated to ![]() $(x,p)$.
$(x,p)$.
The process of taking microlocal stalks has a natural translation to correspondences via the notion of contact transformations defined in [Reference Kashiwara and SchapiraKS94, A.2]. A contact transformation is just a local conic symplectomorphism that transforms a local piece of conic Lagrangian to another piece of conic Lagrangian, and the local stratified Morse functions correspond to a generic class among them (modulo some obvious equivalences that act trivially on the microlocal stalks), which we call Morse transformations.Footnote 3 These relations are established in §§ 5.1, 5.2, and 5.3. This enables us to reveal the interesting structures underlying the ‘local system of microlocal stalks’ on the space of stabilized local stratified Morse functions, by applying the category of correspondences and using Theorem 1.3. In particular, Theorem 1.4 directly follows from Theorem 5.10. Moreover, there is a generalization of Theorem 1.4 from ![]() $(x,p)\in \Lambda _{\mathfrak {S}}^{\rm sm}$ to the case that
$(x,p)\in \Lambda _{\mathfrak {S}}^{\rm sm}$ to the case that ![]() $(x,p)\in \Lambda ^{\rm sm}$ for any conic Lagrangian
$(x,p)\in \Lambda ^{\rm sm}$ for any conic Lagrangian ![]() $\Lambda$ (see Remark 5.7).
$\Lambda$ (see Remark 5.7).
1.6 Expected strategy of the proof of Claim 1.1
The idea of the proof is easier to express if ![]() $G=\coprod _nBO(n)$ were a group. First let us assume that this were the case. Let
$G=\coprod _nBO(n)$ were a group. First let us assume that this were the case. Let ![]() $L$ be an (immersed) exact Lagrangian in
$L$ be an (immersed) exact Lagrangian in ![]() $T^*\mathbf {R}^N$ and let
$T^*\mathbf {R}^N$ and let ![]() $\mathbf {L}$ be a conic lifting of
$\mathbf {L}$ be a conic lifting of ![]() $L$ in
$L$ in ![]() $T^{*,<0}(\mathbf {R}^N\times \mathbf {R}_t)$. The argument holds for
$T^{*,<0}(\mathbf {R}^N\times \mathbf {R}_t)$. The argument holds for ![]() $L$ being non-exact and can be generalized to the case when
$L$ being non-exact and can be generalized to the case when ![]() $\mathbf {R}^N$ is replaced by a smooth manifold via a standard treatment as in [Reference Abouzaid and KraghAK16]. Now we cover
$\mathbf {R}^N$ is replaced by a smooth manifold via a standard treatment as in [Reference Abouzaid and KraghAK16]. Now we cover ![]() $L$ by small open sets
$L$ by small open sets ![]() $\{\Omega _i\}_{i\in I}$ whose finite intersections are all contractible if not empty (this is called a good cover), which gives a sufficiently fine covering of the front projection of
$\{\Omega _i\}_{i\in I}$ whose finite intersections are all contractible if not empty (this is called a good cover), which gives a sufficiently fine covering of the front projection of ![]() $\mathbf {L}$. In [Reference Jin and TreumannJT24], we show that for each finite intersection
$\mathbf {L}$. In [Reference Jin and TreumannJT24], we show that for each finite intersection ![]() $\bigcap _{s=1}^k\Omega _{i_s}$, the associated microlocal sheaf category with coefficient
$\bigcap _{s=1}^k\Omega _{i_s}$, the associated microlocal sheaf category with coefficient ![]() $\mathbf {S}$ is (non-canonically) equivalent to the
$\mathbf {S}$ is (non-canonically) equivalent to the ![]() $\infty$-category of spectra, which defines a local system of stable
$\infty$-category of spectra, which defines a local system of stable ![]() $\infty$-categories on
$\infty$-categories on ![]() $L$ with fiber equivalent to
$L$ with fiber equivalent to ![]() $\mathrm {Sp}$ denoted by
$\mathrm {Sp}$ denoted by ![]() $\mathrm {Brane}_L$. Such an equivalence of categories follows from the correspondence given by a choice of Morse transformation, and Theorem 1.4 implies that if we consider the Morse transformations altogether (again modulo some obvious equivalences), then the microlocal sheaf category associated to
$\mathrm {Brane}_L$. Such an equivalence of categories follows from the correspondence given by a choice of Morse transformation, and Theorem 1.4 implies that if we consider the Morse transformations altogether (again modulo some obvious equivalences), then the microlocal sheaf category associated to ![]() $\bigcap _{s=1}^k\Omega _i$ is canonically equivalent to the category of
$\bigcap _{s=1}^k\Omega _i$ is canonically equivalent to the category of ![]() $J$-equivariant local systems of spectra on the space of Morse transformations associated to
$J$-equivariant local systems of spectra on the space of Morse transformations associated to ![]() $\bigcap _{s=1}^k\Omega _i$ which is a
$\bigcap _{s=1}^k\Omega _i$ which is a ![]() $G$-torsor.
$G$-torsor.
Let ![]() $\check {C}_\bullet L$ be the
$\check {C}_\bullet L$ be the ![]() $\check {\text {C}}$ech nerve of the covering
$\check {\text {C}}$ech nerve of the covering ![]() $\{\Omega _i\}_{i\in I}$, and let
$\{\Omega _i\}_{i\in I}$, and let ![]() $G\text {-}\mathsf {torsors}$ denote the
$G\text {-}\mathsf {torsors}$ denote the ![]() $E_\infty$-groupoid of
$E_\infty$-groupoid of ![]() $G$-torsors in
$G$-torsors in ![]() $\mathcal {S}\mathrm {pc}$, which is equivalent to
$\mathcal {S}\mathrm {pc}$, which is equivalent to ![]() $BG$ (assuming
$BG$ (assuming ![]() $G$ were a group). The above implies that the classifying map for
$G$ were a group). The above implies that the classifying map for ![]() $\mathrm {Brane}_L$ factors as
$\mathrm {Brane}_L$ factors as
where the first map ![]() $\check {\gamma }$ is taking the space of Morse transformations and the latter is taking a
$\check {\gamma }$ is taking the space of Morse transformations and the latter is taking a ![]() $G$-torsor
$G$-torsor ![]() $M$ to
$M$ to ![]() $\mathrm {Loc}(M;\mathrm {Sp})^J$. Here we use a compatibility result of Morse transformations under the restriction from a small open set to a smaller one in the
$\mathrm {Loc}(M;\mathrm {Sp})^J$. Here we use a compatibility result of Morse transformations under the restriction from a small open set to a smaller one in the ![]() $\check {\text {C}}$ech cover. One can show that
$\check {\text {C}}$ech cover. One can show that ![]() $\check {\gamma }$ is homotopic to the stable Gauss map after passing to the geometric realization
$\check {\gamma }$ is homotopic to the stable Gauss map after passing to the geometric realization ![]() $|\check {C}_\bullet L|\simeq L$, and
$|\check {C}_\bullet L|\simeq L$, and ![]() $\mathrm {Loc}(-;\mathrm {Sp})^J$ exactly models the delooping of the
$\mathrm {Loc}(-;\mathrm {Sp})^J$ exactly models the delooping of the ![]() $J$-homomorphism (up to the canonical involution on
$J$-homomorphism (up to the canonical involution on ![]() $BG$). This proves Claim 1.1 under the assumption that
$BG$). This proves Claim 1.1 under the assumption that ![]() $G$ were a group.
$G$ were a group.
For the actual situation in which ![]() $G=\coprod _nBO(n)$ is not a group, some more work needs to be done, which involves a more detailed study of the space
$G=\coprod _nBO(n)$ is not a group, some more work needs to be done, which involves a more detailed study of the space ![]() $U/O$ and the compatibility of Morse transformations under restrictions (see § 5.6). For example, one technical step in [Reference JinJin20] is to replace the universal principal
$U/O$ and the compatibility of Morse transformations under restrictions (see § 5.6). For example, one technical step in [Reference JinJin20] is to replace the universal principal ![]() $\mathbf {Z}\times BO$-bundle
$\mathbf {Z}\times BO$-bundle ![]() $E(\mathbf {Z}\times BO)\to U/O$ by an
$E(\mathbf {Z}\times BO)\to U/O$ by an ![]() $\infty$-category of quadruples
$\infty$-category of quadruples ![]() $(\mathcal {U}, Q_\flat,\,{}^{\backprime }{G}, M)$, denoted by
$(\mathcal {U}, Q_\flat,\,{}^{\backprime }{G}, M)$, denoted by ![]() $\mathsf {QHam}(U/O)$, over
$\mathsf {QHam}(U/O)$, over ![]() $\mathrm {Open}(U/O)^{\rm op}$, where
$\mathrm {Open}(U/O)^{\rm op}$, where ![]() $\mathcal {U}$ is an open subset of
$\mathcal {U}$ is an open subset of ![]() $U/O$,
$U/O$, ![]() $Q_\flat$ is a (stabilized) quadratic form that plays a similar role as
$Q_\flat$ is a (stabilized) quadratic form that plays a similar role as ![]() $A_S$ in (5.4.2) with
$A_S$ in (5.4.2) with ![]() $T_{(0,0)}L$ replaced by
$T_{(0,0)}L$ replaced by ![]() $\ell \in \mathcal {U}$,
$\ell \in \mathcal {U}$, ![]() $^{\backprime }{G}$ is a commutative algebra object in
$^{\backprime }{G}$ is a commutative algebra object in ![]() $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})$ (see § 1.7 below) that plays a similar role as
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})$ (see § 1.7 below) that plays a similar role as ![]() $G$ (or
$G$ (or ![]() $G^{A^\perp }$ (5.6.1) depending on the choice of
$G^{A^\perp }$ (5.6.1) depending on the choice of ![]() $A_S$), and
$A_S$), and ![]() $M$ is a free module of
$M$ is a free module of ![]() $^{\backprime }{G}$ generated by
$^{\backprime }{G}$ generated by ![]() $Q_\flat$ (parametrizing a space of Morse transformations that work for all
$Q_\flat$ (parametrizing a space of Morse transformations that work for all ![]() $\ell \in \mathcal {U}$). A morphism between two objects
$\ell \in \mathcal {U}$). A morphism between two objects ![]() $(\mathcal {U}_i, Q^{(i)}_\flat$,
$(\mathcal {U}_i, Q^{(i)}_\flat$, ![]() $^{\backprime }{G}_{(i)}, M_{(i)})$ is roughly given by
$^{\backprime }{G}_{(i)}, M_{(i)})$ is roughly given by ![]() $\mathcal {U}_2\hookrightarrow \mathcal {U}_1$, an inclusion
$\mathcal {U}_2\hookrightarrow \mathcal {U}_1$, an inclusion ![]() $^{\backprime }{G}_{(1)}\hookrightarrow \,{}^{\backprime }{G}_{(2)}$ that is a commutative algebra homomorphism, and a
$^{\backprime }{G}_{(1)}\hookrightarrow \,{}^{\backprime }{G}_{(2)}$ that is a commutative algebra homomorphism, and a ![]() $^{\backprime }{G}_{(1)}$-module map
$^{\backprime }{G}_{(1)}$-module map ![]() $M_{(1)}\hookrightarrow M_{(2)}$ that sends
$M_{(1)}\hookrightarrow M_{(2)}$ that sends ![]() $Q_\flat ^{(1)}$ to some appropriate element in
$Q_\flat ^{(1)}$ to some appropriate element in ![]() $M_{(2)}$. The key point of introducing
$M_{(2)}$. The key point of introducing ![]() $\mathsf {QHam}(U/O)$ is that the quantization results contained in this paper will be assembled into a natural functor
$\mathsf {QHam}(U/O)$ is that the quantization results contained in this paper will be assembled into a natural functor ![]() $F: \mathsf {QHam}(U/O)\to \mathrm {Fun}(\Delta ^1, \mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$ that sends
$F: \mathsf {QHam}(U/O)\to \mathrm {Fun}(\Delta ^1, \mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$ that sends ![]() $(\mathcal {U}, Q_\flat, \,{}^{\backprime }{G}, M)$ to an equivalence of categories analogous to that in Theorem 1.3 (more precisely, see [Reference JinJin20, Proposition 4.13]), and it further induces a functor
$(\mathcal {U}, Q_\flat, \,{}^{\backprime }{G}, M)$ to an equivalence of categories analogous to that in Theorem 1.3 (more precisely, see [Reference JinJin20, Proposition 4.13]), and it further induces a functor ![]() $\mathrm {Open}(U/O)^{\rm op}\to \mathrm {Fun}(\Delta ^1, \mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$ by right Kan extension. To give an appropriate definition of
$\mathrm {Open}(U/O)^{\rm op}\to \mathrm {Fun}(\Delta ^1, \mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$ by right Kan extension. To give an appropriate definition of ![]() $\mathsf {QHam}(U/O)$ that works for our purposes, we must allow
$\mathsf {QHam}(U/O)$ that works for our purposes, we must allow ![]() $Q_\flat$ and
$Q_\flat$ and ![]() $^{\backprime }{G}$ to be more flexible than
$^{\backprime }{G}$ to be more flexible than ![]() $A_S$ and
$A_S$ and ![]() $G^{A^\perp }$ that are considered in § 5.6. For example, since our
$G^{A^\perp }$ that are considered in § 5.6. For example, since our ![]() $\ell$ is moving in
$\ell$ is moving in ![]() $\mathcal {U}$, we cannot expect (5.4.2) to hold for all
$\mathcal {U}$, we cannot expect (5.4.2) to hold for all ![]() $\ell \in \mathcal {U}$. There are other more subtle reasons that impose both flexibility and technical conditions on
$\ell \in \mathcal {U}$. There are other more subtle reasons that impose both flexibility and technical conditions on ![]() $Q_\flat$,
$Q_\flat$, ![]() $^{\backprime }{G}$ and the morphisms between the objects in
$^{\backprime }{G}$ and the morphisms between the objects in ![]() $\mathsf {QHam}(U/O)$ (cf. [Reference JinJin20, § 4.1]).
$\mathsf {QHam}(U/O)$ (cf. [Reference JinJin20, § 4.1]).
In the following, we give a brief overview of the category of correspondences, the results we have obtained and how we apply these results to the quantization process.
1.7 The category of correspondences and the functor of taking sheaves of spectra
For any ordinary 1-category ![]() $\mathcal {C}$ that admits fiber products, one can define an ordinary 2-category
$\mathcal {C}$ that admits fiber products, one can define an ordinary 2-category ![]() $\mathbf {Corr}(\mathcal {C})$ (cf. [Reference Gaitsgory and RozenblyumGR17]) with the same objects as
$\mathbf {Corr}(\mathcal {C})$ (cf. [Reference Gaitsgory and RozenblyumGR17]) with the same objects as ![]() $\mathcal {C}$ and whose set of morphisms from an object
$\mathcal {C}$ and whose set of morphisms from an object ![]() $X$ to
$X$ to ![]() $Y$ consists of correspondences
$Y$ consists of correspondences

A 2-morphism between 1-morphisms is presented by the left one of the following commutative diagrams (
1.7.2), and a composition of two 1-morphisms is presented by the outer correspondence on the right.

There is a higher categorical analogue of this where ![]() $\mathcal {C}$ is an
$\mathcal {C}$ is an ![]() $\infty$-category and
$\infty$-category and ![]() $\mathbf {Corr}(\mathcal {C})$ is an
$\mathbf {Corr}(\mathcal {C})$ is an ![]() $(\infty,2)$-category. One can also forget the non-invertible 2-morphisms, and get an
$(\infty,2)$-category. One can also forget the non-invertible 2-morphisms, and get an ![]() $\infty$-category
$\infty$-category ![]() $\mathrm {Corr}(\mathcal {C})$. If
$\mathrm {Corr}(\mathcal {C})$. If ![]() $\mathcal {C}$ is (symmetric) monoidal, then
$\mathcal {C}$ is (symmetric) monoidal, then ![]() $\mathbf {Corr}(\mathcal {C})$ is (symmetric) monoidal, and so is
$\mathbf {Corr}(\mathcal {C})$ is (symmetric) monoidal, and so is ![]() $\mathrm {Corr}(\mathcal {C})$.
$\mathrm {Corr}(\mathcal {C})$.
In [Reference Gaitsgory and RozenblyumGR17], the authors introduce the ![]() $(\infty,2)$-category of correspondences and use it to give a systematic treatment of the six-functor formalism for dg-categories of quasi/ind-coherent sheaves. A similar treatment without using
$(\infty,2)$-category of correspondences and use it to give a systematic treatment of the six-functor formalism for dg-categories of quasi/ind-coherent sheaves. A similar treatment without using ![]() $(\infty,2)$-categories has been taken in [Reference Liu and ZhengLZ12]. The approach of [Reference Gaitsgory and RozenblyumGR17] can be adapted to the case of sheaves of spectra, given the foundations on
$(\infty,2)$-categories has been taken in [Reference Liu and ZhengLZ12]. The approach of [Reference Gaitsgory and RozenblyumGR17] can be adapted to the case of sheaves of spectra, given the foundations on ![]() $\infty$-topoi [Reference LurieLur09] and stable
$\infty$-topoi [Reference LurieLur09] and stable ![]() $\infty$-categories [Reference LurieLur17]. Let
$\infty$-categories [Reference LurieLur17]. Let ![]() $\mathrm {S}_{\mathrm {LCH}}$ be the ordinary 1-category of locally compact Hausdorff spaces, equipped with the Cartesian symmetric monoidal structure, i.e. the tensor product is just the Cartesian product. The starting point is the symmetric monoidal functor (cf. [Reference LurieLur09])
$\mathrm {S}_{\mathrm {LCH}}$ be the ordinary 1-category of locally compact Hausdorff spaces, equipped with the Cartesian symmetric monoidal structure, i.e. the tensor product is just the Cartesian product. The starting point is the symmetric monoidal functor (cf. [Reference LurieLur09])
 \begin{align*}
\mathrm{Shv}\mathcal{S}:\ &(\mathrm{S}_{\mathrm{LCH}})^{\rm op}\rightarrow
\mathcal{P}\mathrm{r}^{\mathrm{L}}\\ & X\mapsto
\mathrm{Shv}(X;\mathcal{S})\\ &(f: X\rightarrow Y)\mapsto
(f^*:
\mathrm{Shv}(Y;\mathcal{S})\rightarrow\mathrm{Shv}(X;\mathcal{S})),
\end{align*}
\begin{align*}
\mathrm{Shv}\mathcal{S}:\ &(\mathrm{S}_{\mathrm{LCH}})^{\rm op}\rightarrow
\mathcal{P}\mathrm{r}^{\mathrm{L}}\\ & X\mapsto
\mathrm{Shv}(X;\mathcal{S})\\ &(f: X\rightarrow Y)\mapsto
(f^*:
\mathrm{Shv}(Y;\mathcal{S})\rightarrow\mathrm{Shv}(X;\mathcal{S})),
\end{align*}
where ![]() $\mathrm {Shv}(X;\mathcal {S})$ denotes the (presentable)
$\mathrm {Shv}(X;\mathcal {S})$ denotes the (presentable) ![]() $\infty$-category of sheaves of spaces on
$\infty$-category of sheaves of spaces on ![]() $X$ and
$X$ and ![]() $\mathcal {P}\mathrm {r}^{\mathrm {L}}$ denotes the
$\mathcal {P}\mathrm {r}^{\mathrm {L}}$ denotes the ![]() $\infty$-category of presentable
$\infty$-category of presentable ![]() $\infty$-categories with continuous functors. Taking stabilizations of
$\infty$-categories with continuous functors. Taking stabilizations of ![]() $\mathrm {Shv}(X;\mathcal {S})$ to
$\mathrm {Shv}(X;\mathcal {S})$ to ![]() $\mathrm {Shv}(X;\mathrm {Sp})$ and running the approach in [Reference Gaitsgory and RozenblyumGR17], one gets all six functors, and one has the following statement that is crucial for our purposes mentioned above.
$\mathrm {Shv}(X;\mathrm {Sp})$ and running the approach in [Reference Gaitsgory and RozenblyumGR17], one gets all six functors, and one has the following statement that is crucial for our purposes mentioned above.
Theorem 1.5 There is a canonical symmetric monoidal functor
sending ![]() $X$ to
$X$ to ![]() $\mathrm {Shv}(X;\mathrm {Sp})$ and any correspondence (1.7.1) to the functor
$\mathrm {Shv}(X;\mathrm {Sp})$ and any correspondence (1.7.1) to the functor ![]() $g_!f^*: \mathrm {Shv}(X;\mathrm {Sp})\rightarrow \mathrm {Shv}(Y;\mathrm {Sp})$.
$g_!f^*: \mathrm {Shv}(X;\mathrm {Sp})\rightarrow \mathrm {Shv}(Y;\mathrm {Sp})$.
Here ![]() $\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$ is the
$\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$ is the ![]() $\infty$-category of presentable stable
$\infty$-category of presentable stable ![]() $\infty$-categories. The theorem will be proved in § 3. Now to define a symmetric monoidal structure on
$\infty$-categories. The theorem will be proved in § 3. Now to define a symmetric monoidal structure on ![]() $\mathrm {Shv}(X;\mathrm {Sp})$ for some
$\mathrm {Shv}(X;\mathrm {Sp})$ for some ![]() $X\in \mathrm {S}_{\mathrm {LCH}}$, it suffices to endow
$X\in \mathrm {S}_{\mathrm {LCH}}$, it suffices to endow ![]() $X$ with the structure of a commutative algebra object in
$X$ with the structure of a commutative algebra object in ![]() $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})$. This is exactly the motivation for us to develop general and concrete constructions of (commutative) algebra objects in § 2, together with their modules, (right-lax) homomorphisms between algebras, etc. in
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})$. This is exactly the motivation for us to develop general and concrete constructions of (commutative) algebra objects in § 2, together with their modules, (right-lax) homomorphisms between algebras, etc. in ![]() $\mathbf {Corr}(\mathcal {C})$, for a Cartesian symmetric monoidal
$\mathbf {Corr}(\mathcal {C})$, for a Cartesian symmetric monoidal ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$.
$\mathcal {C}$.
Let ![]() $\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {R}}\simeq (\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})^{\rm op}$ be the
$\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {R}}\simeq (\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})^{\rm op}$ be the ![]() $\infty$-category of presentable stable
$\infty$-category of presentable stable ![]() $\infty$-categories with limit preserving functors. There is a canonical identification
$\infty$-categories with limit preserving functors. There is a canonical identification ![]() $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})\simeq \mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})^{\rm op}$ by flipping the correspondences (cf. [Reference Gaitsgory and RozenblyumGR17, Chapter 9, 2.2]). Hence, by taking opposite categories on the source and target of
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})\simeq \mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})^{\rm op}$ by flipping the correspondences (cf. [Reference Gaitsgory and RozenblyumGR17, Chapter 9, 2.2]). Hence, by taking opposite categories on the source and target of ![]() $\mathrm {ShvSp}$, we get the following.
$\mathrm {ShvSp}$, we get the following.
Corollary 1.6 There is a canonical symmetric monoidal functor
sending ![]() $X$ to
$X$ to ![]() $\mathrm {Shv}(X;\mathrm {Sp})$ and any correspondence (1.7.1) to the functor
$\mathrm {Shv}(X;\mathrm {Sp})$ and any correspondence (1.7.1) to the functor ![]() $g_*f^!: \mathrm {Shv}(X;\mathrm {Sp})\rightarrow \mathrm {Shv}(Y;\mathrm {Sp})$.
$g_*f^!: \mathrm {Shv}(X;\mathrm {Sp})\rightarrow \mathrm {Shv}(Y;\mathrm {Sp})$.
Remark 1.7 (i) For any ![]() $X\in \mathrm {S}_{\mathrm {LCH}}$, let
$X\in \mathrm {S}_{\mathrm {LCH}}$, let ![]() $\mathrm {Loc}(X;\mathrm {Sp})$ be the category of locally constant cosheaves on
$\mathrm {Loc}(X;\mathrm {Sp})$ be the category of locally constant cosheaves on ![]() $X$ (also referred as local systems). Let
$X$ (also referred as local systems). Let ![]() $\mathrm {Loc}'(X;\mathrm {Sp})$ be the category of locally constant sheaves on
$\mathrm {Loc}'(X;\mathrm {Sp})$ be the category of locally constant sheaves on ![]() $X$. The former is identified, via the Verdier duality functor, with the full subcategory of
$X$. The former is identified, via the Verdier duality functor, with the full subcategory of ![]() $\mathrm {Shv}(X;\mathrm {Sp})$ consisting of
$\mathrm {Shv}(X;\mathrm {Sp})$ consisting of ![]() $\mathcal {F}$ with
$\mathcal {F}$ with ![]() $\Gamma _c(-,\mathcal {F})$ locally constant. For a smooth manifold
$\Gamma _c(-,\mathcal {F})$ locally constant. For a smooth manifold ![]() $X$,
$X$, ![]() $\mathrm {Loc}(X;\mathrm {Sp})$ is identified with
$\mathrm {Loc}(X;\mathrm {Sp})$ is identified with ![]() $\mathrm {Loc}'(X;\mathrm {Sp})$. Throughout the paper, the spaces in
$\mathrm {Loc}'(X;\mathrm {Sp})$. Throughout the paper, the spaces in ![]() $\mathrm {S}_{\mathrm {LCH}}$ that we are dealing with are smooth, e.g.
$\mathrm {S}_{\mathrm {LCH}}$ that we are dealing with are smooth, e.g. ![]() $G_N, VG_N$, so we will not distinguish between
$G_N, VG_N$, so we will not distinguish between ![]() $\mathrm {Loc}$ and
$\mathrm {Loc}$ and ![]() $\mathrm {Loc}'$ for them.Footnote 4
$\mathrm {Loc}'$ for them.Footnote 4
(ii) The preference for locally constant cosheaves over locally constant sheaves emerges naturally. First, in § 3 and a good portion of § 4, we are dealing with sheaf categories (not just local system categories), and we later focus on ![]() $\mathrm {Shv}(VG;\mathrm {Sp})$ and
$\mathrm {Shv}(VG;\mathrm {Sp})$ and ![]() $\mathrm {Shv}(G;\mathrm {Sp})$ (and a few others) which are defined, in the standard way, as the colimit categories of
$\mathrm {Shv}(G;\mathrm {Sp})$ (and a few others) which are defined, in the standard way, as the colimit categories of ![]() $\mathrm {Shv}(VG_N;\mathrm {Sp})$ and
$\mathrm {Shv}(VG_N;\mathrm {Sp})$ and ![]() $\mathrm {Shv}(G_N;\mathrm {Sp})$ over
$\mathrm {Shv}(G_N;\mathrm {Sp})$ over ![]() $N\in \mathbf {Z}_{\geq 0}$ in
$N\in \mathbf {Z}_{\geq 0}$ in ![]() $\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$, respectively, through
$\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$, respectively, through ![]() $!$-pushforward (equivalently
$!$-pushforward (equivalently ![]() $*$-pushforward since all inclusions are proper) for the sequence of inclusions (1.2.2). It is well known that these colimit categories are equivalent to the limit category
$*$-pushforward since all inclusions are proper) for the sequence of inclusions (1.2.2). It is well known that these colimit categories are equivalent to the limit category ![]() $\varprojlim _{N}\mathrm {Shv}(VG_N;\mathrm {Sp})$ and
$\varprojlim _{N}\mathrm {Shv}(VG_N;\mathrm {Sp})$ and ![]() $\varprojlim _{N}\mathrm {Shv}(G_N;\mathrm {Sp})$ in
$\varprojlim _{N}\mathrm {Shv}(G_N;\mathrm {Sp})$ in ![]() $\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {R}}$, respectively, through
$\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {R}}$, respectively, through ![]() $!$-pullbacks (by taking the right adjoints), and the latter is much easier to calculate since the limits are equivalently taken in
$!$-pullbacks (by taking the right adjoints), and the latter is much easier to calculate since the limits are equivalently taken in ![]() $1\text {-}\mathcal {C}\mathrm {at}$. Under this setting, we have the dualizing sheaf
$1\text {-}\mathcal {C}\mathrm {at}$. Under this setting, we have the dualizing sheaf ![]() $\varpi _{VG}$ (respectively,
$\varpi _{VG}$ (respectively, ![]() $\varpi _G$), rather than the constant sheaf, as a well-defined object in
$\varpi _G$), rather than the constant sheaf, as a well-defined object in ![]() $\mathrm {Shv}(VG;\mathrm {Sp})$ (respectively,
$\mathrm {Shv}(VG;\mathrm {Sp})$ (respectively, ![]() $\mathrm {Shv}(G;\mathrm {Sp})$) and as the monoidal unit of
$\mathrm {Shv}(G;\mathrm {Sp})$) and as the monoidal unit of ![]() $\overset {!}{\otimes }$ on
$\overset {!}{\otimes }$ on ![]() $\mathrm {Shv}(VG;\mathrm {Sp})$ (respectively,
$\mathrm {Shv}(VG;\mathrm {Sp})$ (respectively, ![]() $\mathrm {Shv}(G;\mathrm {Sp})$). Second, it is convenient to characterize the dualizing sheaf
$\mathrm {Shv}(G;\mathrm {Sp})$). Second, it is convenient to characterize the dualizing sheaf ![]() $\varpi _X$ as the constant cosheaf with costalk
$\varpi _X$ as the constant cosheaf with costalk ![]() $\mathbf {S}$. In particular, the
$\mathbf {S}$. In particular, the ![]() $!$-pullback functors on sheaves are quite explicit using the cosheaf perspective.
$!$-pullback functors on sheaves are quite explicit using the cosheaf perspective.
(iii) In summary, the six functors that we consider are all for sheaves (we do not consider operations separately for cosheaves). On the other hand, the cosheaf perspective gives a convenient way to describe certain sheaves in ![]() $\mathrm {Shv}(VG;\mathrm {Sp})$, e.g.
$\mathrm {Shv}(VG;\mathrm {Sp})$, e.g. ![]() $\varpi _{VG}$, and makes the
$\varpi _{VG}$, and makes the ![]() $!$-pullback functors much more explicit. Furthermore, this offers us a convenient transition from viewing
$!$-pullback functors much more explicit. Furthermore, this offers us a convenient transition from viewing ![]() $!$-pullback between
$!$-pullback between ![]() $\mathrm {Loc}(X;\mathrm {Sp})$ for maps inside
$\mathrm {Loc}(X;\mathrm {Sp})$ for maps inside ![]() $\mathrm {S}_{\mathrm {LCH}}$ to
$\mathrm {S}_{\mathrm {LCH}}$ to ![]() $!$-pullback between
$!$-pullback between ![]() $\mathrm {Loc}(X;\mathrm {Sp})$ for the corresponding homotopy classes of maps insideFootnote 5
$\mathrm {Loc}(X;\mathrm {Sp})$ for the corresponding homotopy classes of maps insideFootnote 5 ![]() $\mathcal {S}\mathrm {pc}$ (which is, for example, needed for our formulation of the
$\mathcal {S}\mathrm {pc}$ (which is, for example, needed for our formulation of the ![]() $J$-homomorphism). The latter makes sense by identifying
$J$-homomorphism). The latter makes sense by identifying ![]() $\mathrm {Loc}(X;\mathrm {Sp})$ with
$\mathrm {Loc}(X;\mathrm {Sp})$ with ![]() $\mathrm {Fun}(X, \mathrm {Sp})$ (so then it becomes the standard pullback functor), and it has a left adjoint, denoted as
$\mathrm {Fun}(X, \mathrm {Sp})$ (so then it becomes the standard pullback functor), and it has a left adjoint, denoted as ![]() $!$-pushforward between local systems.
$!$-pushforward between local systems.
Now let
 \begin{align} (\mathrm{Loc})^!_*: \mathrm{Corr}(\mathrm{S}_{\mathrm{LCH}})_{\mathsf{fib}, \mathsf{all}}&\rightarrow \mathcal{P}\mathrm{r}_{\mathrm{st}}^{\mathrm{L}},\\ X&\mapsto \mathrm{Loc}(X;\mathrm{Sp}) \nonumber \end{align}
\begin{align} (\mathrm{Loc})^!_*: \mathrm{Corr}(\mathrm{S}_{\mathrm{LCH}})_{\mathsf{fib}, \mathsf{all}}&\rightarrow \mathcal{P}\mathrm{r}_{\mathrm{st}}^{\mathrm{L}},\\ X&\mapsto \mathrm{Loc}(X;\mathrm{Sp}) \nonumber \end{align}
be the functor induced from ![]() $\mathrm {ShvSp}^!_*$, which restricts the vertical arrows in correspondences to locally trivial fibrations and takes each
$\mathrm {ShvSp}^!_*$, which restricts the vertical arrows in correspondences to locally trivial fibrations and takes each ![]() $X$ to the full subcategory of locally constant cosheaves. Note that here we can write the target as
$X$ to the full subcategory of locally constant cosheaves. Note that here we can write the target as ![]() $\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$ instead of
$\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$ instead of ![]() $\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {R}}$, since all the functors involved are continuous. In our applications, we will mainly use the functor
$\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {R}}$, since all the functors involved are continuous. In our applications, we will mainly use the functor ![]() $\mathrm {Loc}^!_*$, which is symmetric monoidal. Then (as mentioned before), the limit (1.2.3) and (1.2.5) are taken with respect to
$\mathrm {Loc}^!_*$, which is symmetric monoidal. Then (as mentioned before), the limit (1.2.3) and (1.2.5) are taken with respect to ![]() $!$-pullbacks.
$!$-pullbacks.
1.8 Applications of the category of correspondences to quantizations
For simplicity, we only explain the application of correspondences to define the symmetric monoidal convolution structure on ![]() $\mathrm {Loc}(VG;\mathrm {Sp})$ and the module structure on
$\mathrm {Loc}(VG;\mathrm {Sp})$ and the module structure on ![]() $\mathrm {Loc}(\widehat {Q};\mathrm {Sp})$. Other applications follow from a similar line of ideas. In order to apply the functor
$\mathrm {Loc}(\widehat {Q};\mathrm {Sp})$. Other applications follow from a similar line of ideas. In order to apply the functor ![]() $\mathrm {Loc}_*^!$ whose source is
$\mathrm {Loc}_*^!$ whose source is ![]() $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$, we need to first work with
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$, we need to first work with ![]() $VG_N$ and
$VG_N$ and ![]() $\widehat {Q}_{N,M}$ and then show the compatibility of the structures with taking limit over
$\widehat {Q}_{N,M}$ and then show the compatibility of the structures with taking limit over ![]() $N$ and
$N$ and ![]() $(N,M)$, respectively. In fact, using our approach we can show that the symmetric monoidal structure and module structure already exist at finite levels, i.e. on
$(N,M)$, respectively. In fact, using our approach we can show that the symmetric monoidal structure and module structure already exist at finite levels, i.e. on ![]() $\mathrm {Loc}(VG_N;\mathrm {Sp})$ and
$\mathrm {Loc}(VG_N;\mathrm {Sp})$ and ![]() $\mathrm {Loc}(\widehat {Q}_{N,M};\mathrm {Sp})$, respectively.
$\mathrm {Loc}(\widehat {Q}_{N,M};\mathrm {Sp})$, respectively.
The convolution structures at finite levels come from the following correspondences

where: (i) ![]() $\iota _{N}$ is the embedding of the subvariety of pairs
$\iota _{N}$ is the embedding of the subvariety of pairs ![]() $(A_1,\mathbf {p}_1;A_2,\mathbf {p}_2), \mathbf {p}_i\in A_i$ where
$(A_1,\mathbf {p}_1;A_2,\mathbf {p}_2), \mathbf {p}_i\in A_i$ where ![]() $A_1\perp A_2$, and
$A_1\perp A_2$, and ![]() $a_{N}$ is the natural addition
$a_{N}$ is the natural addition ![]() $(A_1\oplus A_2, \mathbf {p}_1+\mathbf {p}_2)$; (ii)
$(A_1\oplus A_2, \mathbf {p}_1+\mathbf {p}_2)$; (ii) ![]() $\jmath _{N,M}$ is defined similarly as
$\jmath _{N,M}$ is defined similarly as ![]() $\iota _N$ and
$\iota _N$ and
The structure functors are given by
 \begin{gather*}
(a_{N})_*\iota_{N}^!\circ\boxtimes:\mathrm{Loc}(VG_N;\mathrm{Sp})\otimes
\mathrm{Loc}(VG_N;\mathrm{Sp})\rightarrow
\mathrm{Loc}(VG_N;\mathrm{Sp}), \\
(a_{N,M})_*\jmath_{N,M}^!\circ\boxtimes:
\mathrm{Loc}(VG_N;\mathrm{Sp})\otimes
\mathrm{Loc}(\widehat{Q}_{N,M})\rightarrow
\mathrm{Loc}(\widehat{Q}_{N,M}). \end{gather*}
\begin{gather*}
(a_{N})_*\iota_{N}^!\circ\boxtimes:\mathrm{Loc}(VG_N;\mathrm{Sp})\otimes
\mathrm{Loc}(VG_N;\mathrm{Sp})\rightarrow
\mathrm{Loc}(VG_N;\mathrm{Sp}), \\
(a_{N,M})_*\jmath_{N,M}^!\circ\boxtimes:
\mathrm{Loc}(VG_N;\mathrm{Sp})\otimes
\mathrm{Loc}(\widehat{Q}_{N,M})\rightarrow
\mathrm{Loc}(\widehat{Q}_{N,M}). \end{gather*}
However, to give a precise definition of the symmetric monoidal structure on ![]() $\mathrm {Loc}(VG;\mathrm {Sp})$ and the module structure on
$\mathrm {Loc}(VG;\mathrm {Sp})$ and the module structure on ![]() $\mathrm {Loc}(\widehat {Q};\mathrm {Sp})$, it is not enough to just list the functors above: there are coherent homotopies that encode the commutativity and associativity properties and their compatibility with taking limit, which is an infinite amount of data.
$\mathrm {Loc}(\widehat {Q};\mathrm {Sp})$, it is not enough to just list the functors above: there are coherent homotopies that encode the commutativity and associativity properties and their compatibility with taking limit, which is an infinite amount of data.
The category of correspondences is an ideal tool to resolve the above issues. The upshot is that all the homotopy coherence data can be packaged inside the category of correspondences where things can be checked on the nose. For example, to present the desired symmetric monoidal structure on ![]() $\mathrm {Loc}(VG_N;\mathrm {Sp})$, we can construct a commutative algebra object in
$\mathrm {Loc}(VG_N;\mathrm {Sp})$, we can construct a commutative algebra object in ![]() $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$ whose underlying object is
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$ whose underlying object is ![]() $VG_N$ and whose multiplication rule is given by (1.8.1). To show that the inclusion
$VG_N$ and whose multiplication rule is given by (1.8.1). To show that the inclusion ![]() $\iota _{N,N'}: VG_N\hookrightarrow VG_{N'}$,
$\iota _{N,N'}: VG_N\hookrightarrow VG_{N'}$, ![]() $N'\geq N$ induces a symmetric monoidal functor
$N'\geq N$ induces a symmetric monoidal functor ![]() $\iota _{N,N'}^!: \mathrm {Loc}(VG_{N'};\mathrm {Sp})\rightarrow \mathrm {Loc}(VG_N;\mathrm {Sp})$, we just need to show that
$\iota _{N,N'}^!: \mathrm {Loc}(VG_{N'};\mathrm {Sp})\rightarrow \mathrm {Loc}(VG_N;\mathrm {Sp})$, we just need to show that ![]() $\iota _{N,N'}$ can be upgraded to an algebra homomorphism from
$\iota _{N,N'}$ can be upgraded to an algebra homomorphism from ![]() $VG_{N'}$ to
$VG_{N'}$ to ![]() $VG_N$ as commutative algebra objects. In view of the following theorem (stated informally), these can be encoded by discrete data.
$VG_N$ as commutative algebra objects. In view of the following theorem (stated informally), these can be encoded by discrete data.
Let ![]() $\mathrm {Fin}_*$ denote the ordinary 1-category of pointed finite sets, where any morphism between two pointed sets preserves the marked point.
$\mathrm {Fin}_*$ denote the ordinary 1-category of pointed finite sets, where any morphism between two pointed sets preserves the marked point.
Theorem 1.8 Let ![]() $\mathcal {C}$ be an
$\mathcal {C}$ be an ![]() $\infty$-category endowed with the Cartesian symmetric monoidal structure.
$\infty$-category endowed with the Cartesian symmetric monoidal structure.
(a) Any simplicial object (respectively,
 $\mathrm {Fin}_*$-object)
$\mathrm {Fin}_*$-object)  $C^\bullet$ in
$C^\bullet$ in  $\mathcal {C}$ naturally determines an associative (respectively, commutative) algebra object in
$\mathcal {C}$ naturally determines an associative (respectively, commutative) algebra object in  $\mathrm {Corr}(\mathcal {C})$ if a prescribed class of diagrams are Cartesian in
$\mathrm {Corr}(\mathcal {C})$ if a prescribed class of diagrams are Cartesian in  $\mathcal {C}$.
$\mathcal {C}$.(b) Let
 $C^\bullet, W^\bullet, D^\bullet$ be simplicial objects (respectively,
$C^\bullet, W^\bullet, D^\bullet$ be simplicial objects (respectively,  $\mathrm {Fin}_*$-objects) in
$\mathrm {Fin}_*$-objects) in  $\mathcal {C}$ that satisfy the condition in part (a). Any correspondence
naturally induces a (right-lax) homomorphism from the associative (respectively, commutative) algebra object corresponding to
$\mathcal {C}$ that satisfy the condition in part (a). Any correspondence
naturally induces a (right-lax) homomorphism from the associative (respectively, commutative) algebra object corresponding to
 $C^\bullet$ to that corresponding to
$C^\bullet$ to that corresponding to  $D^\bullet$ in
$D^\bullet$ in  $\mathbf {Corr}(\mathcal {C})$ if a prescribed class of diagrams are Cartesian in
$\mathbf {Corr}(\mathcal {C})$ if a prescribed class of diagrams are Cartesian in  $\mathcal {C}$, respectively.
$\mathcal {C}$, respectively.
Indeed, we construct ![]() $\mathrm {Fin}_*$-objects
$\mathrm {Fin}_*$-objects ![]() $VG_N^\bullet$ and morphisms
$VG_N^\bullet$ and morphisms ![]() $VG_N^\bullet \hookrightarrow VG_{N'}^\bullet$ and apply the above theorem to show the symmetric monoidal structure on
$VG_N^\bullet \hookrightarrow VG_{N'}^\bullet$ and apply the above theorem to show the symmetric monoidal structure on ![]() $\mathrm {Loc}(VG;\mathrm {Sp})$. The module structure on
$\mathrm {Loc}(VG;\mathrm {Sp})$. The module structure on ![]() $\mathrm {Loc}(\widehat {Q})$ can be obtained appealing to a similar theorem as above for modules. We make a couple of remarks. First, one can also construct a simplicial object
$\mathrm {Loc}(\widehat {Q})$ can be obtained appealing to a similar theorem as above for modules. We make a couple of remarks. First, one can also construct a simplicial object ![]() $VG_N^\bullet$ that represents an associative algebra object in
$VG_N^\bullet$ that represents an associative algebra object in ![]() $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$, but it is not a Segal object (it is not even a Segal object in
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$, but it is not a Segal object (it is not even a Segal object in ![]() $\mathcal {S}\mathrm {pc}$), so the above theorem strictly generalizes the construction from Segal objects in [Reference Gaitsgory and RozenblyumGR17]. Second, the vertical map
$\mathcal {S}\mathrm {pc}$), so the above theorem strictly generalizes the construction from Segal objects in [Reference Gaitsgory and RozenblyumGR17]. Second, the vertical map ![]() $a_{N,M}$ of the right correspondence in (1.8.1) is not proper, so one cannot regard the correspondence as in
$a_{N,M}$ of the right correspondence in (1.8.1) is not proper, so one cannot regard the correspondence as in ![]() $\mathcal {S}\mathrm {pc}$.
$\mathcal {S}\mathrm {pc}$.
1.9 Related results and future work
Claim 1 in [Reference Jin and TreumannJT24] was motivated by the Nadler–Zaslow theorem (see [Reference Nadler and ZaslowNZ09, Reference NadlerNad09]) and the notion of brane structures on an exact Lagrangian submanifold ![]() $L\subset T^*X$ in Floer theory (cf. [Reference SeidelSei08]), whose obstruction classes are given by the Maslov class in
$L\subset T^*X$ in Floer theory (cf. [Reference SeidelSei08]), whose obstruction classes are given by the Maslov class in ![]() $H^1(L,\mathbf {Z})$ and the second (relative) Stiefel–Whitney class in
$H^1(L,\mathbf {Z})$ and the second (relative) Stiefel–Whitney class in ![]() $H^2(L;\mathbf {Z}/2\mathbf {Z})$. The obstruction classes are exactly the obstruction to the triviality of the composite map
$H^2(L;\mathbf {Z}/2\mathbf {Z})$. The obstruction classes are exactly the obstruction to the triviality of the composite map
where ![]() $\varphi _{\mathbf {Z}}$ is induced from the canonical commutative ring spectrum homomorphism
$\varphi _{\mathbf {Z}}$ is induced from the canonical commutative ring spectrum homomorphism ![]() $\mathbf {S}\rightarrow \mathbf {Z}$.
$\mathbf {S}\rightarrow \mathbf {Z}$.
For ![]() $L$ a compact exact Lagrangian submanifold in the cotangent bundle of a compact manifold, it is a prediction from Arnold's nearby Lagrangian conjecture that the classifying map
$L$ a compact exact Lagrangian submanifold in the cotangent bundle of a compact manifold, it is a prediction from Arnold's nearby Lagrangian conjecture that the classifying map ![]() $L\rightarrow B\mathrm {Pic}(\mathbf {S})$ is trivial. This is confirmed in [Reference Abouzaid and KraghAK16] whose approach is based on Floer (homotopy) theory (cf. [Reference Cohen, Jones and SegalCJS95]). Using sheaf quantization over
$L\rightarrow B\mathrm {Pic}(\mathbf {S})$ is trivial. This is confirmed in [Reference Abouzaid and KraghAK16] whose approach is based on Floer (homotopy) theory (cf. [Reference Cohen, Jones and SegalCJS95]). Using sheaf quantization over ![]() $\mathbf {Z}$, it is proved in [Reference GuillermouGui23] that this is the case when
$\mathbf {Z}$, it is proved in [Reference GuillermouGui23] that this is the case when ![]() $\mathbf {S}$ is replaced by
$\mathbf {S}$ is replaced by ![]() $\mathbf {Z}$. The sheaf of brane structures in our setting is called the Kashiwara–Schapira stack there. In the subsequent work [Reference JinJin20], we prove the triviality of the classifying map using microlocal sheaf theory over
$\mathbf {Z}$. The sheaf of brane structures in our setting is called the Kashiwara–Schapira stack there. In the subsequent work [Reference JinJin20], we prove the triviality of the classifying map using microlocal sheaf theory over ![]() $\mathbf {S}$.
$\mathbf {S}$.
The ![]() $E_\infty$-structure of
$E_\infty$-structure of ![]() $BJ$ in Claim 1.1 is used when the Gauss map
$BJ$ in Claim 1.1 is used when the Gauss map ![]() $\gamma$ has an
$\gamma$ has an ![]() $E_\infty$-structure or more generally
$E_\infty$-structure or more generally ![]() $E_n$-structure. An example that is crucial to the sheaf-theoretic approach to symplectic topology is the
$E_n$-structure. An example that is crucial to the sheaf-theoretic approach to symplectic topology is the ![]() $E_\infty$-map
$E_\infty$-map ![]() $U\rightarrow U/O$ that comes from taking stabilization of the linear symplectic group actions on
$U\rightarrow U/O$ that comes from taking stabilization of the linear symplectic group actions on ![]() $T^*\mathbf {R}^N$. In [Reference LurieLur15], it is conjectured that the obstruction to define a Fukaya category over
$T^*\mathbf {R}^N$. In [Reference LurieLur15], it is conjectured that the obstruction to define a Fukaya category over ![]() $\mathbf {S}$ on a symplectic
$\mathbf {S}$ on a symplectic ![]() $2n$-manifold
$2n$-manifold ![]() $M$ is the composition
$M$ is the composition
where the first map is the stabilization of the classifying map for the tangent bundle as an ![]() $U(n)$-bundle, and
$U(n)$-bundle, and ![]() $J_{\mathbf {C}}: \mathbf {Z}\times BU\rightarrow \mathrm {Pic}(\mathbf {S})$ is the complex
$J_{\mathbf {C}}: \mathbf {Z}\times BU\rightarrow \mathrm {Pic}(\mathbf {S})$ is the complex ![]() $J$-homomorphism. By the compatibility of the complex
$J$-homomorphism. By the compatibility of the complex ![]() $J$-homomorphism with the real
$J$-homomorphism with the real ![]() $J$-homomorphism, one has
$J$-homomorphism, one has ![]() $B^2J_{\mathbf {C}}$ is homotopic to the delooping of the classifying map of brane structures
$B^2J_{\mathbf {C}}$ is homotopic to the delooping of the classifying map of brane structures ![]() $U\rightarrow U/O\rightarrow B\mathrm {Pic}(\mathbf {S})$.
$U\rightarrow U/O\rightarrow B\mathrm {Pic}(\mathbf {S})$.
The analogue of the Fukaya category in sheaf theory for a Weinstein manifold ![]() $M$ with a choice of Lagrangian skeleton
$M$ with a choice of Lagrangian skeleton ![]() $\Lambda$ is the microlocal sheaf category along
$\Lambda$ is the microlocal sheaf category along ![]() $\Lambda$. We will show in a future work that the obstruction to defining a microlocal sheaf category along
$\Lambda$. We will show in a future work that the obstruction to defining a microlocal sheaf category along ![]() $\Lambda$ is exactly the obstruction given by (1.9.1) and this is based on the
$\Lambda$ is exactly the obstruction given by (1.9.1) and this is based on the ![]() $E_1$-structure on the classifying map
$E_1$-structure on the classifying map ![]() $U\rightarrow B\mathrm {Pic}(\mathbf {S})$. There is a different approach to this using
$U\rightarrow B\mathrm {Pic}(\mathbf {S})$. There is a different approach to this using ![]() $h$-principle given in [Reference ShendeShe21, Reference Nadler and ShendeNS20].
$h$-principle given in [Reference ShendeShe21, Reference Nadler and ShendeNS20].
2. Background and results on the  $(\infty,2)$-categories of correspondences
$(\infty,2)$-categories of correspondences
We recall the definition of the ![]() $(\infty,2)$-categories of correspondences for an
$(\infty,2)$-categories of correspondences for an ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$ and its (symmetric) monoidal structure when
$\mathcal {C}$ and its (symmetric) monoidal structure when ![]() $\mathcal {C}$ is (symmetric) monoidal. Then we present several concrete constructions of (commutative) algebra objects, their modules and (right-lax) homomorphisms when
$\mathcal {C}$ is (symmetric) monoidal. Then we present several concrete constructions of (commutative) algebra objects, their modules and (right-lax) homomorphisms when ![]() $\mathcal {C}$ has the Cartesian symmetric monoidal structure.
$\mathcal {C}$ has the Cartesian symmetric monoidal structure.
2.1 The definition of the  $(\infty,2)$-categories of correspondences
$(\infty,2)$-categories of correspondences
The materials in this subsection are following [Reference Gaitsgory and RozenblyumGR17, Chapters A.1 and V.1]. Let ![]() $1\text {-}\mathcal {C}\mathrm {at}$ denote the
$1\text {-}\mathcal {C}\mathrm {at}$ denote the ![]() $(\infty,1)$-category of (small)
$(\infty,1)$-category of (small) ![]() $(\infty, 1)$-categories. Let
$(\infty, 1)$-categories. Let ![]() $2\text {-}\mathcal {C}\mathrm {at}$ be the
$2\text {-}\mathcal {C}\mathrm {at}$ be the ![]() $(\infty,1)$-category of
$(\infty,1)$-category of ![]() $(\infty,2)$-categories, defined as the full subcategory of complete Segal objects in
$(\infty,2)$-categories, defined as the full subcategory of complete Segal objects in ![]() $(1\text {-}\mathcal {C}\mathrm {at})^{\Delta ^{\rm op}}$. The tautological full embedding is denoted by
$(1\text {-}\mathcal {C}\mathrm {at})^{\Delta ^{\rm op}}$. The tautological full embedding is denoted by
We use the convention that a category in bold face means an ![]() $(\infty,2)$-category. For example,
$(\infty,2)$-category. For example, ![]() $\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}}$ means the
$\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}}$ means the ![]() $(\infty,2)$-category of presentable stable
$(\infty,2)$-category of presentable stable ![]() $\infty$-categories with 2-morphisms given by natural transformations.
$\infty$-categories with 2-morphisms given by natural transformations.
Let ![]() $\mathcal {C}$ be an
$\mathcal {C}$ be an ![]() $(\infty,1)$-category which admits finite limits. Let
$(\infty,1)$-category which admits finite limits. Let ![]() $([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}$ be the full subcategory of
$([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}$ be the full subcategory of ![]() $[n]\times [n]^{\rm op}$, consisting of objects
$[n]\times [n]^{\rm op}$, consisting of objects ![]() $(i,j), j\geq i$, pictorially given by
$(i,j), j\geq i$, pictorially given by

Let ![]() $'\mathrm {Grid}_n^{\geq \mathrm {dgnl}}(\mathcal {C})$ be the 1-full subcategory of
$'\mathrm {Grid}_n^{\geq \mathrm {dgnl}}(\mathcal {C})$ be the 1-full subcategory of ![]() $\mathrm {Fun}(([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}},\mathcal {C})$ whose objects, viewed as diagrams in
$\mathrm {Fun}(([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}},\mathcal {C})$ whose objects, viewed as diagrams in ![]() $\mathcal {C}$, have each square a Cartesian square in
$\mathcal {C}$, have each square a Cartesian square in ![]() $\mathcal {C}$, and whose morphisms
$\mathcal {C}$, and whose morphisms ![]() $\eta : F_1\rightarrow F_2$ satisfy that the induced morphisms
$\eta : F_1\rightarrow F_2$ satisfy that the induced morphisms ![]() $F_1(i,i)\rightarrow F_2(i,i)$ are isomorphisms for
$F_1(i,i)\rightarrow F_2(i,i)$ are isomorphisms for ![]() $0\leq i\leq n$. Let
$0\leq i\leq n$. Let ![]() $''\mathrm {Grid}_n^{\geq \mathrm {dgnl}}(\mathcal {C})$ be the maximal Kan subcomplex of
$''\mathrm {Grid}_n^{\geq \mathrm {dgnl}}(\mathcal {C})$ be the maximal Kan subcomplex of ![]() $'\mathrm {Grid}_n^{\geq \mathrm {dgnl}}(\mathcal {C})$, i.e. the 1-morphisms
$'\mathrm {Grid}_n^{\geq \mathrm {dgnl}}(\mathcal {C})$, i.e. the 1-morphisms ![]() $\eta : F_1\rightarrow F_2$ in
$\eta : F_1\rightarrow F_2$ in ![]() $''\mathrm {Grid}_n^{\geq \mathrm {dgnl}}(\mathcal {C})$ further satisfy that the morphism at each entry
$''\mathrm {Grid}_n^{\geq \mathrm {dgnl}}(\mathcal {C})$ further satisfy that the morphism at each entry ![]() $F_1(i,j)\rightarrow F_2(i,j)$ is an isomorphism for all
$F_1(i,j)\rightarrow F_2(i,j)$ is an isomorphism for all ![]() $0\leq i\leq j\leq n$.
$0\leq i\leq j\leq n$.
Define ![]() $\mathbf {Corr}(\mathcal {C})$ to be the
$\mathbf {Corr}(\mathcal {C})$ to be the ![]() $(\infty,2)$-category, considered as an object in
$(\infty,2)$-category, considered as an object in ![]() $(1\text {-}\mathcal {C}\mathrm {at})^{\Delta ^{\rm op}}$, given by
$(1\text {-}\mathcal {C}\mathrm {at})^{\Delta ^{\rm op}}$, given by
Let ![]() $\mathrm {Corr}(\mathcal {C})$ be the
$\mathrm {Corr}(\mathcal {C})$ be the ![]() $(\infty,1)$-category given by
$(\infty,1)$-category given by
More generally, if we fix three classes of morphisms in ![]() $\mathcal {C}$ denoted by
$\mathcal {C}$ denoted by ![]() $vert,horiz,adm$ satisfying some natural conditions (see [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 1.1.1] for the precise conditions), then we can define
$vert,horiz,adm$ satisfying some natural conditions (see [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 1.1.1] for the precise conditions), then we can define ![]() $\mathrm {Corr}(\mathcal {C})_{vert,horiz}^{adm}$ to be the 2-full subcategory of
$\mathrm {Corr}(\mathcal {C})_{vert,horiz}^{adm}$ to be the 2-full subcategory of ![]() $\mathbf {Corr}(\mathcal {C})$ with the vertical (respectively, horizontal) arrow in a 1-morphism belonging to
$\mathbf {Corr}(\mathcal {C})$ with the vertical (respectively, horizontal) arrow in a 1-morphism belonging to ![]() $vert$ (respectively,
$vert$ (respectively, ![]() $horiz$), and the 2-morphisms lying in
$horiz$), and the 2-morphisms lying in ![]() $adm$. If
$adm$. If ![]() $adm=\mathsf {isom}$, where
$adm=\mathsf {isom}$, where ![]() $\mathsf {isom}$ is the class of isomorphisms, then we will also denote
$\mathsf {isom}$ is the class of isomorphisms, then we will also denote ![]() $\mathrm {Corr}(\mathcal {C})_{vert, horiz}^{\mathsf {isom}}$ by
$\mathrm {Corr}(\mathcal {C})_{vert, horiz}^{\mathsf {isom}}$ by ![]() $\mathrm {Corr}(\mathcal {C})_{vert,horiz}$.
$\mathrm {Corr}(\mathcal {C})_{vert,horiz}$.
2.2 (Symmetric) monoidal structure on  $\mathbf {Corr}(\mathcal {C})$
$\mathbf {Corr}(\mathcal {C})$
Following [Reference Gaitsgory and RozenblyumGR17, Chapter 9, 4.8.1], one can give a description of a 2-coCartesian fibrationFootnote 6 ![]() $\mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}\rightarrow N(\Delta )^{\rm op}$ (respectively,
$\mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}\rightarrow N(\Delta )^{\rm op}$ (respectively, ![]() $\mathbf {Corr}(\mathcal {C})^{\otimes, \mathrm {Fin}_*}\rightarrow N(\mathrm {Fin}_*)$) for the (symmetric) monoidal structure on
$\mathbf {Corr}(\mathcal {C})^{\otimes, \mathrm {Fin}_*}\rightarrow N(\mathrm {Fin}_*)$) for the (symmetric) monoidal structure on ![]() $\mathbf {Corr}(\mathcal {C})$ inherited from a (symmetric) monoidal structure
$\mathbf {Corr}(\mathcal {C})$ inherited from a (symmetric) monoidal structure ![]() $\mathcal {C}^{\otimes }$ as follows (See [Reference Liu and ZhengLZ12] for a similar construction in the
$\mathcal {C}^{\otimes }$ as follows (See [Reference Liu and ZhengLZ12] for a similar construction in the ![]() $(\infty,1)$-categorical setting). By the straightening theorem for
$(\infty,1)$-categorical setting). By the straightening theorem for ![]() $(\infty, 2)$-categories [Reference Gaitsgory and RozenblyumGR17, Chapter 11, Theorem 1.1.8, Corollary 1.3.3], 2-coCartesian fibrations over an
$(\infty, 2)$-categories [Reference Gaitsgory and RozenblyumGR17, Chapter 11, Theorem 1.1.8, Corollary 1.3.3], 2-coCartesian fibrations over an ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\mathbb {D}$ are equivalent to functors from
$\mathbb {D}$ are equivalent to functors from ![]() $\mathbb {D}$ to the
$\mathbb {D}$ to the ![]() $(\infty,2)$-category of
$(\infty,2)$-category of ![]() $(\infty,2)$-categories.
$(\infty,2)$-categories.
Let ![]() $p: \mathcal {C}^{\otimes,\Delta }\rightarrow N(\Delta )$ (respectively,
$p: \mathcal {C}^{\otimes,\Delta }\rightarrow N(\Delta )$ (respectively, ![]() $p: \mathcal {C}^{\otimes,(\mathrm {Fin}_*)^{\rm op}}\rightarrow N(\mathrm {Fin}_*)^{\rm op}$ be the Cartesian fibration associated to the (symmetric) monoidal structure
$p: \mathcal {C}^{\otimes,(\mathrm {Fin}_*)^{\rm op}}\rightarrow N(\mathrm {Fin}_*)^{\rm op}$ be the Cartesian fibration associated to the (symmetric) monoidal structure ![]() $\mathcal {C}^{\otimes }$. Then we have
$\mathcal {C}^{\otimes }$. Then we have
 \begin{equation} \begin{aligned} & \mathrm{Seq}_k(\mathbf{Corr}(\mathcal{C})^{\otimes,\Delta^{\rm op}}):=\mathrm{Fun}''(([k]\times[k]^{\rm op})^{\geq \mathrm{dgnl}}, \mathcal{C}^{\otimes, \Delta})\\ & \mathrm{Seq}_k(\mathbf{Corr}(\mathcal{C})^{\otimes,\mathrm{Fin}_*}):=\mathrm{Fun}''(([k]\times[k]^{\rm op})^{\geq \mathrm{dgnl}}, \mathcal{C}^{\otimes, (\mathrm{Fin}_*)^{\rm op}}), \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & \mathrm{Seq}_k(\mathbf{Corr}(\mathcal{C})^{\otimes,\Delta^{\rm op}}):=\mathrm{Fun}''(([k]\times[k]^{\rm op})^{\geq \mathrm{dgnl}}, \mathcal{C}^{\otimes, \Delta})\\ & \mathrm{Seq}_k(\mathbf{Corr}(\mathcal{C})^{\otimes,\mathrm{Fin}_*}):=\mathrm{Fun}''(([k]\times[k]^{\rm op})^{\geq \mathrm{dgnl}}, \mathcal{C}^{\otimes, (\mathrm{Fin}_*)^{\rm op}}), \end{aligned} \end{equation}
where ![]() $\mathrm {Fun}''(([k]\times [k]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\otimes, \Delta })$ is defined as follows. First, let
$\mathrm {Fun}''(([k]\times [k]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\otimes, \Delta })$ is defined as follows. First, let ![]() $\mathrm {Maps}'(([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}, N(\Delta ))$ be the full subcategory of
$\mathrm {Maps}'(([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}, N(\Delta ))$ be the full subcategory of ![]() $\mathrm {Maps}(([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}, N(\Delta ))$ consisting of functors that map vertical arrows in
$\mathrm {Maps}(([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}, N(\Delta ))$ consisting of functors that map vertical arrows in ![]() $([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}$ to identity morphisms (more precisely, the contractible component of each self-morphism space containing the identity morphism) in
$([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}$ to identity morphisms (more precisely, the contractible component of each self-morphism space containing the identity morphism) in ![]() $N(\Delta )$, and we have
$N(\Delta )$, and we have ![]() $\mathrm {Fun}'(([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\otimes,\Delta })$ defined as the following pullback.
$\mathrm {Fun}'(([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\otimes,\Delta })$ defined as the following pullback.

Then ![]() $\mathrm {Fun}''(([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\otimes, \Delta })$ is the 1-full subcategory of
$\mathrm {Fun}''(([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\otimes, \Delta })$ is the 1-full subcategory of ![]() $\mathrm {Fun}'([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\otimes,\Delta })$ whose objects
$\mathrm {Fun}'([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\otimes,\Delta })$ whose objects ![]() $F$ and morphisms
$F$ and morphisms ![]() $q: F\rightarrow F'$ are those satisfying (Obj) and (Mor) below, respectively.
$q: F\rightarrow F'$ are those satisfying (Obj) and (Mor) below, respectively.
(Obj) For every square
 $\Delta ^{1}_{vert}\times \Delta ^{1}_{hor}$ in
$\Delta ^{1}_{vert}\times \Delta ^{1}_{hor}$ in  $([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}$, its image under
$([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}$, its image under  $F$ is an edge
$F$ is an edge  $(f: x\rightarrow y)\in \mathrm {Fun}(\Delta _{vert}^1,\mathcal {C}^{\otimes, \Delta })$, where
$(f: x\rightarrow y)\in \mathrm {Fun}(\Delta _{vert}^1,\mathcal {C}^{\otimes, \Delta })$, where  $p(x)=id_{[k]}, p(y)=id_{[m]}$. Let
$p(x)=id_{[k]}, p(y)=id_{[m]}$. Let  $h$ be a Cartesian edge ending at
$h$ be a Cartesian edge ending at  $y$ of the Cartesian fibration
$y$ of the Cartesian fibration  $\widetilde {p}:\mathrm {Fun}(\Delta ^1_{vert}, \mathcal {C}^{\otimes, \Delta })\rightarrow \mathrm {Fun}(\Delta ^1_{vert}, N(\Delta ))$ over
$\widetilde {p}:\mathrm {Fun}(\Delta ^1_{vert}, \mathcal {C}^{\otimes, \Delta })\rightarrow \mathrm {Fun}(\Delta ^1_{vert}, N(\Delta ))$ over  $\widetilde {p}(f)$. Then there exists a (contractible space of) morphism(s)
$\widetilde {p}(f)$. Then there exists a (contractible space of) morphism(s)  $g$ in
$g$ in  $\mathrm {Fun}(\Delta ^1_{vert}, \mathcal {C}^{\otimes, \Delta })$ together with a homotopy
$\mathrm {Fun}(\Delta ^1_{vert}, \mathcal {C}^{\otimes, \Delta })$ together with a homotopy  $f\simeq h\circ g$. We require that the square in
$f\simeq h\circ g$. We require that the square in  $\mathcal {C}^{\otimes, \Delta }_{[k]}\simeq (\mathcal {C})^{\times k}$ determined by
$\mathcal {C}^{\otimes, \Delta }_{[k]}\simeq (\mathcal {C})^{\times k}$ determined by  $g$ is a Cartesian square.
$g$ is a Cartesian square.(Mor) We have that
 $q((i,i)): F((i,i))\rightarrow F'((i,i))$ is an isomorphism for all
$q((i,i)): F((i,i))\rightarrow F'((i,i))$ is an isomorphism for all  $0\leq i\leq k$.
$0\leq i\leq k$.
The ![]() $\infty$-category
$\infty$-category ![]() $\mathrm {Fun}''(([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\otimes, (\mathrm {Fin}_*)^{\rm op}})$ is defined in the same way. We first prove that the natural functor
$\mathrm {Fun}''(([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\otimes, (\mathrm {Fin}_*)^{\rm op}})$ is defined in the same way. We first prove that the natural functor ![]() $p_{\mathbf {Corr}(\mathcal {C})}: \mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}\rightarrow N(\Delta )^{\rm op}$ (respectively,
$p_{\mathbf {Corr}(\mathcal {C})}: \mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}\rightarrow N(\Delta )^{\rm op}$ (respectively, ![]() $p_{\mathbf {Corr}(\mathcal {C})}^{\mathrm {Comm}}: \mathbf {Corr}(\mathcal {C})^{\otimes, \mathrm {Fin}_*}\rightarrow N(\mathrm {Fin}_*)$) represents a monoidal (respectively, symmetric monoidal) structure on
$p_{\mathbf {Corr}(\mathcal {C})}^{\mathrm {Comm}}: \mathbf {Corr}(\mathcal {C})^{\otimes, \mathrm {Fin}_*}\rightarrow N(\mathrm {Fin}_*)$) represents a monoidal (respectively, symmetric monoidal) structure on ![]() $\mathbf {Corr}(\mathcal {C})$.
$\mathbf {Corr}(\mathcal {C})$.
Proposition 2.1 The functor ![]() $p_{\mathbf {Corr}(\mathcal {C})}: \mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}\rightarrow N(\Delta )^{\rm op}$ (respectively,
$p_{\mathbf {Corr}(\mathcal {C})}: \mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}\rightarrow N(\Delta )^{\rm op}$ (respectively, ![]() $p_{\mathbf {Corr}(\mathcal {C})}^{\mathrm {Comm}}: \mathbf {Corr}(\mathcal {C})^{\otimes, \mathrm {Fin}_*}\rightarrow N(\mathrm {Fin}_*)$) is a 2-coCartesian fibration in the sense of [Reference Gaitsgory and RozenblyumGR17, Chapter 11, Definition 1.1.2].
$p_{\mathbf {Corr}(\mathcal {C})}^{\mathrm {Comm}}: \mathbf {Corr}(\mathcal {C})^{\otimes, \mathrm {Fin}_*}\rightarrow N(\mathrm {Fin}_*)$) is a 2-coCartesian fibration in the sense of [Reference Gaitsgory and RozenblyumGR17, Chapter 11, Definition 1.1.2].
First let us state the definition of a 2-coCartesian fibration (see [Reference Gaitsgory and RozenblyumGR17, Chapter 11, Definition 1.1.2, § 1.3.1]).
Definition 2.2 Let ![]() $F: \mathcal {D}\rightarrow \mathcal {E}$ be a functor of
$F: \mathcal {D}\rightarrow \mathcal {E}$ be a functor of ![]() $(\infty,2)$-categories. We say
$(\infty,2)$-categories. We say ![]() $f: x\rightarrow y$, a
$f: x\rightarrow y$, a ![]() $1$-morphism in
$1$-morphism in ![]() $\mathcal {D}$, is a 2-coCartesian morphism with respect to
$\mathcal {D}$, is a 2-coCartesian morphism with respect to ![]() $F$ if the induced functor
$F$ if the induced functor
is an equivalence of ![]() $\infty$-categories for every
$\infty$-categories for every ![]() $z\in \mathcal {D}$.
$z\in \mathcal {D}$.
Definition 2.3 Let ![]() $F: \mathcal {D}\rightarrow \mathcal {E}$ be a functor of
$F: \mathcal {D}\rightarrow \mathcal {E}$ be a functor of ![]() $(\infty,2)$-categories. We say
$(\infty,2)$-categories. We say ![]() $F$ is a 2-coCartesian fibration if:
$F$ is a 2-coCartesian fibration if:
(i) for any morphism
 $f: s\rightarrow t$ in
$f: s\rightarrow t$ in  $\mathcal {E}$ and any object
$\mathcal {E}$ and any object  $x$ in
$x$ in  $\mathcal {D}$ over
$\mathcal {D}$ over  $s$, there exists a 2-coCartesian 1-morphism in
$s$, there exists a 2-coCartesian 1-morphism in  $\mathcal {D}$ emitting from
$\mathcal {D}$ emitting from  $x$ that covers
$x$ that covers  $f$;
$f$;(iia) for every object
 $x,y$ in
$x,y$ in  $\mathcal {D}$, one has
$\mathcal {D}$, one has  ${\mathcal{M}\text{aps}}_{\mathcal {D}}(x,y)\rightarrow {\mathcal {M} \text{aps}}_{\mathcal {E}}(F(x), F(y))$ a Cartesian fibration;
${\mathcal{M}\text{aps}}_{\mathcal {D}}(x,y)\rightarrow {\mathcal {M} \text{aps}}_{\mathcal {E}}(F(x), F(y))$ a Cartesian fibration;(iib) for any
 $1$-morphisms
$1$-morphisms  $f: x\rightarrow y$ and
$f: x\rightarrow y$ and  $g: z\rightarrow w$, the induced functors
send each Cartesian morphism over
$g: z\rightarrow w$, the induced functors
send each Cartesian morphism over \[ {\mathcal{M}\text{aps}}_{\mathcal{D}}(y,z)\rightarrow {\mathcal{M}\text{aps}}_{\mathcal{D}}(x,z), \ {\mathcal{M}\text{aps}}_{\mathcal{D}}(y,z)\rightarrow {\mathcal{M}\text{aps}}_{\mathcal{D}}(y,w) \]
\[ {\mathcal{M}\text{aps}}_{\mathcal{D}}(y,z)\rightarrow {\mathcal{M}\text{aps}}_{\mathcal{D}}(x,z), \ {\mathcal{M}\text{aps}}_{\mathcal{D}}(y,z)\rightarrow {\mathcal{M}\text{aps}}_{\mathcal{D}}(y,w) \]
 ${\mathcal {M} \text{aps}}_{\mathcal {E}}(F(y), F(z))$ to a Cartesian morphism over
${\mathcal {M} \text{aps}}_{\mathcal {E}}(F(y), F(z))$ to a Cartesian morphism over  ${\mathcal {M} \text{aps}}_{\mathcal {E}}(F(x),F(z))$ and
${\mathcal {M} \text{aps}}_{\mathcal {E}}(F(x),F(z))$ and  ${\mathcal {M} \text{aps}}_{\mathcal {E}}(F(y),F(w))$, respectively.
${\mathcal {M} \text{aps}}_{\mathcal {E}}(F(y),F(w))$, respectively.
Proof of Proposition 2.1 We claim that a 1-morphism in ![]() $\mathbf {Corr}(\mathcal {C})^{\otimes,\Delta ^{\rm op}}$ represented by any element in
$\mathbf {Corr}(\mathcal {C})^{\otimes,\Delta ^{\rm op}}$ represented by any element in ![]() $f\in \mathrm {Fun}''(([1]\times [1]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\otimes,\Delta })$ is 2-coCartesian if both its horizontal and vertical arrows go to Cartesian arrows in
$f\in \mathrm {Fun}''(([1]\times [1]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\otimes,\Delta })$ is 2-coCartesian if both its horizontal and vertical arrows go to Cartesian arrows in ![]() $\mathcal {C}^{\otimes, \Delta }$. Once this is proved, part (i) becomes an immediate consequence. To see the claim, for any
$\mathcal {C}^{\otimes, \Delta }$. Once this is proved, part (i) becomes an immediate consequence. To see the claim, for any ![]() $f:x\rightarrow y$ and
$f:x\rightarrow y$ and ![]() $z$ in
$z$ in ![]() $\mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}$ over
$\mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}$ over ![]() $p_{\mathbf {Corr}(\mathcal {C})}(f)^{\rm op}:[m]\rightarrow [\ell ]$ and
$p_{\mathbf {Corr}(\mathcal {C})}(f)^{\rm op}:[m]\rightarrow [\ell ]$ and ![]() $[n]$, respectively,
$[n]$, respectively,

where the vertical arrow in the diagram representing ![]() $f$ is an isomorphism, we have
$f$ is an isomorphism, we have
and the right-hand side of (2.2.3) equivalent to
The functor (2.2.3) is homotopic to the composition
 \begin{align*} &(\mathcal{C}^{\otimes, \Delta}_{[n]})_{/z}\times_{\mathcal{C}^{\otimes,\Delta}} \mathcal{C}^{\otimes, \Delta}_{/y}\overset{\sim}{\rightarrow} (\mathcal{C}^{\otimes, \Delta}_{[n]})_{/z}\times_{\mathcal{C}^{\otimes,\Delta}} \mathcal{C}^{\otimes, \Delta}_{/f_{hor}}\\ &\rightarrow (\mathcal{C}^{\otimes, \Delta}_{[n]})_{/z}\times_{\mathcal{C}^{\otimes,\Delta}} (\mathcal{C}^{\otimes, \Delta}_{/x}\times_{N(\Delta)_{/[\ell]}} N(\Delta)_{/p_{\mathbf{Corr}(\mathcal{C})}(f)^{\rm op}}), \end{align*}
\begin{align*} &(\mathcal{C}^{\otimes, \Delta}_{[n]})_{/z}\times_{\mathcal{C}^{\otimes,\Delta}} \mathcal{C}^{\otimes, \Delta}_{/y}\overset{\sim}{\rightarrow} (\mathcal{C}^{\otimes, \Delta}_{[n]})_{/z}\times_{\mathcal{C}^{\otimes,\Delta}} \mathcal{C}^{\otimes, \Delta}_{/f_{hor}}\\ &\rightarrow (\mathcal{C}^{\otimes, \Delta}_{[n]})_{/z}\times_{\mathcal{C}^{\otimes,\Delta}} (\mathcal{C}^{\otimes, \Delta}_{/x}\times_{N(\Delta)_{/[\ell]}} N(\Delta)_{/p_{\mathbf{Corr}(\mathcal{C})}(f)^{\rm op}}), \end{align*}
where ![]() $f_{hor}$ is the horizontal arrow that represents
$f_{hor}$ is the horizontal arrow that represents ![]() $f$. Now the horizontal arrow in the graph representing
$f$. Now the horizontal arrow in the graph representing ![]() $f$ is Cartesian in
$f$ is Cartesian in ![]() $\mathcal {C}^{\otimes, \Delta }$ means that
$\mathcal {C}^{\otimes, \Delta }$ means that
which implies that ![]() $f$ is a 2-coCartesian morphism.
$f$ is a 2-coCartesian morphism.
It is clear that ![]() $p_{\mathbf {Corr}(\mathcal {C})}$ satisfies parts (iia) and (iib), since the mapping space of any two objects in
$p_{\mathbf {Corr}(\mathcal {C})}$ satisfies parts (iia) and (iib), since the mapping space of any two objects in ![]() $N(\Delta )$ is discrete and then a Cartesian morphism in
$N(\Delta )$ is discrete and then a Cartesian morphism in ![]() ${\mathcal {M} \text{aps}}_{\mathbf {Corr}(\mathcal {C})}(y,z)$ over
${\mathcal {M} \text{aps}}_{\mathbf {Corr}(\mathcal {C})}(y,z)$ over ![]() ${\mathcal {M} \text{aps}}_{N(\Delta )^{\rm op}}(F(y), F(z))$ is the same as an isomorphism.
${\mathcal {M} \text{aps}}_{N(\Delta )^{\rm op}}(F(y), F(z))$ is the same as an isomorphism.
A similar proof works for ![]() $p_{\mathbf {Corr}(\mathcal {C})}^{\mathrm {Comm}}: \mathbf {Corr}(\mathcal {C})^{\otimes, \mathrm {Fin}_*}\rightarrow N(\mathrm {Fin}_*)$.
$p_{\mathbf {Corr}(\mathcal {C})}^{\mathrm {Comm}}: \mathbf {Corr}(\mathcal {C})^{\otimes, \mathrm {Fin}_*}\rightarrow N(\mathrm {Fin}_*)$.
Proposition 2.4 The 2-coCartesian fibration ![]() $p_{\mathbf {Corr}(\mathcal {C})}: \mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}\rightarrow N(\Delta )^{\rm op}$ (respectively,
$p_{\mathbf {Corr}(\mathcal {C})}: \mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}\rightarrow N(\Delta )^{\rm op}$ (respectively, ![]() $p_{\mathbf {Corr}(\mathcal {C})}^{\mathrm {Comm}}: \mathbf {Corr}(\mathcal {C})^{\otimes, \mathrm {Fin}_*}\rightarrow N(\mathrm {Fin}_*)$) represents a monoidal (respectively, symmetric monoidal) structure on
$p_{\mathbf {Corr}(\mathcal {C})}^{\mathrm {Comm}}: \mathbf {Corr}(\mathcal {C})^{\otimes, \mathrm {Fin}_*}\rightarrow N(\mathrm {Fin}_*)$) represents a monoidal (respectively, symmetric monoidal) structure on ![]() $\mathbf {Corr}(\mathcal {C})$.
$\mathbf {Corr}(\mathcal {C})$.
Proof. First, the fiber of ![]() $p_{\mathbf {Corr}(\mathcal {C})}$ at
$p_{\mathbf {Corr}(\mathcal {C})}$ at ![]() $[1]$, denoted as
$[1]$, denoted as ![]() $\mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}_{[1]}$, has
$\mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}_{[1]}$, has ![]() $\mathrm {Seq}_k(\mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}_{[1]})$ the full subcategory of
$\mathrm {Seq}_k(\mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}_{[1]})$ the full subcategory of ![]() $\mathrm {Fun}''(([k]\times [k]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\otimes,\Delta })$ consisting of objects whose image in
$\mathrm {Fun}''(([k]\times [k]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\otimes,\Delta })$ consisting of objects whose image in ![]() $\mathrm {Map}'(([k]\times [k]^{\rm op})^{\geq \mathrm {dgnl}}, N(\Delta ))$ are the constant functor to
$\mathrm {Map}'(([k]\times [k]^{\rm op})^{\geq \mathrm {dgnl}}, N(\Delta ))$ are the constant functor to ![]() $[1]\in N(\Delta )$. Therefore,
$[1]\in N(\Delta )$. Therefore, ![]() $\mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}_{[1]}$ is equivalent to
$\mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}_{[1]}$ is equivalent to ![]() $\mathbf {Corr}(\mathcal {C}^{\otimes,\Delta }_{[1]})\simeq \mathbf {Corr}(\mathcal {C})$.
$\mathbf {Corr}(\mathcal {C}^{\otimes,\Delta }_{[1]})\simeq \mathbf {Corr}(\mathcal {C})$.
Second, it is clear from unwinding the definitions that the natural functor induced from all the convex morphisms ![]() $[1]\rightarrow [n]$ in
$[1]\rightarrow [n]$ in ![]() $N(\Delta )$,
$N(\Delta )$,
is an equivalence for all ![]() $k>0$. It is also clear that the fiber
$k>0$. It is also clear that the fiber ![]() $\mathbf {Corr}(\mathcal {C})_{[0]}^{\otimes,\Delta ^{\rm op}}\simeq *$. Hence, the proposition follows.
$\mathbf {Corr}(\mathcal {C})_{[0]}^{\otimes,\Delta ^{\rm op}}\simeq *$. Hence, the proposition follows.
A similar argument works for ![]() $p_{\mathbf {Corr}(\mathcal {C})}^{\mathrm {Comm}}$.
$p_{\mathbf {Corr}(\mathcal {C})}^{\mathrm {Comm}}$.
2.2.1 A construction of Cartesian fibration  $\mathcal {C}^{\times,\Delta }\rightarrow N(\Delta )$ (respectively,
$\mathcal {C}^{\times,\Delta }\rightarrow N(\Delta )$ (respectively,  $\mathcal {C}^{\times,(\mathrm {Fin}_*)^{\rm op}}\rightarrow N(\mathrm {Fin}_*)^{\rm op}$) for a Cartesian monoidal structure
$\mathcal {C}^{\times,(\mathrm {Fin}_*)^{\rm op}}\rightarrow N(\mathrm {Fin}_*)^{\rm op}$) for a Cartesian monoidal structure
We give a model of ![]() $\mathcal {C}^{\times,\Delta }\rightarrow N(\Delta )$ representing a Cartesian monoidal structure on
$\mathcal {C}^{\times,\Delta }\rightarrow N(\Delta )$ representing a Cartesian monoidal structure on ![]() $\mathcal {C}$ that is a modification of that constructed in [Reference LurieLur07, Notation 1.2.7], which will later be convenient for us to construct algebra objects in
$\mathcal {C}$ that is a modification of that constructed in [Reference LurieLur07, Notation 1.2.7], which will later be convenient for us to construct algebra objects in ![]() $\mathrm {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}$ from a collection of concise and discrete data.
$\mathrm {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}$ from a collection of concise and discrete data.
We define ordinary 1-categories ![]() $T$ and
$T$ and ![]() $T^1$ over
$T^1$ over ![]() $N(\Delta )$ as follows. The category
$N(\Delta )$ as follows. The category ![]() $T^1$ consists of objects
$T^1$ consists of objects ![]() $([n], i\leq j)$ with any morphism
$([n], i\leq j)$ with any morphism ![]() $([n],i\leq j)\rightarrow ([m],i'\leq j')$ given by a morphism
$([n],i\leq j)\rightarrow ([m],i'\leq j')$ given by a morphism ![]() $f:[n]\rightarrow [m]$ in
$f:[n]\rightarrow [m]$ in ![]() $\Delta$ satisfying
$\Delta$ satisfying ![]() $[i',j']\subset [f(i), f(j)]$ (note the slight difference from
$[i',j']\subset [f(i), f(j)]$ (note the slight difference from ![]() $\Delta ^\times$ in [Reference LurieLur07, Notation 1.2.5]). Let
$\Delta ^\times$ in [Reference LurieLur07, Notation 1.2.5]). Let ![]() $T$ be the full subcategory of
$T$ be the full subcategory of ![]() $T^1$ consisting only of subintervals of length 1, i.e.
$T^1$ consisting only of subintervals of length 1, i.e. ![]() $([n], i\leq i+1)$. It is clear that
$([n], i\leq i+1)$. It is clear that ![]() $T^1\rightarrow N(\Delta )$ is a coCartesian fibration, with a morphism
$T^1\rightarrow N(\Delta )$ is a coCartesian fibration, with a morphism ![]() $f: ([n],i\leq j)\rightarrow ([m],i'\leq j')$ being coCartesian if and only if
$f: ([n],i\leq j)\rightarrow ([m],i'\leq j')$ being coCartesian if and only if ![]() $[i',j']=[f(i), f(j)]$. Under straightening, it corresponds to the functor that sends
$[i',j']=[f(i), f(j)]$. Under straightening, it corresponds to the functor that sends ![]() $[k]\in N(\Delta )$ to the poset of its nonempty convex subsets (with the opposite poset structure of inclusion).
$[k]\in N(\Delta )$ to the poset of its nonempty convex subsets (with the opposite poset structure of inclusion).
By the exactly same construction and argument as in [Reference LurieLur07, Notation 1.2.7, Proposition 1.2.8], for an ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$ admitting finite products, one can define
$\mathcal {C}$ admitting finite products, one can define ![]() $\widetilde {\mathcal {C}}^{\times, \Delta, 1}$ to be the simplicial set over
$\widetilde {\mathcal {C}}^{\times, \Delta, 1}$ to be the simplicial set over ![]() $N(\Delta )$ determined by the property that for any simplicial set
$N(\Delta )$ determined by the property that for any simplicial set ![]() $K$ over
$K$ over ![]() $N(\Delta )$
$N(\Delta )$
which is a Cartesian fibration over ![]() $N(\Delta )$, and define
$N(\Delta )$, and define ![]() $\mathcal {C}^{\times, \Delta, 1}$ to be the full subcategory of
$\mathcal {C}^{\times, \Delta, 1}$ to be the full subcategory of ![]() $\widetilde {\mathcal {C}}^{\times, \Delta, 1}$ consisting of
$\widetilde {\mathcal {C}}^{\times, \Delta, 1}$ consisting of ![]() $F\in \widetilde {\mathcal {C}}^{\times, \Delta, 1}_{[n]},[n]\in \Delta,$ such that the natural morphism
$F\in \widetilde {\mathcal {C}}^{\times, \Delta, 1}_{[n]},[n]\in \Delta,$ such that the natural morphism
is an isomorphism for all ![]() $0\leq i\leq j\leq n$, which is a Cartesian fibration over
$0\leq i\leq j\leq n$, which is a Cartesian fibration over ![]() $N(\Delta )$ as well. A morphism
$N(\Delta )$ as well. A morphism ![]() $p: F\rightarrow F'$ over
$p: F\rightarrow F'$ over ![]() $f: [n]\rightarrow [m]$ is a Cartesian morphism if and only if
$f: [n]\rightarrow [m]$ is a Cartesian morphism if and only if
is an isomorphism for all ![]() $0\leq i\leq j\leq n$.
$0\leq i\leq j\leq n$.
Now we define ![]() $\mathcal {C}^{\times,\Delta }$ over
$\mathcal {C}^{\times,\Delta }$ over ![]() $N(\Delta )$ as the simplicial set characterized by the property that for any simplicial set
$N(\Delta )$ as the simplicial set characterized by the property that for any simplicial set ![]() $K$ over
$K$ over ![]() $N(\Delta )$
$N(\Delta )$
Proposition 2.5 There is a natural equivalence ![]() $R:\mathcal {C}^{\times,\Delta,1}\rightarrow \mathcal {C}^{\times,\Delta }$ over
$R:\mathcal {C}^{\times,\Delta,1}\rightarrow \mathcal {C}^{\times,\Delta }$ over ![]() $N(\Delta )$, which is surjective on vertices of
$N(\Delta )$, which is surjective on vertices of ![]() $\mathcal {C}^{\times,\Delta }$. Thus,
$\mathcal {C}^{\times,\Delta }$. Thus, ![]() $\mathcal {C}^{\times, \Delta }$ is a Cartesian fibration over
$\mathcal {C}^{\times, \Delta }$ is a Cartesian fibration over ![]() $N(\Delta )$ and
$N(\Delta )$ and ![]() $p: F\rightarrow F'$ is a Cartesian morphism over
$p: F\rightarrow F'$ is a Cartesian morphism over ![]() $f:[n]\rightarrow [m]$ if and only if
$f:[n]\rightarrow [m]$ if and only if
is an isomorphism for all ![]() $0\leq i< n$.
$0\leq i< n$.
Proof. The functor ![]() $R$ is induced from the compatible system of restriction morphisms
$R$ is induced from the compatible system of restriction morphisms
for all ![]() $K$ over
$K$ over ![]() $N(\Delta )$. For each
$N(\Delta )$. For each ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {D}$ over
$\mathcal {D}$ over ![]() $N(\Delta )$, we have a map
$N(\Delta )$, we have a map
where ![]() $\mathrm {Maps}'(\mathcal {D}\times _{N(\Delta )}T^1,\mathcal {C})$ is the full subcategory of
$\mathrm {Maps}'(\mathcal {D}\times _{N(\Delta )}T^1,\mathcal {C})$ is the full subcategory of ![]() $\mathrm {Maps}(\mathcal {D}\times _{N(\Delta )}T^1,\mathcal {C})$ spanned by the functors
$\mathrm {Maps}(\mathcal {D}\times _{N(\Delta )}T^1,\mathcal {C})$ spanned by the functors ![]() $F$ satisfying an analogue of (2.2.4), i.e. for every object
$F$ satisfying an analogue of (2.2.4), i.e. for every object ![]() $x\in \mathcal {D}$, let
$x\in \mathcal {D}$, let ![]() $[n_x]$ denote
$[n_x]$ denote ![]() $p(x)$ where
$p(x)$ where ![]() $p: \mathcal {D}\rightarrow N(\Delta )$ is the projection, then the natural morphism
$p: \mathcal {D}\rightarrow N(\Delta )$ is the projection, then the natural morphism
is an isomorphism for all ![]() $0\leq i\leq j\leq n_x$. We want to show that the middle arrow in (2.2.7) is a trivial Kan fibration, then this proves
$0\leq i\leq j\leq n_x$. We want to show that the middle arrow in (2.2.7) is a trivial Kan fibration, then this proves ![]() $\mathcal {C}^{\times,\Delta, 1}\overset {\sim }{\rightarrow }\mathcal {C}^{\times,\Delta }$ and it is surjective on vertices.
$\mathcal {C}^{\times,\Delta, 1}\overset {\sim }{\rightarrow }\mathcal {C}^{\times,\Delta }$ and it is surjective on vertices.
We will apply [Reference LurieLur09, 4.3.2.15] by showing that every functor ![]() $F: \mathcal {D}\times _{N(\Delta )}T\rightarrow \mathcal {C}$ has a right Kan extension to
$F: \mathcal {D}\times _{N(\Delta )}T\rightarrow \mathcal {C}$ has a right Kan extension to ![]() $\mathcal {D}\times _{N(\Delta )}T^1$, and
$\mathcal {D}\times _{N(\Delta )}T^1$, and ![]() $\mathrm {Maps}'(\mathcal {D}\times _{N(\Delta )}T^1,\mathcal {C})$ is the full subcategory of
$\mathrm {Maps}'(\mathcal {D}\times _{N(\Delta )}T^1,\mathcal {C})$ is the full subcategory of ![]() $\mathrm {Maps}(\mathcal {D}\times _{N(\Delta )}T^1,\mathcal {C})$ spanned by right Kan extensions of functors
$\mathrm {Maps}(\mathcal {D}\times _{N(\Delta )}T^1,\mathcal {C})$ spanned by right Kan extensions of functors ![]() $F: \mathcal {D}\times _{N(\Delta )}T\rightarrow \mathcal {C}$. For any object
$F: \mathcal {D}\times _{N(\Delta )}T\rightarrow \mathcal {C}$. For any object ![]() $(x, ([n_x],i\leq j))$ in
$(x, ([n_x],i\leq j))$ in ![]() $\mathcal {D}\times _{N(\Delta )}T^1$ with
$\mathcal {D}\times _{N(\Delta )}T^1$ with ![]() $j\geq i+2$, we have
$j\geq i+2$, we have
for every arrow ![]() $(x, ([n_x],i\leq j))\rightarrow (y, ([n_y],s\leq s+1))$ has a unique factorization
$(x, ([n_x],i\leq j))\rightarrow (y, ([n_y],s\leq s+1))$ has a unique factorization
for a unique ![]() $k\in [i,j-1]$, where the first map is defined by the identity on
$k\in [i,j-1]$, where the first map is defined by the identity on ![]() $x$ and the inclusion
$x$ and the inclusion ![]() $[k,k+1]\subset [i,j]$. Since
$[k,k+1]\subset [i,j]$. Since ![]() $(x, ([n_x],k\leq k+1))$ is the initial object in
$(x, ([n_x],k\leq k+1))$ is the initial object in ![]() $(\mathcal {D}\times _{N( \Delta )}T)_{(x, ([n_x],k\leq k+1))/}$, for any
$(\mathcal {D}\times _{N( \Delta )}T)_{(x, ([n_x],k\leq k+1))/}$, for any ![]() $F: \mathcal {D}\times _{N(\Delta )}T\rightarrow \mathcal {C}$, the limit of the induced functor
$F: \mathcal {D}\times _{N(\Delta )}T\rightarrow \mathcal {C}$, the limit of the induced functor ![]() $F_{(x, ([n_x],i\leq j))}:(\mathcal {D}\times _{N(\Delta )}T)_{(x, ([n_x],i\leq j))/}\rightarrow \mathcal {C}$ is isomorphic to
$F_{(x, ([n_x],i\leq j))}:(\mathcal {D}\times _{N(\Delta )}T)_{(x, ([n_x],i\leq j))/}\rightarrow \mathcal {C}$ is isomorphic to ![]() $\prod _{i\leq k\leq j-1}F(x, ([n_x],k\leq k+1))$, it follows that the middle map in (2.2.7) is a trivial Kan fibration.
$\prod _{i\leq k\leq j-1}F(x, ([n_x],k\leq k+1))$, it follows that the middle map in (2.2.7) is a trivial Kan fibration.
Lastly, since ![]() $R$ is surjective on vertices, a morphism
$R$ is surjective on vertices, a morphism ![]() $p: F\rightarrow F'$ is Cartesian in
$p: F\rightarrow F'$ is Cartesian in ![]() $\mathcal {C}^{\times,\Delta }$ if and only if it is the image of a Cartesian morphism through
$\mathcal {C}^{\times,\Delta }$ if and only if it is the image of a Cartesian morphism through ![]() $R$. This is clearly the condition (2.2.6).
$R$. This is clearly the condition (2.2.6).
One can define ![]() $\mathcal {C}^{\times,(\mathrm {Fin}_*)^{\rm op}}\rightarrow N(\mathrm {Fin}_*)^{\rm op}$ in a similar way. Let
$\mathcal {C}^{\times,(\mathrm {Fin}_*)^{\rm op}}\rightarrow N(\mathrm {Fin}_*)^{\rm op}$ in a similar way. Let ![]() $T^{1,\mathrm {Comm}}$ be the ordinary category consisting of objects
$T^{1,\mathrm {Comm}}$ be the ordinary category consisting of objects ![]() $(\langle n\rangle,S), S\subset \langle n\rangle ^{\circ }$, and morphisms
$(\langle n\rangle,S), S\subset \langle n\rangle ^{\circ }$, and morphisms ![]() $\alpha ^{\rm op}: (\langle n\rangle,S)\rightarrow (\langle m\rangle,S')$ given by a morphism
$\alpha ^{\rm op}: (\langle n\rangle,S)\rightarrow (\langle m\rangle,S')$ given by a morphism ![]() $\langle m\rangle \rightarrow \langle n\rangle$ in
$\langle m\rangle \rightarrow \langle n\rangle$ in ![]() $\mathrm {Fin}_*$ such that
$\mathrm {Fin}_*$ such that ![]() $\alpha ^{-1}(S)\supset S'$. The projection
$\alpha ^{-1}(S)\supset S'$. The projection ![]() $T^{1,\mathrm {Comm}}\rightarrow N(\mathrm {Fin}_*)^{\rm op}$ is a coCartesian fibration with a morphism
$T^{1,\mathrm {Comm}}\rightarrow N(\mathrm {Fin}_*)^{\rm op}$ is a coCartesian fibration with a morphism ![]() $\alpha ^{\rm op}: (\langle n\rangle,S)\rightarrow (\langle m\rangle,S')$ being coCartesian if and only if
$\alpha ^{\rm op}: (\langle n\rangle,S)\rightarrow (\langle m\rangle,S')$ being coCartesian if and only if ![]() $S'=\alpha ^{-1}(S)$. Let
$S'=\alpha ^{-1}(S)$. Let ![]() $T^{\mathrm {Comm}}$ be the full subcategory of
$T^{\mathrm {Comm}}$ be the full subcategory of ![]() $T^{1,\mathrm {Comm}}$ consisting of
$T^{1,\mathrm {Comm}}$ consisting of ![]() $(\langle n\rangle, S)$ where
$(\langle n\rangle, S)$ where ![]() $S$ contains exactly one element.
$S$ contains exactly one element.
Define ![]() $\mathcal {C}^{\times,(\mathrm {Fin}_*)^{\rm op}}$ over
$\mathcal {C}^{\times,(\mathrm {Fin}_*)^{\rm op}}$ over ![]() $N(\mathrm {Fin}_*)^{\rm op}$ to be the simplicial set characterized by that for any simplicial set
$N(\mathrm {Fin}_*)^{\rm op}$ to be the simplicial set characterized by that for any simplicial set ![]() $K$ over
$K$ over ![]() $N(\mathrm {Fin}_*)^{\rm op}$, we have
$N(\mathrm {Fin}_*)^{\rm op}$, we have
Then we have the commutative analogue of Proposition 2.5.
Proposition 2.6 The projection ![]() $\mathcal {C}^{\times,(\mathrm {Fin}_*)^{\rm op}}\rightarrow N(\mathrm {Fin}_*)^{\rm op}$ is a Cartesian fibration over
$\mathcal {C}^{\times,(\mathrm {Fin}_*)^{\rm op}}\rightarrow N(\mathrm {Fin}_*)^{\rm op}$ is a Cartesian fibration over ![]() $N(\mathrm {Fin}_*)^{\rm op}$ representing the Cartesian symmetric monoidal structure on
$N(\mathrm {Fin}_*)^{\rm op}$ representing the Cartesian symmetric monoidal structure on ![]() $\mathcal {C}$. A morphism
$\mathcal {C}$. A morphism ![]() $p: F\rightarrow F'$ is a Cartesian morphism over
$p: F\rightarrow F'$ is a Cartesian morphism over ![]() $\alpha ^{\rm op}:\langle n\rangle \rightarrow \langle m\rangle$ if and only if
$\alpha ^{\rm op}:\langle n\rangle \rightarrow \langle m\rangle$ if and only if
is an isomorphism for all ![]() $i\in \langle n\rangle ^\circ$.
$i\in \langle n\rangle ^\circ$.
2.3 Construction of (commutative) algebra objects of  $\mathrm {Corr}(\mathcal {C}^\times )$
$\mathrm {Corr}(\mathcal {C}^\times )$
From now on, we assume that ![]() $\mathcal {C}$ has the Cartesian (symmetric) monoidal structure, and
$\mathcal {C}$ has the Cartesian (symmetric) monoidal structure, and ![]() $\mathrm {Corr}(\mathcal {C})$ is endowed with the induced (symmetric) monoidal structure. Note that the latter is not Cartesian in general, for the final object in
$\mathrm {Corr}(\mathcal {C})$ is endowed with the induced (symmetric) monoidal structure. Note that the latter is not Cartesian in general, for the final object in ![]() $\mathrm {Corr}(\mathcal {C})$ is the initial object in
$\mathrm {Corr}(\mathcal {C})$ is the initial object in ![]() $\mathcal {C}$.
$\mathcal {C}$.
It is shown in [Reference Gaitsgory and RozenblyumGR17, Corollary 4.4.5, Chapter V.3] that every Segal object ![]() $C^\bullet$ of
$C^\bullet$ of ![]() $\mathcal {C}$ gives an algebra object in
$\mathcal {C}$ gives an algebra object in ![]() $\mathrm {Corr}(\mathcal {C})$. Here we give a more general construction of (commutative) algebra objects in
$\mathrm {Corr}(\mathcal {C})$. Here we give a more general construction of (commutative) algebra objects in ![]() $\mathrm {Corr}(\mathcal {C})$ out of simplicial or
$\mathrm {Corr}(\mathcal {C})$ out of simplicial or ![]() $\mathrm {Fin}_*$-objects in
$\mathrm {Fin}_*$-objects in ![]() $\mathcal {C}$ (see Theorem 2.8). Moreover, we provide a concise condition for defining a (right-lax) homomorphism between two (commutative) algebra objects constructed in this way (see Theorem 2.13). We expect that this construction gives ‘all’ the (commutative) algebra objects and (right-lax) homomorphisms between them in the sense of the equivalences in Remark 2.15. We will address this point in a separate note.
$\mathcal {C}$ (see Theorem 2.8). Moreover, we provide a concise condition for defining a (right-lax) homomorphism between two (commutative) algebra objects constructed in this way (see Theorem 2.13). We expect that this construction gives ‘all’ the (commutative) algebra objects and (right-lax) homomorphisms between them in the sense of the equivalences in Remark 2.15. We will address this point in a separate note.
Let ![]() $\pi _I: I\rightarrow N(\Delta )^{\rm op}$ (respectively,
$\pi _I: I\rightarrow N(\Delta )^{\rm op}$ (respectively, ![]() $\pi _I^\mathrm {Comm}: I^\mathrm {Comm}\rightarrow N(\mathrm {Fin}_*)$) be the coCartesian fibration (actually a left fibration) from the Grothendieck construction for
$\pi _I^\mathrm {Comm}: I^\mathrm {Comm}\rightarrow N(\mathrm {Fin}_*)$) be the coCartesian fibration (actually a left fibration) from the Grothendieck construction for ![]() $\mathrm {Seq}_\bullet (N(\Delta )^{\rm op}):N(\Delta )^{\rm op}\rightarrow \text {Sets}$ (respectively,
$\mathrm {Seq}_\bullet (N(\Delta )^{\rm op}):N(\Delta )^{\rm op}\rightarrow \text {Sets}$ (respectively, ![]() $\mathrm {Seq}_\bullet (N(\mathrm {Fin}_*)):N(\Delta )^{\rm op}\rightarrow \text {Sets}$). More explicitly, the set of objects of
$\mathrm {Seq}_\bullet (N(\mathrm {Fin}_*)):N(\Delta )^{\rm op}\rightarrow \text {Sets}$). More explicitly, the set of objects of ![]() $I$ is the union of discrete sets
$I$ is the union of discrete sets ![]() $\bigsqcup _{n}\mathrm {Seq}_n(N(\Delta )^{\rm op})$, and the morphisms are induced from the maps
$\bigsqcup _{n}\mathrm {Seq}_n(N(\Delta )^{\rm op})$, and the morphisms are induced from the maps ![]() $\mathrm {Seq}_{m}(N(\Delta )^{\rm op})\rightarrow \mathrm {Seq}_{n}(N(\Delta )^{\rm op})$, for
$\mathrm {Seq}_{m}(N(\Delta )^{\rm op})\rightarrow \mathrm {Seq}_{n}(N(\Delta )^{\rm op})$, for ![]() $[n]\rightarrow [m]$ in
$[n]\rightarrow [m]$ in ![]() $\Delta$.
$\Delta$.
The assignment
 \begin{align*} f_I: I^{\rm op}&\longrightarrow 1\text{-}\mathcal{C}\mathrm{at}^{\mathrm{ord}}, \\ ([n],s)&\mapsto ([n]\times[n]^{\rm op})^{\geq\mathrm{dgnl}}\times_{N(\Delta)}T, \end{align*}
\begin{align*} f_I: I^{\rm op}&\longrightarrow 1\text{-}\mathcal{C}\mathrm{at}^{\mathrm{ord}}, \\ ([n],s)&\mapsto ([n]\times[n]^{\rm op})^{\geq\mathrm{dgnl}}\times_{N(\Delta)}T, \end{align*}
in which the map ![]() $([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}\rightarrow N(\Delta )$ is the composition of the projection of
$([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}\rightarrow N(\Delta )$ is the composition of the projection of ![]() $([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}$ to the second factor with
$([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}$ to the second factor with ![]() $s^{\rm op}: (\Delta ^n)^{\rm op}\rightarrow N(\Delta )$ and
$s^{\rm op}: (\Delta ^n)^{\rm op}\rightarrow N(\Delta )$ and ![]() $f_I(\alpha )$ is the identity on the factors
$f_I(\alpha )$ is the identity on the factors ![]() $N(\Delta )$ and
$N(\Delta )$ and ![]() $T$ for any
$T$ for any ![]() $(\alpha : ([n],s)\rightarrow ([m], t))$ in
$(\alpha : ([n],s)\rightarrow ([m], t))$ in ![]() $I^{\rm op}$, gives a Cartesian fibration
$I^{\rm op}$, gives a Cartesian fibration
from the Grothendieck construction. Similarly, we have a Cartesian fibration
Consider the functors
 \begin{align} f_I^\mathcal{C}: I&\longrightarrow 1\text{-}\mathcal{C}\mathrm{at}, \\ ([n],s)&\mapsto \mathrm{Fun} (([n]\times[n]^{\rm op})^{\geq\mathrm{dgnl}}\times_{N(\Delta)}T,\mathcal{C}) \nonumber \end{align}
\begin{align} f_I^\mathcal{C}: I&\longrightarrow 1\text{-}\mathcal{C}\mathrm{at}, \\ ([n],s)&\mapsto \mathrm{Fun} (([n]\times[n]^{\rm op})^{\geq\mathrm{dgnl}}\times_{N(\Delta)}T,\mathcal{C}) \nonumber \end{align}
which is a composition of ![]() $f_I^{\rm op}$ with
$f_I^{\rm op}$ with ![]() $\mathrm {Fun}(-, \mathcal {C}): (1\text {-}\mathcal {C}\mathrm {at}^{\mathrm {ord}})^{\rm op}\rightarrow 1\text {-}\mathcal {C}\mathrm {at}$, and
$\mathrm {Fun}(-, \mathcal {C}): (1\text {-}\mathcal {C}\mathrm {at}^{\mathrm {ord}})^{\rm op}\rightarrow 1\text {-}\mathcal {C}\mathrm {at}$, and
 \begin{align} f_{\Delta^\bullet}^\mathcal{C}: N(\Delta)^{\rm op}&\longrightarrow1\text{-}\mathcal{C}\mathrm{at} \nonumber\\ [n]&\mapsto \coprod_{s\in \mathrm{Seq}_n(N(\Delta)^{\rm op})}\mathrm{Fun}(([n]\times[n]^{\rm op})^{\geq\mathrm{dgnl}}\times_{N(\Delta)}T,\mathcal{C})\simeq \mathrm{Fun}'([n]\times[n]^{\rm op})^{\geq\mathrm{dgnl}}, \mathcal{C}^{\times,\Delta}), \end{align}
\begin{align} f_{\Delta^\bullet}^\mathcal{C}: N(\Delta)^{\rm op}&\longrightarrow1\text{-}\mathcal{C}\mathrm{at} \nonumber\\ [n]&\mapsto \coprod_{s\in \mathrm{Seq}_n(N(\Delta)^{\rm op})}\mathrm{Fun}(([n]\times[n]^{\rm op})^{\geq\mathrm{dgnl}}\times_{N(\Delta)}T,\mathcal{C})\simeq \mathrm{Fun}'([n]\times[n]^{\rm op})^{\geq\mathrm{dgnl}}, \mathcal{C}^{\times,\Delta}), \end{align}
where ![]() $\mathrm {Fun}'([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\times,\Delta })$ was defined above (2.2.2). It is clear that
$\mathrm {Fun}'([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\times,\Delta })$ was defined above (2.2.2). It is clear that ![]() $f_\Delta ^\mathcal {C}$ is a left Kan extension of
$f_\Delta ^\mathcal {C}$ is a left Kan extension of ![]() $f_I^\mathcal {C}$ through the projection
$f_I^\mathcal {C}$ through the projection ![]() $\pi _I$.
$\pi _I$.
We state a lemma before proceeding further on the constructions. Assume ![]() $S=N(\mathcal {D})$ is the nerve of a small ordinary category
$S=N(\mathcal {D})$ is the nerve of a small ordinary category ![]() $\mathcal {D}$. Let
$\mathcal {D}$. Let ![]() $f: \mathcal {D}^{\rm op}\rightarrow \mathcal {S}\mathrm {et}_{\Delta }^+$ be a fibrant object in
$f: \mathcal {D}^{\rm op}\rightarrow \mathcal {S}\mathrm {et}_{\Delta }^+$ be a fibrant object in ![]() $(\mathcal {S}\mathrm {et}_{\Delta }^+)^{\mathcal {D}^{\rm op}}$. Let
$(\mathcal {S}\mathrm {et}_{\Delta }^+)^{\mathcal {D}^{\rm op}}$. Let ![]() $N_\bullet ^{+,op}(\mathcal {D}): (\mathcal {S}\mathrm {et}_{\Delta }^+)^{\mathcal {D}^{\rm op}}\rightarrow (\mathcal {S}\mathrm {et}_{\Delta }^+)_{/S}$ and
$N_\bullet ^{+,op}(\mathcal {D}): (\mathcal {S}\mathrm {et}_{\Delta }^+)^{\mathcal {D}^{\rm op}}\rightarrow (\mathcal {S}\mathrm {et}_{\Delta }^+)_{/S}$ and ![]() $N_\bullet ^{+}(\mathcal {D}): (\mathcal {S}\mathrm {et}_{\Delta }^+)^{\mathcal {D}}\rightarrow (\mathcal {S}\mathrm {et}_{\Delta }^+)_{/S}$ be the relative nerve functor as in [Reference LurieLur09, § 3.2.5]. Let
$N_\bullet ^{+}(\mathcal {D}): (\mathcal {S}\mathrm {et}_{\Delta }^+)^{\mathcal {D}}\rightarrow (\mathcal {S}\mathrm {et}_{\Delta }^+)_{/S}$ be the relative nerve functor as in [Reference LurieLur09, § 3.2.5]. Let ![]() $X^\natural \longrightarrow S$ denote
$X^\natural \longrightarrow S$ denote ![]() $N_f^{+,op}(\mathcal {D})\in (\mathcal {S}\mathrm {et}_{\Delta }^+)_{/S}$, and let
$N_f^{+,op}(\mathcal {D})\in (\mathcal {S}\mathrm {et}_{\Delta }^+)_{/S}$, and let ![]() $\mathcal {Z}^\natural \in \mathcal {S}\mathrm {et}_{\Delta }^+$ be an
$\mathcal {Z}^\natural \in \mathcal {S}\mathrm {et}_{\Delta }^+$ be an ![]() $\infty$-category. Here we use the notation following [Reference LurieLur09, Definition 3.1.1.8], that if
$\infty$-category. Here we use the notation following [Reference LurieLur09, Definition 3.1.1.8], that if ![]() $X\rightarrow S$ is a (co)Cartesian fibration, then
$X\rightarrow S$ is a (co)Cartesian fibration, then ![]() $X^\natural$ is the marked simplicial set with all its (co)Cartesian edges being marked. In particular, for an
$X^\natural$ is the marked simplicial set with all its (co)Cartesian edges being marked. In particular, for an ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {Z}$, an edge is marked in
$\mathcal {Z}$, an edge is marked in ![]() $\mathcal {Z}^\natural$ if and only if it is an isomorphism. Let
$\mathcal {Z}^\natural$ if and only if it is an isomorphism. Let ![]() $g: \mathcal {D}\rightarrow \mathcal {S}\mathrm {et}_{\Delta }^+$ denote the composition
$g: \mathcal {D}\rightarrow \mathcal {S}\mathrm {et}_{\Delta }^+$ denote the composition ![]() $\mathcal {D}\overset {f^{\rm op}}{\rightarrow } (\mathcal {S}\mathrm {et}_{\Delta }^+)^{\rm op}\overset {(Z^{\natural })^{(-)}}{\rightarrow } \mathcal {S}\mathrm {et}_{\Delta }^+$. We define
$\mathcal {D}\overset {f^{\rm op}}{\rightarrow } (\mathcal {S}\mathrm {et}_{\Delta }^+)^{\rm op}\overset {(Z^{\natural })^{(-)}}{\rightarrow } \mathcal {S}\mathrm {et}_{\Delta }^+$. We define
Following [Reference LurieLur09, Corollary 3.2.2.12], let ![]() $T_{\mathcal {Z}}^X$ be the simplicial set defined by the property
$T_{\mathcal {Z}}^X$ be the simplicial set defined by the property
then ![]() $T_{\mathcal {Z}}^X\rightarrow S$ is a coCartesian fibration and
$T_{\mathcal {Z}}^X\rightarrow S$ is a coCartesian fibration and ![]() $(T_{\mathcal {Z}}^{X})^{\natural }\in (\mathcal {S}\mathrm {et}_{\Delta }^+)_{/S}$ can be characterized by the property
$(T_{\mathcal {Z}}^{X})^{\natural }\in (\mathcal {S}\mathrm {et}_{\Delta }^+)_{/S}$ can be characterized by the property
Lemma 2.7 Under the above assumptions, there is a weak equivalence ![]() $(\mathcal {Z}^\natural )^{X^\natural }\longrightarrow (T_{\mathcal {Z}}^X)^\natural$ with respect to the coCartesian model structure on
$(\mathcal {Z}^\natural )^{X^\natural }\longrightarrow (T_{\mathcal {Z}}^X)^\natural$ with respect to the coCartesian model structure on ![]() $(\mathcal {S}\mathrm {et}_{\Delta }^+)_{/S}$.
$(\mathcal {S}\mathrm {et}_{\Delta }^+)_{/S}$.
Proof. We have a natural map in ![]() $(\mathcal {S}\mathrm {et}_{\Delta }^+)_{/S}$
$(\mathcal {S}\mathrm {et}_{\Delta }^+)_{/S}$
induced from the evaluation maps
for ![]() $j\in \mathcal {D}$. By the definition of
$j\in \mathcal {D}$. By the definition of ![]() $(T_\mathcal {Z}^X)^\natural$, this corresponds to a map
$(T_\mathcal {Z}^X)^\natural$, this corresponds to a map
in ![]() $(\mathcal {S}\mathrm {et}_{\Delta }^+)_{/S}$. Since both sides of (2.3.4) are fibrant objects in
$(\mathcal {S}\mathrm {et}_{\Delta }^+)_{/S}$. Since both sides of (2.3.4) are fibrant objects in ![]() $(\mathcal {S}\mathrm {et}_{\Delta }^+)_{/S}$ and the map induces isomorphisms on the fibers, (2.3.4) is a weak equivalence with respect to the coCartesian model structure on
$(\mathcal {S}\mathrm {et}_{\Delta }^+)_{/S}$ and the map induces isomorphisms on the fibers, (2.3.4) is a weak equivalence with respect to the coCartesian model structure on ![]() $(\mathcal {S}\mathrm {et}_{\Delta }^+)_{/S}$.
$(\mathcal {S}\mathrm {et}_{\Delta }^+)_{/S}$.
Now coming back to the construction of algebra objects, we let ![]() $(\mathcal {C}^\natural )^{\mathcal {T}^\natural }\rightarrow I$ denote the coCartesian fibration defined by
$(\mathcal {C}^\natural )^{\mathcal {T}^\natural }\rightarrow I$ denote the coCartesian fibration defined by ![]() $N_{f_I^\mathcal {C}}^+(I)$. Then Lemma 2.7 implies that
$N_{f_I^\mathcal {C}}^+(I)$. Then Lemma 2.7 implies that
 \begin{align}
\mathrm{Maps}_{I}(\mathcal{T}^\natural, (\mathcal{C}\times
I)^\natural)&\simeq\mathrm{Maps}_{I}(I^\natural,(\mathcal{C}^{\natural})^{{\mathcal{T}}^\natural})
\simeq
\mathrm{Maps}_{(\pi_I)_!I^\natural}((\pi_I)_!I^\natural,
(\pi_I)_!(\mathcal{C}^\natural)^{\mathcal{T}^\natural})\\
&\simeq
\mathrm{Maps}_{(1\text{-}\mathcal{C}\mathrm{at})^{\Delta^{\rm
op}}/_{\mathrm{Seq}_\bullet(N(\Delta)^{\rm
op})}}(\mathrm{Seq}_\bullet(N(\Delta)^{\rm op}),
f_{\Delta^\bullet}^\mathcal{C}). \nonumber
\end{align}
\begin{align}
\mathrm{Maps}_{I}(\mathcal{T}^\natural, (\mathcal{C}\times
I)^\natural)&\simeq\mathrm{Maps}_{I}(I^\natural,(\mathcal{C}^{\natural})^{{\mathcal{T}}^\natural})
\simeq
\mathrm{Maps}_{(\pi_I)_!I^\natural}((\pi_I)_!I^\natural,
(\pi_I)_!(\mathcal{C}^\natural)^{\mathcal{T}^\natural})\\
&\simeq
\mathrm{Maps}_{(1\text{-}\mathcal{C}\mathrm{at})^{\Delta^{\rm
op}}/_{\mathrm{Seq}_\bullet(N(\Delta)^{\rm
op})}}(\mathrm{Seq}_\bullet(N(\Delta)^{\rm op}),
f_{\Delta^\bullet}^\mathcal{C}). \nonumber
\end{align} There is a totally analogous construction of ![]() $f_I^\mathrm {Comm}, f_I^{\mathcal {C}, \mathrm {Comm}}$ and
$f_I^\mathrm {Comm}, f_I^{\mathcal {C}, \mathrm {Comm}}$ and ![]() $f_{\Delta }^{\mathcal {C}, \mathrm {Comm}}, \mathcal {T}^\mathrm {Comm}$ in which one makes the following replacement:
$f_{\Delta }^{\mathcal {C}, \mathrm {Comm}}, \mathcal {T}^\mathrm {Comm}$ in which one makes the following replacement:
 \begin{align*} & I\rightsquigarrow I^\mathrm{Comm},\ N(\Delta)\rightsquigarrow N(\mathrm{Fin}_*)^{\rm op},\ T\rightsquigarrow T^\mathrm{Comm}, \mathcal{C}^{\times,\Delta}\rightsquigarrow \mathcal{C}^{\times,(\mathrm{Fin}_*)^{\rm op}},\\ & f_{\Delta^\bullet}^\mathcal{C}\rightsquigarrow f_{\Delta^\bullet}^{\mathcal{C},\mathrm{Comm}}. \end{align*}
\begin{align*} & I\rightsquigarrow I^\mathrm{Comm},\ N(\Delta)\rightsquigarrow N(\mathrm{Fin}_*)^{\rm op},\ T\rightsquigarrow T^\mathrm{Comm}, \mathcal{C}^{\times,\Delta}\rightsquigarrow \mathcal{C}^{\times,(\mathrm{Fin}_*)^{\rm op}},\\ & f_{\Delta^\bullet}^\mathcal{C}\rightsquigarrow f_{\Delta^\bullet}^{\mathcal{C},\mathrm{Comm}}. \end{align*}
Recall that a morphism ![]() $f: [n]\rightarrow [m]$ in
$f: [n]\rightarrow [m]$ in ![]() $N(\Delta )$ (respectively,
$N(\Delta )$ (respectively, ![]() $f: \langle m\rangle \rightarrow \langle n\rangle$ in
$f: \langle m\rangle \rightarrow \langle n\rangle$ in ![]() $N(\mathrm {Fin}_*)$) is called active if
$N(\mathrm {Fin}_*)$) is called active if ![]() $[f(0), f(n)]=[0,m]$ (respectively,
$[f(0), f(n)]=[0,m]$ (respectively, ![]() $f^{-1}(*)=\{*\}$). A morphism
$f^{-1}(*)=\{*\}$). A morphism ![]() $f: [n]\rightarrow [m]$ in
$f: [n]\rightarrow [m]$ in ![]() $N(\Delta )$ (respectively,
$N(\Delta )$ (respectively, ![]() $f: \langle m\rangle \rightarrow \langle n\rangle$ in
$f: \langle m\rangle \rightarrow \langle n\rangle$ in ![]() $N(\mathrm {Fin}_*)$) is called inert if
$N(\mathrm {Fin}_*)$) is called inert if ![]() $f$ is of the form
$f$ is of the form ![]() $f(i)=i+k, 0\leq i\leq n$ for a fixed
$f(i)=i+k, 0\leq i\leq n$ for a fixed ![]() $k$ (respectively,
$k$ (respectively, ![]() $f^{-1}(i)$ has exactly one element for every
$f^{-1}(i)$ has exactly one element for every ![]() $i\in \langle n\rangle ^\circ$). It is clear that every inert morphism
$i\in \langle n\rangle ^\circ$). It is clear that every inert morphism ![]() $f: [n]\rightarrow [m]$ in
$f: [n]\rightarrow [m]$ in ![]() $N(\Delta )$ (respectively,
$N(\Delta )$ (respectively, ![]() $f: \langle m\rangle \rightarrow \langle n\rangle$ in
$f: \langle m\rangle \rightarrow \langle n\rangle$ in ![]() $N(\mathrm {Fin}_*)$) corresponds to a unique embedding
$N(\mathrm {Fin}_*)$) corresponds to a unique embedding ![]() $[n]\hookrightarrow [m]$ (respectively,
$[n]\hookrightarrow [m]$ (respectively, ![]() $\langle n\rangle ^\circ \hookrightarrow \langle m\rangle ^\circ$).
$\langle n\rangle ^\circ \hookrightarrow \langle m\rangle ^\circ$).
Theorem 2.8
(i) Given any simplicial object
 $C^\bullet$ in
$C^\bullet$ in  $\mathcal {C}$ such that for any active
$\mathcal {C}$ such that for any active  $f: [n]\rightarrow [m]$ in
$f: [n]\rightarrow [m]$ in  $N(\Delta )$ and
$N(\Delta )$ and  $0\leq j\leq n-1$, the following square
(2.3.6)is Cartesian in
$0\leq j\leq n-1$, the following square
(2.3.6)is Cartesian in
 $\mathcal {C}$, where the vertical morphisms are induced by
$\mathcal {C}$, where the vertical morphisms are induced by  $f$ and the horizontal morphisms are induced from the inert morphisms
$f$ and the horizontal morphisms are induced from the inert morphisms  $[i,i+1]\hookrightarrow [n]$,
$[i,i+1]\hookrightarrow [n]$,  $[f(i),f(i+1)]\hookrightarrow [m]$, then
$[f(i),f(i+1)]\hookrightarrow [m]$, then  $C^\bullet$ naturally induces an associative algebra object in
$C^\bullet$ naturally induces an associative algebra object in  $\mathrm {Corr}(\mathcal {C}^\times )$ via (2.3.5).
$\mathrm {Corr}(\mathcal {C}^\times )$ via (2.3.5).(ii) Given any functor
 $C^\bullet : N(\mathrm {Fin}_*)\longrightarrow \mathcal {C}$ such that for any active
$C^\bullet : N(\mathrm {Fin}_*)\longrightarrow \mathcal {C}$ such that for any active  $f: \langle m\rangle \longrightarrow \langle n\rangle$, the following diagram
(2.3.7)is Cartesian in
$f: \langle m\rangle \longrightarrow \langle n\rangle$, the following diagram
(2.3.7)is Cartesian in
 $\mathcal {C}$, where the vertical morphisms are induced by
$\mathcal {C}$, where the vertical morphisms are induced by  $f$ and the horizontal morphisms are induced from the inert morphisms corresponding to the embeddings
$f$ and the horizontal morphisms are induced from the inert morphisms corresponding to the embeddings  $\{i\}\hookrightarrow \langle n\rangle$,
$\{i\}\hookrightarrow \langle n\rangle$,  $f^{-1}(i)\hookrightarrow \langle m\rangle$, then
$f^{-1}(i)\hookrightarrow \langle m\rangle$, then  $C^\bullet$ naturally induces a commutative algebra object in
$C^\bullet$ naturally induces a commutative algebra object in  $\mathrm {Corr}(\mathcal {C}^\times )$ via the commutative version of (2.3.5).
$\mathrm {Corr}(\mathcal {C}^\times )$ via the commutative version of (2.3.5).
Proof. (i) In view of (2.3.5), we just need to construct an element in ![]() $\mathrm {Hom}_I(\mathcal {T}^\natural, \mathcal {C}^\natural \times I)$, and check that its image in the rightmost term gives a section of
$\mathrm {Hom}_I(\mathcal {T}^\natural, \mathcal {C}^\natural \times I)$, and check that its image in the rightmost term gives a section of ![]() $\mathbf {Corr}(\mathcal {C})^{\otimes,\Delta ^{\rm op}}\rightarrow N(\Delta )^{\rm op}$ satisfying the properties required for an algebra object.
$\mathbf {Corr}(\mathcal {C})^{\otimes,\Delta ^{\rm op}}\rightarrow N(\Delta )^{\rm op}$ satisfying the properties required for an algebra object.
First, there is a natural functor ![]() $F_{\mathcal {T},\Delta ^{\rm op}}: \mathcal {T}\longrightarrow N(\Delta )^{\rm op}$ given by
$F_{\mathcal {T},\Delta ^{\rm op}}: \mathcal {T}\longrightarrow N(\Delta )^{\rm op}$ given by
in which ![]() $s_{j,i}: s(j)\rightarrow s(i), j\geq i$ is the morphism in
$s_{j,i}: s(j)\rightarrow s(i), j\geq i$ is the morphism in ![]() $N(\Delta )$ determined by
$N(\Delta )$ determined by ![]() $s$, (2.3.9) represents a morphism
$s$, (2.3.9) represents a morphism ![]() $\hat {\alpha }:([n],s,(i_1,j_1), u_1\leq u_1+1)\rightarrow ([m],t,(i_2,j_2), u_2\leq u_2+1)$ in
$\hat {\alpha }:([n],s,(i_1,j_1), u_1\leq u_1+1)\rightarrow ([m],t,(i_2,j_2), u_2\leq u_2+1)$ in ![]() $\mathcal {T}$ consisting of the data of a morphism
$\mathcal {T}$ consisting of the data of a morphism ![]() $\alpha ^{\rm op}$ in
$\alpha ^{\rm op}$ in ![]() $N(\Delta )$, and the relations
$N(\Delta )$, and the relations ![]() $t(j)=s(\alpha ^{\rm op}(j))$,
$t(j)=s(\alpha ^{\rm op}(j))$, ![]() $t_{a,b}=s_{\alpha ^{\rm op}(a), \alpha ^{\rm op}(b)}$,
$t_{a,b}=s_{\alpha ^{\rm op}(a), \alpha ^{\rm op}(b)}$, ![]() $i_1\leq \alpha ^{\rm op}(i_2)\leq \alpha ^{\rm op}(j_2)\leq j_1$ and
$i_1\leq \alpha ^{\rm op}(i_2)\leq \alpha ^{\rm op}(j_2)\leq j_1$ and ![]() $[u_2,u_2+1]\subset [s_{j_1,\alpha ^{\rm op}(j_2)}(u_1),s_{j_1,\alpha ^{\rm op}(j_2)}(u_1+1)]$. The morphism (2.3.10) in
$[u_2,u_2+1]\subset [s_{j_1,\alpha ^{\rm op}(j_2)}(u_1),s_{j_1,\alpha ^{\rm op}(j_2)}(u_1+1)]$. The morphism (2.3.10) in ![]() $N(\Delta )^{\rm op}$ comes from the composition
$N(\Delta )^{\rm op}$ comes from the composition
 \begin{align*} &[s_{\alpha^{\rm op}(j_2),\alpha^{\rm op}(i_2)}(u_2),s_{\alpha^{\rm op}(j_2),\alpha^{\rm op}(i_2)}(u_2+1)]\hookrightarrow [s_{j_1,\alpha^{\rm op}(i_2)}(u_1),s_{j_1,\alpha^{\rm op}(i_2)}(u_1+1)]\\ &\overset{s_{\alpha^{\rm op}(i_2),i_1}}{\longrightarrow} [s_{j_1,i_1}(u_1),s_{j_1,i_1}(u_1+1)] \end{align*}
\begin{align*} &[s_{\alpha^{\rm op}(j_2),\alpha^{\rm op}(i_2)}(u_2),s_{\alpha^{\rm op}(j_2),\alpha^{\rm op}(i_2)}(u_2+1)]\hookrightarrow [s_{j_1,\alpha^{\rm op}(i_2)}(u_1),s_{j_1,\alpha^{\rm op}(i_2)}(u_1+1)]\\ &\overset{s_{\alpha^{\rm op}(i_2),i_1}}{\longrightarrow} [s_{j_1,i_1}(u_1),s_{j_1,i_1}(u_1+1)] \end{align*}
in ![]() $N(\Delta )$.
$N(\Delta )$.
It is not hard to check that the assignment (2.3.10) is compatible with compositions. If we have two morphisms
then we have the relations
Then ![]() $(F_{\mathcal {T},\Delta ^{\rm op}}(\hat {\beta })\circ F_{\mathcal {T},\Delta ^{\rm op}}(\hat {\alpha }))^{\rm op}$ in
$(F_{\mathcal {T},\Delta ^{\rm op}}(\hat {\beta })\circ F_{\mathcal {T},\Delta ^{\rm op}}(\hat {\alpha }))^{\rm op}$ in ![]() $N(\Delta )$ is the same as the composition
$N(\Delta )$ is the same as the composition
 \begin{align*} &[t_{\beta^{\rm op}(j_3),\beta^{\rm op}(i_3)}(u_3), t_{\beta^{\rm op}(j_3),\beta^{\rm op}(i_3)}(u_3+1)]\hookrightarrow [t_{j_2,\beta^{\rm op}(i_3)}(u_2),t_{j_2,\beta^{\rm op}(i_3)}(u_2+1)]\\ &\overset{t_{\beta^{\rm op}(i_3), i_2}}{\longrightarrow}[t_{j_2,i_2}(u_2),t_{j_2,i_2}(u_2+1)]=[s_{\alpha^{\rm op}(j_2)\alpha^{\rm op}(i_2)}(u_2),s_{\alpha^{\rm op}(j_2),\alpha^{\rm op}(i_2)}(u_2+1)]\\ &\hookrightarrow [s_{j_1,\alpha^{\rm op}(i_2)}(u_1), s_{j_1,\alpha^{\rm op}(i_2)}(u_1+1)]\overset{s_{\alpha^{\rm op}(i_2), i_1}}{\longrightarrow}[s_{j_1,i_1}(u_1),s_{j_1,i_1}(u_1+1)], \end{align*}
\begin{align*} &[t_{\beta^{\rm op}(j_3),\beta^{\rm op}(i_3)}(u_3), t_{\beta^{\rm op}(j_3),\beta^{\rm op}(i_3)}(u_3+1)]\hookrightarrow [t_{j_2,\beta^{\rm op}(i_3)}(u_2),t_{j_2,\beta^{\rm op}(i_3)}(u_2+1)]\\ &\overset{t_{\beta^{\rm op}(i_3), i_2}}{\longrightarrow}[t_{j_2,i_2}(u_2),t_{j_2,i_2}(u_2+1)]=[s_{\alpha^{\rm op}(j_2)\alpha^{\rm op}(i_2)}(u_2),s_{\alpha^{\rm op}(j_2),\alpha^{\rm op}(i_2)}(u_2+1)]\\ &\hookrightarrow [s_{j_1,\alpha^{\rm op}(i_2)}(u_1), s_{j_1,\alpha^{\rm op}(i_2)}(u_1+1)]\overset{s_{\alpha^{\rm op}(i_2), i_1}}{\longrightarrow}[s_{j_1,i_1}(u_1),s_{j_1,i_1}(u_1+1)], \end{align*}
and ![]() $(F_{\mathcal {T},\Delta ^{\rm op}}(\hat {\beta }\hat {\alpha }))^{\rm op}$ is the composition
$(F_{\mathcal {T},\Delta ^{\rm op}}(\hat {\beta }\hat {\alpha }))^{\rm op}$ is the composition
 \begin{align*} &[t_{\beta^{\rm op}(j_3),\beta^{\rm op}(i_3)}(u_3), t_{\beta^{\rm op}(j_3),\beta^{\rm op}(i_3)}(u_3+1)]\hookrightarrow [s_{j_1,(\beta\alpha)^{\rm op}(i_3)}(u_1), s_{j_1,(\beta\alpha)^{\rm op}(i_3)}(u_1+1)]\\ &\overset{s_{(\beta\alpha)^{\rm op}(i_3)},i_1}{\longrightarrow}[s_{j_1,i_1}(u_1),s_{j_1,i_1}(u_1+1)]. \end{align*}
\begin{align*} &[t_{\beta^{\rm op}(j_3),\beta^{\rm op}(i_3)}(u_3), t_{\beta^{\rm op}(j_3),\beta^{\rm op}(i_3)}(u_3+1)]\hookrightarrow [s_{j_1,(\beta\alpha)^{\rm op}(i_3)}(u_1), s_{j_1,(\beta\alpha)^{\rm op}(i_3)}(u_1+1)]\\ &\overset{s_{(\beta\alpha)^{\rm op}(i_3)},i_1}{\longrightarrow}[s_{j_1,i_1}(u_1),s_{j_1,i_1}(u_1+1)]. \end{align*}
Now it is clear that ![]() $(F_{\mathcal {T},\Delta ^{\rm op}}(\hat {\beta })\circ F_{\mathcal {T},\Delta ^{\rm op}}(\hat {\alpha }))^{\rm op}=(F_{\mathcal {T},\Delta ^{\rm op}}(\hat {\beta }\hat {\alpha }))^{\rm op}$.
$(F_{\mathcal {T},\Delta ^{\rm op}}(\hat {\beta })\circ F_{\mathcal {T},\Delta ^{\rm op}}(\hat {\alpha }))^{\rm op}=(F_{\mathcal {T},\Delta ^{\rm op}}(\hat {\beta }\hat {\alpha }))^{\rm op}$.
Consider the functor ![]() $F_{C^\bullet }: \mathcal {T}\rightarrow \mathcal {C}$ from the composition
$F_{C^\bullet }: \mathcal {T}\rightarrow \mathcal {C}$ from the composition
A morphism ![]() $\hat {\alpha }$ (2.3.9) in
$\hat {\alpha }$ (2.3.9) in ![]() $\mathcal {T}$ is Cartesian over
$\mathcal {T}$ is Cartesian over ![]() $I$ if and only if
$I$ if and only if ![]() $i_1=\alpha ^{\rm op}(i_2), j_1=\alpha ^{\rm op}(j_2)$ and
$i_1=\alpha ^{\rm op}(i_2), j_1=\alpha ^{\rm op}(j_2)$ and ![]() $u_1=u_2$, so
$u_1=u_2$, so ![]() $F_{C^\bullet }$ sends a Cartesian morphism in
$F_{C^\bullet }$ sends a Cartesian morphism in ![]() $\mathcal {T}$ over
$\mathcal {T}$ over ![]() $I$ to an isomorphism in
$I$ to an isomorphism in ![]() $\mathcal {C}$ and, therefore, it belongs to
$\mathcal {C}$ and, therefore, it belongs to ![]() $\mathrm {Hom}_I(\mathcal {T}^\natural, \mathcal {C}^\natural \times I)$, whose image in
$\mathrm {Hom}_I(\mathcal {T}^\natural, \mathcal {C}^\natural \times I)$, whose image in ![]() $\mathrm {Hom}_I(I^\natural, (\mathcal {C}^\natural )^{\mathcal {T}^{\natural }})$ will be denoted by
$\mathrm {Hom}_I(I^\natural, (\mathcal {C}^\natural )^{\mathcal {T}^{\natural }})$ will be denoted by ![]() $F_{C^\bullet }$ as well. For any
$F_{C^\bullet }$ as well. For any ![]() $([n], s)\in I^\natural$,
$([n], s)\in I^\natural$, ![]() $F_{C^\bullet }([n], s)$ is the functor in
$F_{C^\bullet }([n], s)$ is the functor in ![]() $\mathrm {Fun}(([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}\times _{N(\Delta )}T,\mathcal {C})$ that sends
$\mathrm {Fun}(([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}\times _{N(\Delta )}T,\mathcal {C})$ that sends ![]() $([n], s,(i,j), u\leq u+1)$ to
$([n], s,(i,j), u\leq u+1)$ to ![]() $C^{[s_{j,i}(u), s_{j,i}(u+1)]}$. We check that
$C^{[s_{j,i}(u), s_{j,i}(u+1)]}$. We check that ![]() $F_{C^\bullet }([n], s)$ satisfies the condition (Obj) in § 2.2 for any
$F_{C^\bullet }([n], s)$ satisfies the condition (Obj) in § 2.2 for any ![]() $([n],s)$, which would imply that the image of
$([n],s)$, which would imply that the image of ![]() $F_{C^\bullet }$ in
$F_{C^\bullet }$ in ![]() $\mathrm {Hom}_{(1\text {-}\mathcal {C}\mathrm {at})^{\Delta ^{\rm op}}/_{\mathrm {Seq}_\bullet (N(\Delta )^{\rm op})}}(\mathrm {Seq}_\bullet (N(\Delta )^{\rm op}), f_\Delta ^\mathcal {C})$ corresponds to a functor from
$\mathrm {Hom}_{(1\text {-}\mathcal {C}\mathrm {at})^{\Delta ^{\rm op}}/_{\mathrm {Seq}_\bullet (N(\Delta )^{\rm op})}}(\mathrm {Seq}_\bullet (N(\Delta )^{\rm op}), f_\Delta ^\mathcal {C})$ corresponds to a functor from ![]() $N(\Delta )^{\rm op}$ to
$N(\Delta )^{\rm op}$ to ![]() $\mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}$ over
$\mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}$ over ![]() $N(\Delta )^{\rm op}$.
$N(\Delta )^{\rm op}$.
The condition (Obj) is equivalent to the following diagram

being Cartesian in ![]() $\mathcal {C}$ for all
$\mathcal {C}$ for all ![]() $i_1\leq i_2\leq j_2\leq j_1$ and
$i_1\leq i_2\leq j_2\leq j_1$ and ![]() $0\leq u\leq u+1\leq s(j_1)$. It can be further reduced to the case when
$0\leq u\leq u+1\leq s(j_1)$. It can be further reduced to the case when ![]() $i_2=j_2$. Then the diagram fits into (2.3.6) and all diagrams (2.3.6) occur in this way, and thus the assumption in the theorem guarantees that
$i_2=j_2$. Then the diagram fits into (2.3.6) and all diagrams (2.3.6) occur in this way, and thus the assumption in the theorem guarantees that ![]() $F_{C^\bullet }$ gives a section of
$F_{C^\bullet }$ gives a section of ![]() $p_{\mathbf {Corr}(\mathcal {C})}$. Since
$p_{\mathbf {Corr}(\mathcal {C})}$. Since ![]() $N(\Delta )^{\rm op}$ is a 1-category, the condition (Mor) is vacuous.
$N(\Delta )^{\rm op}$ is a 1-category, the condition (Mor) is vacuous.
The last thing we need to check is that the section sends any inert morphism ![]() $\alpha ^{\rm op}: [n]\rightarrow [m]$ in
$\alpha ^{\rm op}: [n]\rightarrow [m]$ in ![]() $N(\Delta )$ to a 2-coCartesian morphism. By construction,
$N(\Delta )$ to a 2-coCartesian morphism. By construction, ![]() $F_{C^\bullet }([1], \alpha )$ is determined by the collection of diagrams
$F_{C^\bullet }([1], \alpha )$ is determined by the collection of diagrams

for all ![]() $0\leq u< n$. The condition that
$0\leq u< n$. The condition that ![]() $\alpha ^{\rm op}$ is inert implies that
$\alpha ^{\rm op}$ is inert implies that ![]() $[\alpha ^{\rm op}(u),\alpha ^{\rm op}(u+1)]$ is of length one, so the horizontal and vertical arrows are isomorphisms in
$[\alpha ^{\rm op}(u),\alpha ^{\rm op}(u+1)]$ is of length one, so the horizontal and vertical arrows are isomorphisms in ![]() $\mathcal {C}$ and it corresponds to a 2-coCartesian morphism in
$\mathcal {C}$ and it corresponds to a 2-coCartesian morphism in ![]() $\mathbf {Corr}(\mathcal {C})^{\otimes,\Delta ^{\rm op}}$ as desired.
$\mathbf {Corr}(\mathcal {C})^{\otimes,\Delta ^{\rm op}}$ as desired.
(ii) The proof is very similar to that of part (i). There is a natural functor
 \begin{align} & F_{\mathcal{T}^\mathrm{Comm}, \mathrm{Fin}_*}: \mathcal{T}^\mathrm{Comm}\longrightarrow N(\mathrm{Fin}_*)\\ &([n], s,(i,j), u)\mapsto s_{i,j}^{-1}(u)\sqcup\{*\}\nonumber\\ &(\alpha^{\rm op}: [n]\leftarrow [m], s\rightarrow t, (i_1,j_1)\rightarrow (\alpha^{\rm op}(i_2), \alpha^{\rm op}(j_2)), u_2\in s_{\alpha^{\rm op}(j_2),j_1}^{-1}(u_1))\nonumber\\ &\mapsto (s_{i_1,j_1}^{-1}(u_1)\sqcup\{*\}\rightarrow t_{i_2,j_2}^{-1}(u_2)\sqcup\{*\}), \nonumber \end{align}
\begin{align} & F_{\mathcal{T}^\mathrm{Comm}, \mathrm{Fin}_*}: \mathcal{T}^\mathrm{Comm}\longrightarrow N(\mathrm{Fin}_*)\\ &([n], s,(i,j), u)\mapsto s_{i,j}^{-1}(u)\sqcup\{*\}\nonumber\\ &(\alpha^{\rm op}: [n]\leftarrow [m], s\rightarrow t, (i_1,j_1)\rightarrow (\alpha^{\rm op}(i_2), \alpha^{\rm op}(j_2)), u_2\in s_{\alpha^{\rm op}(j_2),j_1}^{-1}(u_1))\nonumber\\ &\mapsto (s_{i_1,j_1}^{-1}(u_1)\sqcup\{*\}\rightarrow t_{i_2,j_2}^{-1}(u_2)\sqcup\{*\}), \nonumber \end{align}
in which ![]() $s_{i,j}: s(i)\rightarrow s(j), i\leq j$ is a morphism in
$s_{i,j}: s(i)\rightarrow s(j), i\leq j$ is a morphism in ![]() $N(\mathrm {Fin}_*)$, the second line represents a morphism
$N(\mathrm {Fin}_*)$, the second line represents a morphism ![]() $\hat {\alpha }: ([n], s,(i_1,j_1), u_1)\rightarrow ([m], t,(i_2,j_2), u_2)$ consisting of the data of a morphism
$\hat {\alpha }: ([n], s,(i_1,j_1), u_1)\rightarrow ([m], t,(i_2,j_2), u_2)$ consisting of the data of a morphism ![]() $\alpha ^{\rm op}: [n]\leftarrow [m]$ in
$\alpha ^{\rm op}: [n]\leftarrow [m]$ in ![]() $N(\Delta )$,
$N(\Delta )$, ![]() $t_{a,b}=s_{\alpha ^{\rm op}(a),\alpha ^{\rm op}(b)},\ i_1\leq \alpha ^{\rm op}(i_2)\leq \alpha ^{\rm op}(j_2)\leq j_1$ and
$t_{a,b}=s_{\alpha ^{\rm op}(a),\alpha ^{\rm op}(b)},\ i_1\leq \alpha ^{\rm op}(i_2)\leq \alpha ^{\rm op}(j_2)\leq j_1$ and ![]() $u_2\in s_{\alpha ^{\rm op}(j_2),j_1}^{-1}(u_1)$. The morphism
$u_2\in s_{\alpha ^{\rm op}(j_2),j_1}^{-1}(u_1)$. The morphism ![]() $s_{i_1,j_1}^{-1}(u_1)\sqcup \{*\}\rightarrow t_{i_2,j_2}^{-1}(u_2)\sqcup \{*\}$ comes from the composition
$s_{i_1,j_1}^{-1}(u_1)\sqcup \{*\}\rightarrow t_{i_2,j_2}^{-1}(u_2)\sqcup \{*\}$ comes from the composition
in which ![]() $\rho$ is the inert morphism that is the right inverse to the inclusion
$\rho$ is the inert morphism that is the right inverse to the inclusion ![]() $s_{i_1,\alpha ^{\rm op}(j_2)}^{-1}(u_2)\sqcup \{*\}\hookrightarrow s_{i_1,j_1}^{-1}(u_1)\sqcup \{*\}$. It is straightforward to check that
$s_{i_1,\alpha ^{\rm op}(j_2)}^{-1}(u_2)\sqcup \{*\}\hookrightarrow s_{i_1,j_1}^{-1}(u_1)\sqcup \{*\}$. It is straightforward to check that ![]() $F_{\mathcal {T}^\mathrm {Comm},\mathrm {Fin}_*}$ is compatible with compositions. The remaining steps of the proof are direct analogues of those for part (i).
$F_{\mathcal {T}^\mathrm {Comm},\mathrm {Fin}_*}$ is compatible with compositions. The remaining steps of the proof are direct analogues of those for part (i).
Recall that a simplicial object ![]() $C^\bullet$ in
$C^\bullet$ in ![]() $\mathcal {C}$ (that admits finite limits) is called a Segal object if the morphism
$\mathcal {C}$ (that admits finite limits) is called a Segal object if the morphism
induced from the ![]() $n$ distinct inert morphisms
$n$ distinct inert morphisms ![]() $[1]\hookrightarrow [n]$ is an isomorphism in
$[1]\hookrightarrow [n]$ is an isomorphism in ![]() $\mathcal {C}$.
$\mathcal {C}$.
Similarly, we say a functor ![]() $C^\bullet : N(\mathrm {Fin}_*)\rightarrow \mathcal {C}$ is a commutative Segal object, if for any
$C^\bullet : N(\mathrm {Fin}_*)\rightarrow \mathcal {C}$ is a commutative Segal object, if for any ![]() $m$, the diagram
$m$, the diagram

associated with the ![]() $m$ distinct inert morphisms
$m$ distinct inert morphisms ![]() $\alpha _j: \langle m\rangle \rightarrow \langle 1\rangle, \alpha _j^{-1}(1)=j$, is a Cartesian diagram.
$\alpha _j: \langle m\rangle \rightarrow \langle 1\rangle, \alpha _j^{-1}(1)=j$, is a Cartesian diagram.
Corollary 2.9 Let ![]() $\mathcal {C}$ be an
$\mathcal {C}$ be an ![]() $(\infty,1)$-category which admits finite limits. Then every (commutative) Segal object
$(\infty,1)$-category which admits finite limits. Then every (commutative) Segal object ![]() $C^\bullet$ in
$C^\bullet$ in ![]() $\mathcal {C}$ naturally induces an (commutative) algebra object in
$\mathcal {C}$ naturally induces an (commutative) algebra object in ![]() $\mathrm {Corr}(\mathcal {C}^\times )$ via (2.3.5).
$\mathrm {Corr}(\mathcal {C}^\times )$ via (2.3.5).
Remark 2.10 For each ![]() $X\in \mathcal {C}^\times$, the constant
$X\in \mathcal {C}^\times$, the constant ![]() $\mathrm {Fin}_*$-object mapping to
$\mathrm {Fin}_*$-object mapping to ![]() $X$ in
$X$ in ![]() $\mathcal {C}$, denoted by
$\mathcal {C}$, denoted by ![]() $X^{\mathrm {const}, \bullet }$, gives a commutative Segal object and so a commutative algebra object in
$X^{\mathrm {const}, \bullet }$, gives a commutative Segal object and so a commutative algebra object in ![]() $\mathrm {Corr}(\mathcal {C})$, by Corollary 2.9.
$\mathrm {Corr}(\mathcal {C})$, by Corollary 2.9.
2.4 Construction of (right-lax) algebra homomorphisms in  $\mathbf {Corr}(\mathcal {C}^\times )$
$\mathbf {Corr}(\mathcal {C}^\times )$
Let ![]() ${\bigcirc{\kern-6pt \star}}$ be the Gray tensor product of two
${\bigcirc{\kern-6pt \star}}$ be the Gray tensor product of two ![]() $(\infty,2)$-categories (cf. [Reference Gaitsgory and RozenblyumGR17, Chapter A.1, § 3.2]), which agrees with the usual Gray product in the case of ordinary 2-categories. We have a description of
$(\infty,2)$-categories (cf. [Reference Gaitsgory and RozenblyumGR17, Chapter A.1, § 3.2]), which agrees with the usual Gray product in the case of ordinary 2-categories. We have a description of ![]() $\mathrm {Seq}_\bullet (N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}} [1])$:
$\mathrm {Seq}_\bullet (N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}} [1])$: ![]() $\mathrm {Seq}_k(N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}} [1])$ is an ordinary
$\mathrm {Seq}_k(N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}} [1])$ is an ordinary ![]() $1$-categoryFootnote 7 consisting of objects
$1$-categoryFootnote 7 consisting of objects ![]() $(\alpha,\beta ;\tau _0,\tau _1)$
$(\alpha,\beta ;\tau _0,\tau _1)$

where ![]() $[a]_\epsilon$ means the object
$[a]_\epsilon$ means the object ![]() $([a],\epsilon )\in \text {Obj}(N(\Delta )^{\rm op}\times [1])= \text {Obj}([ N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}} [1]),\ \epsilon =0,1$ (note that the marked morphisms
$([a],\epsilon )\in \text {Obj}(N(\Delta )^{\rm op}\times [1])= \text {Obj}([ N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}} [1]),\ \epsilon =0,1$ (note that the marked morphisms ![]() $\alpha _{i,j},\beta _{i,j}$ are in
$\alpha _{i,j},\beta _{i,j}$ are in ![]() $N(\Delta )$). Here we allow
$N(\Delta )$). Here we allow ![]() $\mu =0$ and
$\mu =0$ and ![]() $\mu =k+1$, so then
$\mu =k+1$, so then ![]() $\tau _0,\tau _1=\emptyset$. For two objects
$\tau _0,\tau _1=\emptyset$. For two objects ![]() $(\alpha,\beta ;\tau _0,\tau _1)$ and
$(\alpha,\beta ;\tau _0,\tau _1)$ and ![]() $(\alpha,\beta ;\tau '_0,\tau '_1)$, a morphism from the former to the latter is corresponding to a map
$(\alpha,\beta ;\tau '_0,\tau '_1)$, a morphism from the former to the latter is corresponding to a map ![]() $\varphi :[\xi ']\rightarrow [\xi ]$ in
$\varphi :[\xi ']\rightarrow [\xi ]$ in ![]() $N(\Delta )$ such that the following diagram commutes.
$N(\Delta )$ such that the following diagram commutes.

Here is a picture illustrating a morphism ![]() $(\alpha,\beta ;\tau _0,\tau _1)\rightarrow (\alpha,\beta ;\tau _0',\tau _1')$ (the upper right and lower left arrows indicate morphisms in
$(\alpha,\beta ;\tau _0,\tau _1)\rightarrow (\alpha,\beta ;\tau _0',\tau _1')$ (the upper right and lower left arrows indicate morphisms in ![]() $N(\Delta )^{\rm op}$).
$N(\Delta )^{\rm op}$).

For a map ![]() $\sigma : [\ell ]\rightarrow [k]$ in
$\sigma : [\ell ]\rightarrow [k]$ in ![]() $N(\Delta )$, the functor
$N(\Delta )$, the functor ![]() $\sigma ^*: \mathrm {Seq}_k(N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1])\rightarrow \mathrm {Seq}_\ell (N(\Delta )^{\textrm {op}}{\bigcirc{\kern-6pt \star}}[1])$ sends an object
$\sigma ^*: \mathrm {Seq}_k(N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1])\rightarrow \mathrm {Seq}_\ell (N(\Delta )^{\textrm {op}}{\bigcirc{\kern-6pt \star}}[1])$ sends an object ![]() $(\alpha, \beta, \tau _0,\tau _1)$ to
$(\alpha, \beta, \tau _0,\tau _1)$ to ![]() $\sigma ^*(\alpha,\beta ;\tau _0,\tau _1)$ defined by:
$\sigma ^*(\alpha,\beta ;\tau _0,\tau _1)$ defined by:
(1)
 $(\sigma ^*\alpha,\emptyset ;\emptyset, \emptyset )$ if
$(\sigma ^*\alpha,\emptyset ;\emptyset, \emptyset )$ if  $\sigma (\ell )\leq \mu -1$;
$\sigma (\ell )\leq \mu -1$;(2)
 $((\sigma |_{[0,\nu -1]})^*\alpha, (\sigma |_{[\nu,\ell ]})^*\beta ; \alpha _{\mu -1,\sigma (\nu -1)}\circ \tau _0, \tau _1\circ \beta _{\sigma (\nu )-\mu, 0})$, if there exists
$((\sigma |_{[0,\nu -1]})^*\alpha, (\sigma |_{[\nu,\ell ]})^*\beta ; \alpha _{\mu -1,\sigma (\nu -1)}\circ \tau _0, \tau _1\circ \beta _{\sigma (\nu )-\mu, 0})$, if there exists  $\nu \in [\ell ]$ such that
$\nu \in [\ell ]$ such that  $\sigma (\nu -1)\leq \mu -1<\sigma (\nu )$;
$\sigma (\nu -1)\leq \mu -1<\sigma (\nu )$;(3)
 $(\emptyset, \sigma ^*\beta ;\emptyset, \emptyset )$ if
$(\emptyset, \sigma ^*\beta ;\emptyset, \emptyset )$ if  $\sigma (0)\geq \mu$.
$\sigma (0)\geq \mu$.
Similarly, we can describe ![]() $\mathrm {Seq}_k(N(\mathrm {Fin}_*){\bigcirc{\kern-6pt \star}}[1])$: an object is a four-tuple
$\mathrm {Seq}_k(N(\mathrm {Fin}_*){\bigcirc{\kern-6pt \star}}[1])$: an object is a four-tuple ![]() $(\alpha,\beta ; \tau _0,\tau _1)$, represented by the diagram
$(\alpha,\beta ; \tau _0,\tau _1)$, represented by the diagram

and a morphism from ![]() $(\alpha,\beta ;\tau _0,\tau _1)$ to
$(\alpha,\beta ;\tau _0,\tau _1)$ to ![]() $(\alpha,\beta ;\tau _0',\tau _1')$ corresponds to a morphism
$(\alpha,\beta ;\tau _0',\tau _1')$ corresponds to a morphism ![]() $\varphi : \langle \xi '\rangle \rightarrow \langle \xi \rangle$ in
$\varphi : \langle \xi '\rangle \rightarrow \langle \xi \rangle$ in ![]() $\mathrm {Fin}_*$ such that the following diagram commutes.
$\mathrm {Fin}_*$ such that the following diagram commutes.

For any map ![]() $\sigma : [\ell ]\rightarrow [k]$, the functor
$\sigma : [\ell ]\rightarrow [k]$, the functor ![]() $\sigma ^*: \mathrm {Seq}_k(N(\mathrm {Fin}_*){\bigcirc{\kern-6pt \star}}[1])\rightarrow \mathrm {Seq}_\ell (N(\mathrm {Fin}_*){\bigcirc{\kern-6pt \star}}[1])$ is similar as above.
$\sigma ^*: \mathrm {Seq}_k(N(\mathrm {Fin}_*){\bigcirc{\kern-6pt \star}}[1])\rightarrow \mathrm {Seq}_\ell (N(\mathrm {Fin}_*){\bigcirc{\kern-6pt \star}}[1])$ is similar as above.
Let ![]() $\pi _{{\bigcirc{\kern-6pt \star}}}: I_{N(\Delta )^{\textrm {op}}{\bigcirc{\kern-6pt \star}}[1]}\rightarrow N(\Delta )^{\textrm {op}}$ (respectively,
$\pi _{{\bigcirc{\kern-6pt \star}}}: I_{N(\Delta )^{\textrm {op}}{\bigcirc{\kern-6pt \star}}[1]}\rightarrow N(\Delta )^{\textrm {op}}$ (respectively, ![]() $\pi _{{\bigcirc{\kern-6pt \star}}}^\mathrm {Comm}: I^\mathrm {Comm}_{N(\Delta )^{\textrm {op}}{\bigcirc{\kern-6pt \star}}[1]}\rightarrow N(\Delta )^{\textrm {op}}$) be the coCartesian fibration from the Grothendieck construction for
$\pi _{{\bigcirc{\kern-6pt \star}}}^\mathrm {Comm}: I^\mathrm {Comm}_{N(\Delta )^{\textrm {op}}{\bigcirc{\kern-6pt \star}}[1]}\rightarrow N(\Delta )^{\textrm {op}}$) be the coCartesian fibration from the Grothendieck construction for ![]() $\mathrm {Seq}_\bullet (N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1]): N(\Delta )^{\textrm {op}}\rightarrow 1\textrm {-}\mathcal {C}\mathrm {at}^\mathrm {ord}$ (respectively,
$\mathrm {Seq}_\bullet (N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1]): N(\Delta )^{\textrm {op}}\rightarrow 1\textrm {-}\mathcal {C}\mathrm {at}^\mathrm {ord}$ (respectively, ![]() $\mathrm {Seq}_\bullet (\mathrm {Fin}_*{\bigcirc{\kern-6pt \star}}[1]): N(\Delta )^{\textrm {op}}\rightarrow 1\textrm {-}\mathcal {C}\mathrm {at}^\mathrm {ord}$), where
$\mathrm {Seq}_\bullet (\mathrm {Fin}_*{\bigcirc{\kern-6pt \star}}[1]): N(\Delta )^{\textrm {op}}\rightarrow 1\textrm {-}\mathcal {C}\mathrm {at}^\mathrm {ord}$), where ![]() $1\text {-}\mathcal {C}\mathrm {at}^\mathrm {ord}$ means the full subcategory of
$1\text {-}\mathcal {C}\mathrm {at}^\mathrm {ord}$ means the full subcategory of ![]() $1\text {-}\mathcal {C}\mathrm {at}$ consisting of ordinary 1-categories. We introduce another coCartesian fibration
$1\text {-}\mathcal {C}\mathrm {at}$ consisting of ordinary 1-categories. We introduce another coCartesian fibration ![]() $\pi _{I_+}: I_+\rightarrow N(\Delta )^{\rm op}$, which is the Grothendieck construction of the functor
$\pi _{I_+}: I_+\rightarrow N(\Delta )^{\rm op}$, which is the Grothendieck construction of the functor
 \begin{align*} & N(\Delta)^{\rm op}\rightarrow \mathrm{Sets}\\ &[n]\mapsto \{(s,e)|s: \Delta^n\rightarrow N(\Delta)^{\rm op}, e\in\{-1,0,\ldots, n\}\}\\ &([n]\leftarrow [m]:\alpha^{\rm op})\mapsto (f: (s,e)\mapsto ((\alpha^{\rm op})^*s, e'=\begin{cases}-1,\text{ if }\alpha^{\rm op}(0)>e;\\ m, \text{ if }\alpha^{\rm op}(n)< e+1;\\ \text{the unique element }u \text{ such that }\\ \ \ [e,e+1]\subset\alpha^{\rm op}([u,u+1]), \text{ otherwise} \end{cases})). \end{align*}
\begin{align*} & N(\Delta)^{\rm op}\rightarrow \mathrm{Sets}\\ &[n]\mapsto \{(s,e)|s: \Delta^n\rightarrow N(\Delta)^{\rm op}, e\in\{-1,0,\ldots, n\}\}\\ &([n]\leftarrow [m]:\alpha^{\rm op})\mapsto (f: (s,e)\mapsto ((\alpha^{\rm op})^*s, e'=\begin{cases}-1,\text{ if }\alpha^{\rm op}(0)>e;\\ m, \text{ if }\alpha^{\rm op}(n)< e+1;\\ \text{the unique element }u \text{ such that }\\ \ \ [e,e+1]\subset\alpha^{\rm op}([u,u+1]), \text{ otherwise} \end{cases})). \end{align*}
Here we think of ![]() $e$ as a marked edge
$e$ as a marked edge ![]() $\{i,i+1\}$ in
$\{i,i+1\}$ in ![]() $\Delta ^n$ when
$\Delta ^n$ when ![]() $i\in [0,n-1]$, and when
$i\in [0,n-1]$, and when ![]() $i=-1, n$, we get a degenerate marked edge at
$i=-1, n$, we get a degenerate marked edge at ![]() $0$ and
$0$ and ![]() $n$ respectively. In a similar way, we can define
$n$ respectively. In a similar way, we can define ![]() $\pi _{I_+}^{\mathrm {Comm}}: I_+^\mathrm {Comm}\rightarrow N(\Delta )^{\rm op}$.
$\pi _{I_+}^{\mathrm {Comm}}: I_+^\mathrm {Comm}\rightarrow N(\Delta )^{\rm op}$.
Lemma 2.11 The natural functors
and
 \begin{align*} \pi_{{\bigcirc{\kern-6pt \star}}, I_+}^\mathrm{Comm}: I_{N(\mathrm{Fin}_*){\bigcirc{\kern-6pt \star}}[1]}&\longrightarrow I_+^\mathrm{Comm}\\ (\alpha,\beta; \tau_0,\tau_1)&\mapsto ((\alpha,\tau_1\tau_0,\beta), e=\mu-1), \end{align*}
\begin{align*} \pi_{{\bigcirc{\kern-6pt \star}}, I_+}^\mathrm{Comm}: I_{N(\mathrm{Fin}_*){\bigcirc{\kern-6pt \star}}[1]}&\longrightarrow I_+^\mathrm{Comm}\\ (\alpha,\beta; \tau_0,\tau_1)&\mapsto ((\alpha,\tau_1\tau_0,\beta), e=\mu-1), \end{align*}
are coCartesian fibrations.
Proof. By construction, every edge in ![]() $I_+$ is
$I_+$ is ![]() $\pi _{I_+}$-coCartesian. By [Reference LurieLur09, Proposition 2.4.1.3], every
$\pi _{I_+}$-coCartesian. By [Reference LurieLur09, Proposition 2.4.1.3], every ![]() $\pi _{{\bigcirc{\kern-6pt \star}}}$-coCartesian edge in
$\pi _{{\bigcirc{\kern-6pt \star}}}$-coCartesian edge in ![]() $I_{N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1]}$ is also
$I_{N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1]}$ is also ![]() $\pi _{{\bigcirc{\kern-6pt \star}}, I_+}$-coCartesian. Since
$\pi _{{\bigcirc{\kern-6pt \star}}, I_+}$-coCartesian. Since ![]() $\pi _{{\bigcirc{\kern-6pt \star}}}$ is a coCartesian fibration, the claim for
$\pi _{{\bigcirc{\kern-6pt \star}}}$ is a coCartesian fibration, the claim for ![]() $\pi _{{\bigcirc{\kern-6pt \star}},I_+}$ follows. The part for
$\pi _{{\bigcirc{\kern-6pt \star}},I_+}$ follows. The part for ![]() $\pi _{{\bigcirc{\kern-6pt \star}},I_+}^\mathrm {Comm}$ follows similarly.
$\pi _{{\bigcirc{\kern-6pt \star}},I_+}^\mathrm {Comm}$ follows similarly.
Lemma 2.12 For any ![]() $\infty$-category
$\infty$-category ![]() $S$, a coCartesian fibration
$S$, a coCartesian fibration ![]() $X\rightarrow S$, a Cartesian fibration
$X\rightarrow S$, a Cartesian fibration ![]() $Y\rightarrow S$ and an ordinary 1-category
$Y\rightarrow S$ and an ordinary 1-category ![]() $\mathcal {C}$, to give a functor
$\mathcal {C}$, to give a functor ![]() $F: X\times _S Y\rightarrow \mathcal {C}$, it suffices to give the following data:
$F: X\times _S Y\rightarrow \mathcal {C}$, it suffices to give the following data:
(a) a functor
 $F_s: X_s\times Y_s\rightarrow \mathcal {C}$ for each fiber over
$F_s: X_s\times Y_s\rightarrow \mathcal {C}$ for each fiber over  $s\in S$;
$s\in S$;(b) for each edge
 $(\alpha,\beta ): (x_0,y_0)\rightarrow (x_1,y_1)$ in
$(\alpha,\beta ): (x_0,y_0)\rightarrow (x_1,y_1)$ in  $X\times _SY$ over an edge
$X\times _SY$ over an edge  $p(\alpha ): s\rightarrow t$ in
$p(\alpha ): s\rightarrow t$ in  $S$, given by a coCartesian edge
$S$, given by a coCartesian edge  $(\alpha : x_0\rightarrow x_1)$ and a Cartesian edge
$(\alpha : x_0\rightarrow x_1)$ and a Cartesian edge  $(\beta : y_0\rightarrow y_1)$ over
$(\beta : y_0\rightarrow y_1)$ over  $p(\alpha )$, a morphism in
$p(\alpha )$, a morphism in  $\mathcal {C}$ from
$\mathcal {C}$ from  $F_s(x_0,y_0)$ to
$F_s(x_0,y_0)$ to  $F_t(x_1,y_1)$, such that for any commutative diagrams in
$F_t(x_1,y_1)$, such that for any commutative diagrams in  $X,Y$, respectively,
where the horizontal arrows are coCartesian/Cartesian, respectively, and the left (respectively, right) vertical arrow in each diagram is in
$X,Y$, respectively,
where the horizontal arrows are coCartesian/Cartesian, respectively, and the left (respectively, right) vertical arrow in each diagram is in
 $X_s, Y_s$ (respectively,
$X_s, Y_s$ (respectively,  $X_t, Y_t$) respectively, the following diagram commutes in
$X_t, Y_t$) respectively, the following diagram commutes in  $\mathcal {C}$.
(2.4.1)
$\mathcal {C}$.
(2.4.1)
(c) The assignment in part (b) is compatible with composition of coCartesian and Cartesian edges in
 $X$ and
$X$ and  $Y$, respectively.
$Y$, respectively.
Proof. Any morphism ![]() $f:(x_0,y_0)\rightarrow (x_1,y_1)$ over
$f:(x_0,y_0)\rightarrow (x_1,y_1)$ over ![]() $s\rightarrow t$ in
$s\rightarrow t$ in ![]() $S$ factors uniquely as
$S$ factors uniquely as

where the vertical arrows are contained in ![]() $X_s\times Y_s$ and
$X_s\times Y_s$ and ![]() $X_t\times Y_t$, respectively, and the horizontal arrow
$X_t\times Y_t$, respectively, and the horizontal arrow ![]() $(\alpha,\beta )$ has
$(\alpha,\beta )$ has ![]() $\alpha$ (respectively,
$\alpha$ (respectively, ![]() $\beta$) a coCartesian (respectively, Cartesian) arrow. Now if, in addition, we have
$\beta$) a coCartesian (respectively, Cartesian) arrow. Now if, in addition, we have ![]() $g: (x_1,y_1)\rightarrow (x_2,y_2)$ over
$g: (x_1,y_1)\rightarrow (x_2,y_2)$ over ![]() $t\rightarrow u$ in
$t\rightarrow u$ in ![]() $S$ and
$S$ and ![]() $g\circ f$ factor as follows
$g\circ f$ factor as follows

then we have a commutative diagram

in which the arrows ![]() $\beta _{012}$ (respectively,
$\beta _{012}$ (respectively, ![]() $\alpha _{012}$) is Cartesian (respectively, coCartesian), and
$\alpha _{012}$) is Cartesian (respectively, coCartesian), and ![]() $\gamma _{12}$ (respectively,
$\gamma _{12}$ (respectively, ![]() $\eta _{01}$) is the image under pullback (respectively, pushforward) along the Cartesian (respectively, coCartesian) arrows from
$\eta _{01}$) is the image under pullback (respectively, pushforward) along the Cartesian (respectively, coCartesian) arrows from ![]() $F_s\rightarrow F_t$ (respectively,
$F_s\rightarrow F_t$ (respectively, ![]() $F_t\rightarrow F_u$). Therefore, to define a functor
$F_t\rightarrow F_u$). Therefore, to define a functor ![]() $X\times _S Y\rightarrow \mathcal {C}$, we just need to define functor
$X\times _S Y\rightarrow \mathcal {C}$, we just need to define functor ![]() $F_s: X_s\times Y_s\rightarrow \mathcal {C}$ for every
$F_s: X_s\times Y_s\rightarrow \mathcal {C}$ for every ![]() $s\in S$, and a morphism
$s\in S$, and a morphism ![]() $F_s(x_0,y_0)\rightarrow F_t(x_1,y_1)$ for each edge
$F_s(x_0,y_0)\rightarrow F_t(x_1,y_1)$ for each edge ![]() $(\alpha _{01},\beta _{01})$ as above, so that diagram (
$(\alpha _{01},\beta _{01})$ as above, so that diagram (
) is sent to a commutative diagram in ![]() $\mathcal {C}$. It is easy to see that these are exactly the data (a), (b), and (c) in the lemma.
$\mathcal {C}$. It is easy to see that these are exactly the data (a), (b), and (c) in the lemma.
By [Reference Gaitsgory and RozenblyumGR17, Chapters 9, 1.4.5 and 10, 3.2.7], to give a right-lax homomorphism between two associative (respectively, commutative) algebra objects in ![]() $\mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}$ (respectively,
$\mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}$ (respectively, ![]() $\mathbf {Corr}(\mathcal {C})^{\otimes, \mathrm {Fin}_*}$) is the same as to construct a functor from
$\mathbf {Corr}(\mathcal {C})^{\otimes, \mathrm {Fin}_*}$) is the same as to construct a functor from ![]() $N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1]$ (respectively,
$N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1]$ (respectively, ![]() $N(\mathrm {Fin}_*){\bigcirc{\kern-6pt \star}}[1]$) to
$N(\mathrm {Fin}_*){\bigcirc{\kern-6pt \star}}[1]$) to ![]() $\mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}$ (respectively,
$\mathbf {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}$ (respectively, ![]() $\mathbf {Corr}(\mathcal {C})^{\otimes, \mathrm {Fin}_*}$) over
$\mathbf {Corr}(\mathcal {C})^{\otimes, \mathrm {Fin}_*}$) over ![]() $N(\Delta )^{\rm op}$ (respectively,
$N(\Delta )^{\rm op}$ (respectively, ![]() $N(\mathrm {Fin}_*)$), such that the restriction of the functor to
$N(\mathrm {Fin}_*)$), such that the restriction of the functor to ![]() $N(\Delta )^{\rm op}\times \{\epsilon \}$ (respectively,
$N(\Delta )^{\rm op}\times \{\epsilon \}$ (respectively, ![]() $N(\mathrm {Fin}_*)\times \{\epsilon \}$),
$N(\mathrm {Fin}_*)\times \{\epsilon \}$), ![]() $\epsilon =0,1$ coincides with the two associative (respectively, commutative) algebra objects respectively (up to homotopy). Therefore, we are aiming to define for each
$\epsilon =0,1$ coincides with the two associative (respectively, commutative) algebra objects respectively (up to homotopy). Therefore, we are aiming to define for each ![]() $(\alpha,\beta ;\tau _0,\tau _1)\in \mathrm {Seq}_k(N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1])$ (respectively,
$(\alpha,\beta ;\tau _0,\tau _1)\in \mathrm {Seq}_k(N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1])$ (respectively, ![]() $(\alpha,\beta ;\tau _0,\tau _1)\in \mathrm {Seq}_k(N(\mathrm {Fin}_*){\bigcirc{\kern-6pt \star}}[1])$) a diagram
$(\alpha,\beta ;\tau _0,\tau _1)\in \mathrm {Seq}_k(N(\mathrm {Fin}_*){\bigcirc{\kern-6pt \star}}[1])$) a diagram ![]() $W_{\alpha,\beta ;\tau _0,\tau _1}$ in
$W_{\alpha,\beta ;\tau _0,\tau _1}$ in ![]() $\mathrm {Fun}''(([k]\times [k]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\otimes,\Delta })$ (respectively,
$\mathrm {Fun}''(([k]\times [k]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\otimes,\Delta })$ (respectively, ![]() $\mathrm {Fun}''(([k]\times [k]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\otimes,(\mathrm {Fin}_*)^{\rm op}})$) satisfying required properties.
$\mathrm {Fun}''(([k]\times [k]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C}^{\otimes,(\mathrm {Fin}_*)^{\rm op}})$) satisfying required properties.
By the approach in § 2.3, we just need to construct an element in  $\mathrm {Hom}_{I}(I^\natural _{N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1]}\underset {I}{\times }\mathcal {T}^\natural, (\mathcal {C}\times I)^\natural )$ (respectively,
$\mathrm {Hom}_{I}(I^\natural _{N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1]}\underset {I}{\times }\mathcal {T}^\natural, (\mathcal {C}\times I)^\natural )$ (respectively, ![]() $\mathrm {Hom}_{I}(I^\natural _{N(\mathrm {Fin}_*){\bigcirc{\kern-6pt \star}}[1]}\underset {I}{\times } \mathcal {T}^\natural, (\mathcal {C}\times I)^\natural )$). For this purpose, we first define a Cartesian fibration
$\mathrm {Hom}_{I}(I^\natural _{N(\mathrm {Fin}_*){\bigcirc{\kern-6pt \star}}[1]}\underset {I}{\times } \mathcal {T}^\natural, (\mathcal {C}\times I)^\natural )$). For this purpose, we first define a Cartesian fibration ![]() $\pi _{\mathcal {T}_+}:\mathcal {T}_+\rightarrow I_+$ which can be thought of as an extension of
$\pi _{\mathcal {T}_+}:\mathcal {T}_+\rightarrow I_+$ which can be thought of as an extension of ![]() $\pi _{\mathcal {T}}: \mathcal {T}\rightarrow I$. Consider the ordinary 1-category
$\pi _{\mathcal {T}}: \mathcal {T}\rightarrow I$. Consider the ordinary 1-category
 \begin{align*}
\Gamma_{[n],e}&:=([0,e]\times [0,n]^{\rm op})^{\geq
\mathrm{dgnl}})\times\{0\}_1 \coprod_{[0,e]\times
[e+1,n]^{\rm op}\times \{0\}_1}
\bigg([0,e]\times[e+1,n]^{\rm op}\times
\bigg(\Delta^1_1\coprod_{\Delta^{\{1\}}}\Delta^1_2\bigg)\bigg)\\
&\quad\ \, \coprod_{[0,e]\times [e+1,n]^{\rm
op}\times \{0\}_2}([0,n]\times [e+1,n]^{\rm op})\times
\{0\}_2, \end{align*}
\begin{align*}
\Gamma_{[n],e}&:=([0,e]\times [0,n]^{\rm op})^{\geq
\mathrm{dgnl}})\times\{0\}_1 \coprod_{[0,e]\times
[e+1,n]^{\rm op}\times \{0\}_1}
\bigg([0,e]\times[e+1,n]^{\rm op}\times
\bigg(\Delta^1_1\coprod_{\Delta^{\{1\}}}\Delta^1_2\bigg)\bigg)\\
&\quad\ \, \coprod_{[0,e]\times [e+1,n]^{\rm
op}\times \{0\}_2}([0,n]\times [e+1,n]^{\rm op})\times
\{0\}_2, \end{align*}
which has a natural functor to ![]() $[n]^{\rm op}$ from projecting to the second factor (see Figure 1). The functor
$[n]^{\rm op}$ from projecting to the second factor (see Figure 1). The functor ![]() $\pi _{\mathcal {T}_+}$ comes from the Grothendieck construction of the following functor
$\pi _{\mathcal {T}_+}$ comes from the Grothendieck construction of the following functor
 \begin{align*} & f_{I_+}: I_+^{\rm op}\longrightarrow1\text{-}\mathcal{C}\mathrm{at}^\mathrm{ord}\\ &([n], (s,e))\mapsto \Gamma_{[n],e}\underset{N(\Delta)}{\times}T, \end{align*}
\begin{align*} & f_{I_+}: I_+^{\rm op}\longrightarrow1\text{-}\mathcal{C}\mathrm{at}^\mathrm{ord}\\ &([n], (s,e))\mapsto \Gamma_{[n],e}\underset{N(\Delta)}{\times}T, \end{align*}
for any morphism ![]() $([m], ((\alpha ^{\rm op})^*s,e'))\rightarrow ([n],(s,e))$ in
$([m], ((\alpha ^{\rm op})^*s,e'))\rightarrow ([n],(s,e))$ in ![]() $I_+^{\rm op}$ induced by
$I_+^{\rm op}$ induced by ![]() $\alpha ^{\rm op}: [m]\rightarrow [n]$ in
$\alpha ^{\rm op}: [m]\rightarrow [n]$ in ![]() $N(\Delta )$, the corresponding morphism under
$N(\Delta )$, the corresponding morphism under ![]() $f_{I_+}$ is the natural one that sends
$f_{I_+}$ is the natural one that sends ![]() $(i,j,\eta ; u\leq u+1)\in [m]\times [m]^{\rm op}\times \{\{0\}_1,\{0\}_2,\{1\}\}$ to
$(i,j,\eta ; u\leq u+1)\in [m]\times [m]^{\rm op}\times \{\{0\}_1,\{0\}_2,\{1\}\}$ to ![]() $(\alpha ^{\rm op}(i), \alpha ^{\rm op}(j), \eta ; u\leq u+1)$.
$(\alpha ^{\rm op}(i), \alpha ^{\rm op}(j), \eta ; u\leq u+1)$.

Figure 1. A picture of ![]() $\Gamma _{[n],s,e}$.
$\Gamma _{[n],s,e}$.
2.4.1 Construction of the main functor
Now we define a functor from ![]() $F_{{\bigcirc{\kern-6pt \star}},\mathcal {T}_+}: I_{N(\Delta )^{\textrm {op}}{\bigcirc{\kern-6pt \star}}[1]}\underset {I_+}{\times }\mathcal {T}_+\rightarrow N(\Delta )^{\textrm {op}}\times (\Delta ^{\{W,C\}}\coprod _{\Delta ^{\{W\}}}\Delta ^{\{W,D\}})$ as follows. First, on the object level, we have
$F_{{\bigcirc{\kern-6pt \star}},\mathcal {T}_+}: I_{N(\Delta )^{\textrm {op}}{\bigcirc{\kern-6pt \star}}[1]}\underset {I_+}{\times }\mathcal {T}_+\rightarrow N(\Delta )^{\textrm {op}}\times (\Delta ^{\{W,C\}}\coprod _{\Delta ^{\{W\}}}\Delta ^{\{W,D\}})$ as follows. First, on the object level, we have
 \begin{align}
& F_{{\bigcirc{\kern-6pt \star}},\mathcal{T}_+}:
I_{N(\Delta)^{\rm
op}{\bigcirc{\kern-6pt \star}}[1]}\underset{I_+}{\times}\mathcal{T}_+\rightarrow
N(\Delta)^{\rm op}\times
\bigg(\Delta^{\{W,C\}}\coprod_{\Delta^{\{W\}}}\Delta^{\{W,D\}}\bigg)\\
&(\alpha, \beta,\tau_0,\tau_1;[n], (s,e); i,j,\{0\}_1;u\leq
u+1)\mapsto ([\alpha_{ji}(u),\alpha_{ji}(u+1)], \{C\}),\quad
\text{ if }i\leq j\leq e;\nonumber\\ &(\alpha,
\beta,\tau_0,\tau_1;[n], (s,e); i,e+1+j,\{0\}_1;u\leq
u+1)\nonumber\\ &\quad\mapsto ([\alpha_{ei}\tau_0\tau_1\beta_{j0}(u),
\alpha_{ei}\tau_0\tau_1\beta_{j0}(u+1)], \{C\}),\quad i\leq e,
j\geq 0;\nonumber\\ &(\alpha, \beta,\tau_0,\tau_1;[n],
(s,e); i,e+1+j,\{1\};u\leq u+1)\nonumber\\ &\quad \mapsto
([\tau_1\beta_{j0}(u),\tau_1\beta_{j0}(u+1)], \{C\}), \quad i\leq
e, j\geq 0;\nonumber\\ &(\alpha, \beta,\tau_0,\tau_1;[n],
(s,e); i,e+1+j,\{0\}_2;u\leq u+1)\nonumber\\ &\quad \mapsto
([\tau_1\beta_{j0}(u),\tau_1\beta_{j0}(u+1)], \{W\}),\quad i\leq
e, j\geq 0;\nonumber\\ &(\alpha, \beta,\tau_0,\tau_1;[n],
(s,e);e+1+i,e+1+j,\{0\}_2; u\leq u+1)\nonumber\\ &\quad \mapsto
([\beta_{ji}(u),\beta_{ji}(u+1)], \{D\}), \quad \text{ if }0\leq
i\leq j. \nonumber
\end{align}
\begin{align}
& F_{{\bigcirc{\kern-6pt \star}},\mathcal{T}_+}:
I_{N(\Delta)^{\rm
op}{\bigcirc{\kern-6pt \star}}[1]}\underset{I_+}{\times}\mathcal{T}_+\rightarrow
N(\Delta)^{\rm op}\times
\bigg(\Delta^{\{W,C\}}\coprod_{\Delta^{\{W\}}}\Delta^{\{W,D\}}\bigg)\\
&(\alpha, \beta,\tau_0,\tau_1;[n], (s,e); i,j,\{0\}_1;u\leq
u+1)\mapsto ([\alpha_{ji}(u),\alpha_{ji}(u+1)], \{C\}),\quad
\text{ if }i\leq j\leq e;\nonumber\\ &(\alpha,
\beta,\tau_0,\tau_1;[n], (s,e); i,e+1+j,\{0\}_1;u\leq
u+1)\nonumber\\ &\quad\mapsto ([\alpha_{ei}\tau_0\tau_1\beta_{j0}(u),
\alpha_{ei}\tau_0\tau_1\beta_{j0}(u+1)], \{C\}),\quad i\leq e,
j\geq 0;\nonumber\\ &(\alpha, \beta,\tau_0,\tau_1;[n],
(s,e); i,e+1+j,\{1\};u\leq u+1)\nonumber\\ &\quad \mapsto
([\tau_1\beta_{j0}(u),\tau_1\beta_{j0}(u+1)], \{C\}), \quad i\leq
e, j\geq 0;\nonumber\\ &(\alpha, \beta,\tau_0,\tau_1;[n],
(s,e); i,e+1+j,\{0\}_2;u\leq u+1)\nonumber\\ &\quad \mapsto
([\tau_1\beta_{j0}(u),\tau_1\beta_{j0}(u+1)], \{W\}),\quad i\leq
e, j\geq 0;\nonumber\\ &(\alpha, \beta,\tau_0,\tau_1;[n],
(s,e);e+1+i,e+1+j,\{0\}_2; u\leq u+1)\nonumber\\ &\quad \mapsto
([\beta_{ji}(u),\beta_{ji}(u+1)], \{D\}), \quad \text{ if }0\leq
i\leq j. \nonumber
\end{align}
By Lemma 2.12, to give a complete definition of ![]() $F_{{\bigcirc{\kern-6pt \star}}, \mathcal {T}_+}$, we just need to give the following data.
$F_{{\bigcirc{\kern-6pt \star}}, \mathcal {T}_+}$, we just need to give the following data.
(a) For any ![]() $([n], (s,e))\in I_+$,
$([n], (s,e))\in I_+$,
 \begin{equation} F_{{\bigcirc{\kern-6pt \star}},\mathcal{T}_+; [n],(s,e)}: (I_{N(\Delta)^{\rm op}{\bigcirc{\kern-6pt \star}}[1]})_{[n],(s,e)}\rightarrow \mathrm{Fun}\bigg((\mathcal{T}_+)_{[n],(s,e)}, N(\Delta)^{\rm op}\times \bigg(\Delta^{\{W,C\}}\coprod_{\Delta^{\{W\}}}\Delta^{\{W,D\}}\bigg)\bigg). \end{equation}
\begin{equation} F_{{\bigcirc{\kern-6pt \star}},\mathcal{T}_+; [n],(s,e)}: (I_{N(\Delta)^{\rm op}{\bigcirc{\kern-6pt \star}}[1]})_{[n],(s,e)}\rightarrow \mathrm{Fun}\bigg((\mathcal{T}_+)_{[n],(s,e)}, N(\Delta)^{\rm op}\times \bigg(\Delta^{\{W,C\}}\coprod_{\Delta^{\{W\}}}\Delta^{\{W,D\}}\bigg)\bigg). \end{equation} Let ![]() $[0,n]_{e,+}$ be the ordered set
$[0,n]_{e,+}$ be the ordered set ![]() $[0,n]\sqcup \{e_+\}$ with
$[0,n]\sqcup \{e_+\}$ with ![]() $e< e_+< e+1$. Consider the ordinary 1-category
$e< e_+< e+1$. Consider the ordinary 1-category
 \begin{align*}
S_{[n],e_+}&=(([0,n]_{e,+}\times [0,n]^{\rm op})^{\geq
\mathrm{dgnl}}\times \{0\}_1)\\ &\quad \:\coprod_{([e_+, n]\times
[e+1,n]^{\rm op})^{\geq
\mathrm{dgnl}}\times \{0\}_1} (([e_+, n]\times
[e+1,n]^{\rm op})^{\geq \mathrm{dgnl}}\times
\Delta^{\{\{0\}_2,\{0\}_1\}}), \end{align*}
\begin{align*}
S_{[n],e_+}&=(([0,n]_{e,+}\times [0,n]^{\rm op})^{\geq
\mathrm{dgnl}}\times \{0\}_1)\\ &\quad \:\coprod_{([e_+, n]\times
[e+1,n]^{\rm op})^{\geq
\mathrm{dgnl}}\times \{0\}_1} (([e_+, n]\times
[e+1,n]^{\rm op})^{\geq \mathrm{dgnl}}\times
\Delta^{\{\{0\}_2,\{0\}_1\}}), \end{align*}
which has a natural functor to ![]() $[n]^{\rm op}$ by projecting to the second factor (see Figure 2). There is a unique functor
$[n]^{\rm op}$ by projecting to the second factor (see Figure 2). There is a unique functor
that:
(i) collapses the vertical edges
 $(i,j,\eta )\rightarrow (i+1, j,\eta )$ to the identity morphism at
$(i,j,\eta )\rightarrow (i+1, j,\eta )$ to the identity morphism at  $(e_+, j,\eta )$ for
$(e_+, j,\eta )$ for  $i< e, j\geq e+1,\eta \in \{\{1\},\{0\}_2\}$;
$i< e, j\geq e+1,\eta \in \{\{1\},\{0\}_2\}$;(ii) is the identity on the subcategories
 $(([0,e]\times [0,n]^{\rm op})^{\geq \mathrm {dgnl}}\times \{0\}_1)$ and restricts to an equivalence of subcategories
$(([0,e]\times [0,n]^{\rm op})^{\geq \mathrm {dgnl}}\times \{0\}_1)$ and restricts to an equivalence of subcategories
 \begin{align*} &([e,n]\times [e+1,n]^{\rm op})^{\geq \mathrm{dgnl}}\times \{0\}_2\overset{\sim}{\rightarrow} ([e_+, n]\times [e+1,n]^{\rm op})^{\geq\mathrm{dgnl}}\times\{0\}_2\\ &\{e\}\times [e+1,n]^{\rm op}\times\Delta_2^1\overset{\sim}{\rightarrow} \{e_+\}\times[e+1,n]^{\rm op}\times \Delta_2^1; \end{align*}
\begin{align*} &([e,n]\times [e+1,n]^{\rm op})^{\geq \mathrm{dgnl}}\times \{0\}_2\overset{\sim}{\rightarrow} ([e_+, n]\times [e+1,n]^{\rm op})^{\geq\mathrm{dgnl}}\times\{0\}_2\\ &\{e\}\times [e+1,n]^{\rm op}\times\Delta_2^1\overset{\sim}{\rightarrow} \{e_+\}\times[e+1,n]^{\rm op}\times \Delta_2^1; \end{align*}
(iii) restricts to an equivalence of subcategories
 \[ \{e\}\times [e+1,n]^{\rm op}\times\Delta_1^{1}\overset{\sim}{\rightarrow} [e,e_+]\times [e+1,n]^{\rm op}\times\{0\}_1. \]
\[ \{e\}\times [e+1,n]^{\rm op}\times\Delta_1^{1}\overset{\sim}{\rightarrow} [e,e_+]\times [e+1,n]^{\rm op}\times\{0\}_1. \]
Property (ii) (respectively, property (iii)) is illustrated by the white wall at the back and gray faces (respectively, the faces hatched by lines) in both Figures 1 and 2.

Figure 2. A picture of ![]() $S_{[n],e_+}$.
$S_{[n],e_+}$.
For any ![]() $([n],s,e)\in I_+$, let
$([n],s,e)\in I_+$, let
be the functor induced from ![]() $\widetilde {C}_e$.
$\widetilde {C}_e$.
Given any ![]() $s^\tau =(\alpha,\beta,\tau _0,\tau _1)\in (I_{N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1]})_{[n],(s,e)}$ which we will also think of as a functor
$s^\tau =(\alpha,\beta,\tau _0,\tau _1)\in (I_{N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1]})_{[n],(s,e)}$ which we will also think of as a functor ![]() $[n]_{e,+}\rightarrow N(\Delta )^{\rm op}$, let
$[n]_{e,+}\rightarrow N(\Delta )^{\rm op}$, let
 \[ F_{2,\tau}: S_{[n],e_+}\underset{N(\Delta)}{\times }T\rightarrow N(\Delta)^{\rm op}\times \bigg(\Delta^{\{W, C\}}\coprod_{\Delta^{\{W\}}}\Delta^{\{W,D\}}\bigg) \]
\[ F_{2,\tau}: S_{[n],e_+}\underset{N(\Delta)}{\times }T\rightarrow N(\Delta)^{\rm op}\times \bigg(\Delta^{\{W, C\}}\coprod_{\Delta^{\{W\}}}\Delta^{\{W,D\}}\bigg) \]
be the functor given by the product of ![]() $G_{1,\tau }\circ \mathrm {proj}$ and
$G_{1,\tau }\circ \mathrm {proj}$ and ![]() $G_2\circ \mathrm {proj}$ defined as follows:
$G_2\circ \mathrm {proj}$ defined as follows:
where ![]() $G_{1,\tau}$ is defined similarly as
$G_{1,\tau}$ is defined similarly as ![]() $F_{\mathcal{T},\Delta^{\rm op}}$ that is induced by
$F_{\mathcal{T},\Delta^{\rm op}}$ that is induced by ![]() $s^\tau$ and
$s^\tau$ and ![]() $G_2$ is the one sending
$G_2$ is the one sending ![]() $(i,j,\{0\}_1)$ to C,
$(i,j,\{0\}_1)$ to C, ![]() $(e_+,j,\{0\}_2)$ to W, and
$(e_+,j,\{0\}_2)$ to W, and ![]() $(e+i,j,\{0\}_2)$ to D for
$(e+i,j,\{0\}_2)$ to D for ![]() $i>0$.
$i>0$.
Now for each ![]() $([n], s^\tau )\in (I_{N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1]})_{[n],(s,e)}$, where
$([n], s^\tau )\in (I_{N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1]})_{[n],(s,e)}$, where ![]() $s^\tau =(\alpha,\beta,\tau _0,\tau _1)$ as above, we define
$s^\tau =(\alpha,\beta,\tau _0,\tau _1)$ as above, we define
(as in (2.4.4)). For any morphism ![]() $([n],s^\tau )\mapsto ([n], s^{\tau '})$ defined by
$([n],s^\tau )\mapsto ([n], s^{\tau '})$ defined by ![]() $\varphi : [\xi ']\rightarrow [\xi ]$ in
$\varphi : [\xi ']\rightarrow [\xi ]$ in ![]() $N(\Delta )$, let
$N(\Delta )$, let ![]() $[n]_{e,+,+}=[n]_{e,+}\sqcup \{e_+'\}$ with the ordering
$[n]_{e,+,+}=[n]_{e,+}\sqcup \{e_+'\}$ with the ordering ![]() $e_+< e_+'< e+1$, and let
$e_+< e_+'< e+1$, and let ![]() $s^{\tau,\tau '}: [n]_{e,+,+}^{\rm op}\rightarrow N(\Delta )$, such that
$s^{\tau,\tau '}: [n]_{e,+,+}^{\rm op}\rightarrow N(\Delta )$, such that ![]() $s^{\tau,\tau '}|_{[n]_{e,+}^{\rm op}}=(s^\tau )^{\rm op}$,
$s^{\tau,\tau '}|_{[n]_{e,+}^{\rm op}}=(s^\tau )^{\rm op}$, ![]() $s^{\tau,\tau '}(e_+'\rightarrow e_+)=\varphi$ and
$s^{\tau,\tau '}(e_+'\rightarrow e_+)=\varphi$ and ![]() $s^{\tau,\tau '}(e+1\rightarrow e_+')=\tau _1'$. Consider the composition
$s^{\tau,\tau '}(e+1\rightarrow e_+')=\tau _1'$. Consider the composition
 \begin{align}
&\Delta^1\times (\mathcal{T}_+)_{[n], s,e}\overset{(id_{\Delta^1},C_{[n],s,e})}{\longrightarrow}\Delta^1\times
(S_{[n],e_+}{\underset{N(\Delta)}{\times}}T)\overset{p}{\rightarrow}
\Delta^1\times (([0,n]_{e,+}\times [0,n]^{\rm op})^{\geq
\mathrm{dgnl}}{\underset{N(\Delta)}{\times}}T)\nonumber\\
&\overset{C_+}{\rightarrow} ([0,n]_{e,+,+}\times [0,n]^{\rm
op})^{\geq
\mathrm{dgnl}}{\underset{N(\Delta)}{\times}}T\overset{F_{\tau,\tau'}}{\rightarrow
}N(\Delta)^{\rm op}, \end{align}
\begin{align}
&\Delta^1\times (\mathcal{T}_+)_{[n], s,e}\overset{(id_{\Delta^1},C_{[n],s,e})}{\longrightarrow}\Delta^1\times
(S_{[n],e_+}{\underset{N(\Delta)}{\times}}T)\overset{p}{\rightarrow}
\Delta^1\times (([0,n]_{e,+}\times [0,n]^{\rm op})^{\geq
\mathrm{dgnl}}{\underset{N(\Delta)}{\times}}T)\nonumber\\
&\overset{C_+}{\rightarrow} ([0,n]_{e,+,+}\times [0,n]^{\rm
op})^{\geq
\mathrm{dgnl}}{\underset{N(\Delta)}{\times}}T\overset{F_{\tau,\tau'}}{\rightarrow
}N(\Delta)^{\rm op}, \end{align}
where:
(i)
 $p$ is determined by the projection
$p$ is determined by the projection  $S_{[n],e_+}\rightarrow ([0,n]_{e,+}\times [0,n]^{\rm op})^{\geq \mathrm {dgnl}}$;
$S_{[n],e_+}\rightarrow ([0,n]_{e,+}\times [0,n]^{\rm op})^{\geq \mathrm {dgnl}}$;(ii)
 $C_+$ is the contraction determined by sending the arrow
$C_+$ is the contraction determined by sending the arrow  $((0,e_+,j;[u,u+1])\rightarrow (1,e_+,j;[u,u+1]))$ to
$((0,e_+,j;[u,u+1])\rightarrow (1,e_+,j;[u,u+1]))$ to  $((e_+,j;[u,u+1])\rightarrow (e_+',j;[u,u+1]))$, and sending
$((e_+,j;[u,u+1])\rightarrow (e_+',j;[u,u+1]))$, and sending  $(\epsilon, i,j;[u,u+1])$ to
$(\epsilon, i,j;[u,u+1])$ to  $(i,j;[u,u+1])$ for
$(i,j;[u,u+1])$ for  $\epsilon =0,1, i\neq e_+$;
$\epsilon =0,1, i\neq e_+$;(iii)
 $F_{\tau,\tau '}$ is defined similarly as
$F_{\tau,\tau '}$ is defined similarly as  $F_{\mathcal {T},\Delta ^{\rm op}}$ induced by
$F_{\mathcal {T},\Delta ^{\rm op}}$ induced by  $s^{\tau,\tau '}$.
$s^{\tau,\tau '}$.
The composite functor (2.4.5) gives a natural transformation
By the naturality of the definition, it is easy to see that ![]() $T_{\tau ',\tau ''}\circ T_{\tau,\tau '}=T_{\tau,\tau ''}$.
$T_{\tau ',\tau ''}\circ T_{\tau,\tau '}=T_{\tau,\tau ''}$.
(b) Over any edge ![]() $([n], (s,e_1))\rightarrow ([m], (\sigma ^*(s), e_2))$ in
$([n], (s,e_1))\rightarrow ([m], (\sigma ^*(s), e_2))$ in ![]() $I_+$ induced by
$I_+$ induced by ![]() $\sigma : [m]\rightarrow [n]$ in
$\sigma : [m]\rightarrow [n]$ in ![]() $N(\Delta )$, we have any
$N(\Delta )$, we have any ![]() $\pi _{{\bigcirc{\kern-6pt \star}}, I_+}$-coCartesian edge of the form
$\pi _{{\bigcirc{\kern-6pt \star}}, I_+}$-coCartesian edge of the form ![]() $\sigma _1:([n],(\alpha,\beta ;\tau _0,\tau _1))\rightarrow ([m], (\sigma ^*(\alpha,\beta ;\tau _0,\tau _1)))$, and any
$\sigma _1:([n],(\alpha,\beta ;\tau _0,\tau _1))\rightarrow ([m], (\sigma ^*(\alpha,\beta ;\tau _0,\tau _1)))$, and any ![]() $\pi _{\mathcal {T}_+}$-Cartesian edge of the form
$\pi _{\mathcal {T}_+}$-Cartesian edge of the form ![]() $\sigma _2(\sigma (i),\sigma (j),\eta ;[u,u+1])\rightarrow (i,j,\eta ;[u,u+1])$, where
$\sigma _2(\sigma (i),\sigma (j),\eta ;[u,u+1])\rightarrow (i,j,\eta ;[u,u+1])$, where ![]() $\eta \in \{\{0\}_1,\{0\}_2,\{1\}\}$. For any commutative diagrams
$\eta \in \{\{0\}_1,\{0\}_2,\{1\}\}$. For any commutative diagrams

we denote ![]() $\sigma ^*(\alpha,\beta ;\tau _0,\tau _1)$ by
$\sigma ^*(\alpha,\beta ;\tau _0,\tau _1)$ by ![]() $(\widetilde {\alpha },\widetilde {\beta };\widetilde {\tau _0},\widetilde {\tau _1})$ and similarly for
$(\widetilde {\alpha },\widetilde {\beta };\widetilde {\tau _0},\widetilde {\tau _1})$ and similarly for ![]() $\sigma ^*(\alpha,\beta ;\tau '_0,\tau '_1)$. By the commutativity of the diagram
$\sigma ^*(\alpha,\beta ;\tau '_0,\tau '_1)$. By the commutativity of the diagram

we see that we just need to make ![]() $F_{{\bigcirc{\kern-6pt \star}},\mathcal {T}_+}(\sigma _1,\sigma _2)=id$, then the diagrams (2.4.1) are all commutative. Thus, we have finished the definition of
$F_{{\bigcirc{\kern-6pt \star}},\mathcal {T}_+}(\sigma _1,\sigma _2)=id$, then the diagrams (2.4.1) are all commutative. Thus, we have finished the definition of ![]() $F_{{\bigcirc{\kern-6pt \star}}, \mathcal {T}_+}$.
$F_{{\bigcirc{\kern-6pt \star}}, \mathcal {T}_+}$.
Let ![]() $C^\bullet, D^\bullet, W^\bullet$ be simplicial objects in
$C^\bullet, D^\bullet, W^\bullet$ be simplicial objects in ![]() $\mathcal {C}$, and let
$\mathcal {C}$, and let ![]() $D^\bullet \leftarrow W^\bullet \rightarrow C^\bullet$ represent a fixed functor
$D^\bullet \leftarrow W^\bullet \rightarrow C^\bullet$ represent a fixed functor ![]() $S_W\in \mathrm {Fun}(N(\Delta )^{\rm op}\times (\Delta ^{\{W, C\}}\coprod _{\Delta ^{\{W\}}}\Delta ^{\{W,D\}}), \mathcal {C})$ whose restriction to
$S_W\in \mathrm {Fun}(N(\Delta )^{\rm op}\times (\Delta ^{\{W, C\}}\coprod _{\Delta ^{\{W\}}}\Delta ^{\{W,D\}}), \mathcal {C})$ whose restriction to ![]() $N(\Delta )^{\rm op}\times \Delta ^{\{?\}}$ is the simplicial object
$N(\Delta )^{\rm op}\times \Delta ^{\{?\}}$ is the simplicial object ![]() $(?)^\bullet$ for
$(?)^\bullet$ for ![]() $?=C, D,W$. We say
$?=C, D,W$. We say ![]() $S_W$ is a correspondence from
$S_W$ is a correspondence from ![]() $C^\bullet$ to
$C^\bullet$ to ![]() $D^\bullet$. If all of
$D^\bullet$. If all of ![]() $C^\bullet$,
$C^\bullet$, ![]() $D^\bullet$ and
$D^\bullet$ and ![]() $W^\bullet$ are Segal objects of
$W^\bullet$ are Segal objects of ![]() $\mathcal {C}$, then we say
$\mathcal {C}$, then we say ![]() $S_W$ is a correspondence of Segal objects from
$S_W$ is a correspondence of Segal objects from ![]() $C^\bullet$ to
$C^\bullet$ to ![]() $D^\bullet$. The composition
$D^\bullet$. The composition ![]() $S_W\circ F_{{\bigcirc{\kern-6pt \star}}, \mathcal {T}_+}$ gives a functor
$S_W\circ F_{{\bigcirc{\kern-6pt \star}}, \mathcal {T}_+}$ gives a functor ![]() $I_{N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}} [1]}\underset {I_+}{\times }\mathcal {T}_+\rightarrow \mathcal {C}$, which also gives a functor
$I_{N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}} [1]}\underset {I_+}{\times }\mathcal {T}_+\rightarrow \mathcal {C}$, which also gives a functor ![]() $I^\natural _{N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}} [1]}\underset {I_+}{\times }\mathcal {T}^\natural _+\rightarrow (\mathcal {C}\times I_+)^\natural$ over
$I^\natural _{N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}} [1]}\underset {I_+}{\times }\mathcal {T}^\natural _+\rightarrow (\mathcal {C}\times I_+)^\natural$ over ![]() $I_+$.
$I_+$.
Next, we take the right Kan extension of ![]() $S_W\circ F_{{\bigcirc{\kern-6pt \star}}, \mathcal {T}_+}$ along the projection
$S_W\circ F_{{\bigcirc{\kern-6pt \star}}, \mathcal {T}_+}$ along the projection ![]() $p_{\mathcal {T}_+}: I_{N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}} [1]}\underset {I_+}{\times }\mathcal {T}_+\rightarrow I_{N(\Delta )^{\textrm {op}}{\bigcirc{\kern-6pt \star}} [1]}\underset {I}{\times }\mathcal {T}$ defined by forgetting the coordinate
$p_{\mathcal {T}_+}: I_{N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}} [1]}\underset {I_+}{\times }\mathcal {T}_+\rightarrow I_{N(\Delta )^{\textrm {op}}{\bigcirc{\kern-6pt \star}} [1]}\underset {I}{\times }\mathcal {T}$ defined by forgetting the coordinate ![]() $\{0\}_1,\{0\}_2,\{1\}$ in
$\{0\}_1,\{0\}_2,\{1\}$ in ![]() $\mathcal {T}_+$. This gives the desired functor
$\mathcal {T}_+$. This gives the desired functor
which also lies in
 \begin{align*}
\mathrm{Maps}_{I}(I^\natural_{N(\Delta)^{\rm op}{\bigcirc{\kern-6pt \star}}
[1]}\underset{I}{\times}\mathcal{T}^\natural,
(\mathcal{C}\times I)^\natural)&\simeq\mathrm{Maps}_I(I^\natural_{N(\Delta)^{\rm
op}{\bigcirc{\kern-6pt \star}} [1]},
(\mathcal{C}^\natural)^{\mathcal{T}^\natural})\\
&\simeq\mathrm{Maps}_{(1\text{-}\mathcal{C}\mathrm{at})^{\Delta^{\rm
op}}_{/\mathrm{Seq}_\bullet
(N(\Delta)^{\rm
op})}}(\mathrm{Seq}_\bullet(N(\Delta)^{\rm
op}{\bigcirc{\kern-6pt \star}}
[1]),f_{\Delta^\bullet}^\mathcal{C}),
\end{align*}
\begin{align*}
\mathrm{Maps}_{I}(I^\natural_{N(\Delta)^{\rm op}{\bigcirc{\kern-6pt \star}}
[1]}\underset{I}{\times}\mathcal{T}^\natural,
(\mathcal{C}\times I)^\natural)&\simeq\mathrm{Maps}_I(I^\natural_{N(\Delta)^{\rm
op}{\bigcirc{\kern-6pt \star}} [1]},
(\mathcal{C}^\natural)^{\mathcal{T}^\natural})\\
&\simeq\mathrm{Maps}_{(1\text{-}\mathcal{C}\mathrm{at})^{\Delta^{\rm
op}}_{/\mathrm{Seq}_\bullet
(N(\Delta)^{\rm
op})}}(\mathrm{Seq}_\bullet(N(\Delta)^{\rm
op}{\bigcirc{\kern-6pt \star}}
[1]),f_{\Delta^\bullet}^\mathcal{C}),
\end{align*}
where ![]() $f_{\Delta ^\bullet }^\mathcal {C}$ was defined in (2.3.2). In the following, we also think of
$f_{\Delta ^\bullet }^\mathcal {C}$ was defined in (2.3.2). In the following, we also think of ![]() $F_{{\bigcirc{\kern-6pt \star}},S_W}$ as a functor
$F_{{\bigcirc{\kern-6pt \star}},S_W}$ as a functor ![]() $\mathrm {Seq}_\bullet (N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1])\rightarrow f_{\Delta ^\bullet }^\mathcal {C}$ over
$\mathrm {Seq}_\bullet (N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1])\rightarrow f_{\Delta ^\bullet }^\mathcal {C}$ over ![]() $\mathrm {Seq}_\bullet (N(\Delta )^{\rm op})$. In a totally similar fashion, we can define a functor
$\mathrm {Seq}_\bullet (N(\Delta )^{\rm op})$. In a totally similar fashion, we can define a functor
from any correspondence ![]() $D^\bullet \leftarrow W^\bullet \rightarrow C^\bullet$ of
$D^\bullet \leftarrow W^\bullet \rightarrow C^\bullet$ of ![]() $\mathrm {Fin}_*$-objects in
$\mathrm {Fin}_*$-objects in ![]() $\mathcal {C}$ from
$\mathcal {C}$ from ![]() $C^\bullet$ to
$C^\bullet$ to ![]() $D^\bullet$.
$D^\bullet$.
2.4.2 Right-lax homomorphism from correspondence of simplicial/  $\mathrm {Fin}_*$-objects
$\mathrm {Fin}_*$-objects
Theorem 2.13 Let ![]() $D^\bullet \leftarrow W^\bullet \rightarrow C^\bullet$ be a correspondence of simplicial (respectively,
$D^\bullet \leftarrow W^\bullet \rightarrow C^\bullet$ be a correspondence of simplicial (respectively, ![]() $\mathrm {Fin}_*$-) objects (from
$\mathrm {Fin}_*$-) objects (from ![]() $C^\bullet$ to
$C^\bullet$ to ![]() $D^\bullet$). Suppose that
$D^\bullet$). Suppose that ![]() $C^\bullet$ and
$C^\bullet$ and ![]() $D^\bullet$ represent associative (respectively, commutative) algebra objects in
$D^\bullet$ represent associative (respectively, commutative) algebra objects in ![]() $\mathbf {Corr}(\mathcal {C}^\times )$. Then
$\mathbf {Corr}(\mathcal {C}^\times )$. Then ![]() $F_{{\bigcirc{\kern-6pt \star}}, S_W}$ (2.4.6) (respectively,
$F_{{\bigcirc{\kern-6pt \star}}, S_W}$ (2.4.6) (respectively, ![]() $F_{{\bigcirc{\kern-6pt \star}}, S_W}^\mathrm {Comm}$ (2.4.7)) gives a right-lax homomorphism between the associative (respectively, commutative) algebra objects if and only if
$F_{{\bigcirc{\kern-6pt \star}}, S_W}^\mathrm {Comm}$ (2.4.7)) gives a right-lax homomorphism between the associative (respectively, commutative) algebra objects if and only if ![]() $W^\bullet$ represents another associative (respectively, commutative) algebra object and the following diagrams are Cartesian in
$W^\bullet$ represents another associative (respectively, commutative) algebra object and the following diagrams are Cartesian in ![]() $\mathcal {C}$
$\mathcal {C}$

for any ![]() $[k]\in N(\Delta )^{\rm op}$ (respectively,
$[k]\in N(\Delta )^{\rm op}$ (respectively,

for any ![]() $\langle n\rangle \in N(\mathrm {Fin}_*)$).
$\langle n\rangle \in N(\mathrm {Fin}_*)$).
Moreover, if the following diagrams are also Cartesian in ![]() $\mathcal {C}$
$\mathcal {C}$

for the unique active ![]() $f: [1]\rightarrow [2]$ in
$f: [1]\rightarrow [2]$ in ![]() $N(\Delta )$ (respectively,
$N(\Delta )$ (respectively,

for the unique active ![]() $f: \langle 2\rangle \rightarrow \langle 1\rangle$ in
$f: \langle 2\rangle \rightarrow \langle 1\rangle$ in ![]() $N(\mathrm {Fin}_*)$), then
$N(\mathrm {Fin}_*)$), then ![]() $F_{{\bigcirc{\kern-6pt \star}}, S_W}$ (respectively,
$F_{{\bigcirc{\kern-6pt \star}}, S_W}$ (respectively, ![]() $F_{{\bigcirc{\kern-6pt \star}}, S_W}^\mathrm {Comm}$) induces an algebra homomorphism between the associative (respectively, commutative) algebra objects in
$F_{{\bigcirc{\kern-6pt \star}}, S_W}^\mathrm {Comm}$) induces an algebra homomorphism between the associative (respectively, commutative) algebra objects in ![]() $\mathrm {Corr}(\mathcal {C})$.
$\mathrm {Corr}(\mathcal {C})$.
Proof. We will only prove the associative case; the commutative case follows in a completely similar way. Like in the proof of Theorem 2.8, to make ![]() $F_{{\bigcirc{\kern-6pt \star}},S_W}$ correspond to a functor
$F_{{\bigcirc{\kern-6pt \star}},S_W}$ correspond to a functor ![]() $N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1]\rightarrow \mathbf {Corr}(\mathcal {C})^{\otimes,\Delta ^{\textrm {op}}}$ over
$N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1]\rightarrow \mathbf {Corr}(\mathcal {C})^{\otimes,\Delta ^{\textrm {op}}}$ over ![]() $N(\Delta )^{\rm op}$, we just need
$N(\Delta )^{\rm op}$, we just need ![]() $F_{{\bigcirc{\kern-6pt \star}},S_W}$ to send any object
$F_{{\bigcirc{\kern-6pt \star}},S_W}$ to send any object ![]() $([n]; \alpha,\beta,\tau _0,\tau _1)\in \mathrm {Seq}_n(N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1])$ to an element
$([n]; \alpha,\beta,\tau _0,\tau _1)\in \mathrm {Seq}_n(N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1])$ to an element ![]() $F\in \mathrm {Fun}''(([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}},\mathcal {C}^{\times,\Delta })$, i.e.
$F\in \mathrm {Fun}''(([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}},\mathcal {C}^{\times,\Delta })$, i.e. ![]() $F$ satisfying (Obj) below (2.2.2), and for any morphism
$F$ satisfying (Obj) below (2.2.2), and for any morphism ![]() $(([n]; \alpha,\beta,\tau _0,\tau _1)\rightarrow ([n]; \alpha,\beta,\tau '_0,\tau '_1))$ to a morphism
$(([n]; \alpha,\beta,\tau _0,\tau _1)\rightarrow ([n]; \alpha,\beta,\tau '_0,\tau '_1))$ to a morphism ![]() $q: F\rightarrow F'$ satisfying (Mor) below (2.2.2). It is clear from the construction of
$q: F\rightarrow F'$ satisfying (Mor) below (2.2.2). It is clear from the construction of ![]() $F_{{\bigcirc{\kern-6pt \star}},S_W}$ that the latter is satisfied by
$F_{{\bigcirc{\kern-6pt \star}},S_W}$ that the latter is satisfied by ![]() $F_{{\bigcirc{\kern-6pt \star}}, S_W}$ regardless of the conditions on
$F_{{\bigcirc{\kern-6pt \star}}, S_W}$ regardless of the conditions on ![]() $C^\bullet, W^\bullet, D^\bullet$.
$C^\bullet, W^\bullet, D^\bullet$.
For any ![]() $([n]; \alpha,\beta,\tau _0,\tau _1)\in \mathrm {Seq}_n(N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1])$, its image under
$([n]; \alpha,\beta,\tau _0,\tau _1)\in \mathrm {Seq}_n(N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1])$, its image under ![]() $F_{{\bigcirc{\kern-6pt \star}}, S_W}$ is a functor
$F_{{\bigcirc{\kern-6pt \star}}, S_W}$ is a functor ![]() $F_{([n],s^\tau )}: ([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}\underset {N(\Delta )}{\times } T\rightarrow \mathcal {C}$ in
$F_{([n],s^\tau )}: ([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}\underset {N(\Delta )}{\times } T\rightarrow \mathcal {C}$ in ![]() $\mathcal {C}$ which takes
$\mathcal {C}$ which takes
 \begin{align} ((i,j), [u,u+1])\mapsto\
& C^{[\alpha_{ji}(u), \alpha_{ji}(u+1)]},\quad i\leq j\leq \mu-1\nonumber\\ ((i, \mu+j),[u,u+1])\mapsto\
& W^{[\tau_1\beta_{j,0}(u),\tau_1\beta_{j,0}(u+1)]}\nonumber\\
&\quad \underset{C^{[\tau_1\beta_{j,0}(u),\tau_1\beta_{j,0}(u+1)]}}{\times}C^{[\alpha_{\mu-1,i}\tau_0\tau_1\beta_{j,0}(u),
\alpha_{\mu-1,i}\tau_0\tau_1\beta_{j,0}(u+1)]}\nonumber\\
& 0\leq i\leq \mu-1, 0\leq j\leq n-\mu\\
(\mu+i,\mu+j; [u,u+1])\mapsto\
& D^{[\beta_{ji}(u),\beta_{ji}(u+1)]},\quad 0\leq i\leq j\leq
n-\mu. \nonumber
\end{align}
\begin{align} ((i,j), [u,u+1])\mapsto\
& C^{[\alpha_{ji}(u), \alpha_{ji}(u+1)]},\quad i\leq j\leq \mu-1\nonumber\\ ((i, \mu+j),[u,u+1])\mapsto\
& W^{[\tau_1\beta_{j,0}(u),\tau_1\beta_{j,0}(u+1)]}\nonumber\\
&\quad \underset{C^{[\tau_1\beta_{j,0}(u),\tau_1\beta_{j,0}(u+1)]}}{\times}C^{[\alpha_{\mu-1,i}\tau_0\tau_1\beta_{j,0}(u),
\alpha_{\mu-1,i}\tau_0\tau_1\beta_{j,0}(u+1)]}\nonumber\\
& 0\leq i\leq \mu-1, 0\leq j\leq n-\mu\\
(\mu+i,\mu+j; [u,u+1])\mapsto\
& D^{[\beta_{ji}(u),\beta_{ji}(u+1)]},\quad 0\leq i\leq j\leq
n-\mu. \nonumber
\end{align} Now assume ![]() $C^\bullet \leftarrow W^\bullet \rightarrow D^\bullet$ is a correspondence of simplicial objects with
$C^\bullet \leftarrow W^\bullet \rightarrow D^\bullet$ is a correspondence of simplicial objects with ![]() $C^\bullet$ and
$C^\bullet$ and ![]() $D^\bullet$ representing algebra objects in
$D^\bullet$ representing algebra objects in ![]() $\mathrm {Corr}(\mathcal {C})$. Let
$\mathrm {Corr}(\mathcal {C})$. Let ![]() $WCC^{\alpha,\beta,\tau }_{i, j;u}$ denote the fiber product on the right-hand side of (2.4.12). Then to show that
$WCC^{\alpha,\beta,\tau }_{i, j;u}$ denote the fiber product on the right-hand side of (2.4.12). Then to show that ![]() $F_{([n],s^\tau )}$ satisfies (Obj), it suffices to check that the following diagrams are Cartesian in
$F_{([n],s^\tau )}$ satisfies (Obj), it suffices to check that the following diagrams are Cartesian in ![]() $\mathcal {C}$:
$\mathcal {C}$:


The first diagram (2.4.13) is Cartesian directly follows from the assumption that ![]() $C^\bullet$ represents an algebra object, and the second (2.4.14) is Cartesian is equivalent to the condition that the following diagram
$C^\bullet$ represents an algebra object, and the second (2.4.14) is Cartesian is equivalent to the condition that the following diagram

is Cartesian for any ![]() $f: [k]\rightarrow [\ell ]$ in
$f: [k]\rightarrow [\ell ]$ in ![]() $N(\Delta )$. The latter is equivalent to the assumptions on
$N(\Delta )$. The latter is equivalent to the assumptions on ![]() $W^\bullet$ in the theorem. Thus, this proves part (a).
$W^\bullet$ in the theorem. Thus, this proves part (a).
For the second part, we just need to check that for any morphism ![]() $([n],\alpha,\beta ;\tau _0,\tau _1)\rightarrow ([n],\alpha,\beta ;\tau _0',\tau _1')$ in
$([n],\alpha,\beta ;\tau _0,\tau _1)\rightarrow ([n],\alpha,\beta ;\tau _0',\tau _1')$ in ![]() $\mathrm {Seq}_n(N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1])$ induced by
$\mathrm {Seq}_n(N(\Delta )^{\rm op}{\bigcirc{\kern-6pt \star}}[1])$ induced by ![]() $\tau : [\xi ']\rightarrow [\xi ]$ in
$\tau : [\xi ']\rightarrow [\xi ]$ in ![]() $N(\Delta )$, the morphisms
$N(\Delta )$, the morphisms
are isomorphisms for ![]() $0\leq i\leq \mu -1, 0\leq j\leq n-\mu$. It then suffices to show that for any
$0\leq i\leq \mu -1, 0\leq j\leq n-\mu$. It then suffices to show that for any ![]() $[n]\overset {f}{\rightarrow } [m]\overset {g}{\rightarrow } [k]$ in
$[n]\overset {f}{\rightarrow } [m]\overset {g}{\rightarrow } [k]$ in ![]() $N(\Delta )$, the following diagram is Cartesian.
$N(\Delta )$, the following diagram is Cartesian.

These are exactly the diagrams

for the unique active ![]() $f: [1]\rightarrow [\ell ]$ for each
$f: [1]\rightarrow [\ell ]$ for each ![]() $[\ell ]$ in
$[\ell ]$ in ![]() $N(\Delta )$. This can be easily reduced to the case for
$N(\Delta )$. This can be easily reduced to the case for ![]() $\ell =2$. Alternatively, one can directly get to this from the characterization of algebra homomorphisms out of right-lax homomorphisms. Thus, the second part is established.
$\ell =2$. Alternatively, one can directly get to this from the characterization of algebra homomorphisms out of right-lax homomorphisms. Thus, the second part is established.
Now Theorem 2.13 immediately implies the following.
Corollary 2.14
(a) Any correspondence of Segal objects (respectively, commutative Segal objects)
 $D^\bullet \leftarrow W^\bullet \rightarrow C^\bullet$ gives a right-lax homomorphism from the associative algebra object (respectively, commutative algebra object) in
$D^\bullet \leftarrow W^\bullet \rightarrow C^\bullet$ gives a right-lax homomorphism from the associative algebra object (respectively, commutative algebra object) in  $\mathbf {Corr}(\mathcal {C}^\times )$ represented by
$\mathbf {Corr}(\mathcal {C}^\times )$ represented by  $C^\bullet$ to that represented by
$C^\bullet$ to that represented by  $D^\bullet$.
$D^\bullet$.(b) In the same setting as part (a), if the correspondence further satisfies that the following diagram is Cartesian in
 $\mathcal {C}$,
(2.4.17)(respectively,
$\mathcal {C}$,
(2.4.17)(respectively, (2.4.18)where the vertical maps are induced by the unique active map
(2.4.18)where the vertical maps are induced by the unique active map
 $[1]\rightarrow [2]$ in
$[1]\rightarrow [2]$ in  $N(\Delta )$ (respectively,
$N(\Delta )$ (respectively,  $\langle 2\rangle \rightarrow \langle 1\rangle$ in
$\langle 2\rangle \rightarrow \langle 1\rangle$ in  $N(\mathrm {Fin}_*)$), then it gives a homomorphism in
$N(\mathrm {Fin}_*)$), then it gives a homomorphism in  $\mathrm {Corr}(\mathcal {C}^\times )$ between the corresponding associative (respectively, commutative) algebra objects.
$\mathrm {Corr}(\mathcal {C}^\times )$ between the corresponding associative (respectively, commutative) algebra objects.
Remark 2.15 From the above description, it is easy to see that the composition of two (right-lax) homomorphisms between (commutative) algebra objects given by correspondences
of simplicial objects (respectively, ![]() $\mathrm {Fin}_*$-objects). The composition is homotopic to the one given by the correspondences
$\mathrm {Fin}_*$-objects). The composition is homotopic to the one given by the correspondences
Moreover, using the machinery that we have developed, one can construct functors
 \begin{align*} &\mathrm{Corr}(\mathrm{Fun}'(N(\mathrm{Fin}_*),\mathcal{C}^\times))_{\mathsf{inert}, \mathsf{all}}\rightarrow \mathrm{CAlg}(\mathbf{Corr}(\mathcal{C}^\times))^{\mathrm{R}\text{-}\mathrm{lax}},\\ &\mathrm{Corr}(\mathrm{Fun}'(N(\mathrm{Fin}_*),\mathcal{C}^\times))_{\mathsf{inert}, \mathsf{active}}\rightarrow \mathrm{CAlg}(\mathbf{Corr}(\mathcal{C}^\times)), \end{align*}
\begin{align*} &\mathrm{Corr}(\mathrm{Fun}'(N(\mathrm{Fin}_*),\mathcal{C}^\times))_{\mathsf{inert}, \mathsf{all}}\rightarrow \mathrm{CAlg}(\mathbf{Corr}(\mathcal{C}^\times))^{\mathrm{R}\text{-}\mathrm{lax}},\\ &\mathrm{Corr}(\mathrm{Fun}'(N(\mathrm{Fin}_*),\mathcal{C}^\times))_{\mathsf{inert}, \mathsf{active}}\rightarrow \mathrm{CAlg}(\mathbf{Corr}(\mathcal{C}^\times)), \end{align*}
where ![]() $\mathrm {Fun}'(N(\mathrm {Fin}_*),\mathcal {C}^\times )$ is the full subcategory of
$\mathrm {Fun}'(N(\mathrm {Fin}_*),\mathcal {C}^\times )$ is the full subcategory of ![]() $\mathrm {Fun}(N(\mathrm {Fin}_*),\mathcal {C}^\times )$ consisting of
$\mathrm {Fun}(N(\mathrm {Fin}_*),\mathcal {C}^\times )$ consisting of ![]() $\mathrm {Fin}_*$-objects satisfying the condition in Theorem 2.8,
$\mathrm {Fin}_*$-objects satisfying the condition in Theorem 2.8, ![]() $\mathsf {inert}$ (respectively,
$\mathsf {inert}$ (respectively, ![]() $\mathsf {active}$) is the class of morphisms satisfying that (2.4.9) (respectively, (2.4.11))) is Cartesian. There is an obvious analogue for the associative case. It is reasonable to expect that the functors are equivalences and we will address this in a separate note.
$\mathsf {active}$) is the class of morphisms satisfying that (2.4.9) (respectively, (2.4.11))) is Cartesian. There is an obvious analogue for the associative case. It is reasonable to expect that the functors are equivalences and we will address this in a separate note.
Let ![]() $\mathrm {Fun}_{\mathsf {inert}}(N(\Delta )^{\rm op}, \mathcal {C})$ (respectively,
$\mathrm {Fun}_{\mathsf {inert}}(N(\Delta )^{\rm op}, \mathcal {C})$ (respectively, ![]() $\mathrm {Fun}_{\mathsf {inert}}(N(\mathrm {Fin}_*), \mathcal {C})$) be the 1-full subcategory of
$\mathrm {Fun}_{\mathsf {inert}}(N(\mathrm {Fin}_*), \mathcal {C})$) be the 1-full subcategory of ![]() $\mathrm {Fun}(N(\Delta )^{\rm op}, \mathcal {C})$ (respectively,
$\mathrm {Fun}(N(\Delta )^{\rm op}, \mathcal {C})$ (respectively, ![]() $\mathrm {Fun}(N(\mathrm {Fin}_*), \mathcal {C})$) consisting of simplicial objects (respectively,
$\mathrm {Fun}(N(\mathrm {Fin}_*), \mathcal {C})$) consisting of simplicial objects (respectively, ![]() $\mathrm {Fin}_*$-objects) in
$\mathrm {Fin}_*$-objects) in ![]() $\mathcal {C}$ that satisfy the condition in Theorem 2.8(i) (respectively, Theorem 2.8(ii)), and whose morphisms from
$\mathcal {C}$ that satisfy the condition in Theorem 2.8(i) (respectively, Theorem 2.8(ii)), and whose morphisms from ![]() $W^\bullet$ to
$W^\bullet$ to ![]() $D^\bullet$ consisting of those satisfying (2.4.8) (respectively, (2.4.9)). It is not hard to deduce from the above constructions the following proposition.
$D^\bullet$ consisting of those satisfying (2.4.8) (respectively, (2.4.9)). It is not hard to deduce from the above constructions the following proposition.
Proposition 2.16 There are natural functors
 \begin{align*} &\mathrm{Fun}_{\mathsf{inert}}(N(\Delta)^{\rm op}, \mathcal{C})\rightarrow \mathrm{Assoc}\mathrm{Alg}(\mathrm{Corr}(\mathcal{C}^\times)),\\ &\mathrm{Fun}_{\mathsf{inert}}(N(\mathrm{Fin}_*), \mathcal{C})\rightarrow \mathrm{Comm}\mathrm{Alg}(\mathrm{Corr}(\mathcal{C}^\times)), \end{align*}
\begin{align*} &\mathrm{Fun}_{\mathsf{inert}}(N(\Delta)^{\rm op}, \mathcal{C})\rightarrow \mathrm{Assoc}\mathrm{Alg}(\mathrm{Corr}(\mathcal{C}^\times)),\\ &\mathrm{Fun}_{\mathsf{inert}}(N(\mathrm{Fin}_*), \mathcal{C})\rightarrow \mathrm{Comm}\mathrm{Alg}(\mathrm{Corr}(\mathcal{C}^\times)), \end{align*}
that send every object ![]() $C^\bullet$ on the left-hand side to the associative/commutative algebra object assigned in Theorem 2.8.
$C^\bullet$ on the left-hand side to the associative/commutative algebra object assigned in Theorem 2.8.
Proof. We will prove the commutative case; the associative case is entirely similar. Let ![]() $I_{\Delta ^n}\rightarrow N(\Delta )^{\rm op}$ (respectively,
$I_{\Delta ^n}\rightarrow N(\Delta )^{\rm op}$ (respectively, ![]() $I_{\Delta ^n\times N(\mathrm {Fin}_*)}\rightarrow N(\Delta )^{\rm op}$) be the coCartesian fibration of ordinary 1-categories from the Grothendieck construction of
$I_{\Delta ^n\times N(\mathrm {Fin}_*)}\rightarrow N(\Delta )^{\rm op}$) be the coCartesian fibration of ordinary 1-categories from the Grothendieck construction of ![]() $\mathrm {Seq}_\bullet (\Delta ^n): N(\Delta )^{\rm op}\rightarrow 1\text {-}\mathcal {C}\mathrm {at}^{\mathrm {ord}}$ (respectively,
$\mathrm {Seq}_\bullet (\Delta ^n): N(\Delta )^{\rm op}\rightarrow 1\text {-}\mathcal {C}\mathrm {at}^{\mathrm {ord}}$ (respectively, ![]() $\mathrm {Seq}_\bullet (N(\mathrm {Fin}_*)\times \Delta ^n): N(\Delta )^{\rm op}\rightarrow 1\text {-}\mathcal {C}\mathrm {at}^{\mathrm {ord}}$). Then we have an isomorphism of coCartesian fibrations over
$\mathrm {Seq}_\bullet (N(\mathrm {Fin}_*)\times \Delta ^n): N(\Delta )^{\rm op}\rightarrow 1\text {-}\mathcal {C}\mathrm {at}^{\mathrm {ord}}$). Then we have an isomorphism of coCartesian fibrations over ![]() $I^\mathrm {Comm}$.
$I^\mathrm {Comm}$.
We will define the sought-for functor by first exhibiting a morphism in ![]() $\mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}}$:
$\mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}}$:
To this end, we just need to construct a natural morphism
in ![]() $(1\text {-}\mathcal {C}\mathrm {at})^{\Delta }$. The construction is very similar to that of (2.3.12). For any
$(1\text {-}\mathcal {C}\mathrm {at})^{\Delta }$. The construction is very similar to that of (2.3.12). For any ![]() $[n]\in N(\Delta )^{\rm op}$, the fiber of
$[n]\in N(\Delta )^{\rm op}$, the fiber of
over ![]() $[n]$ is
$[n]$ is ![]() $\mathrm {Seq}_n(\Delta ^\bullet )\times (\bigsqcup _{s\in \mathrm {Seq}_n(N(\mathrm {Fin}_*))}\mathcal {T}^\mathrm {Comm}_{([n],s)})$. Now we define
$\mathrm {Seq}_n(\Delta ^\bullet )\times (\bigsqcup _{s\in \mathrm {Seq}_n(N(\mathrm {Fin}_*))}\mathcal {T}^\mathrm {Comm}_{([n],s)})$. Now we define
 \begin{align} &\mathrm{Seq}_n(\Delta^\bullet)\times \bigg(\bigsqcup_{s\in \mathrm{Seq}_n(N(\mathrm{Fin}_*))}\mathcal{T}^\mathrm{Comm}_{([n],s)}\bigg)\rightarrow \Delta^\bullet\times N(\mathrm{Fin}_*)\nonumber\\ &(\vartheta^{(m)}; (s, (i,j), u))\mapsto (\vartheta^{(m)}(i); s_{i,j}^{-1}(u)\sqcup\{*\}), \end{align}
\begin{align} &\mathrm{Seq}_n(\Delta^\bullet)\times \bigg(\bigsqcup_{s\in \mathrm{Seq}_n(N(\mathrm{Fin}_*))}\mathcal{T}^\mathrm{Comm}_{([n],s)}\bigg)\rightarrow \Delta^\bullet\times N(\mathrm{Fin}_*)\nonumber\\ &(\vartheta^{(m)}; (s, (i,j), u))\mapsto (\vartheta^{(m)}(i); s_{i,j}^{-1}(u)\sqcup\{*\}), \end{align}
in which ![]() $\vartheta ^{(m)}: \Delta ^n\rightarrow \Delta ^m$ represents an element in
$\vartheta ^{(m)}: \Delta ^n\rightarrow \Delta ^m$ represents an element in ![]() $\mathrm {Seq}_n(\Delta ^m)$ and the functor on morphisms is the obvious one. With the input from
$\mathrm {Seq}_n(\Delta ^m)$ and the functor on morphisms is the obvious one. With the input from ![]() $F_{\mathcal {T}^\mathrm {Comm}, \mathrm {Fin}_*}$, the functors (2.4.23) for different
$F_{\mathcal {T}^\mathrm {Comm}, \mathrm {Fin}_*}$, the functors (2.4.23) for different ![]() $[n]\in N(\Delta )^{\rm op}$ assemble to be the desired morphism (2.4.22). It is easy to see that the image under (2.4.21) of any object in
$[n]\in N(\Delta )^{\rm op}$ assemble to be the desired morphism (2.4.22). It is easy to see that the image under (2.4.21) of any object in ![]() $\mathrm {Seq}_\bullet (\mathrm {Fun}(N(\mathrm {Fin}_*),\mathcal {C}))$ lies in
$\mathrm {Seq}_\bullet (\mathrm {Fun}(N(\mathrm {Fin}_*),\mathcal {C}))$ lies in ![]() $\mathrm {Maps}_{I^\mathrm {Comm}}(I^\natural _{\Delta ^\bullet \times N(\mathrm {Fin}_*)}\underset {I^\mathrm {Comm}}{\times }(\mathcal {T}^\mathrm {Comm})^\natural, (\mathcal {C}\times I^\mathrm {Comm})^\natural )$, therefore we have a well-defined morphism in
$\mathrm {Maps}_{I^\mathrm {Comm}}(I^\natural _{\Delta ^\bullet \times N(\mathrm {Fin}_*)}\underset {I^\mathrm {Comm}}{\times }(\mathcal {T}^\mathrm {Comm})^\natural, (\mathcal {C}\times I^\mathrm {Comm})^\natural )$, therefore we have a well-defined morphism in ![]() $\mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}}$:
$\mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}}$:
Lastly, one just need to check that the image of any object in (2.4.24) gives rise to a functor ![]() $\Delta ^k\times N(\mathrm {Fin}_*)\rightarrow \mathrm {Corr}(\mathcal {C})^{\otimes, \mathrm {Fin}_*}$ over
$\Delta ^k\times N(\mathrm {Fin}_*)\rightarrow \mathrm {Corr}(\mathcal {C})^{\otimes, \mathrm {Fin}_*}$ over ![]() $N(\mathrm {Fin}_*)$ for any
$N(\mathrm {Fin}_*)$ for any ![]() $k$. Like in the proof of Theorem 2.8, this is guaranteed by the assumptions on objects and morphisms in
$k$. Like in the proof of Theorem 2.8, this is guaranteed by the assumptions on objects and morphisms in ![]() $\mathrm {Fun}_{\mathsf {inert}}(N(\mathrm {Fin}_*),\mathcal {C})$.
$\mathrm {Fun}_{\mathsf {inert}}(N(\mathrm {Fin}_*),\mathcal {C})$.
An immediate corollary of Proposition 2.16 is the following.
Corollary 2.17 [Reference Gaitsgory and RozenblyumGR17, Chapter 9, Corollary 4.4.5]
For any ![]() $c\in \mathcal {C}$, there is a canonically defined functor
$c\in \mathcal {C}$, there is a canonically defined functor
Let ![]() $\mathrm {Fun}_{\mathsf {active}}(N(\Delta )^{\rm op}, \mathcal {C})$ (respectively,
$\mathrm {Fun}_{\mathsf {active}}(N(\Delta )^{\rm op}, \mathcal {C})$ (respectively, ![]() $\mathrm {Fun}_{\mathsf {active}}(N(\mathrm {Fin}_*), \mathcal {C})$) be the 1-full subcategory of
$\mathrm {Fun}_{\mathsf {active}}(N(\mathrm {Fin}_*), \mathcal {C})$) be the 1-full subcategory of ![]() $\mathrm {Fun}(N(\Delta )^{\rm op},\mathcal {C})$ (respectively,
$\mathrm {Fun}(N(\Delta )^{\rm op},\mathcal {C})$ (respectively, ![]() $\mathrm {Fun}(N(\mathrm {Fin}_*), \mathcal {C})$) consisting of the simplicial (
$\mathrm {Fun}(N(\mathrm {Fin}_*), \mathcal {C})$) consisting of the simplicial (![]() $\mathrm {Fin}_*$-) objects in
$\mathrm {Fin}_*$-) objects in ![]() $\mathcal {C}$ that satisfy the condition in Theorem 2.8(i) (respectively, Theorem 2.8(ii)), whose morphisms from
$\mathcal {C}$ that satisfy the condition in Theorem 2.8(i) (respectively, Theorem 2.8(ii)), whose morphisms from ![]() $W^\bullet$ to
$W^\bullet$ to ![]() $C^\bullet$ consist of those satisfying (2.4.10) (respectively, (2.4.11)).
$C^\bullet$ consist of those satisfying (2.4.10) (respectively, (2.4.11)).
Proposition 2.18 There are natural functors
that send every object ![]() $C^\bullet$ on the left-hand side to the associative/commutative algebra object assigned in Theorem 2.8.
$C^\bullet$ on the left-hand side to the associative/commutative algebra object assigned in Theorem 2.8.
Proof. The idea is similar to that of Proposition 2.16. In the commutative case, we define a functor
 \begin{align*} & I_{\Delta^\bullet}\underset{N(\Delta)^{\rm op}}{\times}\mathcal{T}^\mathrm{Comm}\rightarrow (\Delta^\bullet)^{\rm op}\times N(\mathrm{Fin}_*)\\ &([n]; \vartheta^{(m)}; (s,(i,j),u))\mapsto ((\vartheta^{(m)})^{\rm op}(j); s_{i,j}^{-1}(u)\sqcup\{*\}), \end{align*}
\begin{align*} & I_{\Delta^\bullet}\underset{N(\Delta)^{\rm op}}{\times}\mathcal{T}^\mathrm{Comm}\rightarrow (\Delta^\bullet)^{\rm op}\times N(\mathrm{Fin}_*)\\ &([n]; \vartheta^{(m)}; (s,(i,j),u))\mapsto ((\vartheta^{(m)})^{\rm op}(j); s_{i,j}^{-1}(u)\sqcup\{*\}), \end{align*}
where ![]() $(\vartheta ^{(m)}; (s,(i,j),u))$ is in the fiber of
$(\vartheta ^{(m)}; (s,(i,j),u))$ is in the fiber of ![]() $I_{\Delta ^\bullet }\underset {N(\Delta )^{\rm op}}{\times }\mathcal {T}^\mathrm {Comm}$ over
$I_{\Delta ^\bullet }\underset {N(\Delta )^{\rm op}}{\times }\mathcal {T}^\mathrm {Comm}$ over ![]() $[n]$ (cf. (2.4.23)). This induces a functor
$[n]$ (cf. (2.4.23)). This induces a functor
for any ![]() $\mathcal {C}$ and, hence, a morphism in
$\mathcal {C}$ and, hence, a morphism in ![]() $\mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}}$:
$\mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}}$:
It is straightforward to see that the restriction of the morphism (2.4.27) to the simplicial subspace ![]() $\mathrm {Seq}_\bullet (\mathrm {Fun}_{\mathsf {active}}(N(\mathrm {Fin}_*),\mathcal {C})^{\rm op})$ induces the desired functor (2.4.26).
$\mathrm {Seq}_\bullet (\mathrm {Fun}_{\mathsf {active}}(N(\mathrm {Fin}_*),\mathcal {C})^{\rm op})$ induces the desired functor (2.4.26).
The proof for the associative case proceeds in the same vein.
Proposition 2.19 Let ![]() $K,L$ be two
$K,L$ be two ![]() $\infty$-categories. Assume
$\infty$-categories. Assume ![]() $F: K\times L^{\rm op}\rightarrow \mathrm {Fun}(N(\mathrm {Fin}_*), \mathcal {C})$ is a functor satisfying:
$F: K\times L^{\rm op}\rightarrow \mathrm {Fun}(N(\mathrm {Fin}_*), \mathcal {C})$ is a functor satisfying:
(i) for any
 $\ell \in L$ (respectively,
$\ell \in L$ (respectively,  $k\in K$),
$k\in K$),  $F|_{K\times \{\ell \}}$ (respectively,
$F|_{K\times \{\ell \}}$ (respectively,  $F|_{\{k\}\times L^{\rm op}}$) factors through the 1-full subcategory
$F|_{\{k\}\times L^{\rm op}}$) factors through the 1-full subcategory  $\mathrm {Fun}_{\mathsf {inert}}(N(\mathrm {Fin}_*), \mathcal {C})$ (respectively,
$\mathrm {Fun}_{\mathsf {inert}}(N(\mathrm {Fin}_*), \mathcal {C})$ (respectively,  $\mathrm {Fun}_{\mathsf {active}}(N(\mathrm {Fin}_*), \mathcal {C})$);
$\mathrm {Fun}_{\mathsf {active}}(N(\mathrm {Fin}_*), \mathcal {C})$);(ii) the induced functor
 $ev_{\langle 1\rangle }\circ F: K\times L^{\rm op}\rightarrow \mathcal {C}$ satisfies that for any square
$ev_{\langle 1\rangle }\circ F: K\times L^{\rm op}\rightarrow \mathcal {C}$ satisfies that for any square  $\alpha : [1]\times [1]^{\rm op}\rightarrow K\times L^{\rm op}$ determined by a functor
$\alpha : [1]\times [1]^{\rm op}\rightarrow K\times L^{\rm op}$ determined by a functor  $\alpha \in \mathrm {Fun}([1],K)\times \mathrm {Fun}([1]^{\rm op},L^{\rm op})$, the diagram
$\alpha \in \mathrm {Fun}([1],K)\times \mathrm {Fun}([1]^{\rm op},L^{\rm op})$, the diagram  $ev_{\langle 1\rangle }\circ F\circ \alpha : [1]\times [1]^{\rm op}\rightarrow \mathcal {C}$ is a Cartesian square;
$ev_{\langle 1\rangle }\circ F\circ \alpha : [1]\times [1]^{\rm op}\rightarrow \mathcal {C}$ is a Cartesian square;
then ![]() $F$ naturally determines a functor
$F$ naturally determines a functor ![]() $F_{\mathrm {CAlg}}: K\times L\rightarrow \mathrm {CAlg}(\mathrm {Corr}(\mathcal {C}^\times ))$.
$F_{\mathrm {CAlg}}: K\times L\rightarrow \mathrm {CAlg}(\mathrm {Corr}(\mathcal {C}^\times ))$.
Proof. Let ![]() $I_{K\times L\times N(\mathrm {Fin}_*)}$ be the coCartesian fibration over
$I_{K\times L\times N(\mathrm {Fin}_*)}$ be the coCartesian fibration over ![]() $N(\Delta )^{\rm op}$ from the Grothendieck construction of
$N(\Delta )^{\rm op}$ from the Grothendieck construction of
Define ![]() $I_K$ and
$I_K$ and ![]() $I_L$ in the same way, and we have
$I_L$ in the same way, and we have
We define a functor
 \begin{align*} & I_{K\times L\times N(\mathrm{Fin}_*)}\underset{I^\mathrm{Comm}}{\times} \mathcal{T}^\mathrm{Comm}\simeq I_K\underset{N(\Delta)^{\rm op}}{\times}I_L\underset{N(\Delta)^{\rm op}}{\times}\mathcal{T}^\mathrm{Comm}\longrightarrow K\times L^{\rm op}\times N(\mathrm{Fin}_*)\\ &([n]; \vartheta^K,\vartheta^L;(s,(i,j),u))\mapsto (\vartheta^K(i),(\vartheta^L)^{\rm op}(j);s^{-1}_{i,j}(u)\sqcup\{*\}). \end{align*}
\begin{align*} & I_{K\times L\times N(\mathrm{Fin}_*)}\underset{I^\mathrm{Comm}}{\times} \mathcal{T}^\mathrm{Comm}\simeq I_K\underset{N(\Delta)^{\rm op}}{\times}I_L\underset{N(\Delta)^{\rm op}}{\times}\mathcal{T}^\mathrm{Comm}\longrightarrow K\times L^{\rm op}\times N(\mathrm{Fin}_*)\\ &([n]; \vartheta^K,\vartheta^L;(s,(i,j),u))\mapsto (\vartheta^K(i),(\vartheta^L)^{\rm op}(j);s^{-1}_{i,j}(u)\sqcup\{*\}). \end{align*}
The composition of the above with ![]() $F$ determines a morphism in
$F$ determines a morphism in ![]() $(1\text {-}\mathcal {C}\mathrm {at})^{\Delta ^{\rm op}}_{/\mathrm {Seq}_\bullet (N(\mathrm {Fin}_*))}$
$(1\text {-}\mathcal {C}\mathrm {at})^{\Delta ^{\rm op}}_{/\mathrm {Seq}_\bullet (N(\mathrm {Fin}_*))}$
To make (2.4.28) into a functor ![]() $K\times L\times N(\mathrm {Fin}_*)\rightarrow \mathrm {Corr}(\mathcal {C})^{\otimes,\mathrm {Fin}_*}$ over
$K\times L\times N(\mathrm {Fin}_*)\rightarrow \mathrm {Corr}(\mathcal {C})^{\otimes,\mathrm {Fin}_*}$ over ![]() $N(\mathrm {Fin}_*)$, we need for every square
$N(\mathrm {Fin}_*)$, we need for every square ![]() $\alpha \in \mathrm {Fun}([1], K)\times \mathrm {Fun}([1]^{\rm op},L^{\rm op})\rightarrow \mathrm {Fun}([1]\times [1]^{\rm op},K\times L^{\rm op})$ in
$\alpha \in \mathrm {Fun}([1], K)\times \mathrm {Fun}([1]^{\rm op},L^{\rm op})\rightarrow \mathrm {Fun}([1]\times [1]^{\rm op},K\times L^{\rm op})$ in ![]() $K\times L^{\rm op}$ and every active morphism
$K\times L^{\rm op}$ and every active morphism ![]() $f: \langle m\rangle \rightarrow \langle n\rangle$ in
$f: \langle m\rangle \rightarrow \langle n\rangle$ in ![]() $N(\mathrm {Fin}_*)$, the following diagram
$N(\mathrm {Fin}_*)$, the following diagram

is Cartesian in ![]() $\mathcal {C}$. Assumption (i) in the proposition reduces the above family of Cartesian diagrams to the following Cartesian diagram
$\mathcal {C}$. Assumption (i) in the proposition reduces the above family of Cartesian diagrams to the following Cartesian diagram

for each ![]() $\alpha$. This is exactly condition (ii) in the proposition and the above determines the desired functor
$\alpha$. This is exactly condition (ii) in the proposition and the above determines the desired functor ![]() $F_\mathrm {CAlg}: K\times L\rightarrow \mathrm {CAlg}(\mathrm {Corr}(\mathcal {C}^\times ))$.
$F_\mathrm {CAlg}: K\times L\rightarrow \mathrm {CAlg}(\mathrm {Corr}(\mathcal {C}^\times ))$.
2.5 Module objects of an algebra object  $C^\bullet$ in
$C^\bullet$ in  $\mathrm {Corr}(\mathcal {C}^\times )$
$\mathrm {Corr}(\mathcal {C}^\times )$
Let ![]() $e: N(\Delta )^{\rm op}\rightarrow N(\Delta )^{\rm op}$ be the natural functor taking
$e: N(\Delta )^{\rm op}\rightarrow N(\Delta )^{\rm op}$ be the natural functor taking ![]() $[n]$ to
$[n]$ to ![]() $[n]\star[0]=[n+1]$, and let
$[n]\star[0]=[n+1]$, and let ![]() $\alpha : e\rightarrow id$ be the obvious natural transformation from
$\alpha : e\rightarrow id$ be the obvious natural transformation from ![]() $e$ to
$e$ to ![]() $id$. These notions have been used in the path space construction for a simplicial space (cf. [Reference SegalSeg74]).
$id$. These notions have been used in the path space construction for a simplicial space (cf. [Reference SegalSeg74]).
Definition 2.20 For any monoidal ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}^{\otimes,\Delta ^{\rm op}}$ over
$\mathcal {C}^{\otimes,\Delta ^{\rm op}}$ over ![]() $N(\Delta )^{\rm op}$, and an algebra object
$N(\Delta )^{\rm op}$, and an algebra object ![]() $C$ defined by a section
$C$ defined by a section ![]() $s\in \mathrm {Hom}_{N(\Delta )^{\rm op}}(N(\Delta )^{\rm op}, \mathcal {C}^\otimes )$, a left
$s\in \mathrm {Hom}_{N(\Delta )^{\rm op}}(N(\Delta )^{\rm op}, \mathcal {C}^\otimes )$, a left ![]() $C$-module
$C$-module ![]() $M$ is given by a functor
$M$ is given by a functor
over ![]() $N(\Delta )^{\rm op}$, where the projection
$N(\Delta )^{\rm op}$, where the projection ![]() $\Delta ^1\times N(\Delta )^{\rm op}\rightarrow N(\Delta ^{\rm op})$ is given by the natural transformation
$\Delta ^1\times N(\Delta )^{\rm op}\rightarrow N(\Delta ^{\rm op})$ is given by the natural transformation ![]() $\theta : e\rightarrow id$, satisfying that:
$\theta : e\rightarrow id$, satisfying that:
(i) it sends every edge
 $\Delta ^1\times \{[k]\}$ to a coCartesian edge in
$\Delta ^1\times \{[k]\}$ to a coCartesian edge in  $\mathcal {C}^{\otimes,\Delta ^{\rm op}}$;
$\mathcal {C}^{\otimes,\Delta ^{\rm op}}$;(ii) the restriction of
 $M$ to
$M$ to  $\{1\}\times N(\Delta )^{\rm op}$ is equivalent to the algebra object
$\{1\}\times N(\Delta )^{\rm op}$ is equivalent to the algebra object  $C$;
$C$;(iii) for any
 $[n]\in N(\Delta )^{\rm op}$, the inclusion
$[n]\in N(\Delta )^{\rm op}$, the inclusion  $\iota _{(0,[j,n])}: (0,[j,n])\hookrightarrow (0,[n])$ in
$\iota _{(0,[j,n])}: (0,[j,n])\hookrightarrow (0,[n])$ in  $N(\Delta )$ is sent to a coCartesian morphism in
$N(\Delta )$ is sent to a coCartesian morphism in  $\mathcal {C}^{\otimes,\Delta ^{\rm op}}$ over
$\mathcal {C}^{\otimes,\Delta ^{\rm op}}$ over  $\alpha (\iota _{(0,[j,n])}^{op }):[0,n+1]\rightarrow [j,n+1]$ in
$\alpha (\iota _{(0,[j,n])}^{op }):[0,n+1]\rightarrow [j,n+1]$ in  $N(\Delta )^{\rm op}$.
$N(\Delta )^{\rm op}$.
Definition 2.21 For any symmetric monoidal ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}^{\otimes, \mathrm {Fin}_*}$ over
$\mathcal {C}^{\otimes, \mathrm {Fin}_*}$ over ![]() $N(\mathrm {Fin}_*)$, and a commutative algebra object
$N(\mathrm {Fin}_*)$, and a commutative algebra object ![]() $C$ given by a section
$C$ given by a section ![]() $s: N(\mathrm {Fin}_*)\rightarrow \mathcal {C}^{\otimes, \mathrm {Fin}_*}$ over
$s: N(\mathrm {Fin}_*)\rightarrow \mathcal {C}^{\otimes, \mathrm {Fin}_*}$ over ![]() $N(\mathrm {Fin}_*)$, a
$N(\mathrm {Fin}_*)$, a ![]() $C$-module
$C$-module ![]() $M$ is defined to be a functor
$M$ is defined to be a functor
over ![]() $N(\mathrm {Fin}_*)$ satisfying that:
$N(\mathrm {Fin}_*)$ satisfying that:
(i) its restriction to the null morphisms from
 $\langle 1\rangle$ (as objects in
$\langle 1\rangle$ (as objects in  $N(\mathrm {Fin}_*)_{\langle 1\rangle /}$) gives
$N(\mathrm {Fin}_*)_{\langle 1\rangle /}$) gives  $C$;
$C$;(ii) it sends every inert morphism to an inert morphism (i.e. coCartesian morphism) in
 $\mathcal {C}^{\otimes, \mathrm {Fin}_*}$.
$\mathcal {C}^{\otimes, \mathrm {Fin}_*}$.
Let ![]() $I_{\Delta ^1\times N(\Delta )^{\rm op}}$ be the 1-category from the Grothendieck construction of the functor
$I_{\Delta ^1\times N(\Delta )^{\rm op}}$ be the 1-category from the Grothendieck construction of the functor ![]() $\mathrm {Seq}_\bullet (\Delta ^1\times N(\Delta )^{\rm op}): N(\Delta )^{\rm op}\rightarrow \mathrm {Sets}$. Let
$\mathrm {Seq}_\bullet (\Delta ^1\times N(\Delta )^{\rm op}): N(\Delta )^{\rm op}\rightarrow \mathrm {Sets}$. Let ![]() $\pi _\theta :I_{\Delta ^1\times N(\Delta )^{\rm op}}\rightarrow I$ be the functor corresponding to
$\pi _\theta :I_{\Delta ^1\times N(\Delta )^{\rm op}}\rightarrow I$ be the functor corresponding to ![]() $\theta : \Delta ^1\times N(\Delta )^{\rm op}\rightarrow N(\Delta )^{\rm op}$ which is a coCartesian fibration by the same argument as in Lemma 2.11.
$\theta : \Delta ^1\times N(\Delta )^{\rm op}\rightarrow N(\Delta )^{\rm op}$ which is a coCartesian fibration by the same argument as in Lemma 2.11.
Given a morphism of simplicial objects ![]() $M^\bullet \rightarrow C^\bullet$ in
$M^\bullet \rightarrow C^\bullet$ in ![]() $\mathcal {C}^\times$, we are aiming to construct a functor
$\mathcal {C}^\times$, we are aiming to construct a functor
over ![]() $I$. We will represent every object in
$I$. We will represent every object in ![]() $I_{\Delta ^1\times N(\Delta ^{\rm op})}$ by
$I_{\Delta ^1\times N(\Delta ^{\rm op})}$ by ![]() $(\alpha, \beta ;\tau )$:
$(\alpha, \beta ;\tau )$:
where, as before, the subscripts indicate the vertices in ![]() $\Delta ^1$ and the arrows indicate the morphisms in
$\Delta ^1$ and the arrows indicate the morphisms in ![]() $(\Delta ^1)^{\rm op}\times N(\Delta )$. The image of
$(\Delta ^1)^{\rm op}\times N(\Delta )$. The image of ![]() $(\alpha, \beta ;\tau )$ in
$(\alpha, \beta ;\tau )$ in ![]() $I$ is
$I$ is
Now we define a functor ![]() $F_{\theta }: I_{\Delta ^1\times N(\Delta )^{\rm op}}\underset {I}{\times } \mathcal {T}\rightarrow \Delta ^1\times N(\Delta )^{\rm op}$ in a similar way as we defined for
$F_{\theta }: I_{\Delta ^1\times N(\Delta )^{\rm op}}\underset {I}{\times } \mathcal {T}\rightarrow \Delta ^1\times N(\Delta )^{\rm op}$ in a similar way as we defined for ![]() $F_{\mathcal {T},\Delta ^{\rm op}}$ in the proof of Theorem 2.8. First, we have the composition
$F_{\mathcal {T},\Delta ^{\rm op}}$ in the proof of Theorem 2.8. First, we have the composition ![]() $\widetilde {F}_\theta : I_{\Delta ^1\times N(\Delta )^{\rm op}}\underset {I}{\times } \mathcal {T}\rightarrow \mathcal {T}\overset {F_{\mathcal {T},N(\Delta )^{\rm op}}}{\rightarrow } N(\Delta )^{\rm op}$. On the object level:
$\widetilde {F}_\theta : I_{\Delta ^1\times N(\Delta )^{\rm op}}\underset {I}{\times } \mathcal {T}\rightarrow \mathcal {T}\overset {F_{\mathcal {T},N(\Delta )^{\rm op}}}{\rightarrow } N(\Delta )^{\rm op}$. On the object level:
(i) for any object
 $(\alpha,\beta,\tau ; (\mu +i,\mu +j), [u,u+1])\in I^\natural _{\Delta ^1\times N(\Delta )^{\rm op}}\underset {I}{\times } \mathcal {T}^\natural$,
$(\alpha,\beta,\tau ; (\mu +i,\mu +j), [u,u+1])\in I^\natural _{\Delta ^1\times N(\Delta )^{\rm op}}\underset {I}{\times } \mathcal {T}^\natural$,  $\widetilde {F}_\theta$ sends it to
$\widetilde {F}_\theta$ sends it to  $[\beta _{ji}(u),\beta _{ji}(u+1)]\in N(\Delta )^{\rm op}$;
$[\beta _{ji}(u),\beta _{ji}(u+1)]\in N(\Delta )^{\rm op}$;(ii) for any object
 $(\alpha,\beta,\tau ; (i,j), [u,u+1])$ with
$(\alpha,\beta,\tau ; (i,j), [u,u+1])$ with  $i,j\leq \mu -1$, if
$i,j\leq \mu -1$, if  $u< n_j$, then
$u< n_j$, then  $F_\theta$ sends it to
$F_\theta$ sends it to  $[\alpha _{ji}(u), \alpha _{ji}(u+1)]$; if
$[\alpha _{ji}(u), \alpha _{ji}(u+1)]$; if  $u=n_j$, then
$u=n_j$, then  $\widetilde {F}_\theta$ sends it to
$\widetilde {F}_\theta$ sends it to  $[\theta (\alpha _{ji})(n_j), n_i+1]$;
$[\theta (\alpha _{ji})(n_j), n_i+1]$;(iii) for any object
 $(\alpha,\beta,\tau ; (i,\mu +j), [u,u+1])$ with
$(\alpha,\beta,\tau ; (i,\mu +j), [u,u+1])$ with  $i\leq \mu -1$,
$i\leq \mu -1$,  $\widetilde {F}_\theta$ sends it to
$\widetilde {F}_\theta$ sends it to
 \[
[\alpha _{\mu -1,i}\tau \beta _{j,0}(u), \alpha _{\mu -1,i}\tau \beta _{j,0}(u+1)].
\]
\[
[\alpha _{\mu -1,i}\tau \beta _{j,0}(u), \alpha _{\mu -1,i}\tau \beta _{j,0}(u+1)].
\]
Now we do the following modification of ![]() $\widetilde {F}_\theta$ on the object level to the above as follows:
$\widetilde {F}_\theta$ on the object level to the above as follows:
(i)
 $[\beta _{ji}(u),\beta _{ji}(u+1)]\in N(\Delta )^{\rm op}\rightsquigarrow (1, [\beta _{ji}(u),\beta _{ji}(u+1)])\in \Delta ^1\times N(\Delta )^{\rm op}$;
$[\beta _{ji}(u),\beta _{ji}(u+1)]\in N(\Delta )^{\rm op}\rightsquigarrow (1, [\beta _{ji}(u),\beta _{ji}(u+1)])\in \Delta ^1\times N(\Delta )^{\rm op}$;(ii) if
 $u< n_j$,
$u< n_j$,  $[\alpha _{ji}(u), \alpha _{ji}(u+1)]\in N(\Delta )^{\rm op}\rightsquigarrow$
$[\alpha _{ji}(u), \alpha _{ji}(u+1)]\in N(\Delta )^{\rm op}\rightsquigarrow$  $[(1, [\alpha _{ji}(u), \alpha _{ji}(u+1)])\in \Delta ^1\times N(\Delta )^{\rm op}$; if
$[(1, [\alpha _{ji}(u), \alpha _{ji}(u+1)])\in \Delta ^1\times N(\Delta )^{\rm op}$; if  $u=n_j$, then
$u=n_j$, then  $[\theta (\alpha _{ji})(n_j), n_i+1]\in N(\Delta )^{\rm op}\rightsquigarrow$
$[\theta (\alpha _{ji})(n_j), n_i+1]\in N(\Delta )^{\rm op}\rightsquigarrow$  $[(0, [\theta (\alpha _{ji})(n_j), n_i])=(0, [\alpha _{ji}(n_j), n_i])\in \Delta ^1\times N(\Delta )^{\rm op}$;
$[(0, [\theta (\alpha _{ji})(n_j), n_i])=(0, [\alpha _{ji}(n_j), n_i])\in \Delta ^1\times N(\Delta )^{\rm op}$;(iii)
 $[\alpha _{\mu -1,i}\tau \beta _{j,0}(u), \alpha _{\mu -1,i}\tau \beta _{j,0}(u+1)]\!\in\! N(\Delta )^{\rm op}\rightsquigarrow$
$[\alpha _{\mu -1,i}\tau \beta _{j,0}(u), \alpha _{\mu -1,i}\tau \beta _{j,0}(u+1)]\!\in\! N(\Delta )^{\rm op}\rightsquigarrow$  $[(1, [\alpha _{\mu -1,i}\tau \beta _{j,0}(u), \alpha _{\mu -1,i}\tau \beta _{j,0}(u+1)])\in \Delta ^1\times N(\Delta )^{\rm op}$.
$[(1, [\alpha _{\mu -1,i}\tau \beta _{j,0}(u), \alpha _{\mu -1,i}\tau \beta _{j,0}(u+1)])\in \Delta ^1\times N(\Delta )^{\rm op}$.
Since ![]() $\theta (\alpha _{ji})$ maps
$\theta (\alpha _{ji})$ maps ![]() $n_{j}+1$ to
$n_{j}+1$ to ![]() $n_i+1$ and
$n_i+1$ and ![]() $n_j$ to a number less than or equal to
$n_j$ to a number less than or equal to ![]() $n_i$, it is easy to see that the above modification defines a functor
$n_i$, it is easy to see that the above modification defines a functor ![]() $I_{\Delta ^1\times N(\Delta )^{\rm op}}\underset {I}{\times } \mathcal {T}\rightarrow \Delta ^1\times N(\Delta )^{\rm op}$ and that is
$I_{\Delta ^1\times N(\Delta )^{\rm op}}\underset {I}{\times } \mathcal {T}\rightarrow \Delta ^1\times N(\Delta )^{\rm op}$ and that is ![]() $F_\theta$.
$F_\theta$.
Now viewing ![]() $M^\bullet \rightarrow C^\bullet$ as a functor
$M^\bullet \rightarrow C^\bullet$ as a functor ![]() $MC: \Delta ^1\times N(\Delta )^{\rm op}\rightarrow \mathcal {C}$, the composition
$MC: \Delta ^1\times N(\Delta )^{\rm op}\rightarrow \mathcal {C}$, the composition ![]() $MC\circ F_\theta$ gives the functor
$MC\circ F_\theta$ gives the functor ![]() $F_{M,C}$ (2.5.1).
$F_{M,C}$ (2.5.1).
Theorem 2.22 Given a morphism of simplicial objects ![]() $M^\bullet \rightarrow C^\bullet$ in
$M^\bullet \rightarrow C^\bullet$ in ![]() $\mathcal {C}^\times$, if
$\mathcal {C}^\times$, if ![]() $C^\bullet$ represents an algebra object in
$C^\bullet$ represents an algebra object in ![]() $\mathrm {Corr}(\mathcal {C})$, i.e. it satisfies the conditions in Theorem 2.8(i), and
$\mathrm {Corr}(\mathcal {C})$, i.e. it satisfies the conditions in Theorem 2.8(i), and ![]() $M^\bullet$ satisfies that for any morphism
$M^\bullet$ satisfies that for any morphism ![]() $f: [m]\rightarrow [n]$ in
$f: [m]\rightarrow [n]$ in ![]() $N(\Delta )$, we have that the diagram
$N(\Delta )$, we have that the diagram

is Cartesian in ![]() $\mathcal {C}$, then the data naturally determine a left module of
$\mathcal {C}$, then the data naturally determine a left module of ![]() $C$ in
$C$ in ![]() $\mathrm {Corr}(\mathcal {C})$. Moreover, the condition on
$\mathrm {Corr}(\mathcal {C})$. Moreover, the condition on ![]() $M^\bullet$ is both necessary and sufficient.
$M^\bullet$ is both necessary and sufficient.
Proof. Assuming ![]() $C^\bullet$ gives an algebra object in
$C^\bullet$ gives an algebra object in ![]() $\mathrm {Corr}(\mathcal {C})$, to make
$\mathrm {Corr}(\mathcal {C})$, to make ![]() $F_{M,C}$ a functor from
$F_{M,C}$ a functor from ![]() $\Delta ^1\times N(\Delta )^{\rm op}$ to
$\Delta ^1\times N(\Delta )^{\rm op}$ to ![]() $\mathrm {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}$, we need for every object
$\mathrm {Corr}(\mathcal {C})^{\otimes, \Delta ^{\rm op}}$, we need for every object ![]() $(\alpha,\beta ;\tau )$ in
$(\alpha,\beta ;\tau )$ in ![]() $I_{\Delta ^1\times N(\Delta )^{\rm op}}$ and any
$I_{\Delta ^1\times N(\Delta )^{\rm op}}$ and any ![]() $i\leq j\leq \mu -1$, the diagram
$i\leq j\leq \mu -1$, the diagram

is Cartesian in ![]() $\mathcal {C}$. But this is exactly the condition that (2.5.2) is Cartesian in
$\mathcal {C}$. But this is exactly the condition that (2.5.2) is Cartesian in ![]() $\mathcal {C}$. By construction,
$\mathcal {C}$. By construction, ![]() $F_{M,C}$ certainly satisfies condition (ii) in Definition 2.20. Conditions (i) and (iii) can be easily checked by the characterization of a 2-coCartesian morphism in
$F_{M,C}$ certainly satisfies condition (ii) in Definition 2.20. Conditions (i) and (iii) can be easily checked by the characterization of a 2-coCartesian morphism in ![]() $\mathrm {Corr}(\mathcal {C})^{\otimes,\Delta ^{\rm op}}$ at the beginning of the proof of Proposition 2.1 and the characterization of a Cartesian morphism in
$\mathrm {Corr}(\mathcal {C})^{\otimes,\Delta ^{\rm op}}$ at the beginning of the proof of Proposition 2.1 and the characterization of a Cartesian morphism in ![]() $\mathcal {C}^{\times, \Delta }$ in Proposition 2.5.
$\mathcal {C}^{\times, \Delta }$ in Proposition 2.5.
In a similar fashion, for the commutative case, introduce ![]() $\mathrm {Fin}_{*,{\dagger} }$ to be the ordinary 1-category consisting of
$\mathrm {Fin}_{*,{\dagger} }$ to be the ordinary 1-category consisting of ![]() $\langle n\rangle _{\dagger} := \langle n\rangle \sqcup \{{\dagger} \}$, and morphisms
$\langle n\rangle _{\dagger} := \langle n\rangle \sqcup \{{\dagger} \}$, and morphisms ![]() $\langle n\rangle _{\dagger} \rightarrow \langle m\rangle _{\dagger}$ being maps of sets that send
$\langle n\rangle _{\dagger} \rightarrow \langle m\rangle _{\dagger}$ being maps of sets that send ![]() $*$ to
$*$ to ![]() $*$ and
$*$ and ![]() ${\dagger}$ to
${\dagger}$ to ![]() ${\dagger}$. Note that there is a natural functor
${\dagger}$. Note that there is a natural functor ![]() $\pi _{\dagger} : N(\mathrm {Fin}_{*,{\dagger} })\rightarrow N(\mathrm {Fin}_*)$ that sends
$\pi _{\dagger} : N(\mathrm {Fin}_{*,{\dagger} })\rightarrow N(\mathrm {Fin}_*)$ that sends ![]() $\langle n\rangle _{\dagger}$ to
$\langle n\rangle _{\dagger}$ to ![]() $\langle n\rangle$, and sends
$\langle n\rangle$, and sends ![]() $f: \langle n\rangle _{\dagger} \rightarrow \langle m\rangle _{\dagger}$ to
$f: \langle n\rangle _{\dagger} \rightarrow \langle m\rangle _{\dagger}$ to ![]() $\widetilde {f}: \langle n\rangle \rightarrow \langle m\rangle$ where
$\widetilde {f}: \langle n\rangle \rightarrow \langle m\rangle$ where ![]() $\widetilde {f}$ sends
$\widetilde {f}$ sends ![]() $f^{-1}(\{{\dagger},*\})\backslash \{{\dagger} \}$ to
$f^{-1}(\{{\dagger},*\})\backslash \{{\dagger} \}$ to ![]() $*$ and others in the same way as
$*$ and others in the same way as ![]() $f$. Let
$f$. Let ![]() $I_{\pi _{\dagger} }$ be the Grothendieck construction of
$I_{\pi _{\dagger} }$ be the Grothendieck construction of ![]() $\pi _{\dagger} : \Delta ^1\rightarrow 1\text {-}\mathcal {C}\mathrm {at}^\mathrm {ord}$. We will denote each object in
$\pi _{\dagger} : \Delta ^1\rightarrow 1\text {-}\mathcal {C}\mathrm {at}^\mathrm {ord}$. We will denote each object in ![]() $I_{\pi _{\dagger} }$ by
$I_{\pi _{\dagger} }$ by ![]() $(0,\langle n\rangle _{\dagger} )$ or
$(0,\langle n\rangle _{\dagger} )$ or ![]() $(1, \langle n\rangle )$ if it projects to 0 or 1 in
$(1, \langle n\rangle )$ if it projects to 0 or 1 in ![]() $\Delta ^1$, respectively. Note that there is a natural equivalence
$\Delta ^1$, respectively. Note that there is a natural equivalence ![]() $N(\mathrm {Fin}_*)_{\langle 1\rangle /}\rightarrow I_{\pi _{\dagger} }$ that takes the object
$N(\mathrm {Fin}_*)_{\langle 1\rangle /}\rightarrow I_{\pi _{\dagger} }$ that takes the object ![]() $b: \langle 1\rangle \rightarrow \langle m\rangle$ to
$b: \langle 1\rangle \rightarrow \langle m\rangle$ to ![]() $(1,\langle m\rangle )$ if
$(1,\langle m\rangle )$ if ![]() $b$ is null and to
$b$ is null and to ![]() $(0, \langle m-1\rangle _{\dagger} )$ otherwise.
$(0, \langle m-1\rangle _{\dagger} )$ otherwise.
We will define a natural functor ![]() $F_\theta ^\mathrm {Comm}: I_{N(\mathrm {Fin}_*)_{\langle 1\rangle /}}\underset {I^\mathrm {Comm}}{\times } \mathcal {T}^\mathrm {Comm}\rightarrow I_{\pi _{\dagger} }$ as follows, where the functor
$F_\theta ^\mathrm {Comm}: I_{N(\mathrm {Fin}_*)_{\langle 1\rangle /}}\underset {I^\mathrm {Comm}}{\times } \mathcal {T}^\mathrm {Comm}\rightarrow I_{\pi _{\dagger} }$ as follows, where the functor ![]() $N(\mathrm {Fin}_{*})_{\langle 1\rangle /}\rightarrow N(\mathrm {Fin}_*)$ is the natural projection. First, we have the composition functor
$N(\mathrm {Fin}_{*})_{\langle 1\rangle /}\rightarrow N(\mathrm {Fin}_*)$ is the natural projection. First, we have the composition functor
We denote every object in ![]() $I_{N(\mathrm {Fin}_*)_{\langle 1\rangle /}}$ by
$I_{N(\mathrm {Fin}_*)_{\langle 1\rangle /}}$ by ![]() $(\alpha,\beta ;\tau )$ represented by
$(\alpha,\beta ;\tau )$ represented by

where the morphism ![]() $\langle 1\rangle \rightarrow \langle \bullet \rangle _\epsilon$ is null if and only if
$\langle 1\rangle \rightarrow \langle \bullet \rangle _\epsilon$ is null if and only if ![]() $\epsilon =1$. We will abuse notation and denote the image of
$\epsilon =1$. We will abuse notation and denote the image of ![]() $(\alpha,\beta,\tau )$ in
$(\alpha,\beta,\tau )$ in ![]() $I^{\mathrm {Comm}}$ under the obvious projection by the same notation. On the object level:
$I^{\mathrm {Comm}}$ under the obvious projection by the same notation. On the object level:
(i) for any object
 $(\alpha,\beta,\tau ; (\mu +i,\mu +j), t)\in I_{N(\mathrm {Fin}_*)_{\langle 1\rangle /}}\underset {I^\mathrm {Comm}}{\times } \mathcal {T}^\mathrm {Comm}$, for
$(\alpha,\beta,\tau ; (\mu +i,\mu +j), t)\in I_{N(\mathrm {Fin}_*)_{\langle 1\rangle /}}\underset {I^\mathrm {Comm}}{\times } \mathcal {T}^\mathrm {Comm}$, for  $0\leq i\leq j\leq k-\mu$,
$0\leq i\leq j\leq k-\mu$,  $\widetilde {F}_\theta ^\mathrm {Comm}$ sends it to
$\widetilde {F}_\theta ^\mathrm {Comm}$ sends it to  $\beta _{ij}^{-1}(t)\sqcup \{*\}$;
$\beta _{ij}^{-1}(t)\sqcup \{*\}$;(ii) for any object
 $(\alpha,\beta,\tau ; (i,j), t)$,
$(\alpha,\beta,\tau ; (i,j), t)$,  $0\leq i\leq j\leq \mu -1$,
$0\leq i\leq j\leq \mu -1$,  $\widetilde {F}_\theta ^\mathrm {Comm}$ sends it to
$\widetilde {F}_\theta ^\mathrm {Comm}$ sends it to  $\alpha _{ij}^{-1}(t)\sqcup \{*\}$;
$\alpha _{ij}^{-1}(t)\sqcup \{*\}$;(iii) for any object
 $(\alpha,\beta,\tau ; (i,\mu +j), t)$, for
$(\alpha,\beta,\tau ; (i,\mu +j), t)$, for  $0\leq i\leq \mu -1$,
$0\leq i\leq \mu -1$,  $\widetilde {F}_\theta ^\mathrm {Comm}$ sends it to
$\widetilde {F}_\theta ^\mathrm {Comm}$ sends it to  $(\beta _{0j}\tau \alpha _{i,\mu -1})^{-1}(t) \sqcup \{*\}$.
$(\beta _{0j}\tau \alpha _{i,\mu -1})^{-1}(t) \sqcup \{*\}$.
We will modify ![]() $\widetilde {F}_\theta ^\mathrm {Comm}$ on the object level in each of the above cases:
$\widetilde {F}_\theta ^\mathrm {Comm}$ on the object level in each of the above cases:
(i)
 $\beta _{ij}^{-1}(t)\sqcup \{*\}\rightsquigarrow (1,\beta _{ij}^{-1}(t)\sqcup \{*\})\in I_{\pi _{\dagger} }$;
$\beta _{ij}^{-1}(t)\sqcup \{*\}\rightsquigarrow (1,\beta _{ij}^{-1}(t)\sqcup \{*\})\in I_{\pi _{\dagger} }$;(ii) if
 $t$ is the image of
$t$ is the image of  $1\in \langle 1\rangle$, then
$1\in \langle 1\rangle$, then  $\alpha _{ij}^{-1}(t)\sqcup \{*\}\rightsquigarrow (0,(\alpha _{ij}^{-1}(t)\backslash (\alpha _{0i}\gamma _0)(1))\sqcup \{{\dagger}, *\})\in I_{\pi _{\dagger} }$, i.e. we replace
$\alpha _{ij}^{-1}(t)\sqcup \{*\}\rightsquigarrow (0,(\alpha _{ij}^{-1}(t)\backslash (\alpha _{0i}\gamma _0)(1))\sqcup \{{\dagger}, *\})\in I_{\pi _{\dagger} }$, i.e. we replace  $\alpha _{0i}\gamma _0(1)$ by
$\alpha _{0i}\gamma _0(1)$ by  ${\dagger}$; if
${\dagger}$; if  $t$ is not in the image of
$t$ is not in the image of  $1\in \langle 1\rangle$, then
$1\in \langle 1\rangle$, then  $\alpha _{ij}^{-1}(t)\sqcup \{*\}\rightsquigarrow (1, \alpha _{ij}^{-1}(t) \sqcup \{*\})$;
$\alpha _{ij}^{-1}(t)\sqcup \{*\}\rightsquigarrow (1, \alpha _{ij}^{-1}(t) \sqcup \{*\})$;(iii)
 $(\beta _{0j}\tau \alpha _{i,\mu -1})^{-1}(t)\sqcup \{*\}\rightsquigarrow (1,(\beta _{0j}\tau \alpha _{i,\mu -1})^{-1}(t)\sqcup \{*\})$.
$(\beta _{0j}\tau \alpha _{i,\mu -1})^{-1}(t)\sqcup \{*\}\rightsquigarrow (1,(\beta _{0j}\tau \alpha _{i,\mu -1})^{-1}(t)\sqcup \{*\})$.
This modification uniquely determines a functor ![]() $F_\theta ^\mathrm {Comm}: I_{N(\mathrm {Fin}_*)_{\langle 1\rangle /}}\underset {I^\mathrm {Comm}}{\times } (\mathcal {T}^\mathrm {Comm})\rightarrow I_{\pi _{\dagger} }$: if we think of the coCartesian morphism
$F_\theta ^\mathrm {Comm}: I_{N(\mathrm {Fin}_*)_{\langle 1\rangle /}}\underset {I^\mathrm {Comm}}{\times } (\mathcal {T}^\mathrm {Comm})\rightarrow I_{\pi _{\dagger} }$: if we think of the coCartesian morphism ![]() $(0,\langle n\rangle _{\dagger} )\rightarrow (1,\langle n\rangle )$ in
$(0,\langle n\rangle _{\dagger} )\rightarrow (1,\langle n\rangle )$ in ![]() $I_{\pi _{\dagger} }$ as an inert morphism sending
$I_{\pi _{\dagger} }$ as an inert morphism sending ![]() ${\dagger}$ to
${\dagger}$ to ![]() $*$, then the modification of
$*$, then the modification of ![]() $\widetilde {F}_{\theta }^\mathrm {Comm}$ is just replacing the image of
$\widetilde {F}_{\theta }^\mathrm {Comm}$ is just replacing the image of ![]() $1\in \langle 1\rangle$ in each
$1\in \langle 1\rangle$ in each ![]() $\langle n_i\rangle _0$ (and its subsets containing the image) by
$\langle n_i\rangle _0$ (and its subsets containing the image) by ![]() ${\dagger}$ and mark it with
${\dagger}$ and mark it with ![]() $0\in \Delta ^1$; since
$0\in \Delta ^1$; since ![]() ${\dagger}$ can be only mapped to
${\dagger}$ can be only mapped to ![]() ${\dagger}$ or
${\dagger}$ or ![]() $*$, whose projection to
$*$, whose projection to ![]() $\Delta ^1$ is
$\Delta ^1$ is ![]() $id_{0}$ and
$id_{0}$ and ![]() $0\rightarrow 1$, respectively,
$0\rightarrow 1$, respectively, ![]() $F_\theta ^\mathrm {Comm}$ is well defined.
$F_\theta ^\mathrm {Comm}$ is well defined.
Given a diagram

and a natural transformation ![]() $\eta : M^{\bullet,{\dagger} }\rightarrow C^\bullet \circ \pi _{\dagger}$, which we can view as a functor
$\eta : M^{\bullet,{\dagger} }\rightarrow C^\bullet \circ \pi _{\dagger}$, which we can view as a functor ![]() $MC^\mathrm {Comm}:I_{\pi _{\dagger} }\rightarrow \mathcal {C}$, the composition
$MC^\mathrm {Comm}:I_{\pi _{\dagger} }\rightarrow \mathcal {C}$, the composition ![]() $MC^\mathrm {Comm}\circ F_\theta ^\mathrm {Comm}$ induces a functor between coCartesian fibrations
$MC^\mathrm {Comm}\circ F_\theta ^\mathrm {Comm}$ induces a functor between coCartesian fibrations
over ![]() $I^\mathrm {Comm}$.
$I^\mathrm {Comm}$.
Theorem 2.23 Assume we are given a ![]() $\mathrm {Fin}_{*,{\dagger} }$-object
$\mathrm {Fin}_{*,{\dagger} }$-object ![]() $M^{\bullet,{\dagger} }$ and a
$M^{\bullet,{\dagger} }$ and a ![]() $\mathrm {Fin}_*$-object
$\mathrm {Fin}_*$-object ![]() $C^\bullet$ in
$C^\bullet$ in ![]() $\mathcal {C}^\times$, together with a natural transformation
$\mathcal {C}^\times$, together with a natural transformation ![]() $\eta : M^{\bullet,{\dagger} }\rightarrow C^\bullet \circ \pi _{\dagger}$. If
$\eta : M^{\bullet,{\dagger} }\rightarrow C^\bullet \circ \pi _{\dagger}$. If ![]() $C^\bullet$ represents a commutative algebra object in
$C^\bullet$ represents a commutative algebra object in ![]() $\mathrm {Corr}(\mathcal {C})$, i.e. it satisfies the conditions in Theorem 2.8(ii), and
$\mathrm {Corr}(\mathcal {C})$, i.e. it satisfies the conditions in Theorem 2.8(ii), and ![]() $M^{\bullet,{\dagger} }$ satisfies that for any active morphism
$M^{\bullet,{\dagger} }$ satisfies that for any active morphism ![]() $f: \langle n\rangle _{\dagger} \rightarrow \langle m\rangle _{\dagger}$, i.e.
$f: \langle n\rangle _{\dagger} \rightarrow \langle m\rangle _{\dagger}$, i.e. ![]() $f^{-1}(*)=*$, we have that the diagram
$f^{-1}(*)=*$, we have that the diagram

is Cartesian in ![]() $\mathcal {C}$, then the data naturally determine a module of
$\mathcal {C}$, then the data naturally determine a module of ![]() $C$ in
$C$ in ![]() $\mathrm {Corr}(\mathcal {C})$. Moreover, the condition on
$\mathrm {Corr}(\mathcal {C})$. Moreover, the condition on ![]() $M^{\bullet,{\dagger} }$ is both necessary and sufficient.
$M^{\bullet,{\dagger} }$ is both necessary and sufficient.
Proof. The proof is completely similar to that of Theorem 2.22. For any object ![]() $(\alpha,\beta,\tau )\in I_{N(\mathrm {Fin}_*)_{\langle 1\rangle /}}$, we just need to make sure that for any
$(\alpha,\beta,\tau )\in I_{N(\mathrm {Fin}_*)_{\langle 1\rangle /}}$, we just need to make sure that for any ![]() $t=\alpha _{0j}\gamma _0(1)$, the diagram
$t=\alpha _{0j}\gamma _0(1)$, the diagram

is Cartesian in ![]() $\mathcal {C}$.
$\mathcal {C}$.
The condition is equivalent to that for any morphism ![]() $f: \langle n\rangle \rightarrow \langle m\rangle$ and any
$f: \langle n\rangle \rightarrow \langle m\rangle$ and any ![]() $a\in \langle n\rangle ^\circ$ such that
$a\in \langle n\rangle ^\circ$ such that ![]() $f(a)\neq *$ in
$f(a)\neq *$ in ![]() $N(\mathrm {Fin}_*)$, we have the following diagram
$N(\mathrm {Fin}_*)$, we have the following diagram

is Cartesian in ![]() $\mathcal {C}$. This is equivalent to (2.5.4)
$\mathcal {C}$. This is equivalent to (2.5.4)
Recall the definition of
given in [Reference LurieLur17, Definition 3.3.3.8] for any map ![]() $\mathcal {C}^{\otimes }\rightarrow \mathcal {O}^{\otimes }$ of generalized
$\mathcal {C}^{\otimes }\rightarrow \mathcal {O}^{\otimes }$ of generalized ![]() $\infty$-operads. For
$\infty$-operads. For ![]() $\mathcal {O}^\otimes =N(\mathrm {Fin}_*)$, we use
$\mathcal {O}^\otimes =N(\mathrm {Fin}_*)$, we use ![]() $\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {C})$ to denote the fiber product
$\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {C})$ to denote the fiber product
and any object is represented by a pair ![]() $(A,M)$, where
$(A,M)$, where ![]() $A$ is a commutative algebra object in
$A$ is a commutative algebra object in ![]() $\mathcal {C}$ and
$\mathcal {C}$ and ![]() $M$ is an
$M$ is an ![]() $A$-module. In the following, we represent every object
$A$-module. In the following, we represent every object ![]() $(\langle 1\rangle \rightarrow \langle n\rangle )$ in
$(\langle 1\rangle \rightarrow \langle n\rangle )$ in ![]() $N(\mathrm {Fin}_*)_{\langle 1\rangle /}$ by a pair
$N(\mathrm {Fin}_*)_{\langle 1\rangle /}$ by a pair ![]() $(\langle n\rangle, s)$, where
$(\langle n\rangle, s)$, where ![]() $s\in \langle n\rangle$ is the image of
$s\in \langle n\rangle$ is the image of ![]() $1\in \langle 1\rangle$ and is regarded as the marking.
$1\in \langle 1\rangle$ and is regarded as the marking.
When ![]() $\mathcal {C}^{\otimes }=(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})^{\otimes }$, any object in
$\mathcal {C}^{\otimes }=(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})^{\otimes }$, any object in ![]() $\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$ can be represented by a coCartesian fibration
$\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$ can be represented by a coCartesian fibration
satisfying that:
(i) the pullback of (2.5.7) along the inclusion of null morphisms
 $N(\mathrm {Fin}_*)\hookrightarrow N(\mathrm {Fin}_*)_{\langle 1\rangle /}$ gives a coCartsian fibration
$N(\mathrm {Fin}_*)\hookrightarrow N(\mathrm {Fin}_*)_{\langle 1\rangle /}$ gives a coCartsian fibration  $C^\otimes \rightarrow N(\mathrm {Fin}_*)$ that represents a symmetric monoidal stable
$C^\otimes \rightarrow N(\mathrm {Fin}_*)$ that represents a symmetric monoidal stable  $\infty$-category
$\infty$-category  $C\simeq \mathcal {M}_{(\langle 1\rangle, *)}$;
$C\simeq \mathcal {M}_{(\langle 1\rangle, *)}$;(ii) for any object
 $(\langle n\rangle, s)\in N(\mathrm {Fin}_*)_{\langle 1\rangle /}$, the coCartesian morphisms over the
$(\langle n\rangle, s)\in N(\mathrm {Fin}_*)_{\langle 1\rangle /}$, the coCartesian morphisms over the  $n$ inert morphisms
$n$ inert morphisms  $\rho ^i: (\langle n\rangle, s)\rightarrow (\langle 1\rangle,\rho ^i(s))$ gives an equivalence
(2.5.8)of
$\rho ^i: (\langle n\rangle, s)\rightarrow (\langle 1\rangle,\rho ^i(s))$ gives an equivalence
(2.5.8)of \begin{equation} \mathcal{M}_{(\langle n\rangle, s)}\overset{\sim}{\rightarrow} \prod_{i=1}^n \mathcal{M}_{(\langle 1\rangle, \rho^i(s))} \end{equation}
\begin{equation} \mathcal{M}_{(\langle n\rangle, s)}\overset{\sim}{\rightarrow} \prod_{i=1}^n \mathcal{M}_{(\langle 1\rangle, \rho^i(s))} \end{equation} $\infty$-categories;
$\infty$-categories;(iii) the fiber
 $\mathcal {M}_{(\langle 1\rangle, 1)}$ is stable, and any morphism in
$\mathcal {M}_{(\langle 1\rangle, 1)}$ is stable, and any morphism in  $\mathcal {M}$ over
$\mathcal {M}$ over  $\alpha : (\langle m\rangle,s)\rightarrow (\langle n\rangle, \alpha (s))$, given by
$\alpha : (\langle m\rangle,s)\rightarrow (\langle n\rangle, \alpha (s))$, given by  $n$ functors via (2.5.8),
satisfies that each
$n$ functors via (2.5.8),
satisfies that each \[ F_i: \prod_{j\in \alpha^{-1}(i)} \mathcal{M}_{(\langle 1\rangle, \rho^i(s))}\rightarrow \mathcal{M}_{(\langle 1\rangle, \rho^i\alpha(s))},\ i\in \langle n\rangle^\circ, \]
\[ F_i: \prod_{j\in \alpha^{-1}(i)} \mathcal{M}_{(\langle 1\rangle, \rho^i(s))}\rightarrow \mathcal{M}_{(\langle 1\rangle, \rho^i\alpha(s))},\ i\in \langle n\rangle^\circ, \]
 $F_i$ is exact and continuous in each variable.
$F_i$ is exact and continuous in each variable.
Moreover, a right-lax morphism (respectively, morphism) between two objects ![]() $\mathcal {M}\rightarrow N(\mathrm {Fin}_*)_{\langle 1\rangle /}$ and
$\mathcal {M}\rightarrow N(\mathrm {Fin}_*)_{\langle 1\rangle /}$ and ![]() $\mathcal {N}\rightarrow N(\mathrm {Fin}_*)_{\langle 1\rangle /}$ in
$\mathcal {N}\rightarrow N(\mathrm {Fin}_*)_{\langle 1\rangle /}$ in ![]() $\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$ is given by a commutative diagram
$\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$ is given by a commutative diagram

that restricts to exact and continuous functors ![]() $\mathcal {M}_{(\langle 1\rangle, 1)}\rightarrow \mathcal {N}_{(\langle 1\rangle, 1)}$ and
$\mathcal {M}_{(\langle 1\rangle, 1)}\rightarrow \mathcal {N}_{(\langle 1\rangle, 1)}$ and ![]() $\mathcal {M}_{(\langle 1\rangle,*)}\rightarrow \mathcal {N}_{(\langle 1\rangle,*)}$ and that sends coCartesian morphisms in
$\mathcal {M}_{(\langle 1\rangle,*)}\rightarrow \mathcal {N}_{(\langle 1\rangle,*)}$ and that sends coCartesian morphisms in ![]() $\mathcal {M}$ over inert morphisms (respectively, all morphisms) in
$\mathcal {M}$ over inert morphisms (respectively, all morphisms) in ![]() $N(\mathrm {Fin}_*)_{\langle 1\rangle /}$ to coCartesian morphisms in
$N(\mathrm {Fin}_*)_{\langle 1\rangle /}$ to coCartesian morphisms in ![]() $\mathcal {N}$.
$\mathcal {N}$.
Given two pairs ![]() $(C^\bullet, M^{\bullet,{\dagger} })$,
$(C^\bullet, M^{\bullet,{\dagger} })$, ![]() $(D^\bullet, N^{\bullet,{\dagger} })$ of a module over a commutative algebra in
$(D^\bullet, N^{\bullet,{\dagger} })$ of a module over a commutative algebra in ![]() $\mathbf {Corr}(\mathcal {C}^\times )$, similarly to the construction of (right-lax) algebra homomorphisms in
$\mathbf {Corr}(\mathcal {C}^\times )$, similarly to the construction of (right-lax) algebra homomorphisms in ![]() $\mathbf {Corr}(\mathcal {C}^\times )$, we can construct a (right-lax) morphism between the two pairs in the sense of [Reference Gaitsgory and RozenblyumGR17, Chapter 8, 3.5.1] from a correspondence
$\mathbf {Corr}(\mathcal {C}^\times )$, we can construct a (right-lax) morphism between the two pairs in the sense of [Reference Gaitsgory and RozenblyumGR17, Chapter 8, 3.5.1] from a correspondence

of modules over commutative algebras. Let ![]() $I_{\widetilde {\pi }_{{\dagger} }}$ be the ordinary 1-category from the Grothendieck construction of the functor
$I_{\widetilde {\pi }_{{\dagger} }}$ be the ordinary 1-category from the Grothendieck construction of the functor
 \[ \widetilde{\pi}_{{\dagger}}: N(\mathrm{Fin}_{*,{\dagger}})\times \bigg(\Delta^{\{W,M\}}\coprod_{\Delta^{\{W\}}}\Delta^{\{W,N\}}\bigg)\rightarrow N(\mathrm{Fin}_{*})\times \bigg(\Delta^{\{P,C\}}\coprod_{\Delta^{\{P\}}}\Delta^{\{P,D\}}\bigg), \]
\[ \widetilde{\pi}_{{\dagger}}: N(\mathrm{Fin}_{*,{\dagger}})\times \bigg(\Delta^{\{W,M\}}\coprod_{\Delta^{\{W\}}}\Delta^{\{W,N\}}\bigg)\rightarrow N(\mathrm{Fin}_{*})\times \bigg(\Delta^{\{P,C\}}\coprod_{\Delta^{\{P\}}}\Delta^{\{P,D\}}\bigg), \]
which is given by ![]() $(\pi _{\dagger},(W\mapsto P, M\mapsto C, N\mapsto D))$. We can regard (
$(\pi _{\dagger},(W\mapsto P, M\mapsto C, N\mapsto D))$. We can regard (
) as a functor
Now we are going to construct a functor
First, we have the composite functor
 \begin{align*} &\widetilde{F}_{\theta,
\mathrm{module}}^{\mathrm{Comm}}:
I_{N(\mathrm{Fin}_*)_{\langle
1\rangle/}{\bigcirc{\kern-6pt \star}}
\Delta^1}\underset{I_+^\mathrm{Comm}}{\times}
\mathcal{T}_+^\mathrm{Comm}\rightarrow
I_{N(\mathrm{Fin}_*){\bigcirc{\kern-6pt \star}}
\Delta^1}\underset{I_+^\mathrm{Comm}}{\times}
\mathcal{T}_+^\mathrm{Comm}\\ &\qquad\qquad \rightarrow
N(\mathrm{Fin}_*)\times
\bigg(\Delta^{\{W,M\}}\coprod_{\Delta^{\{W\}}}\Delta^{\{W,N\}}\bigg),
\end{align*}
\begin{align*} &\widetilde{F}_{\theta,
\mathrm{module}}^{\mathrm{Comm}}:
I_{N(\mathrm{Fin}_*)_{\langle
1\rangle/}{\bigcirc{\kern-6pt \star}}
\Delta^1}\underset{I_+^\mathrm{Comm}}{\times}
\mathcal{T}_+^\mathrm{Comm}\rightarrow
I_{N(\mathrm{Fin}_*){\bigcirc{\kern-6pt \star}}
\Delta^1}\underset{I_+^\mathrm{Comm}}{\times}
\mathcal{T}_+^\mathrm{Comm}\\ &\qquad\qquad \rightarrow
N(\mathrm{Fin}_*)\times
\bigg(\Delta^{\{W,M\}}\coprod_{\Delta^{\{W\}}}\Delta^{\{W,N\}}\bigg),
\end{align*}
in which the first functor comes from the projection ![]() $N(\mathrm {Fin}_*)_{\langle 1\rangle /}\rightarrow N(\mathrm {Fin}_*)$ and the second functor is the commutative version of
$N(\mathrm {Fin}_*)_{\langle 1\rangle /}\rightarrow N(\mathrm {Fin}_*)$ and the second functor is the commutative version of ![]() $F_{{\bigcirc{\kern-6pt \star}}, \mathcal {T}_+}$ defined in § 2.4.1 (note that we have changed
$F_{{\bigcirc{\kern-6pt \star}}, \mathcal {T}_+}$ defined in § 2.4.1 (note that we have changed ![]() $C,D$ to
$C,D$ to ![]() $M,N$ respectively in the target).
$M,N$ respectively in the target).
Next, we modify ![]() $\widetilde {F}_{\theta, \mathrm {module}}^{\mathrm {Comm}}$ to get
$\widetilde {F}_{\theta, \mathrm {module}}^{\mathrm {Comm}}$ to get ![]() $F_{\theta, \mathrm {module}}^{\mathrm {Comm}}$ in a similar way as we did for
$F_{\theta, \mathrm {module}}^{\mathrm {Comm}}$ in a similar way as we did for ![]() $\widetilde {F}_\theta ^\mathrm {Comm}$ (2.5.3). The objects in
$\widetilde {F}_\theta ^\mathrm {Comm}$ (2.5.3). The objects in ![]() $N(\mathrm {Fin}_*)_{\langle 1\rangle /}{\bigcirc{\kern-6pt \star}}\Delta ^1$ can be divided into unmarked ones and marked ones, depending on whether its projection to
$N(\mathrm {Fin}_*)_{\langle 1\rangle /}{\bigcirc{\kern-6pt \star}}\Delta ^1$ can be divided into unmarked ones and marked ones, depending on whether its projection to ![]() $N(\mathrm {Fin}_*)_{\langle 1\rangle /}$ is null or not null. If an object
$N(\mathrm {Fin}_*)_{\langle 1\rangle /}$ is null or not null. If an object ![]() $\alpha : \langle 1\rangle \rightarrow \langle n\rangle$ in
$\alpha : \langle 1\rangle \rightarrow \langle n\rangle$ in ![]() $N(\mathrm {Fin}_*)_{\langle 1\rangle /}$ is not null, then we say
$N(\mathrm {Fin}_*)_{\langle 1\rangle /}$ is not null, then we say ![]() $\alpha (1)$ is the marking or marked element in
$\alpha (1)$ is the marking or marked element in ![]() $\langle n\rangle$. For any object
$\langle n\rangle$. For any object ![]() $x$ of in
$x$ of in ![]() $I_{N(\mathrm {Fin}_*)_{\langle 1\rangle/}{\bigcirc{\kern-6pt \star}}\Delta ^1}\underset {I_+^\mathrm {Comm}}{\times } \mathcal {T}_+^\mathrm {Comm}$ over an object of the form
$I_{N(\mathrm {Fin}_*)_{\langle 1\rangle/}{\bigcirc{\kern-6pt \star}}\Delta ^1}\underset {I_+^\mathrm {Comm}}{\times } \mathcal {T}_+^\mathrm {Comm}$ over an object of the form

in ![]() $I_{N(\mathrm {Fin}_*)_{\langle 1\rangle /}{\bigcirc{\kern-6pt \star}}\Delta ^1}$, the projection of
$I_{N(\mathrm {Fin}_*)_{\langle 1\rangle /}{\bigcirc{\kern-6pt \star}}\Delta ^1}$, the projection of ![]() $\widetilde {F}_{\theta, \mathrm {module}}^{\mathrm {Comm}}(x)$ to
$\widetilde {F}_{\theta, \mathrm {module}}^{\mathrm {Comm}}(x)$ to ![]() $N(\mathrm {Fin}_*)$ is, by definition, a subset of one of the above
$N(\mathrm {Fin}_*)$ is, by definition, a subset of one of the above ![]() $\langle n_i\rangle, 0\leq i\leq \mu -1$ and
$\langle n_i\rangle, 0\leq i\leq \mu -1$ and ![]() $\langle m_j\rangle,0\leq j\leq k-\mu$. If it contains the image of
$\langle m_j\rangle,0\leq j\leq k-\mu$. If it contains the image of ![]() $\langle 1\rangle$ in the latter, i.e. the marked element, then we say the image
$\langle 1\rangle$ in the latter, i.e. the marked element, then we say the image ![]() $\widetilde {F}_{\theta, \mathrm {module}}^{\mathrm {Comm}}(x)$ is marked; otherwise we say it is unmarked.
$\widetilde {F}_{\theta, \mathrm {module}}^{\mathrm {Comm}}(x)$ is marked; otherwise we say it is unmarked.
Now for any object ![]() $x$ in
$x$ in ![]() $I_{N(\mathrm {Fin}_*)_{\langle 1\rangle /}{\bigcirc{\kern-6pt \star}} \Delta ^1}\underset {I_+^\mathrm {Comm}}{\times } \mathcal {T}_+^\mathrm {Comm}$, if
$I_{N(\mathrm {Fin}_*)_{\langle 1\rangle /}{\bigcirc{\kern-6pt \star}} \Delta ^1}\underset {I_+^\mathrm {Comm}}{\times } \mathcal {T}_+^\mathrm {Comm}$, if ![]() $\widetilde {F}_{\theta, \mathrm {module}}^{\mathrm {Comm}}(x)$ is unmarked in the above sense, we define
$\widetilde {F}_{\theta, \mathrm {module}}^{\mathrm {Comm}}(x)$ is unmarked in the above sense, we define ![]() $F_{\theta, \mathrm {module}}^{\mathrm {Comm}}(x)$ to be the corresponding element of
$F_{\theta, \mathrm {module}}^{\mathrm {Comm}}(x)$ to be the corresponding element of ![]() $\widetilde {F}_{\theta, \mathrm {module}}^{\mathrm {Comm}}(x)$ in
$\widetilde {F}_{\theta, \mathrm {module}}^{\mathrm {Comm}}(x)$ in ![]() $I_{\widetilde {\pi }_{\dagger} }\underset {\Delta ^1}{\times }\{1\}$ under the identification
$I_{\widetilde {\pi }_{\dagger} }\underset {\Delta ^1}{\times }\{1\}$ under the identification
 \[ I_{\widetilde{\pi}_{\dagger}}\underset{\Delta^1}{\times}\{1\}\simeq N(\mathrm{Fin}_{*})\times \bigg(\Delta^{\{P,C\}}\coprod_{\Delta^{\{P\}}}\Delta^{\{P,D\}}\bigg) \simeq N(\mathrm{Fin}_{*})\times \bigg(\Delta^{\{W,M\}}\coprod_{\Delta^{\{W\}}}\Delta^{\{W,N\}}\bigg), \]
\[ I_{\widetilde{\pi}_{\dagger}}\underset{\Delta^1}{\times}\{1\}\simeq N(\mathrm{Fin}_{*})\times \bigg(\Delta^{\{P,C\}}\coprod_{\Delta^{\{P\}}}\Delta^{\{P,D\}}\bigg) \simeq N(\mathrm{Fin}_{*})\times \bigg(\Delta^{\{W,M\}}\coprod_{\Delta^{\{W\}}}\Delta^{\{W,N\}}\bigg), \]
where in the latter identification, we send ![]() $P\mapsto W, M\mapsto C, N\mapsto D$. If
$P\mapsto W, M\mapsto C, N\mapsto D$. If ![]() $\widetilde {F}_{\theta, \mathrm {module}}^{\mathrm {Comm}}(x)$ is marked, then we define
$\widetilde {F}_{\theta, \mathrm {module}}^{\mathrm {Comm}}(x)$ is marked, then we define ![]() $F_{\theta, \mathrm {module}}^{\mathrm {Comm}}(x)$ to be the corresponding element in
$F_{\theta, \mathrm {module}}^{\mathrm {Comm}}(x)$ to be the corresponding element in
 \[ I_{\widetilde{\pi}_{\dagger}}\underset{\Delta^1}{\times}\{0\}\simeq N(\mathrm{Fin}_{*,{\dagger}})\times \bigg(\Delta^{\{W,M\}}\coprod_{\Delta^{\{W\}}}\Delta^{\{W,N\}}\bigg), \]
\[ I_{\widetilde{\pi}_{\dagger}}\underset{\Delta^1}{\times}\{0\}\simeq N(\mathrm{Fin}_{*,{\dagger}})\times \bigg(\Delta^{\{W,M\}}\coprod_{\Delta^{\{W\}}}\Delta^{\{W,N\}}\bigg), \]
that makes the marking in ![]() $\langle n_x\rangle$ to be
$\langle n_x\rangle$ to be ![]() ${\dagger}$. It is easy to see that these extend to a well-defined functor
${\dagger}$. It is easy to see that these extend to a well-defined functor ![]() $F_{\theta, \mathrm {module}}^{\mathrm {Comm}}$ (2.5.11).
$F_{\theta, \mathrm {module}}^{\mathrm {Comm}}$ (2.5.11).
The right Kan extension of the composition ![]() $MWN\circ F_{\theta, \mathrm {module}}^{\mathrm {Comm}}$ (2.5.10) along
$MWN\circ F_{\theta, \mathrm {module}}^{\mathrm {Comm}}$ (2.5.10) along
gives a functor between coCartesian fibrations
over ![]() $I^\mathrm {Comm}$.
$I^\mathrm {Comm}$.
Proposition 2.24 Assume we are given a commutative diagram (2.5.9) which exhibits ![]() $M^{\bullet,{\dagger} }$,
$M^{\bullet,{\dagger} }$, ![]() $W^{\bullet,{\dagger} }$ and
$W^{\bullet,{\dagger} }$ and ![]() $N^{\bullet,{\dagger} }$ as modules over the commutative algebra objects
$N^{\bullet,{\dagger} }$ as modules over the commutative algebra objects ![]() $C^\bullet$,
$C^\bullet$, ![]() $P^\bullet$ and
$P^\bullet$ and ![]() $D^\bullet$ in
$D^\bullet$ in ![]() $\mathbf {Corr}(\mathcal {C}^\times )$, respectively. Assume that the correspondence
$\mathbf {Corr}(\mathcal {C}^\times )$, respectively. Assume that the correspondence ![]() $D^\bullet \leftarrow P^\bullet \rightarrow C^\bullet$ determines a right-lax algebra homomorphism from the commutative algebra
$D^\bullet \leftarrow P^\bullet \rightarrow C^\bullet$ determines a right-lax algebra homomorphism from the commutative algebra ![]() $C^\bullet$ to
$C^\bullet$ to ![]() $D^\bullet$ in the sense of Theorem 2.13. Then the correspondence (2.5.9) of the pairs naturally determines a right-lax morphism from the pair
$D^\bullet$ in the sense of Theorem 2.13. Then the correspondence (2.5.9) of the pairs naturally determines a right-lax morphism from the pair ![]() $(C^\bullet, M^{\bullet,{\dagger} })$ to
$(C^\bullet, M^{\bullet,{\dagger} })$ to ![]() $(D^\bullet, N^{\bullet,{\dagger} })$ if the diagram
$(D^\bullet, N^{\bullet,{\dagger} })$ if the diagram

is Cartesian for every ![]() $\langle n\rangle _{\dagger}$ in
$\langle n\rangle _{\dagger}$ in ![]() $\mathrm {Fin}_{*,{\dagger} }$. If, in addition, the correspondence
$\mathrm {Fin}_{*,{\dagger} }$. If, in addition, the correspondence ![]() $D^\bullet \leftarrow P^\bullet \rightarrow C^\bullet$ determines an algebra homomorphism and the diagram
$D^\bullet \leftarrow P^\bullet \rightarrow C^\bullet$ determines an algebra homomorphism and the diagram

is Cartesian for the active morphism ![]() $f: \langle 1\rangle _{\dagger} \rightarrow \langle 0\rangle _{\dagger}$ in
$f: \langle 1\rangle _{\dagger} \rightarrow \langle 0\rangle _{\dagger}$ in ![]() $N(\mathrm {Fin}_{*,{\dagger} })$, i.e.
$N(\mathrm {Fin}_{*,{\dagger} })$, i.e. ![]() $f^{-1}(*)=*$, then the same correspondence naturally determines a morphism between the pairs.
$f^{-1}(*)=*$, then the same correspondence naturally determines a morphism between the pairs.
Proof. The proof is almost the same as the proof of Theorem 2.13, in which we only need to check the Cartesian property of the (commutative version of the) diagrams (2.4.13), (2.4.14), and (2.4.16) in the marked case. These are exactly the conditions listed in the proposition.
Proposition 2.24 immediately implies the following.
Corollary 2.25 Assume we are given a commutative algebra object ![]() $C$ in
$C$ in ![]() $\mathbf {Corr}(\mathcal {C}^\times )$, determined by a
$\mathbf {Corr}(\mathcal {C}^\times )$, determined by a ![]() $\mathrm {Fin}_*$-object
$\mathrm {Fin}_*$-object ![]() $C^\bullet$ in
$C^\bullet$ in ![]() $\mathcal {C}$, and a correspondence of
$\mathcal {C}$, and a correspondence of ![]() $\mathrm {Fin}_{*,{\dagger} }$-objects
$\mathrm {Fin}_{*,{\dagger} }$-objects

in ![]() $\mathcal {C}$ as modules over
$\mathcal {C}$ as modules over ![]() $C$ in
$C$ in ![]() $\mathbf {Corr}(\mathcal {C}^\times )$. Then the correspondence naturally determines a right-lax
$\mathbf {Corr}(\mathcal {C}^\times )$. Then the correspondence naturally determines a right-lax ![]() $C$-module morphism from
$C$-module morphism from ![]() $M^{\bullet,{\dagger} }$ to
$M^{\bullet,{\dagger} }$ to ![]() $N^{\bullet,{\dagger} }$ if the diagram
$N^{\bullet,{\dagger} }$ if the diagram

is Cartesian for every ![]() $\langle n\rangle _{\dagger}$ in
$\langle n\rangle _{\dagger}$ in ![]() $\mathrm {Fin}_{*,{\dagger} }$. If, in addition, the diagram
$\mathrm {Fin}_{*,{\dagger} }$. If, in addition, the diagram

is Cartesian for the active ![]() $f: \langle 1\rangle _{\dagger} \rightarrow \langle 0\rangle _{\dagger}$ in
$f: \langle 1\rangle _{\dagger} \rightarrow \langle 0\rangle _{\dagger}$ in ![]() $\mathrm {Fin}_{*,{\dagger} }$, then the same correspondence naturally determines a
$\mathrm {Fin}_{*,{\dagger} }$, then the same correspondence naturally determines a ![]() $C$-module morphism.
$C$-module morphism.
Remark 2.26 As one would expect, the composition of two (right-lax) morphisms between pairs given by two correspondences

is homotopic to the one given by the correspondence

Let ![]() $\mathrm {Fun}_{\mathsf {inert}}(I_{\pi _{\dagger} }, \mathcal {C})$ (respectively,
$\mathrm {Fun}_{\mathsf {inert}}(I_{\pi _{\dagger} }, \mathcal {C})$ (respectively, ![]() $\mathrm {Fun}_{\mathsf {active}}(I_{\pi _{\dagger} },\mathcal {C})$) be the 1-full subcategory of
$\mathrm {Fun}_{\mathsf {active}}(I_{\pi _{\dagger} },\mathcal {C})$) be the 1-full subcategory of ![]() $\mathrm {Fun}(I_{\pi _{\dagger} },\mathcal {C})$ consisting of objects satisfying the condition in Theorem 2.23 and whose morphisms from
$\mathrm {Fun}(I_{\pi _{\dagger} },\mathcal {C})$ consisting of objects satisfying the condition in Theorem 2.23 and whose morphisms from ![]() $W^{\bullet,{\dagger} }\rightarrow P^{\bullet }\circ \pi _{\dagger}$ to
$W^{\bullet,{\dagger} }\rightarrow P^{\bullet }\circ \pi _{\dagger}$ to ![]() $N^{\bullet,{\dagger} }\rightarrow D^{\bullet }\circ \pi _{\dagger}$ (respectively,
$N^{\bullet,{\dagger} }\rightarrow D^{\bullet }\circ \pi _{\dagger}$ (respectively, ![]() $W^{\bullet,{\dagger} }\rightarrow P^{\bullet }\circ \pi _{\dagger}$ to
$W^{\bullet,{\dagger} }\rightarrow P^{\bullet }\circ \pi _{\dagger}$ to ![]() $M^{\bullet,{\dagger} }\rightarrow C^{\bullet }\circ \pi _{\dagger}$) satisfy that the diagrams (2.5.12) (respectively, (2.5.13)) are Cartesian for every
$M^{\bullet,{\dagger} }\rightarrow C^{\bullet }\circ \pi _{\dagger}$) satisfy that the diagrams (2.5.12) (respectively, (2.5.13)) are Cartesian for every ![]() $\langle n\rangle _{\dagger} \in \mathrm {Fin}_{*,{\dagger} }$. One can show with the same argument as in Proposition 2.16 for the following.
$\langle n\rangle _{\dagger} \in \mathrm {Fin}_{*,{\dagger} }$. One can show with the same argument as in Proposition 2.16 for the following.
Proposition 2.27 There are natural functors
 \begin{align*} &\mathrm{Fun}_{\mathsf{inert}}(I_{\pi_{\dagger}}, \mathcal{C})\rightarrow \mathcal{M}\mathrm{od}^{N(\mathrm{Fin}_*)}(\mathrm{Corr}(\mathcal{C}^\times)),\\ &\mathrm{Fun}_{\mathsf{active}}(I_{\pi_{\dagger}},\mathcal{C})^{\rm op}\rightarrow \mathcal{M}\mathrm{od}^{N(\mathrm{Fin}_*)}(\mathrm{Corr}(\mathcal{C}^\times)). \end{align*}
\begin{align*} &\mathrm{Fun}_{\mathsf{inert}}(I_{\pi_{\dagger}}, \mathcal{C})\rightarrow \mathcal{M}\mathrm{od}^{N(\mathrm{Fin}_*)}(\mathrm{Corr}(\mathcal{C}^\times)),\\ &\mathrm{Fun}_{\mathsf{active}}(I_{\pi_{\dagger}},\mathcal{C})^{\rm op}\rightarrow \mathcal{M}\mathrm{od}^{N(\mathrm{Fin}_*)}(\mathrm{Corr}(\mathcal{C}^\times)). \end{align*}
Proposition 2.28 Let ![]() $K,L$ be two
$K,L$ be two ![]() $\infty$-categories. Assume
$\infty$-categories. Assume ![]() $F: K\times L^{\rm op}\rightarrow \mathrm {Fun}(I_{\pi _{\dagger} }, \mathcal {C})$ is a functor satisfying:
$F: K\times L^{\rm op}\rightarrow \mathrm {Fun}(I_{\pi _{\dagger} }, \mathcal {C})$ is a functor satisfying:
(i) for any
 $\ell \in L$ (respectively,
$\ell \in L$ (respectively,  $k\in K$),
$k\in K$),  $F|_{K\times \{\ell \}}$ (respectively,
$F|_{K\times \{\ell \}}$ (respectively,  $F|_{\{k\}\times L^{\rm op}}$) factors through the 1-full subcategory
$F|_{\{k\}\times L^{\rm op}}$) factors through the 1-full subcategory  $\mathrm {Fun}_{\mathsf {inert}}(I_{\pi _{\dagger} }, \mathcal {C})$ (respectively,
$\mathrm {Fun}_{\mathsf {inert}}(I_{\pi _{\dagger} }, \mathcal {C})$ (respectively,  $\mathrm {Fun}_{\mathsf {active}}(I_{\pi _{\dagger} }, \mathcal {C})$);
$\mathrm {Fun}_{\mathsf {active}}(I_{\pi _{\dagger} }, \mathcal {C})$);(ii) the induced functor
 $ev_{\langle 1\rangle }\circ F: K\times L^{\rm op}\rightarrow \mathcal {C}$ (respectively,
$ev_{\langle 1\rangle }\circ F: K\times L^{\rm op}\rightarrow \mathcal {C}$ (respectively,  $ev_{\langle 0\rangle _{\dagger} }\circ F$) satisfies that for any square
$ev_{\langle 0\rangle _{\dagger} }\circ F$) satisfies that for any square  $\alpha : [1]\times [1]^{\rm op}\rightarrow K\times L^{\rm op}$ determined by a functor
$\alpha : [1]\times [1]^{\rm op}\rightarrow K\times L^{\rm op}$ determined by a functor  $\alpha \in \mathrm {Fun}([1],K)\times \mathrm {Fun}([1]^{\rm op},L^{\rm op})$, the diagram
$\alpha \in \mathrm {Fun}([1],K)\times \mathrm {Fun}([1]^{\rm op},L^{\rm op})$, the diagram  $ev_{\langle 1\rangle }\circ F\circ \alpha : [1]\times [1]^{\rm op}\rightarrow \mathcal {C}$ (respectively,
$ev_{\langle 1\rangle }\circ F\circ \alpha : [1]\times [1]^{\rm op}\rightarrow \mathcal {C}$ (respectively,  $ev_{\langle 0\rangle _{\dagger} }\circ F\circ \alpha$) is a Cartesian square;
$ev_{\langle 0\rangle _{\dagger} }\circ F\circ \alpha$) is a Cartesian square;
then ![]() $F$ naturally determines a functor
$F$ naturally determines a functor ![]() $F_{\mathcal {M}\mathrm {od}}: K\times L\rightarrow \mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathrm {Corr}(\mathcal {C}^\times ))$.
$F_{\mathcal {M}\mathrm {od}}: K\times L\rightarrow \mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathrm {Corr}(\mathcal {C}^\times ))$.
3. The functor  $\mathrm {ShvSp}$ out of the category of correspondences
$\mathrm {ShvSp}$ out of the category of correspondences
In this section, we will define the functor
 \begin{align*} \mathrm{ShvSp}:\
&\mathrm{Corr}(\mathrm{S}_{\mathrm{LCH}})\rightarrow
\mathcal{P}\mathrm{r}_{\mathrm{st}}^{\mathrm{L}}\\
& X\mapsto \mathrm{Shv}(X;\mathrm{Sp})
\end{align*}
\begin{align*} \mathrm{ShvSp}:\
&\mathrm{Corr}(\mathrm{S}_{\mathrm{LCH}})\rightarrow
\mathcal{P}\mathrm{r}_{\mathrm{st}}^{\mathrm{L}}\\
& X\mapsto \mathrm{Shv}(X;\mathrm{Sp})
\end{align*}
from Theorem 1.5 and give a proof of the theorem. Moreover, we will show that ![]() $\mathrm {ShvSp}$ is canonically symmetric monoidal. These follow from a direct application of the approach in [Reference Gaitsgory and RozenblyumGR17] to define the functor of taking ind-coherent sheaves out of the category of correspondences of schemes, and the application is based on the foundations of
$\mathrm {ShvSp}$ is canonically symmetric monoidal. These follow from a direct application of the approach in [Reference Gaitsgory and RozenblyumGR17] to define the functor of taking ind-coherent sheaves out of the category of correspondences of schemes, and the application is based on the foundations of ![]() $\infty$-topoi (see [Reference LurieLur09]) and stable
$\infty$-topoi (see [Reference LurieLur09]) and stable ![]() $\infty$-categories (see [Reference LurieLur17]). We have provided the references for each step explicitly.
$\infty$-categories (see [Reference LurieLur17]). We have provided the references for each step explicitly.
3.1 The functor  $\mathrm {ShvSp}_!: \mathrm {S}_{\mathrm {LCH}}\rightarrow \mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$
$\mathrm {ShvSp}_!: \mathrm {S}_{\mathrm {LCH}}\rightarrow \mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$
We recall some basic definitions and useful facts about the ![]() $\infty$-category of sheaves on a topological space with values in an (stable)
$\infty$-category of sheaves on a topological space with values in an (stable) ![]() $\infty$-category from [Reference LurieLur09] and [Reference LurieLur17]. For any topological space
$\infty$-category from [Reference LurieLur09] and [Reference LurieLur17]. For any topological space ![]() $X$, let
$X$, let ![]() $\mathcal {U}(X)$ be the poset of open subsets in
$\mathcal {U}(X)$ be the poset of open subsets in ![]() $X$. Let
$X$. Let ![]() $\mathcal {C}$ be any
$\mathcal {C}$ be any ![]() $\infty$-category that admits small limits. Let
$\infty$-category that admits small limits. Let ![]() $\mathcal {P}(X;\mathcal {C})=\mathrm {Fun}(N(\mathcal {U}(X))^{\rm op}, \mathcal {C})$ be the
$\mathcal {P}(X;\mathcal {C})=\mathrm {Fun}(N(\mathcal {U}(X))^{\rm op}, \mathcal {C})$ be the ![]() $\infty$-category of
$\infty$-category of ![]() $\mathcal {C}$-valued presheaves on
$\mathcal {C}$-valued presheaves on ![]() $X$. For any subset
$X$. For any subset ![]() $S\subset X$, let
$S\subset X$, let ![]() $\mathcal {F}(S)=\varinjlim _{S\subset U}\mathcal {F}(U)$.
$\mathcal {F}(S)=\varinjlim _{S\subset U}\mathcal {F}(U)$.
Definition 3.1 A ![]() $\mathcal {C}$-valued sheaf on
$\mathcal {C}$-valued sheaf on ![]() $X$ is an object
$X$ is an object ![]() $\mathcal {F}$ in
$\mathcal {F}$ in ![]() $\mathcal {P}(X;\mathcal {C})$ satisfying that if
$\mathcal {P}(X;\mathcal {C})$ satisfying that if ![]() $\{U_i\subset U\}_{i\in I}$ is an open cover of
$\{U_i\subset U\}_{i\in I}$ is an open cover of ![]() $U$, then the natural morphism
$U$, then the natural morphism
 \[ \mathcal{F}(U)\rightarrow \varprojlim_{\emptyset\neq J\subset I}\mathcal{F} \bigg(\bigcap_{j\in J}U_j\bigg) \]
\[ \mathcal{F}(U)\rightarrow \varprojlim_{\emptyset\neq J\subset I}\mathcal{F} \bigg(\bigcap_{j\in J}U_j\bigg) \]
is an isomorphism in ![]() $\mathcal {C}$. We denote the full subcategory of
$\mathcal {C}$. We denote the full subcategory of ![]() $\mathcal {P}(X;\mathcal {C})$ consisting of
$\mathcal {P}(X;\mathcal {C})$ consisting of ![]() $\mathcal {C}$-valued sheaves by
$\mathcal {C}$-valued sheaves by ![]() $\mathrm {Shv}(X;\mathcal {C})$.
$\mathrm {Shv}(X;\mathcal {C})$.
Any continuous map ![]() $f: X\rightarrow Y$ induces a functor
$f: X\rightarrow Y$ induces a functor ![]() $f^{-1}: N(\mathcal {U}(Y))^{\rm op}\rightarrow N(\mathcal {U}(X))^{\rm op}$, which gives rise to the functor
$f^{-1}: N(\mathcal {U}(Y))^{\rm op}\rightarrow N(\mathcal {U}(X))^{\rm op}$, which gives rise to the functor ![]() $f_*: \mathcal {P}(X;\mathcal {C})\rightarrow \mathcal {P}(Y;\mathcal {C})$. It is straightforward from the definition that
$f_*: \mathcal {P}(X;\mathcal {C})\rightarrow \mathcal {P}(Y;\mathcal {C})$. It is straightforward from the definition that ![]() $f_*$ sends a sheaf to a sheaf. Thus, we have a well-defined functor
$f_*$ sends a sheaf to a sheaf. Thus, we have a well-defined functor ![]() $\mathrm {Shv}\mathcal {C}: \mathrm {S}_{\mathrm {Top}}\rightarrow 1\text {-}\mathcal {C}\mathrm {at}$ from the ordinary 1-category of topological spaces to the
$\mathrm {Shv}\mathcal {C}: \mathrm {S}_{\mathrm {Top}}\rightarrow 1\text {-}\mathcal {C}\mathrm {at}$ from the ordinary 1-category of topological spaces to the ![]() $\infty$-category of
$\infty$-category of ![]() $\infty$-categories.
$\infty$-categories.
Now following notation in [Reference LurieLur09], let ![]() $\mathrm {Shv}(X)$ (respectively,
$\mathrm {Shv}(X)$ (respectively, ![]() $\mathcal {P}(X)$) denote the
$\mathcal {P}(X)$) denote the ![]() $\infty$-category of
$\infty$-category of ![]() $\mathcal {S}\mathrm {pc}$-valued sheaves (respectively, presheaves) on
$\mathcal {S}\mathrm {pc}$-valued sheaves (respectively, presheaves) on ![]() $X$. The functor
$X$. The functor ![]() $f_*$ admits a left adjoint
$f_*$ admits a left adjoint ![]() $f^*$.
$f^*$.
In particular, we see that ![]() $f^*$ preserves small colimits and finite limits, and
$f^*$ preserves small colimits and finite limits, and ![]() $f_*$ preserves small limits and finite colimits, using the adjunction and:
$f_*$ preserves small limits and finite colimits, using the adjunction and:
–
 $f^*$ on presheaves preserves finite limits and
$f^*$ on presheaves preserves finite limits and  $f_*$ on presheaves preserves small colimits;
$f_*$ on presheaves preserves small colimits;– sheafification commutes with finite limits and small colimits [Reference LurieLur09, Proposition 6.2.2.7];
– the inclusion
 $\mathrm {Shv}(X)\hookrightarrow \mathcal {P}(X)$ preserves small limits and finite colimits.
$\mathrm {Shv}(X)\hookrightarrow \mathcal {P}(X)$ preserves small limits and finite colimits.
When ![]() $f$ is an open embedding,
$f$ is an open embedding, ![]() $f^*$ preserves small limits, so it admits a left adjoint denoted by
$f^*$ preserves small limits, so it admits a left adjoint denoted by ![]() $f_!$. When
$f_!$. When ![]() $f$ is proper,
$f$ is proper, ![]() $f_*$ preserves small colimits. In the following, we will focus on
$f_*$ preserves small colimits. In the following, we will focus on ![]() $\mathrm {Shv}(X;\mathrm {Sp})$, the stable
$\mathrm {Shv}(X;\mathrm {Sp})$, the stable ![]() $\infty$-category of sheaves of spectra on
$\infty$-category of sheaves of spectra on ![]() $X$, which can be obtained by taking stabilization of
$X$, which can be obtained by taking stabilization of ![]() $\mathrm {Shv}(X)$ (cf. [Reference LurieLur17, § 1.4.2]).
$\mathrm {Shv}(X)$ (cf. [Reference LurieLur17, § 1.4.2]).
Let ![]() $\mathrm {S}_{\mathrm {LCH}}$ be the ordinary 1-category of locally compact Hausdorff spaces. There are two ways to define
$\mathrm {S}_{\mathrm {LCH}}$ be the ordinary 1-category of locally compact Hausdorff spaces. There are two ways to define ![]() $f_!: \mathrm {Shv}(X;\mathrm {Sp})\rightarrow \mathrm {Shv}(Y;\mathrm {Sp})$ for any morphism
$f_!: \mathrm {Shv}(X;\mathrm {Sp})\rightarrow \mathrm {Shv}(Y;\mathrm {Sp})$ for any morphism ![]() $f:X\rightarrow Y$ in
$f:X\rightarrow Y$ in ![]() $\mathrm {S}_{\mathrm {LCH}}$. One is to use the fact that
$\mathrm {S}_{\mathrm {LCH}}$. One is to use the fact that ![]() $f_!$ is the left (respectively, right) adjoint of
$f_!$ is the left (respectively, right) adjoint of ![]() $f^*$ for
$f^*$ for ![]() $f$ an open embedding (respectively, proper), and decompose every morphism into the composition of an open embedding followed by a proper map. The construction needs to invoke the machinery developed in [Reference Gaitsgory and RozenblyumGR17]. The other way is to use the self-duality of
$f$ an open embedding (respectively, proper), and decompose every morphism into the composition of an open embedding followed by a proper map. The construction needs to invoke the machinery developed in [Reference Gaitsgory and RozenblyumGR17]. The other way is to use the self-duality of ![]() $\mathrm {Shv}(X;\mathrm {Sp})$ as a dualizable object in
$\mathrm {Shv}(X;\mathrm {Sp})$ as a dualizable object in ![]() $\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$ proved in [Reference LurieLur18, Propositions 21.1.6.12 and 21.1.7.1, Appendix D.7.3] and
$\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$ proved in [Reference LurieLur18, Propositions 21.1.6.12 and 21.1.7.1, Appendix D.7.3] and ![]() $f_!$ is just the dual of
$f_!$ is just the dual of ![]() $f^*$, and we also get
$f^*$, and we also get ![]() $f^!$ directly as the right adjoint of
$f^!$ directly as the right adjoint of ![]() $f_!$. We will adopt the latter definition, for it gives us a convenient way to follow the steps in [Reference Gaitsgory and RozenblyumGR17] to define the functor
$f_!$. We will adopt the latter definition, for it gives us a convenient way to follow the steps in [Reference Gaitsgory and RozenblyumGR17] to define the functor ![]() $\mathrm {ShvSp}$ of taking sheaves of spectra out of the category of correspondences in
$\mathrm {ShvSp}$ of taking sheaves of spectra out of the category of correspondences in ![]() $\mathrm {S}_{\mathrm {LCH}}$. We will denote the resulting functor as
$\mathrm {S}_{\mathrm {LCH}}$. We will denote the resulting functor as
 \begin{align} \mathrm{ShvSp}_!:\ &
\mathrm{S}_{\mathrm{LCH}}\rightarrow
\mathbf{Pr}_{\mathrm{st}}^{\mathrm{L}}\\
& X\mapsto \mathrm{Shv}(X; \mathrm{Sp}),\nonumber\\ & (f:
X\rightarrow Y)\mapsto (f_!:
\mathrm{Shv}(X;\mathrm{Sp})\rightarrow
\mathrm{Shv}(Y;\mathrm{Sp})). \nonumber
\end{align}
\begin{align} \mathrm{ShvSp}_!:\ &
\mathrm{S}_{\mathrm{LCH}}\rightarrow
\mathbf{Pr}_{\mathrm{st}}^{\mathrm{L}}\\
& X\mapsto \mathrm{Shv}(X; \mathrm{Sp}),\nonumber\\ & (f:
X\rightarrow Y)\mapsto (f_!:
\mathrm{Shv}(X;\mathrm{Sp})\rightarrow
\mathrm{Shv}(Y;\mathrm{Sp})). \nonumber
\end{align}
We state a lemma which will be used soon.
Lemma 3.2 Let

be any Cartesian diagram of locally compact Hausdorff spaces.
(i) If
 $q'$ is an open embedding (then so is
$q'$ is an open embedding (then so is  $q$), then the natural transformation
arising from applying adjunctions to the natural isomorphism
$q$), then the natural transformation
arising from applying adjunctions to the natural isomorphism \[ p_!q^*\rightarrow (q')^*(p')_!: \mathrm{Shv}(X;\mathrm{Sp})\rightarrow \mathrm{Shv}(Y;\mathrm{Sp}) \]
is an isomorphism of functors.
\[ p_!q^*\rightarrow (q')^*(p')_!: \mathrm{Shv}(X;\mathrm{Sp})\rightarrow \mathrm{Shv}(Y;\mathrm{Sp}) \]
is an isomorphism of functors. \[ (q')_!p_!\simeq p'_!q_! \]
\[ (q')_!p_!\simeq p'_!q_! \]
(ii) If
 $q'$ is proper (then so is
$q'$ is proper (then so is  $q$), then the natural transformation
arising from applying adjunctions to the natural isomorphism
$q$), then the natural transformation
arising from applying adjunctions to the natural isomorphism \[ (q')^*(p')_!\rightarrow p_!q^*: \mathrm{Shv}(X;\mathrm{Sp})\rightarrow \mathrm{Shv}(Y;\mathrm{Sp}) \]
is an isomorphism of functors.
\[ (q')^*(p')_!\rightarrow p_!q^*: \mathrm{Shv}(X;\mathrm{Sp})\rightarrow \mathrm{Shv}(Y;\mathrm{Sp}) \]
is an isomorphism of functors. \begin{align*} (q')_*p_!\simeq p'_!q_* \end{align*}
\begin{align*} (q')_*p_!\simeq p'_!q_* \end{align*}
Proof. (i) Since ![]() $q'$ and
$q'$ and ![]() $q$ are open embeddings, this is clear from the definition of the functors.
$q$ are open embeddings, this is clear from the definition of the functors.
(ii) Applying the self-duality on the sheaf categories, it suffices to prove that the natural transformation
is an isomorphism of functors. Since ![]() $q'_!\simeq q'_*, q_!\simeq q_*$, this is just the stable version of the nonabelian proper base change theorem [Reference LurieLur09, Corollary 7.3.1.18].
$q'_!\simeq q'_*, q_!\simeq q_*$, this is just the stable version of the nonabelian proper base change theorem [Reference LurieLur09, Corollary 7.3.1.18].
3.2 Definition of  $\mathrm {ShvSp}_{\mathsf {all},\mathsf {all}}^{\mathsf {prop}}: \mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {all},\mathsf {all}}^{\mathsf {prop}}\rightarrow (\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{2\text {-}{\rm op}}$
$\mathrm {ShvSp}_{\mathsf {all},\mathsf {all}}^{\mathsf {prop}}: \mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {all},\mathsf {all}}^{\mathsf {prop}}\rightarrow (\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{2\text {-}{\rm op}}$
We follow the steps in [Reference Gaitsgory and RozenblyumGR17, Chapter 5, § 2] to define the canonical functor
where the superscript ![]() $2\text {-}{\rm op}$ means reversing the 2-morphisms. Moreover, we will show that
$2\text {-}{\rm op}$ means reversing the 2-morphisms. Moreover, we will show that ![]() $\mathrm {ShvSp}_{\mathsf {all},\mathsf {all}}^{\mathsf {prop}}$ is canonically symmetric monoidal.
$\mathrm {ShvSp}_{\mathsf {all},\mathsf {all}}^{\mathsf {prop}}$ is canonically symmetric monoidal.
First, let
which satisfy the conditions in [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 5.1.1–5.1.2]. We start from the functor (3.1.1)
First, by Lemma 3.2(i), ![]() $\mathrm {ShvSp}_!$ satisfies the left Beck–Chevalley condition (cf. [Reference Gaitsgory and RozenblyumGR17, Chapter 7, Definition 3.1.2]) with respect to open maps, therefore by [Reference Gaitsgory and RozenblyumGR17, Theorem 3.2.2], it uniquely determines a functor
$\mathrm {ShvSp}_!$ satisfies the left Beck–Chevalley condition (cf. [Reference Gaitsgory and RozenblyumGR17, Chapter 7, Definition 3.1.2]) with respect to open maps, therefore by [Reference Gaitsgory and RozenblyumGR17, Theorem 3.2.2], it uniquely determines a functor
Now by [Reference Gaitsgory and RozenblyumGR17, Theorem 4.1.3], the restriction of ![]() $\mathrm {ShvSp}_{\mathsf {all},\mathsf {open}}^{\mathsf {open}}$ to
$\mathrm {ShvSp}_{\mathsf {all},\mathsf {open}}^{\mathsf {open}}$ to
loses no information.
Next, we apply [Reference Gaitsgory and RozenblyumGR17, Chapter 7, Theorem 5.2.4] to give the canonical extension of ![]() $\mathrm {ShvSp}_{\mathsf {all},\mathsf {open}}^{\mathsf {isom}}$ to
$\mathrm {ShvSp}_{\mathsf {all},\mathsf {open}}^{\mathsf {isom}}$ to
Note that the restriction ![]() $\mathrm {ShvSp}_{\mathsf {all},\mathsf {open}}^{\mathsf {isom}}|_{(\mathrm {S}_{\mathrm {LCH}})_{vert}}$ satisfies the left Beck–Chevalley condition for
$\mathrm {ShvSp}_{\mathsf {all},\mathsf {open}}^{\mathsf {isom}}|_{(\mathrm {S}_{\mathrm {LCH}})_{vert}}$ satisfies the left Beck–Chevalley condition for ![]() $adm=\mathsf {prop}\subset vert=\mathsf {all}$ if we view the target as
$adm=\mathsf {prop}\subset vert=\mathsf {all}$ if we view the target as ![]() $(\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{2\text {-}{\rm op}}$. This follows from Lemma 3.2(ii). Hence, to apply the theorem, we only need to check the conditions in [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 5.1.4 and 5.2.2].
$(\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{2\text {-}{\rm op}}$. This follows from Lemma 3.2(ii). Hence, to apply the theorem, we only need to check the conditions in [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 5.1.4 and 5.2.2].
The condition in [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 5.1.4] in our setting says the following. For any ![]() $\alpha : X\rightarrow Y$ in
$\alpha : X\rightarrow Y$ in ![]() $horiz=\mathsf {all}$, consider the ordinary 1-category
$horiz=\mathsf {all}$, consider the ordinary 1-category ![]() $\mathrm {Factor}(\alpha )$ of factorizations of
$\mathrm {Factor}(\alpha )$ of factorizations of ![]() $\alpha$ into an open embedding followed by a proper map.
$\alpha$ into an open embedding followed by a proper map.
(i) An object in
 $\mathrm {Factor}(\alpha )$ is a sequence of maps
such that
$\mathrm {Factor}(\alpha )$ is a sequence of maps
such that \[ X\overset{f}{\rightarrow }Z\overset{g}{\rightarrow }Y \]
\[ X\overset{f}{\rightarrow }Z\overset{g}{\rightarrow }Y \]
 $g\circ f=\alpha$,
$g\circ f=\alpha$,  $f\in \mathsf {open}$ and
$f\in \mathsf {open}$ and  $g\in \mathsf {prop}$.
$g\in \mathsf {prop}$.(ii) A morphism from
to \begin{align*} X\overset{f}{\rightarrow }Z\overset{g}{\rightarrow }Y \end{align*}
is a morphism
\begin{align*} X\overset{f}{\rightarrow }Z\overset{g}{\rightarrow }Y \end{align*}
is a morphism \[ X\overset{f'}{\rightarrow }Z'\overset{g'}{\rightarrow }Y \]
\[ X\overset{f'}{\rightarrow }Z'\overset{g'}{\rightarrow }Y \]
 $\beta : Z\rightarrow Z'$ that makes the following diagram commute.
$\beta : Z\rightarrow Z'$ that makes the following diagram commute.

We need to show that ![]() $\mathrm {Factor}(\alpha )$ is contractible. Recall that a 1-category is contractible if the geometric realization of its nerve is contractible.
$\mathrm {Factor}(\alpha )$ is contractible. Recall that a 1-category is contractible if the geometric realization of its nerve is contractible.
Lemma 3.3 For any ![]() $\alpha$,
$\alpha$, ![]() $\mathrm {Factor}(\alpha )$ is contractible.
$\mathrm {Factor}(\alpha )$ is contractible.
Proof. The proof follows the same line as the proof of [Reference Gaitsgory and RozenblyumGR17, Chapter 5, Proposition 2.1.6], but significantly simpler than the scheme setting there. First, one shows that ![]() $\mathrm {Factor}(\alpha )$ is nonempty. Choose a compactification
$\mathrm {Factor}(\alpha )$ is nonempty. Choose a compactification ![]() $\overline {X}$ of
$\overline {X}$ of ![]() $X$, say the one-point compactification, and let
$X$, say the one-point compactification, and let
Then the natural embedding ![]() $X\hookrightarrow Z$ is open and the projection from
$X\hookrightarrow Z$ is open and the projection from ![]() $Z$ to
$Z$ to ![]() $Y$ is proper, and their composition is
$Y$ is proper, and their composition is ![]() $\alpha$.
$\alpha$.
Let ![]() $\mathrm {Factor}(\alpha )_{\mathrm {dense}}$ be the full subcategory of
$\mathrm {Factor}(\alpha )_{\mathrm {dense}}$ be the full subcategory of ![]() $\mathrm {Factor}(\alpha )$ whose objects are factorizations
$\mathrm {Factor}(\alpha )$ whose objects are factorizations ![]() $X\overset {f}{\rightarrow } Z\overset {g}{\rightarrow } Y$ with
$X\overset {f}{\rightarrow } Z\overset {g}{\rightarrow } Y$ with ![]() $\overline {f(X)}=Z$. Because of the transitivity of taking closures for any sequence of maps
$\overline {f(X)}=Z$. Because of the transitivity of taking closures for any sequence of maps ![]() $A\overset {u}{\rightarrow } B\overset {v }{\rightarrow } C$, i.e.
$A\overset {u}{\rightarrow } B\overset {v }{\rightarrow } C$, i.e. ![]() $\overline {v\circ u(A)}=\overline {v(\overline {u(A)})}$. The inclusion
$\overline {v\circ u(A)}=\overline {v(\overline {u(A)})}$. The inclusion ![]() $\mathrm {Factor}(\alpha )_{\mathrm {dense}}\hookrightarrow \mathrm {Factor}(\alpha )$ admits a right adjoint, so one just need to show that
$\mathrm {Factor}(\alpha )_{\mathrm {dense}}\hookrightarrow \mathrm {Factor}(\alpha )$ admits a right adjoint, so one just need to show that ![]() $\mathrm {Factor}(\alpha )_{\mathrm {dense}}$ is contractible.
$\mathrm {Factor}(\alpha )_{\mathrm {dense}}$ is contractible.
Lastly, one shows that ![]() $\mathrm {Factor}(\alpha )_{\mathrm {dense}}$ admits products, so then we have a functor
$\mathrm {Factor}(\alpha )_{\mathrm {dense}}$ admits products, so then we have a functor ![]() $\mathrm {Factor}(\alpha )_{\mathrm {dense}}\times \mathrm {Factor}(\alpha )_{\mathrm {dense}}\rightarrow \mathrm {Factor}(\alpha )_{\mathrm {dense}}$ that admits a left adjoint, and this would imply
$\mathrm {Factor}(\alpha )_{\mathrm {dense}}\times \mathrm {Factor}(\alpha )_{\mathrm {dense}}\rightarrow \mathrm {Factor}(\alpha )_{\mathrm {dense}}$ that admits a left adjoint, and this would imply ![]() $\mathrm {Factor}(\alpha )_{\mathrm {dense}}$ is contractible. For any two factorizations in
$\mathrm {Factor}(\alpha )_{\mathrm {dense}}$ is contractible. For any two factorizations in ![]() $\mathrm {Factor}(\alpha )_{\mathrm {dense}}$,
$\mathrm {Factor}(\alpha )_{\mathrm {dense}}$,
let ![]() $W$ be the closure of the image of
$W$ be the closure of the image of ![]() $X$ in
$X$ in ![]() $Z\underset {Y}{\times }Z'$ under
$Z\underset {Y}{\times }Z'$ under ![]() $(f,f')$. One can easily check that the factorization
$(f,f')$. One can easily check that the factorization ![]() $X\rightarrow W\rightarrow Y$ serves as the product of the two in (3.2.1).
$X\rightarrow W\rightarrow Y$ serves as the product of the two in (3.2.1).
Next, we check the condition of [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 5.2.2], which says that for any Cartesian diagram

with ![]() $j_X,j_Y\in \mathsf {open}$ and
$j_X,j_Y\in \mathsf {open}$ and ![]() $p_1,p_2\in \mathsf {prop}$, the natural transformation
$p_1,p_2\in \mathsf {prop}$, the natural transformation
arising from applying adjunctions to the isomorphism from base change
needs to be an isomorphism. Since ![]() $j_X^!\simeq j_X^*, j_Y^!\simeq j_Y^*$, the condition obviously holds.
$j_X^!\simeq j_X^*, j_Y^!\simeq j_Y^*$, the condition obviously holds.
Having finished the check of the conditions for applying [Reference Gaitsgory and RozenblyumGR17, Chapter 7, Theorem 5.2.4], we now obtain the canonical functor
3.3 Symmetric monoidal structure on  $\mathrm {ShvSp}_{\mathsf {all},\mathsf {all}}^{\mathsf {prop}}$
$\mathrm {ShvSp}_{\mathsf {all},\mathsf {all}}^{\mathsf {prop}}$
3.3.1 The symmetric monoidal structure on  $\mathrm {ShvSp}_!: \mathrm {S}_{\mathrm {LCH}}\rightarrow \mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$
$\mathrm {ShvSp}_!: \mathrm {S}_{\mathrm {LCH}}\rightarrow \mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$
Let
 \begin{align*} \mathrm{Shv}^*:\ &\mathrm{S}_{\mathrm{LCH}}^{\rm op}\rightarrow \mathcal{P}\mathrm{r}^{\mathrm{L}}\\ &X\mapsto \mathrm{Shv}(X)\\ &(f:X\rightarrow Y)\mapsto (f^*: \mathrm{Shv}(Y)\rightarrow \mathrm{Shv}(X)) \end{align*}
\begin{align*} \mathrm{Shv}^*:\ &\mathrm{S}_{\mathrm{LCH}}^{\rm op}\rightarrow \mathcal{P}\mathrm{r}^{\mathrm{L}}\\ &X\mapsto \mathrm{Shv}(X)\\ &(f:X\rightarrow Y)\mapsto (f^*: \mathrm{Shv}(Y)\rightarrow \mathrm{Shv}(X)) \end{align*}
be the functor associated to ![]() $*$-pullback. It is proven in [Reference LurieLur09] that the functor
$*$-pullback. It is proven in [Reference LurieLur09] that the functor ![]() $\mathrm {Shv}^*$ is symmetric monoidal (see [Reference LurieLur09, Proposition 7.3.1.11]). Since
$\mathrm {Shv}^*$ is symmetric monoidal (see [Reference LurieLur09, Proposition 7.3.1.11]). Since ![]() $\mathrm {ShvSp}_!$ is the composition of
$\mathrm {ShvSp}_!$ is the composition of ![]() $\mathrm {Shv}^*$ with the functor
$\mathrm {Shv}^*$ with the functor ![]() $\mathcal {P}\mathrm {r}^{\mathrm {L}}\rightarrow \mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$ of taking stabilizations, followed by the functor of taking the dual category on the full subcategory of dualizable objects in
$\mathcal {P}\mathrm {r}^{\mathrm {L}}\rightarrow \mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$ of taking stabilizations, followed by the functor of taking the dual category on the full subcategory of dualizable objects in ![]() $\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$, we have
$\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$, we have
is symmetric monoidal as well.
Now applying the same argument as in [Reference Gaitsgory and RozenblyumGR17, Chapter 9, Proposition 3.1.2 and 3.1.5], we get that the symmetric monoidal structure on ![]() $\mathrm {ShvSp}_!$ uniquely extends to a symmetric monoidal structure on
$\mathrm {ShvSp}_!$ uniquely extends to a symmetric monoidal structure on ![]() $\mathrm {ShvSp}_{\mathsf {all},\mathsf {open}}^{\mathsf {isom}}$, which further uniquely extends to a symmetric monoidal structure on
$\mathrm {ShvSp}_{\mathsf {all},\mathsf {open}}^{\mathsf {isom}}$, which further uniquely extends to a symmetric monoidal structure on ![]() $\mathrm {ShvSp}_{\mathsf {all}, \mathsf {all}}^{\mathsf {prop}}$. In summary, we have proved the following.
$\mathrm {ShvSp}_{\mathsf {all}, \mathsf {all}}^{\mathsf {prop}}$. In summary, we have proved the following.
Theorem 3.4 The functor
is equipped with a canonical symmetric monoidal structure.
Proof of Theorem 1.5 We define ![]() $\mathrm {ShvSp}^*_!$ as the restriction of
$\mathrm {ShvSp}^*_!$ as the restriction of ![]() $\mathrm {ShvSp}_{\mathsf {all}, \mathsf {all}}^{\mathsf {prop}}$ to
$\mathrm {ShvSp}_{\mathsf {all}, \mathsf {all}}^{\mathsf {prop}}$ to ![]() $adm=\mathsf {isom}$.
$adm=\mathsf {isom}$.
By an entire similar process, one gets a canonical symmetric monoidal functor ![]() $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {all},\mathsf {all}}^{\mathsf {prop}}\rightarrow \mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}}$, by taking
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {all},\mathsf {all}}^{\mathsf {prop}}\rightarrow \mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}}$, by taking ![]() $!$-pullback and
$!$-pullback and ![]() $*$-pushforward. Alternatively, by taking
$*$-pushforward. Alternatively, by taking ![]() $1\text {-}{\rm op}$ on both sides of (3.3.1), using that
$1\text {-}{\rm op}$ on both sides of (3.3.1), using that ![]() $(\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{1\& 2\text {-}\mathrm {op}}\simeq \mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}}$ and
$(\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{1\& 2\text {-}\mathrm {op}}\simeq \mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}}$ and ![]() $(\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {all},\mathsf {all}}^{\mathsf {prop}})^{1\text {-}{\rm op}}\simeq \mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {all},\mathsf {all}}^{\mathsf {prop}}$, we get
$(\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {all},\mathsf {all}}^{\mathsf {prop}})^{1\text {-}{\rm op}}\simeq \mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {all},\mathsf {all}}^{\mathsf {prop}}$, we get ![]() $\mathrm {ShvSp}^!_*$ as well. Restricting
$\mathrm {ShvSp}^!_*$ as well. Restricting ![]() $adm=\mathsf {isom}$, this is exactly Corollary 1.6.
$adm=\mathsf {isom}$, this is exactly Corollary 1.6.
3.3.2 Symmetric monoidal structure on taking local system categories out of correspondences
Now we restrict our vertical arrows to locally trivial fibrations, denoted by ![]() $\mathsf {fib}$, and consider the functor induced from
$\mathsf {fib}$, and consider the functor induced from ![]() $\mathrm {ShvSp}_{\mathsf {all},\mathsf {all}}^{\mathsf {prop}}$ by restricting the image to the full subcategory of locally constant sheaves:
$\mathrm {ShvSp}_{\mathsf {all},\mathsf {all}}^{\mathsf {prop}}$ by restricting the image to the full subcategory of locally constant sheaves:
 \begin{align} (\mathrm{Loc}')_{!}^*:\ &\mathrm{Corr}(\mathrm{S}_{\mathrm{LCH}})_{\mathsf{fib},\mathsf{all}}\rightarrow \mathcal{P}\mathrm{r}_{\mathrm{st}}^{\mathrm{L}}\\ &X\mapsto \mathrm{Loc}'(X;\mathrm{Sp}). \nonumber \end{align}
\begin{align} (\mathrm{Loc}')_{!}^*:\ &\mathrm{Corr}(\mathrm{S}_{\mathrm{LCH}})_{\mathsf{fib},\mathsf{all}}\rightarrow \mathcal{P}\mathrm{r}_{\mathrm{st}}^{\mathrm{L}}\\ &X\mapsto \mathrm{Loc}'(X;\mathrm{Sp}). \nonumber \end{align}
It is a symmetric monoidal functor, since ![]() $\boxtimes : \mathrm {Loc}'(X;\mathrm {Sp})\otimes \mathrm {Loc}'(Y;\mathrm {Sp})\to \mathrm {Loc}'(X\times Y;\mathrm {Sp})$ is an equivalence.
$\boxtimes : \mathrm {Loc}'(X;\mathrm {Sp})\otimes \mathrm {Loc}'(Y;\mathrm {Sp})\to \mathrm {Loc}'(X\times Y;\mathrm {Sp})$ is an equivalence.
On the other hand, we have the symmetric monoidal functor ![]() $\mathrm {Loc}_*^!$ (1.7.3) already defined in § 1.7.
$\mathrm {Loc}_*^!$ (1.7.3) already defined in § 1.7.
Later, we also use the natural symmetric monoidal functor ![]() $\mathrm {Loc}\mathrm {Sp}_!: \mathcal {S}\mathrm {pc}\rightarrow \mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$ that takes a CW-complex
$\mathrm {Loc}\mathrm {Sp}_!: \mathcal {S}\mathrm {pc}\rightarrow \mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$ that takes a CW-complex ![]() $X$ to
$X$ to ![]() $\mathrm {Loc}(X;\mathrm {Sp})$ and
$\mathrm {Loc}(X;\mathrm {Sp})$ and ![]() $f: X\rightarrow Y$ to
$f: X\rightarrow Y$ to ![]() $f_!$ (with right adjoint
$f_!$ (with right adjoint ![]() $f^!$). Here again, we regard a local system on
$f^!$). Here again, we regard a local system on ![]() $X$ as a locally constant cosheaf, through the equivalence
$X$ as a locally constant cosheaf, through the equivalence ![]() $\mathrm {Loc}(X, \mathrm {Sp})\simeq \mathrm {Fun}(X; \mathrm {Sp})$ (cf. Remark 1.7). When
$\mathrm {Loc}(X, \mathrm {Sp})\simeq \mathrm {Fun}(X; \mathrm {Sp})$ (cf. Remark 1.7). When ![]() $X\in \mathrm {S}_{\mathrm {LCH}}$, the constant cosheaf with fiber
$X\in \mathrm {S}_{\mathrm {LCH}}$, the constant cosheaf with fiber ![]() $\mathbf {S}$ is exactly the dualizing sheaf
$\mathbf {S}$ is exactly the dualizing sheaf ![]() $\varpi _X:=f^!\mathbf {S}_{pt}$, for the map
$\varpi _X:=f^!\mathbf {S}_{pt}$, for the map ![]() $f: X\rightarrow \mathit {pt}$. Then
$f: X\rightarrow \mathit {pt}$. Then ![]() $f_!\varpi _X$ is the homology of
$f_!\varpi _X$ is the homology of ![]() $X$ (with coefficient in
$X$ (with coefficient in ![]() $\mathbf {S}$), i.e.
$\mathbf {S}$), i.e. ![]() $\Sigma _+^\infty X$, while
$\Sigma _+^\infty X$, while ![]() $f_*\varpi _X$ is the Borel–Moore homology of
$f_*\varpi _X$ is the Borel–Moore homology of ![]() $X$, i.e.
$X$, i.e. ![]() $\Sigma ^\infty X^c$, where
$\Sigma ^\infty X^c$, where ![]() $X^c$ is the one-point compactification of
$X^c$ is the one-point compactification of ![]() $X$ as a pointed space. For example, if
$X$ as a pointed space. For example, if ![]() $X=V$ is a finite-dimensional vector space, then
$X=V$ is a finite-dimensional vector space, then ![]() $f_!$ and
$f_!$ and ![]() $f^!$ are inverse equivalences between
$f^!$ are inverse equivalences between ![]() $\mathrm {Loc}(V;\mathrm {Sp})$ and
$\mathrm {Loc}(V;\mathrm {Sp})$ and ![]() $\mathrm {Loc}(pt;\mathrm {Sp})\simeq \mathrm {Sp}$, so
$\mathrm {Loc}(pt;\mathrm {Sp})\simeq \mathrm {Sp}$, so ![]() $f_!\varpi _V\simeq f_!f^!\mathbf {S}\simeq \mathbf {S}$. On the other hand, let
$f_!\varpi _V\simeq f_!f^!\mathbf {S}\simeq \mathbf {S}$. On the other hand, let ![]() $j: V\hookrightarrow V^c$ and
$j: V\hookrightarrow V^c$ and ![]() $i: \{x\}\hookrightarrow V^c$ be the open and closed inclusions, where
$i: \{x\}\hookrightarrow V^c$ be the open and closed inclusions, where ![]() $\{x\}$ is the complement of
$\{x\}$ is the complement of ![]() $V$ in
$V$ in ![]() $V^c$. Let
$V^c$. Let ![]() $\overline {f}: V^c\to pt$ be the obvious map. Using the standard fiber sequence
$\overline {f}: V^c\to pt$ be the obvious map. Using the standard fiber sequence
in ![]() $\mathrm {Shv}(V^c;\mathrm {Sp})$ and applying
$\mathrm {Shv}(V^c;\mathrm {Sp})$ and applying ![]() $\overline {f}_*\simeq \overline {f}_!$, we get a fiber sequence in
$\overline {f}_*\simeq \overline {f}_!$, we get a fiber sequence in ![]() $\mathrm {Sp}$,
$\mathrm {Sp}$,
which says that ![]() $f_*\varpi _V$ is exactly calculating the reduced homology of
$f_*\varpi _V$ is exactly calculating the reduced homology of ![]() $V^c$, i.e.
$V^c$, i.e. ![]() $\Sigma ^\infty V^c$.
$\Sigma ^\infty V^c$.
4. Quantization of the Hamiltonian  $\coprod _nBO(n)$-action and the
$\coprod _nBO(n)$-action and the  $J$-homomorphism
$J$-homomorphism
In this section, we use sheaves of spectra to quantize the Hamiltonian ![]() $\coprod _nBO(n)$-action and its ‘module’ generated by the stabilization of
$\coprod _nBO(n)$-action and its ‘module’ generated by the stabilization of ![]() $L_0=\mathrm {graph}(d(-\frac {1}{2}|\mathbf {q}|^2))$ in
$L_0=\mathrm {graph}(d(-\frac {1}{2}|\mathbf {q}|^2))$ in ![]() $T^*\mathbf {R}^M$. This is an application of the various results that we have developed in § 2 concerning (commutative) algebra/module objects in
$T^*\mathbf {R}^M$. This is an application of the various results that we have developed in § 2 concerning (commutative) algebra/module objects in ![]() $\mathrm {Corr}(\mathcal {C})$ and the morphisms between them, for the case
$\mathrm {Corr}(\mathcal {C})$ and the morphisms between them, for the case ![]() $\mathcal {C}=\mathrm {S}_{\mathrm {LCH}}$. We first list the relevant algebra/module objects in
$\mathcal {C}=\mathrm {S}_{\mathrm {LCH}}$. We first list the relevant algebra/module objects in ![]() $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$ and morphisms between them, and then we give a model of the
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$ and morphisms between them, and then we give a model of the ![]() $J$-homomorphism based on correspondences, and the quantization result will be an immediate consequence of these.
$J$-homomorphism based on correspondences, and the quantization result will be an immediate consequence of these.
4.1 The relevant algebra/module objects in  $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$
Recall that we let ![]() $A$ denote a quadratic form on
$A$ denote a quadratic form on ![]() $\mathbf {R}^N$ whose symmetric matrix relative to the standard basis of
$\mathbf {R}^N$ whose symmetric matrix relative to the standard basis of ![]() $\mathbf {R}^N$ is idempotent. We equally view
$\mathbf {R}^N$ is idempotent. We equally view ![]() $A$ as the eigenspace of eigenvalue
$A$ as the eigenspace of eigenvalue ![]() $1$ of its symmetric matrix and in this way
$1$ of its symmetric matrix and in this way ![]() $A$ is also regarded as an element of
$A$ is also regarded as an element of ![]() $\coprod _nBO(n)$.
$\coprod _nBO(n)$.
We first define the ![]() $\mathrm {Fin}_*$-object
$\mathrm {Fin}_*$-object ![]() $G_N^\bullet$ in
$G_N^\bullet$ in ![]() $\mathrm {S}_{\mathrm {LCH}}$. Let
$\mathrm {S}_{\mathrm {LCH}}$. Let
Here ![]() $G_N^{\langle 0\rangle }=\mathit {pt}$. For any
$G_N^{\langle 0\rangle }=\mathit {pt}$. For any ![]() $f: \langle n \rangle \rightarrow \langle m\rangle$ in
$f: \langle n \rangle \rightarrow \langle m\rangle$ in ![]() $N(\mathrm {Fin}_*)$, define the associated morphism
$N(\mathrm {Fin}_*)$, define the associated morphism
 \begin{align*} G_N^{\langle n\rangle}&\rightarrow G_N^{\langle m\rangle}\\ (A_i)_{i\in\langle n\rangle^\circ}&\mapsto \bigg(\bigoplus_{i\in f^{-1}(j)}A_i\bigg)_{j\in\langle m\rangle^\circ}. \end{align*}
\begin{align*} G_N^{\langle n\rangle}&\rightarrow G_N^{\langle m\rangle}\\ (A_i)_{i\in\langle n\rangle^\circ}&\mapsto \bigg(\bigoplus_{i\in f^{-1}(j)}A_i\bigg)_{j\in\langle m\rangle^\circ}. \end{align*}
Here we take the convention that if ![]() $f^{-1}(j)=\emptyset$, then
$f^{-1}(j)=\emptyset$, then ![]() $\bigoplus _{i\in f^{-1}(j)}A_i=0$. It is easy to see that
$\bigoplus _{i\in f^{-1}(j)}A_i=0$. It is easy to see that ![]() $G_N^\bullet$ is a well-defined
$G_N^\bullet$ is a well-defined ![]() $\mathrm {Fin}_*$-object in
$\mathrm {Fin}_*$-object in ![]() $\mathrm {S}_{\mathrm {LCH}}$.
$\mathrm {S}_{\mathrm {LCH}}$.
Lemma 4.1 The ![]() $\mathrm {Fin}_*$-object
$\mathrm {Fin}_*$-object ![]() $G_N^{\bullet }$ represents a commutative algebra object in
$G_N^{\bullet }$ represents a commutative algebra object in ![]() $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$ in the sense of Theorem 2.8.
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$ in the sense of Theorem 2.8.
Proof. By Theorem 2.8, we just need to check that every diagram (2.3.7) is Cartesian and the vertical maps are in ![]() $\mathsf {fib}$, for any active morphism
$\mathsf {fib}$, for any active morphism ![]() $f: \langle m\rangle \rightarrow \langle n\rangle$, but this is straightforward.
$f: \langle m\rangle \rightarrow \langle n\rangle$, but this is straightforward.
Remark 4.2 We can also use a simplicial object ![]() $G_N^\bullet$ to represent the associative algebra structure on
$G_N^\bullet$ to represent the associative algebra structure on ![]() $G_N$ in
$G_N$ in ![]() $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$. The
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$. The ![]() $\mathrm {Fin}_*$-object (respectively, simplicial object)
$\mathrm {Fin}_*$-object (respectively, simplicial object) ![]() $G_N^{\bullet }$ is not a commutative Segal object (respectively, Segal object) in
$G_N^{\bullet }$ is not a commutative Segal object (respectively, Segal object) in ![]() $\mathrm {S}_{\mathrm {LCH}}$, but it represents a commutative (respectively, associative) algebra object in
$\mathrm {S}_{\mathrm {LCH}}$, but it represents a commutative (respectively, associative) algebra object in ![]() $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$.
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$.
Similarly to ![]() $G_N^\bullet$, let
$G_N^\bullet$, let
 \begin{align*}
\widehat{G}_{N,M}^{\langle
n\rangle}&=\bigg\{\!\bigg(A_1,\ldots, A_n;
\mathbf{q},\mathbf{q}+\sum_{i=1}^n \partial_{\mathbf{p}}
A_i(\mathbf{p}_i); t=\sum_{i=1}^n A_i(\mathbf{p}_i)\bigg):
\mathbf{p}_i\in \mathbf{R}^M\bigg\}\\ &\subset G_N^{\langle
n\rangle}\times \mathbf{R}^M\times \mathbf{R}^M\times
\mathbf{R}. \end{align*}
\begin{align*}
\widehat{G}_{N,M}^{\langle
n\rangle}&=\bigg\{\!\bigg(A_1,\ldots, A_n;
\mathbf{q},\mathbf{q}+\sum_{i=1}^n \partial_{\mathbf{p}}
A_i(\mathbf{p}_i); t=\sum_{i=1}^n A_i(\mathbf{p}_i)\bigg):
\mathbf{p}_i\in \mathbf{R}^M\bigg\}\\ &\subset G_N^{\langle
n\rangle}\times \mathbf{R}^M\times \mathbf{R}^M\times
\mathbf{R}. \end{align*}
Equivalently, we can denote an element in ![]() $\widehat {G}_{N,M}^{\langle n\rangle }$ by
$\widehat {G}_{N,M}^{\langle n\rangle }$ by
 \[ (A_1,\ldots,A_n;\mathbf{p}_1,\ldots,\mathbf{p}_n;\mathbf{q},t),\quad \mathbf{p}_i\in A_i, \quad t=\sum_{i=1}^n|\mathbf{p}_i|^2. \]
\[ (A_1,\ldots,A_n;\mathbf{p}_1,\ldots,\mathbf{p}_n;\mathbf{q},t),\quad \mathbf{p}_i\in A_i, \quad t=\sum_{i=1}^n|\mathbf{p}_i|^2. \]
Note that ![]() $\varinjlim _{N,M}\widehat {G}_{N,M}^{\langle 1\rangle }$ is the front projection of the (stabilized) conic Lagrangian lifting of the graph of the Hamiltonian action of
$\varinjlim _{N,M}\widehat {G}_{N,M}^{\langle 1\rangle }$ is the front projection of the (stabilized) conic Lagrangian lifting of the graph of the Hamiltonian action of ![]() $\coprod _nBO(n)$ (see the beginning of § 5.1 for the definition of conic Lagrangian liftings). For any
$\coprod _nBO(n)$ (see the beginning of § 5.1 for the definition of conic Lagrangian liftings). For any ![]() $f: \langle n\rangle \rightarrow \langle m\rangle$ in
$f: \langle n\rangle \rightarrow \langle m\rangle$ in ![]() $N(\mathrm {Fin}_*)$, we define
$N(\mathrm {Fin}_*)$, we define
 \begin{align*} &\widehat{G}_{N,M}^{\langle n\rangle}\rightarrow \widehat{G}_{N,M}^{\langle m\rangle}\\ &\bigg((A_i)_{i\in \langle n\rangle^\circ}; \mathbf{q},\mathbf{q}+\sum_{i=1}^n \partial_{\mathbf{p}} A_i(\mathbf{p}_i); t=\sum_{i=1}^n A_i(\mathbf{p}_i)\bigg)\\ &\quad \mapsto \bigg(\bigg(\bigoplus_{i\in f^{-1}(j)}A_i\bigg)_{j\in \langle m\rangle^\circ}; \mathbf{q},\mathbf{q}+\sum_{i\in f^{-1}(\langle m\rangle^\circ)}\partial_{\mathbf{p}}A_i(\mathbf{p}_i); t=\sum_{i\in f^{-1}(\langle m\rangle^\circ)}A_i(\mathbf{p}_i)\bigg). \end{align*}
\begin{align*} &\widehat{G}_{N,M}^{\langle n\rangle}\rightarrow \widehat{G}_{N,M}^{\langle m\rangle}\\ &\bigg((A_i)_{i\in \langle n\rangle^\circ}; \mathbf{q},\mathbf{q}+\sum_{i=1}^n \partial_{\mathbf{p}} A_i(\mathbf{p}_i); t=\sum_{i=1}^n A_i(\mathbf{p}_i)\bigg)\\ &\quad \mapsto \bigg(\bigg(\bigoplus_{i\in f^{-1}(j)}A_i\bigg)_{j\in \langle m\rangle^\circ}; \mathbf{q},\mathbf{q}+\sum_{i\in f^{-1}(\langle m\rangle^\circ)}\partial_{\mathbf{p}}A_i(\mathbf{p}_i); t=\sum_{i\in f^{-1}(\langle m\rangle^\circ)}A_i(\mathbf{p}_i)\bigg). \end{align*}
It is direct to check that ![]() $\widehat {G}_{N,M}^\bullet$ defines a
$\widehat {G}_{N,M}^\bullet$ defines a ![]() $\mathrm {Fin}_*$-object in
$\mathrm {Fin}_*$-object in ![]() $\mathrm {S}_{\mathrm {LCH}}$.
$\mathrm {S}_{\mathrm {LCH}}$.
Lemma 4.3 The ![]() $\mathrm {Fin}_*$-object
$\mathrm {Fin}_*$-object ![]() $\widehat {G}_{N,M}^\bullet$ defines a commutative algebra object in
$\widehat {G}_{N,M}^\bullet$ defines a commutative algebra object in ![]() $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$ in the sense of Theorem 2.8, and the natural projection
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$ in the sense of Theorem 2.8, and the natural projection ![]() $\widehat {G}_{N,M}^\bullet \rightarrow G_N^\bullet$, viewed as a correspondence from
$\widehat {G}_{N,M}^\bullet \rightarrow G_N^\bullet$, viewed as a correspondence from ![]() $\widehat {G}_{N,M}^\bullet$ to
$\widehat {G}_{N,M}^\bullet$ to ![]() $G_N^\bullet$ defines an algebra homomorphism from
$G_N^\bullet$ defines an algebra homomorphism from ![]() $\widehat {G}_{N,M}^\bullet$ to
$\widehat {G}_{N,M}^\bullet$ to ![]() $G_N^\bullet$ in
$G_N^\bullet$ in ![]() $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$ in the sense of Theorem 2.13.
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$ in the sense of Theorem 2.13.
Proof. For the first part of the lemma, we just need to check that for any active map ![]() $f: \langle m\rangle \rightarrow \langle n\rangle$ the diagram
$f: \langle m\rangle \rightarrow \langle n\rangle$ the diagram

is Cartesian in ![]() $\mathrm {S}_{\mathrm {LCH}}$. This is easy to see, as the image of the bottom horizontal map consists of
$\mathrm {S}_{\mathrm {LCH}}$. This is easy to see, as the image of the bottom horizontal map consists of ![]() $(A_i,\mathbf {q}, \mathbf {q}+\partial _\mathbf {p} A_i(\mathbf {p}_i), t=A_i(\mathbf {p}_i))_{1\leq i\leq n}$, where
$(A_i,\mathbf {q}, \mathbf {q}+\partial _\mathbf {p} A_i(\mathbf {p}_i), t=A_i(\mathbf {p}_i))_{1\leq i\leq n}$, where ![]() $A_i, 1\leq i\leq n$ are mutually orthogonal, and the right vertical arrow further decomposes each
$A_i, 1\leq i\leq n$ are mutually orthogonal, and the right vertical arrow further decomposes each ![]() $A_i$ into orthogonal pieces (or makes it 0 if
$A_i$ into orthogonal pieces (or makes it 0 if ![]() $f^{-1}(i)=\emptyset$).
$f^{-1}(i)=\emptyset$).
For the second part of the lemma, we only need to check the diagram

is Cartesian in ![]() $\mathrm {S}_{\mathrm {LCH}}$ for each
$\mathrm {S}_{\mathrm {LCH}}$ for each ![]() $n$. This is also straightforward.
$n$. This is also straightforward.
Let ![]() $VG_{N}^\bullet : N(\mathrm {Fin}_*)\rightarrow \mathrm {S}_{\mathrm {LCH}}$ be the
$VG_{N}^\bullet : N(\mathrm {Fin}_*)\rightarrow \mathrm {S}_{\mathrm {LCH}}$ be the ![]() $\mathrm {Fin}_*$-object that takes
$\mathrm {Fin}_*$-object that takes ![]() $\langle n\rangle$ to the tautological vector bundle on
$\langle n\rangle$ to the tautological vector bundle on ![]() $G_N^{\langle n\rangle }$, and we have an obvious isomorphism
$G_N^{\langle n\rangle }$, and we have an obvious isomorphism
Note that ![]() $\widehat {G}_{N,M}^{\bullet }\cong VG_{N}^\bullet \times (\mathbf {R}^M)^{\mathrm {const},\bullet }$, where
$\widehat {G}_{N,M}^{\bullet }\cong VG_{N}^\bullet \times (\mathbf {R}^M)^{\mathrm {const},\bullet }$, where ![]() $(\mathbf {R}^M)^{\mathrm {const},\bullet }$ is the constant
$(\mathbf {R}^M)^{\mathrm {const},\bullet }$ is the constant ![]() $\mathrm {Fin}_*$-object mentioned in Remark 2.10 that gives a commutative algebra object in
$\mathrm {Fin}_*$-object mentioned in Remark 2.10 that gives a commutative algebra object in ![]() $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})$. Since there is a natural equivalence
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})$. Since there is a natural equivalence
where ![]() $\otimes _c$ represents the symmetric monoidal convolution structure induced after taking
$\otimes _c$ represents the symmetric monoidal convolution structure induced after taking ![]() $\mathrm {Loc}_*^!$, in the following quantization process, we will replace
$\mathrm {Loc}_*^!$, in the following quantization process, we will replace ![]() $\widehat {G}_{N,M}^{\bullet }$ by
$\widehat {G}_{N,M}^{\bullet }$ by ![]() $VG_N^\bullet$ without losing any information.
$VG_N^\bullet$ without losing any information.
Lemma 4.4 The correspondence of ![]() $\mathrm {Fin}_*$-objects
$\mathrm {Fin}_*$-objects ![]() $G_N^\bullet \leftarrow VG_N^\bullet \rightarrow G_N^\bullet$ determines an algebra endomorphism of the commutative algebra object in
$G_N^\bullet \leftarrow VG_N^\bullet \rightarrow G_N^\bullet$ determines an algebra endomorphism of the commutative algebra object in ![]() $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$ corresponding to
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$ corresponding to ![]() $G_N^\bullet$.
$G_N^\bullet$.
Proof. This directly follows from Theorem 2.13.
4.1.1 A module object  $\widehat {Q}_{N, M}^{\bullet,{\dagger} }$ of
$\widehat {Q}_{N, M}^{\bullet,{\dagger} }$ of  $VG_{N}^\bullet$
$VG_{N}^\bullet$
Let ![]() $\widehat {Q}_{N,M}^{\langle n\rangle _{{\dagger} }}$ be the subvariety of
$\widehat {Q}_{N,M}^{\langle n\rangle _{{\dagger} }}$ be the subvariety of ![]() $G^{\langle n\rangle }_{N}\times (G_{N}\times \mathbf {R}^M\times \mathbf {R}^M\times \mathbf {R})$ consisting of points
$G^{\langle n\rangle }_{N}\times (G_{N}\times \mathbf {R}^M\times \mathbf {R}^M\times \mathbf {R})$ consisting of points
 \begin{equation} \bigg(A_1,\ldots, A_n; A, \mathbf{q},\mathbf{q}+\sum_{i=1}^n \partial_{\mathbf{p}} A_i(\mathbf{p}_i);s\bigg),\ s< -\frac{1}{2}|\mathbf{q}|^2+A(\mathbf{q}), A\perp \bigoplus_{i\in \langle n\rangle^\circ}A_i. \end{equation}
\begin{equation} \bigg(A_1,\ldots, A_n; A, \mathbf{q},\mathbf{q}+\sum_{i=1}^n \partial_{\mathbf{p}} A_i(\mathbf{p}_i);s\bigg),\ s< -\frac{1}{2}|\mathbf{q}|^2+A(\mathbf{q}), A\perp \bigoplus_{i\in \langle n\rangle^\circ}A_i. \end{equation}
Here and after, we use the convention that for a simplicial object (respectively, ![]() $\mathrm {Fin}_*$-object)
$\mathrm {Fin}_*$-object) ![]() $C^\bullet$ in
$C^\bullet$ in ![]() $\mathcal {C}$ that represents an associative (respectively, commutative) algebra object in
$\mathcal {C}$ that represents an associative (respectively, commutative) algebra object in ![]() $\mathrm {Corr}(\mathcal {C})$, we regard
$\mathrm {Corr}(\mathcal {C})$, we regard ![]() $C^{[1]}$ (respectively,
$C^{[1]}$ (respectively, ![]() $C^{\langle 1\rangle }$) as the underlying object of the algebra object and denote it by
$C^{\langle 1\rangle }$) as the underlying object of the algebra object and denote it by ![]() $C$. Similar convention applies to module objects. For any
$C$. Similar convention applies to module objects. For any ![]() $f: \langle n\rangle _{\dagger} \rightarrow \langle m\rangle _{\dagger}$ in
$f: \langle n\rangle _{\dagger} \rightarrow \langle m\rangle _{\dagger}$ in ![]() $N(\mathrm {Fin}_{*,{\dagger} })$, we let
$N(\mathrm {Fin}_{*,{\dagger} })$, we let
 \begin{align}
&\widehat{Q}_{N,M}^{\langle n\rangle_{\dagger}}\rightarrow
\widehat{Q}_{N,M}^{\langle m\rangle_{\dagger}}\nonumber\\
&\bigg(A_1,\ldots, A_n; A,
\mathbf{q},\mathbf{q}+\sum_{i=1}^n \partial_{\mathbf{p}}
A_i(\mathbf{p}_i); s\bigg) \nonumber\\
&\quad \!\mapsto\bigg(\bigg(\bigoplus_{i\in
f^{-1}(j)}A_i\bigg)_{j\in \langle m\rangle^\circ};
A+\bigoplus_{i\in f^{-1}({\dagger})\backslash
\{{\dagger}\}}A_i, \mathbf{q}+\sum_{i\in
f^{-1}({\dagger})\backslash
\{{\dagger}\}}\partial_{\mathbf{p}}A_i(\mathbf{p}_i),
\nonumber\\ &\qquad\quad\ \mathbf{q}+\sum_{i\in f^{-1}(\langle
m\rangle^\circ\cup {\dagger})\backslash
{\dagger}}\partial_{\mathbf{p}}A_i(\mathbf{p}_i);
s+\sum_{i\in f^{-1}\langle
{\dagger}\rangle\backslash\{{\dagger}\}}A_i(\mathbf{p}_i)\bigg).
\end{align}
\begin{align}
&\widehat{Q}_{N,M}^{\langle n\rangle_{\dagger}}\rightarrow
\widehat{Q}_{N,M}^{\langle m\rangle_{\dagger}}\nonumber\\
&\bigg(A_1,\ldots, A_n; A,
\mathbf{q},\mathbf{q}+\sum_{i=1}^n \partial_{\mathbf{p}}
A_i(\mathbf{p}_i); s\bigg) \nonumber\\
&\quad \!\mapsto\bigg(\bigg(\bigoplus_{i\in
f^{-1}(j)}A_i\bigg)_{j\in \langle m\rangle^\circ};
A+\bigoplus_{i\in f^{-1}({\dagger})\backslash
\{{\dagger}\}}A_i, \mathbf{q}+\sum_{i\in
f^{-1}({\dagger})\backslash
\{{\dagger}\}}\partial_{\mathbf{p}}A_i(\mathbf{p}_i),
\nonumber\\ &\qquad\quad\ \mathbf{q}+\sum_{i\in f^{-1}(\langle
m\rangle^\circ\cup {\dagger})\backslash
{\dagger}}\partial_{\mathbf{p}}A_i(\mathbf{p}_i);
s+\sum_{i\in f^{-1}\langle
{\dagger}\rangle\backslash\{{\dagger}\}}A_i(\mathbf{p}_i)\bigg).
\end{align}
In the following, for any ![]() $A\in \coprod _nBO(n)$, we use
$A\in \coprod _nBO(n)$, we use ![]() $\mathbf {q}^A$ (respectively,
$\mathbf {q}^A$ (respectively, ![]() $\mathbf {q}^{A^\perp }$) to denote the orthogonal projection of
$\mathbf {q}^{A^\perp }$) to denote the orthogonal projection of ![]() $\mathbf {q}$ onto
$\mathbf {q}$ onto ![]() $A$ (respectively, the orthogonal complement of
$A$ (respectively, the orthogonal complement of ![]() $A$).
$A$).
Lemma 4.5
(a) The map (4.1.2) is well defined, i.e. we have
(4.1.3) \begin{align} s+\sum_{i\in
f^{-1}({\dagger})\backslash\{{\dagger}\}}A_i(\mathbf{p}_i)<
&-\frac{1}{2}\bigg|\mathbf{q}+\sum_{i\in
f^{-1}({\dagger})\backslash
\{{\dagger}\}}\partial_{\mathbf{p}}A_i(\mathbf{p}_i)\bigg|^2+A\bigg(\mathbf{q}+\sum_{i\in
f^{-1}({\dagger})\backslash
\{{\dagger}\}}\partial_{\mathbf{p}}A_i(\mathbf{p}_i)\bigg)\nonumber\\
&+\sum_{i\in f^{-1}({\dagger})\backslash \{{\dagger}\}}A_i
\bigg(\mathbf{q}+\sum_{j\in f^{-1}({\dagger})\backslash
\{{\dagger}\}}\partial_{\mathbf{p}}A_j(\mathbf{p}_i)\bigg).
\end{align}
\begin{align} s+\sum_{i\in
f^{-1}({\dagger})\backslash\{{\dagger}\}}A_i(\mathbf{p}_i)<
&-\frac{1}{2}\bigg|\mathbf{q}+\sum_{i\in
f^{-1}({\dagger})\backslash
\{{\dagger}\}}\partial_{\mathbf{p}}A_i(\mathbf{p}_i)\bigg|^2+A\bigg(\mathbf{q}+\sum_{i\in
f^{-1}({\dagger})\backslash
\{{\dagger}\}}\partial_{\mathbf{p}}A_i(\mathbf{p}_i)\bigg)\nonumber\\
&+\sum_{i\in f^{-1}({\dagger})\backslash \{{\dagger}\}}A_i
\bigg(\mathbf{q}+\sum_{j\in f^{-1}({\dagger})\backslash
\{{\dagger}\}}\partial_{\mathbf{p}}A_j(\mathbf{p}_i)\bigg).
\end{align}
(b) For any active map
 $f: \langle n\rangle _{\dagger} \rightarrow \langle 0\rangle _{\dagger}$ in
$f: \langle n\rangle _{\dagger} \rightarrow \langle 0\rangle _{\dagger}$ in  $N(\mathrm {Fin}_{*,{\dagger} })$, the map
is in
$N(\mathrm {Fin}_{*,{\dagger} })$, the map
is in \[ \widehat{Q}_{N,M}^{\langle n\rangle_{\dagger}}\rightarrow \widehat{Q}_{N,M}^{\langle 0\rangle_{\dagger}} \]
\[ \widehat{Q}_{N,M}^{\langle n\rangle_{\dagger}}\rightarrow \widehat{Q}_{N,M}^{\langle 0\rangle_{\dagger}} \]
 $\mathsf {fib}$.
$\mathsf {fib}$.
Proof. For part (a), we only need to show the case for ![]() $f: \langle n\rangle _{\dagger} \rightarrow \langle 0\rangle _{\dagger}$ an active map in
$f: \langle n\rangle _{\dagger} \rightarrow \langle 0\rangle _{\dagger}$ an active map in ![]() $N(\mathrm {Fin}_{*,{\dagger} })$. We will prove parts (a) and (b) simultaneously. For any fixed
$N(\mathrm {Fin}_{*,{\dagger} })$. We will prove parts (a) and (b) simultaneously. For any fixed ![]() $(\widetilde {A},\widetilde {\mathbf {q}},\widetilde {s})\in G_N\times \mathbf {R}^M\times \mathbf {R}_{\widetilde {s}}$, we are going to solve for
$(\widetilde {A},\widetilde {\mathbf {q}},\widetilde {s})\in G_N\times \mathbf {R}^M\times \mathbf {R}_{\widetilde {s}}$, we are going to solve for ![]() $(A_1,\ldots, A_n,\mathbf {p}_1,\ldots,\mathbf {p}_n; A,\mathbf {q}, s)$ satisfying
$(A_1,\ldots, A_n,\mathbf {p}_1,\ldots,\mathbf {p}_n; A,\mathbf {q}, s)$ satisfying
 \begin{align*} & s+\sum_i A_i(\mathbf{p}_i)=\widetilde{s},\quad A\oplus\bigoplus_iA_i=\widetilde{A},\quad \mathbf{q}+\sum_i2\mathbf{p}_i=\widetilde{\mathbf{q}},\\ & s<-\frac{1}{2}|\mathbf{q}|^2+A(\mathbf{q}). \end{align*}
\begin{align*} & s+\sum_i A_i(\mathbf{p}_i)=\widetilde{s},\quad A\oplus\bigoplus_iA_i=\widetilde{A},\quad \mathbf{q}+\sum_i2\mathbf{p}_i=\widetilde{\mathbf{q}},\\ & s<-\frac{1}{2}|\mathbf{q}|^2+A(\mathbf{q}). \end{align*}
This amounts to the inequality for ![]() $A_i,\mathbf {p}_i,\ i=1,\ldots,n$,
$A_i,\mathbf {p}_i,\ i=1,\ldots,n$,
 \begin{align}
&\widetilde{s}-\sum_iA_i(\mathbf{p}_i)<-\frac{1}{2}
\bigg|\widetilde{\mathbf{q}}-\sum_i
2\mathbf{p}_i\bigg|^2+|\widetilde{\mathbf{q}}^A|^2\nonumber\\
\Leftrightarrow\ &\widetilde{s}+\frac{1}{2}|\widetilde{\mathbf{q}}|^2-\widetilde{A}(\widetilde{\mathbf{q}})<-\sum_i|\widetilde{\mathbf{q}}^{A_i}-\mathbf{p}_i|^2.
\end{align}
\begin{align}
&\widetilde{s}-\sum_iA_i(\mathbf{p}_i)<-\frac{1}{2}
\bigg|\widetilde{\mathbf{q}}-\sum_i
2\mathbf{p}_i\bigg|^2+|\widetilde{\mathbf{q}}^A|^2\nonumber\\
\Leftrightarrow\ &\widetilde{s}+\frac{1}{2}|\widetilde{\mathbf{q}}|^2-\widetilde{A}(\widetilde{\mathbf{q}})<-\sum_i|\widetilde{\mathbf{q}}^{A_i}-\mathbf{p}_i|^2.
\end{align}
Only when
the inequality (4.1.4) has a solution. Thus, part (a) is established. The fiber over ![]() $(\widetilde {A},\widetilde {\mathbf {q}},\widetilde {s})\in \widehat {Q}_{N,M}^{\langle 0\rangle _{\dagger} }$ is the union of (open) disc bundles (or a point if
$(\widetilde {A},\widetilde {\mathbf {q}},\widetilde {s})\in \widehat {Q}_{N,M}^{\langle 0\rangle _{\dagger} }$ is the union of (open) disc bundles (or a point if ![]() $A=\widetilde {A}$) over the partial flag varieties of
$A=\widetilde {A}$) over the partial flag varieties of ![]() $\widetilde {A}$
$\widetilde {A}$
 \[ \bigg\{(A_1,\ldots, A_n,A): A\oplus \bigoplus_{i}A_i=\widetilde{A}\bigg\}, \]
\[ \bigg\{(A_1,\ldots, A_n,A): A\oplus \bigoplus_{i}A_i=\widetilde{A}\bigg\}, \]
so part (b) follows.
Now it is easy to see that ![]() $\widehat {Q}_{N,M}^{\bullet,{\dagger} }$ is a
$\widehat {Q}_{N,M}^{\bullet,{\dagger} }$ is a ![]() $\mathrm {Fin}_{*,{\dagger} }$-object. We have a natural map
$\mathrm {Fin}_{*,{\dagger} }$-object. We have a natural map
 \begin{align*} &\widehat{Q}_{N,M}^{\langle n\rangle_{\dagger}}\rightarrow VG_{N}^{\langle n\rangle}\\ &\bigg(A_1,\ldots, A_n; A, \mathbf{q},\mathbf{q}+\sum_{i=1}^n \partial_{\mathbf{p}} A_i(\mathbf{p}_i);s\bigg) \mapsto \bigg(A_1,\ldots,A_n; \sum_{i=1}^n \partial_{\mathbf{p}} A_i(\mathbf{p}_i); t=\sum_{i=1}^n A_i(\mathbf{p}_i)\bigg), \end{align*}
\begin{align*} &\widehat{Q}_{N,M}^{\langle n\rangle_{\dagger}}\rightarrow VG_{N}^{\langle n\rangle}\\ &\bigg(A_1,\ldots, A_n; A, \mathbf{q},\mathbf{q}+\sum_{i=1}^n \partial_{\mathbf{p}} A_i(\mathbf{p}_i);s\bigg) \mapsto \bigg(A_1,\ldots,A_n; \sum_{i=1}^n \partial_{\mathbf{p}} A_i(\mathbf{p}_i); t=\sum_{i=1}^n A_i(\mathbf{p}_i)\bigg), \end{align*}
for each ![]() $n$, that defines a natural transformation
$n$, that defines a natural transformation ![]() $\widehat {Q}_{N,M}^{\bullet,{\dagger} }\rightarrow VG_{N}^{\bullet }\circ \pi _{\dagger}$.
$\widehat {Q}_{N,M}^{\bullet,{\dagger} }\rightarrow VG_{N}^{\bullet }\circ \pi _{\dagger}$.
Lemma 4.6 The natural transformation ![]() $\widehat {Q}_{N,M}^{\bullet,{\dagger} }\rightarrow VG_{N}^{\bullet }\circ \pi _{\dagger}$ exhibits
$\widehat {Q}_{N,M}^{\bullet,{\dagger} }\rightarrow VG_{N}^{\bullet }\circ \pi _{\dagger}$ exhibits ![]() $\widehat {Q}_{N,M}^{\bullet,{\dagger} }$ as a module of
$\widehat {Q}_{N,M}^{\bullet,{\dagger} }$ as a module of ![]() $VG_{N}^{\bullet }$ in
$VG_{N}^{\bullet }$ in ![]() $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$.
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$.
Proof. By Theorem 2.23, we just need to show that for any active ![]() $f: \langle n\rangle _{\dagger} \rightarrow \langle m\rangle _{\dagger}$, the diagram
$f: \langle n\rangle _{\dagger} \rightarrow \langle m\rangle _{\dagger}$, the diagram

is Cartesian in ![]() $\mathrm {S}_{\mathrm {LCH}}$. Writing things out explicitly, the bottom horizontal map is
$\mathrm {S}_{\mathrm {LCH}}$. Writing things out explicitly, the bottom horizontal map is
 \begin{align*} &(A_1,\ldots, A_m; A, \mathbf{q},\mathbf{q}+\sum_{i=1}^m \partial_{\mathbf{p}} A_i(\mathbf{p}_i); s)\\ &\quad \mapsto((A_k, \partial_\mathbf{p} A_k(\mathbf{p}_k), t_k=A_k(\mathbf{p}_k))_{k\in \langle m\rangle^\circ}, (A, \mathbf{q},\mathbf{q}; s)) \end{align*}
\begin{align*} &(A_1,\ldots, A_m; A, \mathbf{q},\mathbf{q}+\sum_{i=1}^m \partial_{\mathbf{p}} A_i(\mathbf{p}_i); s)\\ &\quad \mapsto((A_k, \partial_\mathbf{p} A_k(\mathbf{p}_k), t_k=A_k(\mathbf{p}_k))_{k\in \langle m\rangle^\circ}, (A, \mathbf{q},\mathbf{q}; s)) \end{align*}
and the right vertical map is
 \begin{align*}
&\bigg(\bigg((A_{k,j_k})_{j_k\in f^{-1}(k)}; \sum_{j_k\in
f^{-1}(k)}\partial_\mathbf{p}
A_{k,j_k}(\mathbf{p}_{k,j_k}), t_k\bigg)_{k\in \langle
m\rangle^\circ}, \\ &\qquad (A_\alpha)_{\alpha\in
f^{-1}({\dagger})\backslash {\dagger}}; A, \mathbf{q},
\mathbf{q}+\sum_{\alpha\in f^{-1}({\dagger})\backslash
{\dagger}}\partial_{\mathbf{p}}A_{\alpha}(\mathbf{p}_\alpha);
s\bigg)\\
&\quad\mapsto\bigg(\bigg(\bigoplus_{j_k\in
f^{-1}(k)}A_{k,j_k}, \sum_{j_k\in
f^{-1}(k)}\partial_\mathbf{p}
A_{k,j_k}(\mathbf{p}_{k,j_k}), t_k\bigg)_{k\in \langle
m\rangle^\circ}, \\ &\qquad A+\sum_{\alpha\in
f^{-1}({\dagger})\backslash{\dagger}}A_\alpha,
\mathbf{q}+\sum_{\alpha\in f^{-1}({\dagger})\backslash
{\dagger}}\partial_{\mathbf{p}}A_{\alpha}(\mathbf{p}_\alpha),
\mathbf{q}+\sum_{\alpha\in f^{-1}({\dagger})\backslash
{\dagger}}\partial_{\mathbf{p}}A_{\alpha}(\mathbf{p}_\alpha),
s+\sum_{\alpha\in
f^{-1}({\dagger})\backslash{\dagger}}A_\alpha(\mathbf{p}_\alpha)\bigg).
\end{align*}
\begin{align*}
&\bigg(\bigg((A_{k,j_k})_{j_k\in f^{-1}(k)}; \sum_{j_k\in
f^{-1}(k)}\partial_\mathbf{p}
A_{k,j_k}(\mathbf{p}_{k,j_k}), t_k\bigg)_{k\in \langle
m\rangle^\circ}, \\ &\qquad (A_\alpha)_{\alpha\in
f^{-1}({\dagger})\backslash {\dagger}}; A, \mathbf{q},
\mathbf{q}+\sum_{\alpha\in f^{-1}({\dagger})\backslash
{\dagger}}\partial_{\mathbf{p}}A_{\alpha}(\mathbf{p}_\alpha);
s\bigg)\\
&\quad\mapsto\bigg(\bigg(\bigoplus_{j_k\in
f^{-1}(k)}A_{k,j_k}, \sum_{j_k\in
f^{-1}(k)}\partial_\mathbf{p}
A_{k,j_k}(\mathbf{p}_{k,j_k}), t_k\bigg)_{k\in \langle
m\rangle^\circ}, \\ &\qquad A+\sum_{\alpha\in
f^{-1}({\dagger})\backslash{\dagger}}A_\alpha,
\mathbf{q}+\sum_{\alpha\in f^{-1}({\dagger})\backslash
{\dagger}}\partial_{\mathbf{p}}A_{\alpha}(\mathbf{p}_\alpha),
\mathbf{q}+\sum_{\alpha\in f^{-1}({\dagger})\backslash
{\dagger}}\partial_{\mathbf{p}}A_{\alpha}(\mathbf{p}_\alpha),
s+\sum_{\alpha\in
f^{-1}({\dagger})\backslash{\dagger}}A_\alpha(\mathbf{p}_\alpha)\bigg).
\end{align*}
It is then straightforward to see that the diagram is Cartesian.
Let
Let ![]() $(F_NQ^0_M)^{\bullet,{\dagger} }$ be the free
$(F_NQ^0_M)^{\bullet,{\dagger} }$ be the free ![]() $VG^\bullet _{N}$-module generated by
$VG^\bullet _{N}$-module generated by ![]() $Q^0_M$. By the universal property of free modules, a
$Q^0_M$. By the universal property of free modules, a ![]() $VG_{N}^\bullet$-module homomorphism from
$VG_{N}^\bullet$-module homomorphism from ![]() $(FQ^0_M)^{\bullet,{\dagger} }$ to
$(FQ^0_M)^{\bullet,{\dagger} }$ to ![]() $\widehat {Q}_{N,M}^{\bullet,{\dagger} }$ is determined by a morphism
$\widehat {Q}_{N,M}^{\bullet,{\dagger} }$ is determined by a morphism ![]() $Q^0_M\rightarrow \widehat {Q}_{N,M}^{\langle 0\rangle _{\dagger} }$ in
$Q^0_M\rightarrow \widehat {Q}_{N,M}^{\langle 0\rangle _{\dagger} }$ in ![]() $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})$. Let
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})$. Let
denote the ![]() $VG_{N}^\bullet$-module homomorphism corresponding to the 1-morphism
$VG_{N}^\bullet$-module homomorphism corresponding to the 1-morphism

where the horizontal map is the identity map and the vertical map is the natural embedding of the connected component of ![]() $\widehat {Q}_{N,M}^{\langle 0\rangle _{\dagger} }$ defined by
$\widehat {Q}_{N,M}^{\langle 0\rangle _{\dagger} }$ defined by ![]() $A=0$ (the unit of the commutative algebra
$A=0$ (the unit of the commutative algebra ![]() $VG_{N}^\bullet$). In particular, on the underlying module we have
$VG_{N}^\bullet$). In particular, on the underlying module we have
 \begin{align} (F_NQ^0_M)^{\langle 0\rangle_{\dagger}}=VG_N^{\langle 0\rangle_{\dagger}}\times Q_M^0&\longrightarrow \widehat{Q}_{N,M}^{\langle 0\rangle_{\dagger}}\\ (A,\partial_{\mathbf{p}}A(\mathbf{p}); \mathbf{q},s)&\mapsto (A, \mathbf{q}+\partial_{\mathbf{p}}A(\mathbf{p}), \mathbf{q}+\partial_{\mathbf{p}}A(\mathbf{p}), s+A(\mathbf{p})). \nonumber \end{align}
\begin{align} (F_NQ^0_M)^{\langle 0\rangle_{\dagger}}=VG_N^{\langle 0\rangle_{\dagger}}\times Q_M^0&\longrightarrow \widehat{Q}_{N,M}^{\langle 0\rangle_{\dagger}}\\ (A,\partial_{\mathbf{p}}A(\mathbf{p}); \mathbf{q},s)&\mapsto (A, \mathbf{q}+\partial_{\mathbf{p}}A(\mathbf{p}), \mathbf{q}+\partial_{\mathbf{p}}A(\mathbf{p}), s+A(\mathbf{p})). \nonumber \end{align}
Let ![]() $\pi _{N,M}: \widehat {Q}^{\langle 0\rangle _{\dagger} }_{N,M}\rightarrow G_N$ be the obvious projection.
$\pi _{N,M}: \widehat {Q}^{\langle 0\rangle _{\dagger} }_{N,M}\rightarrow G_N$ be the obvious projection.
The following statement is an immediate consequence of Lemma 4.5.
Lemma 4.7 The map (4.1.7) is a fiber bundle on each component of ![]() $\widehat {Q}_{N,M}^{\langle 0\rangle _{\dagger} }$ isomorphic to the pullback bundle
$\widehat {Q}_{N,M}^{\langle 0\rangle _{\dagger} }$ isomorphic to the pullback bundle ![]() $\pi _{N,M}^{-1}VG_N$.
$\pi _{N,M}^{-1}VG_N$.
4.1.2 Stabilization of the local system categories of  $G_{N}$,
$G_{N}$,  $VG_N$ and
$VG_N$ and  $\widehat {Q}_{N,M}$
$\widehat {Q}_{N,M}$
Lemma 4.8
(a) The inductive system of
 $\mathrm {Fin}_*$-objects in
$\mathrm {Fin}_*$-objects in  $\mathrm {S}_{\mathrm {LCH}}$
for
$\mathrm {S}_{\mathrm {LCH}}$
for
 $X_0=VG, X_1=G$ determines a functor
$X_0=VG, X_1=G$ determines a functor
 \[ X: \Delta^1\times \mathbf{N}^{\rm op}\rightarrow \mathrm{CAlg}(\mathrm{Corr}(\mathrm{S}_{\mathrm{LCH}})_{\mathsf{fib},\mathsf{all}}). \]
\[ X: \Delta^1\times \mathbf{N}^{\rm op}\rightarrow \mathrm{CAlg}(\mathrm{Corr}(\mathrm{S}_{\mathrm{LCH}})_{\mathsf{fib},\mathsf{all}}). \]
(b) The inductive system of
 $I_{\pi _{\dagger} }$-objects over
$I_{\pi _{\dagger} }$-objects over  $(\mathbf {N}\times \mathbf {N})^{\geq \mathrm {dgnl}}$ in
$(\mathbf {N}\times \mathbf {N})^{\geq \mathrm {dgnl}}$ in  $\mathrm {S}_{\mathrm {LCH}}$
for
$\mathrm {S}_{\mathrm {LCH}}$
for
 $(X,Y)=(G, FQ^0), (VG, FQ^0), (VG, \widehat {Q})$ (where
$(X,Y)=(G, FQ^0), (VG, FQ^0), (VG, \widehat {Q})$ (where  $FQ^0$ means the corresponding free module generated by
$FQ^0$ means the corresponding free module generated by  $Q^0_M$) defines a functor
$Q^0_M$) defines a functor
 \[ (X_\clubsuit, Y_{\clubsuit, \spadesuit}): ((\mathbf{N}\times\mathbf{N})^{\geq \mathrm{dgnl}})^{\rm op} \rightarrow \mathcal{M}\mathrm{od}^{N(\mathrm{Fin}_*)}(\mathrm{Corr}(\mathrm{S}_{\mathrm{LCH}})_{\mathsf{fib},\mathsf{all}}). \]
\[ (X_\clubsuit, Y_{\clubsuit, \spadesuit}): ((\mathbf{N}\times\mathbf{N})^{\geq \mathrm{dgnl}})^{\rm op} \rightarrow \mathcal{M}\mathrm{od}^{N(\mathrm{Fin}_*)}(\mathrm{Corr}(\mathrm{S}_{\mathrm{LCH}})_{\mathsf{fib},\mathsf{all}}). \]
By Lemma 4.8, after applying the symmetric monoidal functor
we can form the limit in ![]() $\mathrm {CAlg}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$:
$\mathrm {CAlg}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$:
for ![]() $X=G, VG$. Similarly, we can form the limit in
$X=G, VG$. Similarly, we can form the limit in ![]() $\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$
$\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$
for ![]() $(X,Y)=(G,FQ^0),\ (VG, FQ^0),\ (VG, \widehat {Q}),$
$(X,Y)=(G,FQ^0),\ (VG, FQ^0),\ (VG, \widehat {Q}),$
Note that for ![]() $X=G, VG$,
$X=G, VG$,
gives a commutative algebra object in ![]() $\mathcal {S}\mathrm {pc}$ (here only the homotopy type is relevant), so under the natural symmetric monoidal functor
$\mathcal {S}\mathrm {pc}$ (here only the homotopy type is relevant), so under the natural symmetric monoidal functor ![]() $\mathrm {Loc}\mathrm {Sp}_!: \mathcal {S}\mathrm {pc}\rightarrow \mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$, the local system category
$\mathrm {Loc}\mathrm {Sp}_!: \mathcal {S}\mathrm {pc}\rightarrow \mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}}$, the local system category ![]() $\mathrm {Loc}(X,\mathrm {Sp})$ carries a natural symmetric monoidal structure, denoted by
$\mathrm {Loc}(X,\mathrm {Sp})$ carries a natural symmetric monoidal structure, denoted by ![]() $\mathrm {Loc}(X;\mathrm {Sp})^{\otimes _c}$. Since for any active map
$\mathrm {Loc}(X;\mathrm {Sp})^{\otimes _c}$. Since for any active map ![]() $f: \langle m\rangle \rightarrow \langle n\rangle$ in
$f: \langle m\rangle \rightarrow \langle n\rangle$ in ![]() $N(\mathrm {Fin}_*)$, the morphism
$N(\mathrm {Fin}_*)$, the morphism
is a proper locally trivial fibration for both ![]() $X=G, VG$, the symmetric monoidal structure on
$X=G, VG$, the symmetric monoidal structure on ![]() $\mathrm {Loc}(X;\mathrm {Sp})^{\otimes _*^!}$ agrees with that on
$\mathrm {Loc}(X;\mathrm {Sp})^{\otimes _*^!}$ agrees with that on ![]() $\mathrm {Loc}(X;\mathrm {Sp})^{\otimes _c}$. Indeed, this is a direct consequence of Proposition A.22. By restricting to the full subcategories of vector bundles of rank
$\mathrm {Loc}(X;\mathrm {Sp})^{\otimes _c}$. Indeed, this is a direct consequence of Proposition A.22. By restricting to the full subcategories of vector bundles of rank ![]() $0$ and composing with the natural functor
$0$ and composing with the natural functor ![]() $(\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}//}\to \mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}}$, we get a commutative diagram from (A.3.11):
$(\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}//}\to \mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}}$, we get a commutative diagram from (A.3.11):

where all functors are symmetric monoidal. Now using Step 2 in the proof of Proposition 4.13 (from Appendix A.4), both ![]() $X=G,VG$ give commutative algebra objects in
$X=G,VG$ give commutative algebra objects in ![]() $\mathrm {Corr}(\mathrm {Top})_{\mathsf {propfib}, \mathsf {all}}$ and
$\mathrm {Corr}(\mathrm {Top})_{\mathsf {propfib}, \mathsf {all}}$ and ![]() $\mathrm {Corr}(\mathcal {S}\mathrm {pc})_{\mathsf {hpf}', \mathsf {all}}$. As objects in the latter, both lie in the essential image of
$\mathrm {Corr}(\mathcal {S}\mathrm {pc})_{\mathsf {hpf}', \mathsf {all}}$. As objects in the latter, both lie in the essential image of ![]() $\mathrm {CAlg}(\mathcal {S}\mathrm {pc}_{\mathsf {hpf}'})\to \mathrm {CAlg}(\mathrm {Corr}(\mathcal {S}\mathrm {pc})_{\mathsf {hpf}',\mathsf {all}})$, corresponding to the classical commutative topological monoid structure on
$\mathrm {CAlg}(\mathcal {S}\mathrm {pc}_{\mathsf {hpf}'})\to \mathrm {CAlg}(\mathrm {Corr}(\mathcal {S}\mathrm {pc})_{\mathsf {hpf}',\mathsf {all}})$, corresponding to the classical commutative topological monoid structure on ![]() $G$ (
$G$ (![]() $VG\simeq G$ in
$VG\simeq G$ in ![]() $\mathrm {CAlg}(\mathcal {S}\mathrm {pc}^\times )$). Then the above claim about
$\mathrm {CAlg}(\mathcal {S}\mathrm {pc}^\times )$). Then the above claim about
follows.
Proposition 4.9 The commutative diagram over ![]() $(\mathbf {N}\times \mathbf {N})^{\geq \mathrm {dgnl}}\times \Delta ^2$
$(\mathbf {N}\times \mathbf {N})^{\geq \mathrm {dgnl}}\times \Delta ^2$

in ![]() $\mathrm {Fun}(N(\mathrm {Fin}_{*,{\dagger} }), \mathrm {S}_{\mathrm {LCH}})$ determines a functor
$\mathrm {Fun}(N(\mathrm {Fin}_{*,{\dagger} }), \mathrm {S}_{\mathrm {LCH}})$ determines a functor
 \begin{align*} F_{\psi}: &((\mathbf{N}\times \mathbf{N})^{\geq\mathrm{dgnl}})^{\rm op}\times \Delta^1\rightarrow \mathcal{M}\mathrm{od}^{N(\mathrm{Fin}_*)}(\mathrm{Corr}(\mathrm{S}_{\mathrm{LCH}})_{\mathsf{fib},\mathsf{all}})\\ &(N,M; 0)\mapsto (VG^\bullet_{N}, (F_NQ_M^0)^{\bullet,{\dagger}})\\ &(N,M;1)\mapsto (VG^\bullet_{N}, \widehat{Q}^{\bullet,{\dagger}}_{N,M}). \end{align*}
\begin{align*} F_{\psi}: &((\mathbf{N}\times \mathbf{N})^{\geq\mathrm{dgnl}})^{\rm op}\times \Delta^1\rightarrow \mathcal{M}\mathrm{od}^{N(\mathrm{Fin}_*)}(\mathrm{Corr}(\mathrm{S}_{\mathrm{LCH}})_{\mathsf{fib},\mathsf{all}})\\ &(N,M; 0)\mapsto (VG^\bullet_{N}, (F_NQ_M^0)^{\bullet,{\dagger}})\\ &(N,M;1)\mapsto (VG^\bullet_{N}, \widehat{Q}^{\bullet,{\dagger}}_{N,M}). \end{align*}
By Proposition 4.9 and passing to ![]() $\mathcal {M}\mathrm {od}^{N( \mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$ through
$\mathcal {M}\mathrm {od}^{N( \mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$ through ![]() $\mathrm {Loc}_*^!$, we have an isomorphism (using Lemma 4.7 again)
$\mathrm {Loc}_*^!$, we have an isomorphism (using Lemma 4.7 again)
4.2 The  $J$-homomorphism and quantization result
$J$-homomorphism and quantization result
Recall that the correspondence (4.1.6) induces a ![]() $VG_N^\bullet$-module homomorphism in the category
$VG_N^\bullet$-module homomorphism in the category ![]() $\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}})$ from the free module generated by
$\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}})$ from the free module generated by ![]() $Q_M^0$, denoted by
$Q_M^0$, denoted by ![]() $(F_NQ_M)^{\bullet,{\dagger} }$, to the module
$(F_NQ_M)^{\bullet,{\dagger} }$, to the module ![]() $\widehat {Q}_{N,M}^{\bullet,{\dagger} }$. We rewrite the resulting isomorphism (4.1.11) in
$\widehat {Q}_{N,M}^{\bullet,{\dagger} }$. We rewrite the resulting isomorphism (4.1.11) in ![]() $\mathcal {M}\mathrm {od}^{N( \mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$ as follows:
$\mathcal {M}\mathrm {od}^{N( \mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$ as follows:
 \begin{align*} F_{Q^0}: (\mathrm{Loc}(VG;\mathrm{Sp})^{\otimes_c}, \mathrm{Loc}(VG;\mathrm{Sp})\otimes \mathrm{Loc}(Q^0;\mathrm{Sp}))&\overset{\sim}{\longrightarrow} (\mathrm{Loc}(VG;\mathrm{Sp})^{\otimes_c}, \mathrm{Loc}(\widehat{Q};\mathrm{Sp}))\\ \mathcal{F}\otimes \mathcal{R}&\mapsto \psi_*(\mathcal{F}\boxtimes \mathcal{R}) \end{align*}
\begin{align*} F_{Q^0}: (\mathrm{Loc}(VG;\mathrm{Sp})^{\otimes_c}, \mathrm{Loc}(VG;\mathrm{Sp})\otimes \mathrm{Loc}(Q^0;\mathrm{Sp}))&\overset{\sim}{\longrightarrow} (\mathrm{Loc}(VG;\mathrm{Sp})^{\otimes_c}, \mathrm{Loc}(\widehat{Q};\mathrm{Sp}))\\ \mathcal{F}\otimes \mathcal{R}&\mapsto \psi_*(\mathcal{F}\boxtimes \mathcal{R}) \end{align*}
in which ![]() $\mathrm {Loc}(VG\times Q_0;\mathrm {Sp})\simeq \mathrm {Loc}(VG;\mathrm {Sp})\otimes \mathrm {Loc}(Q^0;\mathrm {Sp})$ is represented as the free module of
$\mathrm {Loc}(VG\times Q_0;\mathrm {Sp})\simeq \mathrm {Loc}(VG;\mathrm {Sp})\otimes \mathrm {Loc}(Q^0;\mathrm {Sp})$ is represented as the free module of ![]() $\mathrm {Loc}(VG;\mathrm {Sp})^{\otimes _c}$ generated by
$\mathrm {Loc}(VG;\mathrm {Sp})^{\otimes _c}$ generated by ![]() $\mathrm {Loc}(Q^0;\mathrm {Sp})$.
$\mathrm {Loc}(Q^0;\mathrm {Sp})$.
Let
be the obvious (open) inclusions. Let
be the natural equivalence induced from applying ![]() $\mathrm {Loc}^!_*$ to Lemma 4.8(a), taking horizontal inverse limits, and using (4.1.9). Consider the following diagram of objects in
$\mathrm {Loc}^!_*$ to Lemma 4.8(a), taking horizontal inverse limits, and using (4.1.9). Consider the following diagram of objects in ![]() $\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$.
$\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$.

The composition ![]() $\Phi _{Q}:=(j_{\widehat {Q}})^{-1}\circ F_{Q^0}\circ (p_*)^{-1}\circ j^!_{Q^0}$ is an equivalence in
$\Phi _{Q}:=(j_{\widehat {Q}})^{-1}\circ F_{Q^0}\circ (p_*)^{-1}\circ j^!_{Q^0}$ is an equivalence in ![]() $\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$. Moreover, we have the following.
$\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$. Moreover, we have the following.
Lemma 4.10 The equivalence ![]() $\Phi _Q$ on the underlying module category
$\Phi _Q$ on the underlying module category ![]() $\mathrm {Loc}(G\times \varinjlim _{M}\mathbf {R}^M\times \mathbf {R};\mathrm {Sp})$ is canonically homotopy equivalent to the identity functor.
$\mathrm {Loc}(G\times \varinjlim _{M}\mathbf {R}^M\times \mathbf {R};\mathrm {Sp})$ is canonically homotopy equivalent to the identity functor.
Proof. Consider the diagram

where ![]() $p_{N,M}$ is the natural projection and
$p_{N,M}$ is the natural projection and ![]() $\widetilde {\psi }_{N,M}$ is defined in the same way as
$\widetilde {\psi }_{N,M}$ is defined in the same way as ![]() $\psi _{N,M}$ above. To show the claim, we just need to show that the functor
$\psi _{N,M}$ above. To show the claim, we just need to show that the functor ![]() $(p_{N,M})_*$ is canonically isomorphic to
$(p_{N,M})_*$ is canonically isomorphic to ![]() $(\widetilde {\psi }_{N,M})_*$, that is compatible with
$(\widetilde {\psi }_{N,M})_*$, that is compatible with ![]() $N,M$. Let
$N,M$. Let
 \begin{align*} \widetilde{\Psi}_{N,M}: &[0,1]\times VG_N\times \mathbf{R}^M\times \mathbf{R}\rightarrow [0,1]\times G_N\times \mathbf{R}^M\times \mathbf{R}\\ &(\alpha, A,\mathbf{p}, \mathbf{q}, t)\mapsto (\alpha, A, \mathbf{q}+2\alpha\mathbf{p}, t+\alpha^2 |\mathbf{p}|^2). \end{align*}
\begin{align*} \widetilde{\Psi}_{N,M}: &[0,1]\times VG_N\times \mathbf{R}^M\times \mathbf{R}\rightarrow [0,1]\times G_N\times \mathbf{R}^M\times \mathbf{R}\\ &(\alpha, A,\mathbf{p}, \mathbf{q}, t)\mapsto (\alpha, A, \mathbf{q}+2\alpha\mathbf{p}, t+\alpha^2 |\mathbf{p}|^2). \end{align*}
Then ![]() $\widetilde {\Phi }_{N,M}$ gives an equivalence between the local system categories, whose restriction to
$\widetilde {\Phi }_{N,M}$ gives an equivalence between the local system categories, whose restriction to ![]() $\alpha =0,1$ are
$\alpha =0,1$ are ![]() $(p_{N,M})_*$ and
$(p_{N,M})_*$ and ![]() $(\widetilde {\psi }_{N,M})_*$, respectively, and this induces the canonical isomorphism between the two functors.
$(\widetilde {\psi }_{N,M})_*$, respectively, and this induces the canonical isomorphism between the two functors.
In summary, we have the following result.
Proposition 4.11 There is a natural equivalence in ![]() $\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$
$\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$
which induces the identity functor on the common underlying module category ![]() $\mathrm {Loc}(\widehat {Q};\mathrm {Sp})$.
$\mathrm {Loc}(\widehat {Q};\mathrm {Sp})$.
4.2.1 An equivalent model of the  $J$-homomorphism
$J$-homomorphism
We state a well-known result (cf. [Reference GlasmanGla16, Proposition 2.12]).
Proposition 4.12 For any ![]() $K^{\otimes }\in \mathrm {CAlg}(\mathcal {S}\mathrm {pc}^\times )$, we have a natural equivalence
$K^{\otimes }\in \mathrm {CAlg}(\mathcal {S}\mathrm {pc}^\times )$, we have a natural equivalence
 \begin{align} \mathrm{CAlg}(\mathrm{Loc}(K;\mathrm{Sp})^{\otimes_c})&\overset{\sim}{\rightarrow} \mathrm{Fun}^{\mathrm{R}\text{-}\mathrm{lax}}(K^{\otimes},\mathrm{Sp}^{\otimes})\\ \mathcal{F}&\mapsto (x\mapsto \iota_x^!\mathcal{F}). \nonumber \end{align}
\begin{align} \mathrm{CAlg}(\mathrm{Loc}(K;\mathrm{Sp})^{\otimes_c})&\overset{\sim}{\rightarrow} \mathrm{Fun}^{\mathrm{R}\text{-}\mathrm{lax}}(K^{\otimes},\mathrm{Sp}^{\otimes})\\ \mathcal{F}&\mapsto (x\mapsto \iota_x^!\mathcal{F}). \nonumber \end{align}In the Appendix (Corollary A.24), we give a proof of a weaker version of the proposition using the formalism of adjoint functors. Since we are not trying to compare the equivalence (4.2.2) with the weaker version from Corollary A.24, we will use the latter throughout the paper.
Let ![]() $\varpi _{VG}$ be the commutative algebra object in
$\varpi _{VG}$ be the commutative algebra object in ![]() $\mathrm {Loc}(VG;\mathrm {Sp})^{\otimes _c,!}$ that corresponds to the symmetric monoidal functor
$\mathrm {Loc}(VG;\mathrm {Sp})^{\otimes _c,!}$ that corresponds to the symmetric monoidal functor
where the latter map takes ![]() $\mathit {pt}^{\otimes }$ to the monoidal unit, the sphere spectrum.
$\mathit {pt}^{\otimes }$ to the monoidal unit, the sphere spectrum.
Proposition 4.13 Under the natural equivalence
the commutative algebra object ![]() $p_*\varpi _{VG}$ corresponds to the
$p_*\varpi _{VG}$ corresponds to the ![]() $J$-homomorphism
$J$-homomorphism
through (A.4.4).
The proposition is proved in Appendix A.4.
4.2.2 Twisted equivariant local systems
For any ![]() $H^\otimes \in \mathrm {CAlg}(\mathcal {S}\mathrm {pc}^\times )$ and
$H^\otimes \in \mathrm {CAlg}(\mathcal {S}\mathrm {pc}^\times )$ and ![]() $X\in \mathcal {S}\mathrm {pc}$ an
$X\in \mathcal {S}\mathrm {pc}$ an ![]() $H$-module, we have
$H$-module, we have ![]() $\mathrm {Loc}(X;\mathrm {Sp})$ a
$\mathrm {Loc}(X;\mathrm {Sp})$ a ![]() $\mathrm {Loc}(H;\mathrm {Sp})^{\otimes _c}$-module. Let
$\mathrm {Loc}(H;\mathrm {Sp})^{\otimes _c}$-module. Let ![]() $a: H\times X\rightarrow X$ denote the action map. We call any object in
$a: H\times X\rightarrow X$ denote the action map. We call any object in ![]() $\mathrm {Fun}(H^\otimes, \mathrm {Pic}(\mathbf {S})^\otimes )$ a character of
$\mathrm {Fun}(H^\otimes, \mathrm {Pic}(\mathbf {S})^\otimes )$ a character of ![]() $H$ (in
$H$ (in ![]() $\mathbf {S}$-lines).
$\mathbf {S}$-lines).
Definition 4.14 For any ![]() $\chi \in \mathrm {Fun}(H^\otimes, \mathrm {Pic}(\mathbf {S})^\otimes )$, we define
$\chi \in \mathrm {Fun}(H^\otimes, \mathrm {Pic}(\mathbf {S})^\otimes )$, we define ![]() $\mathrm {Loc}(X;\mathrm {Sp})^{\chi }$ to be the full (stable) subcategory of
$\mathrm {Loc}(X;\mathrm {Sp})^{\chi }$ to be the full (stable) subcategory of ![]() $\mathrm {Mod}_{\chi }(\mathrm {Loc}(X;\mathrm {Sp}))$ consisting of
$\mathrm {Mod}_{\chi }(\mathrm {Loc}(X;\mathrm {Sp}))$ consisting of ![]() $\chi$-modules
$\chi$-modules ![]() $\mathcal {L}$ satisfying that the structure map
$\mathcal {L}$ satisfying that the structure map
is an equivalence in ![]() $\mathrm {Loc}(H\times X;\mathrm {Sp})$. We call any object in
$\mathrm {Loc}(H\times X;\mathrm {Sp})$. We call any object in ![]() $\mathrm {Loc}(X;\mathrm {Sp})^{\chi }$ a
$\mathrm {Loc}(X;\mathrm {Sp})^{\chi }$ a ![]() $\chi$-equivariant local system on
$\chi$-equivariant local system on ![]() $X$.
$X$.
Lemma 4.15 If ![]() $X\simeq H$ is an
$X\simeq H$ is an ![]() $H$-torsor, i.e. the free module of
$H$-torsor, i.e. the free module of ![]() $H$ generated by a point, then there is a natural equivalence between the (stable
$H$ generated by a point, then there is a natural equivalence between the (stable ![]() $\infty$-)category of
$\infty$-)category of ![]() $\chi$-equivariant local systems on
$\chi$-equivariant local systems on ![]() $X$ and the category of local systems on a point, i.e.
$X$ and the category of local systems on a point, i.e. ![]() $\mathrm {Sp}$, via
$\mathrm {Sp}$, via
 \begin{align*} &\mathrm{Loc}(\mathit{pt};\mathrm{Sp})\rightarrow \mathrm{Loc}(X;\mathrm{Sp})^{\chi},\\ &\mathcal{R}\mapsto \chi\underset{\mathbf{S}}{\otimes}\mathcal{R}, \end{align*}
\begin{align*} &\mathrm{Loc}(\mathit{pt};\mathrm{Sp})\rightarrow \mathrm{Loc}(X;\mathrm{Sp})^{\chi},\\ &\mathcal{R}\mapsto \chi\underset{\mathbf{S}}{\otimes}\mathcal{R}, \end{align*}
whose inverse is pullback along the inclusion ![]() $\iota _{\mathit {pt}}: \mathit {pt}\hookrightarrow X$ that exhibits
$\iota _{\mathit {pt}}: \mathit {pt}\hookrightarrow X$ that exhibits ![]() $X$ as a free
$X$ as a free ![]() $H$-module.
$H$-module.
Proof. First, consider the sequence of ![]() $H$-module maps
$H$-module maps
which exhibits ![]() $X$ as an
$X$ as an ![]() $H$-torsor. Given a
$H$-torsor. Given a ![]() $\chi$-equivariant local system
$\chi$-equivariant local system ![]() $\mathcal {M}$ on
$\mathcal {M}$ on ![]() $H$, from definition, we have
$H$, from definition, we have
which implies that ![]() $\mathcal {M}$ is isomorphic to
$\mathcal {M}$ is isomorphic to ![]() $\chi \otimes _{\mathbf {S}}\mathcal {R}$ where
$\chi \otimes _{\mathbf {S}}\mathcal {R}$ where ![]() $\mathcal {R}$ is the costalk of
$\mathcal {R}$ is the costalk of ![]() $\mathcal {M}$ at the image of
$\mathcal {M}$ at the image of ![]() $\iota _{\mathit {pt}}$.
$\iota _{\mathit {pt}}$.
To see that
we use the results about free modules from [Reference LurieLur17, 4.2.4] (and [Reference LurieLur17, Corollary 4.5.1.6] for the equivalence to the commutative setting). Let ![]() $i_e: \{e\}\hookrightarrow H$ be the unity of
$i_e: \{e\}\hookrightarrow H$ be the unity of ![]() $H$ (up to a contractible space of choices), then
$H$ (up to a contractible space of choices), then ![]() $(i_{e})_!\mathbf {S}$ is the monoidal unity in
$(i_{e})_!\mathbf {S}$ is the monoidal unity in ![]() $\mathrm {Loc}(H;\mathrm {Sp})^{\otimes _c}$ (recall
$\mathrm {Loc}(H;\mathrm {Sp})^{\otimes _c}$ (recall ![]() $(i_{e})_!$ is the left adjoint of
$(i_{e})_!$ is the left adjoint of ![]() $(i_{e})^!$ on local system categories). Using
$(i_{e})^!$ on local system categories). Using ![]() $i_{\mathit {pt}}$, we identify
$i_{\mathit {pt}}$, we identify ![]() $\mathrm {Loc}(X;\mathrm {Sp})^\chi$ with
$\mathrm {Loc}(X;\mathrm {Sp})^\chi$ with ![]() $\mathrm {Loc}(H;\mathrm {Sp})^\chi$. Now
$\mathrm {Loc}(H;\mathrm {Sp})^\chi$. Now ![]() $\chi \in \mathrm {Loc}(H;\mathrm {Sp})$ is a free module of
$\chi \in \mathrm {Loc}(H;\mathrm {Sp})$ is a free module of ![]() $\chi$ generated by
$\chi$ generated by ![]() $(i_{e})_!\mathbf {S}$ in the sense of [Reference LurieLur17, Definition 4.2.4.1]. By
$(i_{e})_!\mathbf {S}$ in the sense of [Reference LurieLur17, Definition 4.2.4.1]. By ![]() $\mathbf {S}$-linearity,
$\mathbf {S}$-linearity, ![]() $\chi \otimes _{\mathbf {S}}\mathcal {R}$ is isomorphic to the free module generated by
$\chi \otimes _{\mathbf {S}}\mathcal {R}$ is isomorphic to the free module generated by ![]() $(i_e)_!\mathcal {R}$. Using [Reference LurieLur17, Corollary 4.2.4.6], we have
$(i_e)_!\mathcal {R}$. Using [Reference LurieLur17, Corollary 4.2.4.6], we have
 \begin{align*}
\mathrm{Hom}_{\mathrm{Loc}(H;\mathrm{Sp})^\chi}\Big(\chi\underset{\mathbf{S}}{\otimes}\mathcal{R}_1,
\chi\underset{\mathbf{S}}{\otimes}\mathcal{R}_2\Big)&\cong
\mathrm{Hom}_{\mathrm{Loc}(H;\mathrm{Sp})}\Big((i_e)_!\mathcal{R}_1,
\chi\underset{\mathbf{S}}{\otimes}\mathcal{R}_2\Big)\\
&\cong \mathrm{Hom}\Big(\mathcal{R}_1,
i_e^!\Big(\chi\underset{\mathbf{S}}{\otimes}\mathcal{R}_2\Big)\Big)\cong
\mathrm{Hom}(\mathcal{R}_1, \mathcal{R}_2).
\end{align*}
\begin{align*}
\mathrm{Hom}_{\mathrm{Loc}(H;\mathrm{Sp})^\chi}\Big(\chi\underset{\mathbf{S}}{\otimes}\mathcal{R}_1,
\chi\underset{\mathbf{S}}{\otimes}\mathcal{R}_2\Big)&\cong
\mathrm{Hom}_{\mathrm{Loc}(H;\mathrm{Sp})}\Big((i_e)_!\mathcal{R}_1,
\chi\underset{\mathbf{S}}{\otimes}\mathcal{R}_2\Big)\\
&\cong \mathrm{Hom}\Big(\mathcal{R}_1,
i_e^!\Big(\chi\underset{\mathbf{S}}{\otimes}\mathcal{R}_2\Big)\Big)\cong
\mathrm{Hom}(\mathcal{R}_1, \mathcal{R}_2).
\end{align*}
Then the lemma follows.
A direct consequence of Proposition 4.11 and the above identification of ![]() $J$ with
$J$ with ![]() $p_*\varpi _{VG}$ is the following.
$p_*\varpi _{VG}$ is the following.
Corollary 4.16
(a) For any
 $\mathbf {S}$-module
$\mathbf {S}$-module  $\mathcal {R}$, the local system
$\mathcal {R}$, the local system  $\psi _*(\varpi _{VG}\boxtimes \mathcal {R})\in \mathrm {Loc}(\widehat {Q};\mathrm {Sp})$ as an
$\psi _*(\varpi _{VG}\boxtimes \mathcal {R})\in \mathrm {Loc}(\widehat {Q};\mathrm {Sp})$ as an  $\varpi _{VG}$-module is corresponding to the
$\varpi _{VG}$-module is corresponding to the  $J$-equivariant local system
$J$-equivariant local system  $J\boxtimes \mathcal {R}$, under the natural equivalence
$J\boxtimes \mathcal {R}$, under the natural equivalence  $\Phi _Q$ (4.2.1).
$\Phi _Q$ (4.2.1).(b) The correspondence
induces a canonical equivalence through the functor
through the functor \[ \mathrm{Loc}(Q^0;\mathrm{Sp})\overset{\sim}{\longrightarrow} \mathrm{Loc}(\widehat{Q};\mathrm{Sp})^{J} \]
\[ \mathrm{Loc}(Q^0;\mathrm{Sp})\overset{\sim}{\longrightarrow} \mathrm{Loc}(\widehat{Q};\mathrm{Sp})^{J} \]
 $\psi _*\pi _{Q^0}^!$.
$\psi _*\pi _{Q^0}^!$.
Thus, we have achieved the desired quantization results on the Hamiltonian ![]() $\coprod _n BO(n)$-action on
$\coprod _n BO(n)$-action on ![]() $\varinjlim _NT^*\mathbf {R}^N$ and its ‘module’ generated by the stabilization of
$\varinjlim _NT^*\mathbf {R}^N$ and its ‘module’ generated by the stabilization of ![]() $L_0$: the Hamiltonian
$L_0$: the Hamiltonian ![]() $\coprod _n BO(n)$-action is canonically quantized by the dualizing sheaf
$\coprod _n BO(n)$-action is canonically quantized by the dualizing sheaf ![]() $\varpi _{VG}$ as a commutative algebra object in
$\varpi _{VG}$ as a commutative algebra object in ![]() $\mathrm {Loc}(VG;\mathrm {Sp})^{\otimes _c}$, and the ‘module’ generated by the stabilization of
$\mathrm {Loc}(VG;\mathrm {Sp})^{\otimes _c}$, and the ‘module’ generated by the stabilization of ![]() $L_0$ is quantized by the objects in the stable
$L_0$ is quantized by the objects in the stable ![]() $\infty$-category of
$\infty$-category of ![]() $J$-equivariant local systems on
$J$-equivariant local systems on ![]() $\widehat {Q}$.
$\widehat {Q}$.
5. Morse transformations and applications to stratified Morse theory
In this section, we introduce the notion of Morse transformations associated to a (germ of a) smooth conic Lagrangian, which is a special class of contact transformations that has intimate relation with stratified Morse functions. We give a classification of (stabilized) Morse transformations, then we apply the quantization results from the previous section to give an enrichment of the main theorem in stratified Morse theory by the ![]() $J$-homomorphism.
$J$-homomorphism.
5.1 Morse transformations
For any smooth manifold ![]() $X$, let
$X$, let ![]() $T^{*,<0}(X\times \mathbf {R}_t)$ denote the open half of
$T^{*,<0}(X\times \mathbf {R}_t)$ denote the open half of ![]() $T^*(X\times \mathbf {R}_{t_0})$ consisting of covectors whose components in
$T^*(X\times \mathbf {R}_{t_0})$ consisting of covectors whose components in ![]() $dt$ are strictly negative. Let
$dt$ are strictly negative. Let ![]() $T^{*,\geq 0}(X\times \mathbf {R}_{t_0})$ by its complement in
$T^{*,\geq 0}(X\times \mathbf {R}_{t_0})$ by its complement in ![]() $T^*(X\times \mathbf {R}_{t_0})$. We implicitly assume that all the geometric objects and maps are taken in an analytic-geometric category, e.g. we can assume that they are subanalytic. For an exact (connected) Lagrangian submanifold
$T^*(X\times \mathbf {R}_{t_0})$. We implicitly assume that all the geometric objects and maps are taken in an analytic-geometric category, e.g. we can assume that they are subanalytic. For an exact (connected) Lagrangian submanifold ![]() $L\subset T^*X$ (not necessarily closed), a conic Lagrangian lifting
$L\subset T^*X$ (not necessarily closed), a conic Lagrangian lifting ![]() $\mathbf {L}$ of
$\mathbf {L}$ of ![]() $L$ is a conic Lagrangian in
$L$ is a conic Lagrangian in ![]() $T^{*,<0}(X\times \mathbf {R}_t)$ such that its projection to
$T^{*,<0}(X\times \mathbf {R}_t)$ such that its projection to ![]() $T^*X$ is
$T^*X$ is ![]() $L$ and the 1-form
$L$ and the 1-form ![]() $-dt+\alpha |_{\mathbf {L}}$ vanishes. Note that the conic Lagrangian liftings of
$-dt+\alpha |_{\mathbf {L}}$ vanishes. Note that the conic Lagrangian liftings of ![]() $L$ are essentially unique up to a shift of a constant in the
$L$ are essentially unique up to a shift of a constant in the ![]() $t$-coordinate. Moreover, if the exact Lagrangian
$t$-coordinate. Moreover, if the exact Lagrangian ![]() $L$ is in general position, i.e. its projection to
$L$ is in general position, i.e. its projection to ![]() $X$ is finite-to-one, then any conic Lagrangian lifting
$X$ is finite-to-one, then any conic Lagrangian lifting ![]() $\mathbf {L}$ is determined by its front projection in
$\mathbf {L}$ is determined by its front projection in ![]() $X\times \mathbf {R}_t$, i.e. its image under the projection
$X\times \mathbf {R}_t$, i.e. its image under the projection ![]() $T^{*,<0}(X\times \mathbf {R}_t)\rightarrow X\times \mathbf {R}_t$ to the base. For example, if the front projection of
$T^{*,<0}(X\times \mathbf {R}_t)\rightarrow X\times \mathbf {R}_t$ to the base. For example, if the front projection of ![]() $\mathbf {L}$ is a smooth hypersurface, then
$\mathbf {L}$ is a smooth hypersurface, then ![]() $\mathbf {L}$ is just half of the conormal bundle of the hypersurface contained in
$\mathbf {L}$ is just half of the conormal bundle of the hypersurface contained in ![]() $T^{*,<0}(X\times \mathbf {R}_t)$, and we say it is the negative conormal bundle of the smooth hypersurface.
$T^{*,<0}(X\times \mathbf {R}_t)$, and we say it is the negative conormal bundle of the smooth hypersurface.
Let ![]() $(L,(0,p_0))$ be a germ of a smooth Lagrangian (in general position) in
$(L,(0,p_0))$ be a germ of a smooth Lagrangian (in general position) in ![]() $T^*\mathbf {R}^M$ with center
$T^*\mathbf {R}^M$ with center ![]() $(0,p_0)$ and let
$(0,p_0)$ and let ![]() $(\mathbf {L}, (0,p_0; t_0=0, -dt_0))$ be the germ of a conic Lagrangian lifting of
$(\mathbf {L}, (0,p_0; t_0=0, -dt_0))$ be the germ of a conic Lagrangian lifting of ![]() $(L,(0,p_0))$ in
$(L,(0,p_0))$ in ![]() $T^{*,<0}(\mathbf {R}^M\times \mathbf {R}_{t_0})$. Following [Reference Kashiwara and SchapiraKS94], a germ of a contact transformation with respect
$T^{*,<0}(\mathbf {R}^M\times \mathbf {R}_{t_0})$. Following [Reference Kashiwara and SchapiraKS94], a germ of a contact transformation with respect ![]() $(0,p_0; t_0=0, -dt_0)$ is a germ of a conic Lagrangian
$(0,p_0; t_0=0, -dt_0)$ is a germ of a conic Lagrangian ![]() $\mathbf {L}_{01}\subset (T^{*,<0}(\mathbf {R}^M\times \mathbf {R}_{t_0}))^-\times \mathring {T}^*(\mathbf {R}^M\times \mathbf {R}_{t_1})$ such that
$\mathbf {L}_{01}\subset (T^{*,<0}(\mathbf {R}^M\times \mathbf {R}_{t_0}))^-\times \mathring {T}^*(\mathbf {R}^M\times \mathbf {R}_{t_1})$ such that ![]() $\mathbf {L}_{01}$ induces a conic symplectomorphism from a germ of an open set in
$\mathbf {L}_{01}$ induces a conic symplectomorphism from a germ of an open set in ![]() $T^{*,<0}(\mathbf {R}^M\times \mathbf {R}_{t_0})$ centered at
$T^{*,<0}(\mathbf {R}^M\times \mathbf {R}_{t_0})$ centered at ![]() $(0,p_0; t_0=0, -dt_0)$ to a germ of an open set in
$(0,p_0; t_0=0, -dt_0)$ to a germ of an open set in ![]() $\mathring {T}^{*}(\mathbf {R}^M\times \mathbf {R}_{t_1})$, where
$\mathring {T}^{*}(\mathbf {R}^M\times \mathbf {R}_{t_1})$, where ![]() $\mathring {T}^*X$ means the cotangent bundle with the zero-section deleted for any
$\mathring {T}^*X$ means the cotangent bundle with the zero-section deleted for any ![]() $X$. In the following, any (conic) Lagrangian is understood as a germ of a (conic) Lagrangian, and any contact transformation is understood as a germ of a contact transformation, unless otherwise specified.
$X$. In the following, any (conic) Lagrangian is understood as a germ of a (conic) Lagrangian, and any contact transformation is understood as a germ of a contact transformation, unless otherwise specified.
It is proved in [Reference Kashiwara and SchapiraKS94] that there exists a contact transformation ![]() $\mathbf {L}_{01}$ such that
$\mathbf {L}_{01}$ such that ![]() $\mathbf {L}_{01}$ is locally the conormal bundle of a smooth hypersurface near the center, and it corresponds to a conic symplectomorphism which takes
$\mathbf {L}_{01}$ is locally the conormal bundle of a smooth hypersurface near the center, and it corresponds to a conic symplectomorphism which takes ![]() $(\mathbf {L},(0,p_0; t_0=0, -dt_0))$ to a conic Lagrangian that is locally the conormal bundle of a smooth hypersurface in
$(\mathbf {L},(0,p_0; t_0=0, -dt_0))$ to a conic Lagrangian that is locally the conormal bundle of a smooth hypersurface in ![]() $\mathbf {R}^M\times \mathbf {R}_{t_1}$. We call such a contact transformation a Morse transformation with respect to
$\mathbf {R}^M\times \mathbf {R}_{t_1}$. We call such a contact transformation a Morse transformation with respect to ![]() $(\mathbf {L}, (0,p_0; t_0=0, -dt_0))$. The space of Morse transformations form an open dense subset in the space of all contact transformations with respect to
$(\mathbf {L}, (0,p_0; t_0=0, -dt_0))$. The space of Morse transformations form an open dense subset in the space of all contact transformations with respect to ![]() $(0,p_0; t_0=0, -dt_0)$. There is an obvious action by the group of diffeomorphisms of
$(0,p_0; t_0=0, -dt_0)$. There is an obvious action by the group of diffeomorphisms of ![]() $\mathbf {R}^M\times \mathbf {R}_{t_1}$ on the space of Morse transformations.
$\mathbf {R}^M\times \mathbf {R}_{t_1}$ on the space of Morse transformations.
We state some useful facts about the space of Morse transformations modulo the action by ![]() $\mathrm {Diff}(\mathbf {R}^M\times \mathbf {R}_{t_1})$. We will assume that the germ
$\mathrm {Diff}(\mathbf {R}^M\times \mathbf {R}_{t_1})$. We will assume that the germ ![]() $(\mathbf {L},(0,p_0; t_0=0, -dt_0))$ is sent to a germ
$(\mathbf {L},(0,p_0; t_0=0, -dt_0))$ is sent to a germ ![]() $(\mathbf {L}_1, (0,p_1; t_1=0, -dt_1))$ in
$(\mathbf {L}_1, (0,p_1; t_1=0, -dt_1))$ in ![]() $T^{*,<0}(\mathbf {R}^M\times \mathbf {R}_{t_1})$ through
$T^{*,<0}(\mathbf {R}^M\times \mathbf {R}_{t_1})$ through ![]() $\mathbf {L}_{01}$. For any cotangent bundle involved, we let
$\mathbf {L}_{01}$. For any cotangent bundle involved, we let ![]() $\pi$ denote its projection to the base. Let
$\pi$ denote its projection to the base. Let ![]() $A_{L_{(0,p_0)}}$ be the quadratic form on
$A_{L_{(0,p_0)}}$ be the quadratic form on ![]() $\pi _*T_{(0,p_0)}L$ determined by the linear Lagrangian
$\pi _*T_{(0,p_0)}L$ determined by the linear Lagrangian ![]() $T_{(0,p_0)}L$ in
$T_{(0,p_0)}L$ in ![]() $T_{(0,p_0)}(T^*\mathbf {R}^M)$. We will equally view
$T_{(0,p_0)}(T^*\mathbf {R}^M)$. We will equally view ![]() $A_{L_{(0,p_0)}}$ as a quadratic form on
$A_{L_{(0,p_0)}}$ as a quadratic form on ![]() $\pi _*T_{(0,p_0; t_0=0, -dt_0)}\mathbf {L}$ as a linear subspace in
$\pi _*T_{(0,p_0; t_0=0, -dt_0)}\mathbf {L}$ as a linear subspace in ![]() $\mathbf {R}^M\times \mathbf {R}_{t_0}$.
$\mathbf {R}^M\times \mathbf {R}_{t_0}$.
Proposition 5.1
(a) The space of Morse transformations
 $\mathbf {L}_{01}$ with respect to
$\mathbf {L}_{01}$ with respect to  $(\mathbf {L}, (0,p_0; t_0=0, -dt_0))$ modulo the action of
$(\mathbf {L}, (0,p_0; t_0=0, -dt_0))$ modulo the action of  $\mathrm {Diff}(\mathbf {R}^M\times \mathbf {R}_{t_1})$ is canonically homotopy equivalent to the space of quadratic forms
$\mathrm {Diff}(\mathbf {R}^M\times \mathbf {R}_{t_1})$ is canonically homotopy equivalent to the space of quadratic forms  $A_S$ on
$A_S$ on  $\pi _*T_{(0,p_0)}L$ satisfying that
$\pi _*T_{(0,p_0)}L$ satisfying that  $A_S-A_{L_{(0,p_0)}}$ is non-degenerate.
$A_S-A_{L_{(0,p_0)}}$ is non-degenerate.(b) For each quadratic form
 $A_S$ as above, viewed as a quadratic form on
$A_S$ as above, viewed as a quadratic form on  $\pi _*T_{(0,p_0; t_0=0, -dt_0)}\mathbf {L}$ as well, it corresponds to a Morse transformation given by the negative conormal bundle (negative in
$\pi _*T_{(0,p_0; t_0=0, -dt_0)}\mathbf {L}$ as well, it corresponds to a Morse transformation given by the negative conormal bundle (negative in  $dt_1$) of
(5.1.1)where
$dt_1$) of
(5.1.1)where \begin{equation} t_1-t_0-p_1\cdot \mathbf{q}_1+p_0\cdot \mathbf{q}_0+\tfrac{1}{2}A_S(\mathbf{q}_0)-\mathbf{q}_0\cdot\mathbf{q}_1=0, \end{equation}
\begin{equation} t_1-t_0-p_1\cdot \mathbf{q}_1+p_0\cdot \mathbf{q}_0+\tfrac{1}{2}A_S(\mathbf{q}_0)-\mathbf{q}_0\cdot\mathbf{q}_1=0, \end{equation} $p_0,p_1$ are fixed and
$p_0,p_1$ are fixed and  $A_S(\mathbf {q}_0)$ is from extending by zero along the orthogonal complement of
$A_S(\mathbf {q}_0)$ is from extending by zero along the orthogonal complement of  $\pi _*T_{(0,p_0; t_0=0, -dt_0)}\mathbf {L}$ in
$\pi _*T_{(0,p_0; t_0=0, -dt_0)}\mathbf {L}$ in  $\mathbf {R}^M\times \mathbf {R}_{t_0}$.
$\mathbf {R}^M\times \mathbf {R}_{t_0}$.(c) For two (globally defined) quadratic forms
 $A_{S,1}$ and
$A_{S,1}$ and  $A_{S,2}$ on
$A_{S,2}$ on  $\mathbf {R}^M$, the negative conormal bundle of the hypersurface (5.1.1) for
$\mathbf {R}^M$, the negative conormal bundle of the hypersurface (5.1.1) for  $A_{S,i}$ determines a symplectomorphism
$A_{S,i}$ determines a symplectomorphism  $\Phi _i$ on
$\Phi _i$ on  $T^*\mathbf {R}^M$, respectively. Let
$T^*\mathbf {R}^M$, respectively. Let  $H_{12}(\mathbf {q}_1,\mathbf {p}_1)=\frac {1}{2}(A_{S,2}-A_{S,1})(\mathbf {p}_1-p_1)$ and
$H_{12}(\mathbf {q}_1,\mathbf {p}_1)=\frac {1}{2}(A_{S,2}-A_{S,1})(\mathbf {p}_1-p_1)$ and  $\varphi _{H_{12}}^1$ be the time-1 map of the Hamiltonian flow of
$\varphi _{H_{12}}^1$ be the time-1 map of the Hamiltonian flow of  $H_{12}$. Then
$H_{12}$. Then
 \[ \Phi_2=\varphi_{H_{12}}^1\circ\Phi_1. \]
\[ \Phi_2=\varphi_{H_{12}}^1\circ\Phi_1. \]
Proof. Since a germ of a contact transformation is determined by the tangent space of its center up to a contractible space of homotopies, parts (a) and (b) are linear problems and can be solved using a similar consideration as in the proof of [Reference Kashiwara and SchapiraKS94, Proposition A.2.6]. For the reader's convenience, we sketch the proof here.
Without loss of generality, we may reduce the case to ![]() $p_1=0$ and
$p_1=0$ and ![]() $p_0=0$. For the general case, we just need to apply an linear transformation
$p_0=0$. For the general case, we just need to apply an linear transformation ![]() $(\mathbf {q}_i, t_i)\mapsto (\mathbf {q}_i, t_i+p_i\cdot \mathbf {q}_i)$ for
$(\mathbf {q}_i, t_i)\mapsto (\mathbf {q}_i, t_i+p_i\cdot \mathbf {q}_i)$ for ![]() $i=0,1$. We fix a basis in
$i=0,1$. We fix a basis in ![]() $\mathbf {R}^M_{\mathbf {q}_0}$ (as a vector space) such that the first
$\mathbf {R}^M_{\mathbf {q}_0}$ (as a vector space) such that the first ![]() $s$ elements is the basis of
$s$ elements is the basis of ![]() $\pi _*T_{(0,0)}L$. Given any
$\pi _*T_{(0,0)}L$. Given any ![]() $\mathbf {L}_{01}$, the fixed basis in
$\mathbf {L}_{01}$, the fixed basis in ![]() $\mathbf {R}^M_{\mathbf {q}_0}$ together with the standard basis on
$\mathbf {R}^M_{\mathbf {q}_0}$ together with the standard basis on ![]() $\mathbf {R}_{t_0}$ determines a unique basis in
$\mathbf {R}_{t_0}$ determines a unique basis in ![]() $\mathbf {R}^M_{\mathbf {q}_1}\times \mathbf {R}_{t_1}$ (the projection to the cotangent base of both the image of the dual basis in
$\mathbf {R}^M_{\mathbf {q}_1}\times \mathbf {R}_{t_1}$ (the projection to the cotangent base of both the image of the dual basis in ![]() $(\mathbf {R}_{\mathbf {q}_0}^M)^*$ and the image of
$(\mathbf {R}_{\mathbf {q}_0}^M)^*$ and the image of ![]() $\partial _{t_0}$ under
$\partial _{t_0}$ under ![]() $\mathbf {L}_{01}$), with respect to which we can write down the tangent space of
$\mathbf {L}_{01}$), with respect to which we can write down the tangent space of ![]() $\mathbf {L}_{01}$ at
$\mathbf {L}_{01}$ at ![]() $(0, 0;t_0=0, dt_0; 0, 0;t_1=0, -dt_1)$ in the standard form as
$(0, 0;t_0=0, dt_0; 0, 0;t_1=0, -dt_1)$ in the standard form as
 \[ \left(\begin{array}{ccc|ccc|cc|ccc|ccc|cc} 1 & & & 0 & & & 0 & 0 & & & & & & & 0 & 0\\ & \ddots & & & \ddots & & \vdots & \vdots & & A & & & I & & \vdots & \vdots \\ & & 1 & & & 0 & 0 & 0 & & & & & & & 0 & 0\\ \hline\\ 0 & & & 1 & & & 0 & 0 & & & & & & & 0 & y_1 \\ & \ddots & & & \ddots & & \vdots & \vdots & & I & & & C & & \vdots & \vdots \\ & & 0 & & & 1 & 0 & 0 & & & & & & & 0 & y_M\\ \hline\\ 0 & \cdots & 0 & 0 & \cdots & 0 & 1 & 1 & 0 & \cdots & 0 & y_1 & \cdots & y_M & 0 & x\\ 0 & \cdots & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & \cdots & 0 & 1 & -1 \end{array}\right), \]
\[ \left(\begin{array}{ccc|ccc|cc|ccc|ccc|cc} 1 & & & 0 & & & 0 & 0 & & & & & & & 0 & 0\\ & \ddots & & & \ddots & & \vdots & \vdots & & A & & & I & & \vdots & \vdots \\ & & 1 & & & 0 & 0 & 0 & & & & & & & 0 & 0\\ \hline\\ 0 & & & 1 & & & 0 & 0 & & & & & & & 0 & y_1 \\ & \ddots & & & \ddots & & \vdots & \vdots & & I & & & C & & \vdots & \vdots \\ & & 0 & & & 1 & 0 & 0 & & & & & & & 0 & y_M\\ \hline\\ 0 & \cdots & 0 & 0 & \cdots & 0 & 1 & 1 & 0 & \cdots & 0 & y_1 & \cdots & y_M & 0 & x\\ 0 & \cdots & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 & 0 & \cdots & 0 & 1 & -1 \end{array}\right), \]
in which: (i) a basis of the tangent space is displayed in row vectors with respect to the chosen basis of ![]() $\mathbf {R}^M_{\mathbf {q}_0}, \mathbf {R}^M_{\mathbf {q}_1}, \mathbf {R}_{t_0}, \mathbf {R}_{t_1}$ (for
$\mathbf {R}^M_{\mathbf {q}_0}, \mathbf {R}^M_{\mathbf {q}_1}, \mathbf {R}_{t_0}, \mathbf {R}_{t_1}$ (for ![]() $\mathbf {R}_{t_i}$ we use the standard basis
$\mathbf {R}_{t_i}$ we use the standard basis ![]() $\partial _{t_i}$) and their respective dual basis in the dual vector spaces; (ii)
$\partial _{t_i}$) and their respective dual basis in the dual vector spaces; (ii) ![]() $A=A^T, C=C^T$ and
$A=A^T, C=C^T$ and ![]() $y_1,\ldots, y_M, x$ are arbitrary real numbers. The requirement on
$y_1,\ldots, y_M, x$ are arbitrary real numbers. The requirement on ![]() $(\mathbf {L}_1, (0,p_1;0,-dt_1))$ is exactly the condition that the top left
$(\mathbf {L}_1, (0,p_1;0,-dt_1))$ is exactly the condition that the top left ![]() $s\times s$-submatrix in the symmetric matrix
$s\times s$-submatrix in the symmetric matrix ![]() $A$ satisfies
$A$ satisfies ![]() $(A-A_{L_{(0,p_0)}})|_{\pi _*T_{(0,p_0)}L}$ is non-degenerate. Thus, the top left
$(A-A_{L_{(0,p_0)}})|_{\pi _*T_{(0,p_0)}L}$ is non-degenerate. Thus, the top left ![]() $s\times s$-submatrix in
$s\times s$-submatrix in ![]() $A$ exactly gives
$A$ exactly gives ![]() $A_S|_{\pi _*T_{(0,0)}L}$. Then part (a) follows directly. Part (b) follows from taking
$A_S|_{\pi _*T_{(0,0)}L}$. Then part (a) follows directly. Part (b) follows from taking ![]() $C=0$ and
$C=0$ and ![]() $y_1=\cdots =y_M=x=0$.
$y_1=\cdots =y_M=x=0$.
For part (c), if we write down the negative conormal of (5.1.1) explicitly,
then we see that it corresponds to the symplectomorphism on ![]() $T^*\mathbf {R}^M$ given by
$T^*\mathbf {R}^M$ given by
Thus, part (c) follows.
Note that when ![]() $p_0,p_1$ and
$p_0,p_1$ and ![]() $A_S(\mathbf {q}_0)$ are all zero, the contact transformation (5.1.1) gives the Fourier transform on
$A_S(\mathbf {q}_0)$ are all zero, the contact transformation (5.1.1) gives the Fourier transform on ![]() $T^*\mathbf {R}^M$.
$T^*\mathbf {R}^M$.
5.2 Relation to stratified Morse theory
There is a close relation between Morse transformations and stratified Morse functions (and their stabilizations) as follows. Now assume we are in the setting of § 1.3. Let ![]() $(x_0,\xi _0)\in \Lambda _{\mathfrak {S}}$ be a smooth point with
$(x_0,\xi _0)\in \Lambda _{\mathfrak {S}}$ be a smooth point with ![]() $\xi _0\neq 0$. If
$\xi _0\neq 0$. If ![]() $\xi _0=0$, we will embed
$\xi _0=0$, we will embed ![]() $X$ into
$X$ into ![]() $X\times \mathbf {R}$ by the graph of the constant function
$X\times \mathbf {R}$ by the graph of the constant function ![]() $0$ on
$0$ on ![]() $X$, and reduce the case to
$X$, and reduce the case to ![]() $\xi _0\neq 0$. Let
$\xi _0\neq 0$. Let ![]() $\mathbf {k}$ be any commutative ring spectrum.
$\mathbf {k}$ be any commutative ring spectrum.
5.2.1 Passing from local (stratified) Morse functions to  $\Omega$-lenses
$\Omega$-lenses
Recall in stratified Morse theory, to define the microlocal stalk at ![]() $(x_0,\xi _0)$, we choose a local Morse function
$(x_0,\xi _0)$, we choose a local Morse function ![]() $f$ in the following sense:
$f$ in the following sense: ![]() $f(x_0)=0$,
$f(x_0)=0$, ![]() $df_{x_0}=\xi _0$, and
$df_{x_0}=\xi _0$, and ![]() $f|_{S_0}$ is Morse at
$f|_{S_0}$ is Morse at ![]() $x_0$ (here
$x_0$ (here ![]() $S_0$ is the stratum containing
$S_0$ is the stratum containing ![]() $x_0$). In particular, the space of local Morse functions associated to
$x_0$). In particular, the space of local Morse functions associated to ![]() $(x_0,\xi _0)\in \Lambda _{\mathfrak {S}}^{\rm sm}$ is naturally homotopy equivalent to the space of non-degenerate quadratic forms on the tangent space
$(x_0,\xi _0)\in \Lambda _{\mathfrak {S}}^{\rm sm}$ is naturally homotopy equivalent to the space of non-degenerate quadratic forms on the tangent space ![]() $T_{x_0}S_0.$ Since
$T_{x_0}S_0.$ Since ![]() $\xi _0\neq 0$, using a subanalytic change of local coordinates, we identify an open neighborhood of
$\xi _0\neq 0$, using a subanalytic change of local coordinates, we identify an open neighborhood of ![]() $x_0$ with an open neighborhood of
$x_0$ with an open neighborhood of ![]() $U$ of
$U$ of ![]() $(0,0)$ in
$(0,0)$ in ![]() $\mathbf {R}^r\times \mathbf {R}_{t}$, where
$\mathbf {R}^r\times \mathbf {R}_{t}$, where ![]() $r=\dim X$, such that
$r=\dim X$, such that ![]() $f$ becomes the function
$f$ becomes the function ![]() $-t$ and
$-t$ and ![]() $\xi _0$ becomes
$\xi _0$ becomes ![]() $-dt$. In this way, an open neighborhood of
$-dt$. In this way, an open neighborhood of ![]() $(x_0,\xi _0)$ in
$(x_0,\xi _0)$ in ![]() $\Lambda _{\mathfrak {S}}$ is identified with an open neighborhood of
$\Lambda _{\mathfrak {S}}$ is identified with an open neighborhood of ![]() $(0,p=0;t=0, -dt)$ in a smooth conic Lagrangian in
$(0,p=0;t=0, -dt)$ in a smooth conic Lagrangian in ![]() $T^{*,<0}(\mathbf {R}^r\times \mathbf {R}_{t})$. Let
$T^{*,<0}(\mathbf {R}^r\times \mathbf {R}_{t})$. Let ![]() $H=\{t=0\}$, and let
$H=\{t=0\}$, and let ![]() $B_\delta ((x,t))$ be the standard open
$B_\delta ((x,t))$ be the standard open ![]() $\delta$-ball centered at
$\delta$-ball centered at ![]() $(x, t)$. Fix a Whitney stratification
$(x, t)$. Fix a Whitney stratification ![]() $\mathfrak {S}'$ of
$\mathfrak {S}'$ of ![]() $U$ that is a refinement of both
$U$ that is a refinement of both ![]() $\mathfrak {S}\cap U$ and
$\mathfrak {S}\cap U$ and ![]() $H\cap U$. By assumption, for any
$H\cap U$. By assumption, for any ![]() $S_\alpha \in \mathfrak {S}$,
$S_\alpha \in \mathfrak {S}$, ![]() $H\cap S_\alpha$ is transverse except at
$H\cap S_\alpha$ is transverse except at ![]() $(0,0)$ in a sufficiently small neighborhood of
$(0,0)$ in a sufficiently small neighborhood of ![]() $(0,0)$. By shrinking
$(0,0)$. By shrinking ![]() $U$ if necessary, we may assume this is always true in
$U$ if necessary, we may assume this is always true in ![]() $U-\{(0,0)\}$. In particular,
$U-\{(0,0)\}$. In particular, ![]() $\mathfrak {S}'$ is a refinement of
$\mathfrak {S}'$ is a refinement of ![]() $\{S_\alpha \cap H\cap (U-\{(0,0)\}), \{(0,0)\}: S_\alpha \in \mathfrak {S}\}$. There exists a continuous function
$\{S_\alpha \cap H\cap (U-\{(0,0)\}), \{(0,0)\}: S_\alpha \in \mathfrak {S}\}$. There exists a continuous function ![]() $\rho : (0,1)\rightarrow \mathbf {R}_+$ with
$\rho : (0,1)\rightarrow \mathbf {R}_+$ with ![]() $\rho (\epsilon )>\epsilon$ and
$\rho (\epsilon )>\epsilon$ and ![]() ${\rho (\epsilon )}/{\epsilon }\rightarrow 1, \epsilon \rightarrow 0^+$, such that
${\rho (\epsilon )}/{\epsilon }\rightarrow 1, \epsilon \rightarrow 0^+$, such that ![]() $\partial B_\delta ((0,\epsilon ))$ is transverse to
$\partial B_\delta ((0,\epsilon ))$ is transverse to ![]() $\mathfrak {S}'$ for all
$\mathfrak {S}'$ for all ![]() $\epsilon <\delta < \rho (\epsilon )$ and
$\epsilon <\delta < \rho (\epsilon )$ and ![]() $0<\epsilon \ll 1$. Then the microlocal stalk of a given sheaf
$0<\epsilon \ll 1$. Then the microlocal stalk of a given sheaf ![]() $\mathcal {G}\in \mathrm {Shv}_{\mathcal {S}}(X)$ at
$\mathcal {G}\in \mathrm {Shv}_{\mathcal {S}}(X)$ at ![]() $(x_0, \xi _0)$, with respect to the local Morse function
$(x_0, \xi _0)$, with respect to the local Morse function ![]() $f$, can be calculated by
$f$, can be calculated by
By assumption, for any ![]() $(x,t)\in \partial B_{\rho (\epsilon )}((0,\epsilon ))\cap \{t=0\}\cap S_\alpha$, where
$(x,t)\in \partial B_{\rho (\epsilon )}((0,\epsilon ))\cap \{t=0\}\cap S_\alpha$, where ![]() $S_\alpha \in \mathfrak {S}$ and
$S_\alpha \in \mathfrak {S}$ and ![]() $0<\epsilon \ll 1$, any nontrivial linear combination of the conormal vectors of
$0<\epsilon \ll 1$, any nontrivial linear combination of the conormal vectors of ![]() $\partial B_{\rho (\epsilon )}((0,\epsilon ))$ and
$\partial B_{\rho (\epsilon )}((0,\epsilon ))$ and ![]() $-dt$ is not in
$-dt$ is not in ![]() $\Lambda _{\mathfrak {S}}$. Hence, we can choose a standard (sufficiently local) smoothing
$\Lambda _{\mathfrak {S}}$. Hence, we can choose a standard (sufficiently local) smoothing ![]() $H_\epsilon$ of the hypersurface
$H_\epsilon$ of the hypersurface ![]() $H_\epsilon ':=(\partial B_{\rho (\epsilon )}((0,\epsilon ))\cap \{t\leq 0\})\cup (H\cap (U- B_{\rho (\epsilon )}((0,\epsilon )))$, so that:
$H_\epsilon ':=(\partial B_{\rho (\epsilon )}((0,\epsilon ))\cap \{t\leq 0\})\cup (H\cap (U- B_{\rho (\epsilon )}((0,\epsilon )))$, so that:
– let
 $f_\epsilon$ be a defining function of
$f_\epsilon$ be a defining function of  $H_\epsilon$, i.e.
$H_\epsilon$, i.e.  $H_\epsilon =\{f_\epsilon =0\}$ and
$H_\epsilon =\{f_\epsilon =0\}$ and  $df_\epsilon |_{H_\epsilon }$ is nowhere
$df_\epsilon |_{H_\epsilon }$ is nowhere  $0$, so that
$0$, so that  $f_\epsilon >0$ for
$f_\epsilon >0$ for  $t>0$; then
$t>0$; then  $df_\epsilon ({-}\partial _t)<0$ along
$df_\epsilon ({-}\partial _t)<0$ along  $H_\epsilon$;
$H_\epsilon$;–
 $df_\epsilon |_{H_\epsilon }\cap \Lambda _\mathfrak {S}=\emptyset$.
$df_\epsilon |_{H_\epsilon }\cap \Lambda _\mathfrak {S}=\emptyset$.
See Figure 3 for an illustration. Let ![]() $H_0=H\cap U$ and
$H_0=H\cap U$ and ![]() $f_0=-t$. Let
$f_0=-t$. Let ![]() $U_\epsilon =\{f_\epsilon >0\}$ for all
$U_\epsilon =\{f_\epsilon >0\}$ for all ![]() $0\leq \epsilon \ll 1$. For
$0\leq \epsilon \ll 1$. For ![]() $\epsilon >0$ sufficiently small, there exists a sufficiently small open cone
$\epsilon >0$ sufficiently small, there exists a sufficiently small open cone ![]() $\Omega$ in
$\Omega$ in ![]() $T^*U$ containing
$T^*U$ containing ![]() $(0,0;0,-dt)$, such that
$(0,0;0,-dt)$, such that ![]() $U_0$ and
$U_0$ and ![]() $U_\epsilon$ can be made as
$U_\epsilon$ can be made as ![]() $H_{a, 0}^{\dagger}$ and
$H_{a, 0}^{\dagger}$ and ![]() $H_{a,\epsilon }^{\dagger}$ for an
$H_{a,\epsilon }^{\dagger}$ for an ![]() $\Omega$-lens, in the sense of [Reference Jin and TreumannJT24, § 2.7.2]. Let
$\Omega$-lens, in the sense of [Reference Jin and TreumannJT24, § 2.7.2]. Let ![]() $\mathcal {F}_{\epsilon,f}:=\mathrm {Cone}(j_{0, !}\mathbf {k}_{U_0}\to j_{\epsilon, !}\mathbf {k}_{U_\epsilon })$. We call these the standard sheaves associated to the
$\mathcal {F}_{\epsilon,f}:=\mathrm {Cone}(j_{0, !}\mathbf {k}_{U_0}\to j_{\epsilon, !}\mathbf {k}_{U_\epsilon })$. We call these the standard sheaves associated to the ![]() $\Omega$-lenses.
$\Omega$-lenses.
Lemma 5.2 There is a canonical isomorphism

Figure 3. An illustration of ![]() $S_0, H=H_0, (x_0,\xi _0)=(0,0;0, -dt)$, the curves
$S_0, H=H_0, (x_0,\xi _0)=(0,0;0, -dt)$, the curves ![]() $\partial B_{\rho (\epsilon )}((0,\epsilon ))$ (the dashed circles), and the smoothings
$\partial B_{\rho (\epsilon )}((0,\epsilon ))$ (the dashed circles), and the smoothings ![]() $H_\epsilon$ (the dashed curves that have tangency with
$H_\epsilon$ (the dashed curves that have tangency with ![]() $H$). The shaded region enclosed by the dashed
$H$). The shaded region enclosed by the dashed ![]() $H_\epsilon$ and the solid
$H_\epsilon$ and the solid ![]() $H_0$ is
$H_0$ is ![]() $U_\epsilon -U_0$.
$U_\epsilon -U_0$.
Proof. The isomorphism comes from a direct application of the non-characteristic deformation lemma (cf. [Reference Kashiwara and SchapiraKS94, Proposition 2.7.2] and [Reference Jin and TreumannJT24, Proposition 2.7.1]). For a fixed ![]() $\delta >0$, we can choose
$\delta >0$, we can choose ![]() $U_{\epsilon }, \epsilon <\delta$, as above satisfying
$U_{\epsilon }, \epsilon <\delta$, as above satisfying ![]() $B_{\rho (\delta )}((0,\delta ))=\bigcup _{\epsilon <\delta }(U_\epsilon \cap B_{\rho (\delta )}((0,\delta )))$. By the assumption that
$B_{\rho (\delta )}((0,\delta ))=\bigcup _{\epsilon <\delta }(U_\epsilon \cap B_{\rho (\delta )}((0,\delta )))$. By the assumption that ![]() $df_\epsilon |_{H_\epsilon }\cap \Lambda _\mathfrak {S}=\emptyset$, the non-characteristic deformation lemma implies that the restriction morphism
$df_\epsilon |_{H_\epsilon }\cap \Lambda _\mathfrak {S}=\emptyset$, the non-characteristic deformation lemma implies that the restriction morphism
is an isomorphism for all ![]() $0<\epsilon <\delta$. Now taking the sections relative to
$0<\epsilon <\delta$. Now taking the sections relative to ![]() $\Gamma (\{t>0\}\cap B_{\rho (\delta )}((0,\delta ));\mathcal {G})$ on both sides, we get exactly (5.2.1).
$\Gamma (\{t>0\}\cap B_{\rho (\delta )}((0,\delta ));\mathcal {G})$ on both sides, we get exactly (5.2.1).
5.2.2 Simplification of sheaves
Lemma 5.2 allows us to calculate microlocal stalks using ![]() $\mathcal {F}_{\epsilon,f}$ satisfying
$\mathcal {F}_{\epsilon,f}$ satisfying ![]() $\mathit {SS}(\mathcal {F}_{\epsilon,f})\cap \mathring {T}^*(U)\subset \Omega$, where
$\mathit {SS}(\mathcal {F}_{\epsilon,f})\cap \mathring {T}^*(U)\subset \Omega$, where ![]() $\Omega$ can be an arbitrarily small conic neighborhood of
$\Omega$ can be an arbitrarily small conic neighborhood of ![]() $(x_0,\xi _0)=(0,0;0,-dt)$. This allows us to use certain localization process (which is the basic idea in [Reference Kashiwara and SchapiraKS94]) to ‘simplify’ any sheaf
$(x_0,\xi _0)=(0,0;0,-dt)$. This allows us to use certain localization process (which is the basic idea in [Reference Kashiwara and SchapiraKS94]) to ‘simplify’ any sheaf ![]() $\mathcal {G}\in \mathrm {Shv}_{\mathcal {S}}(X)$, that has no effect on calculating
$\mathcal {G}\in \mathrm {Shv}_{\mathcal {S}}(X)$, that has no effect on calculating ![]() $\mu _{(x_0, \xi _0;f)}(\mathcal {G})$. To make this work for all choices of local Morse functions, we will assume
$\mu _{(x_0, \xi _0;f)}(\mathcal {G})$. To make this work for all choices of local Morse functions, we will assume ![]() $S_0=\{t=x_{r_0+1}=\cdots =x_r=0\}$ in
$S_0=\{t=x_{r_0+1}=\cdots =x_r=0\}$ in ![]() $U$, where
$U$, where ![]() $r_0=\dim S_0$. Then for different choices of
$r_0=\dim S_0$. Then for different choices of ![]() $f$,
$f$, ![]() $\{f=0\}$ give different hypersurfaces and the sheaves
$\{f=0\}$ give different hypersurfaces and the sheaves ![]() $\mathcal {F}_{\epsilon, f}$ will be depending on
$\mathcal {F}_{\epsilon, f}$ will be depending on ![]() $f$. In the following, without loss of generality (since all calculations are local), we will assume
$f$. In the following, without loss of generality (since all calculations are local), we will assume ![]() $X=\mathbf {R}^r\times \mathbf {R}$ and let
$X=\mathbf {R}^r\times \mathbf {R}$ and let ![]() $S_0'=\{t=x_{r_0+1}=\cdots =x_r=0\}$ (now the picture differs from Figure 3 by a diffeomorphism).
$S_0'=\{t=x_{r_0+1}=\cdots =x_r=0\}$ (now the picture differs from Figure 3 by a diffeomorphism).
For any closed conic subset ![]() $Z\subset T^*X$, write
$Z\subset T^*X$, write ![]() $\mathrm {Shv}_Z(X;\mathbf {k})$ for the full subcategory of
$\mathrm {Shv}_Z(X;\mathbf {k})$ for the full subcategory of ![]() $\mathrm {Shv}(X;\mathbf {k})$ with singular support contained in
$\mathrm {Shv}(X;\mathbf {k})$ with singular support contained in ![]() $Z$. Write
$Z$. Write ![]() $\mathrm {Shv}(X;\mathbf {k})/\mathrm {Shv}_Z(X;\mathbf {k})$ for the right orthogonal complement of
$\mathrm {Shv}(X;\mathbf {k})/\mathrm {Shv}_Z(X;\mathbf {k})$ for the right orthogonal complement of ![]() $\mathrm {Shv}_Z(X;\mathbf {k})$, and for any closed conic subset
$\mathrm {Shv}_Z(X;\mathbf {k})$, and for any closed conic subset ![]() $W$ of
$W$ of ![]() $T^*X-Z$, write
$T^*X-Z$, write ![]() $(\mathrm {Shv}(X;\mathbf {k})/\mathrm {Shv}_Z(X;\mathbf {k}))_W$ for the full subcategory of
$(\mathrm {Shv}(X;\mathbf {k})/\mathrm {Shv}_Z(X;\mathbf {k}))_W$ for the full subcategory of ![]() $\mathrm {Shv}(X;\mathbf {k})/\mathrm {Shv}_Z(X;\mathbf {k})$ whose objects
$\mathrm {Shv}(X;\mathbf {k})/\mathrm {Shv}_Z(X;\mathbf {k})$ whose objects ![]() $\mathcal {F}$ satisfy
$\mathcal {F}$ satisfy ![]() $\mathit {SS}(\mathcal {F})\cap (T^*X-Z)\subset W$. Following Tamarkin, let
$\mathit {SS}(\mathcal {F})\cap (T^*X-Z)\subset W$. Following Tamarkin, let ![]() $\mathrm {Shv}_{\geq 0}(\mathbf {R}^r\times \mathbf {R}_{t};\mathbf {k})$ be the full subcategory of sheaves on
$\mathrm {Shv}_{\geq 0}(\mathbf {R}^r\times \mathbf {R}_{t};\mathbf {k})$ be the full subcategory of sheaves on ![]() $\mathbf {R}^r\times \mathbf {R}_t$, whose singular support is contained in
$\mathbf {R}^r\times \mathbf {R}_t$, whose singular support is contained in ![]() $T^{*, \geq 0}(\mathbf {R}^r\times \mathbf {R}_t)$. Let
$T^{*, \geq 0}(\mathbf {R}^r\times \mathbf {R}_t)$. Let ![]() $\mathrm {Shv}^{<0}(\mathbf {R}^r\times \mathbf {R};\mathbf {k})$ be the left orthogonal complement of
$\mathrm {Shv}^{<0}(\mathbf {R}^r\times \mathbf {R};\mathbf {k})$ be the left orthogonal complement of ![]() $\mathrm {Shv}_{\geq 0}(\mathbf {R}^r\times \mathbf {R};\mathbf {k})$, which is generated by the standard sheaves associated to
$\mathrm {Shv}_{\geq 0}(\mathbf {R}^r\times \mathbf {R};\mathbf {k})$, which is generated by the standard sheaves associated to ![]() $T^{*,<0}(\mathbf {R}^r\times \mathbf {R})$-lenses under small colimits. For any closed conic
$T^{*,<0}(\mathbf {R}^r\times \mathbf {R})$-lenses under small colimits. For any closed conic ![]() $\Lambda \subset T^{*,<0}(\mathbf {R}^r\times \mathbf {R}_t)$, let
$\Lambda \subset T^{*,<0}(\mathbf {R}^r\times \mathbf {R}_t)$, let ![]() $\mathrm {Shv}^{<0}_{\Lambda }(\mathbf {R}^r\times \mathbf {R}_t;\mathbf {k})$ be the full subcategory of
$\mathrm {Shv}^{<0}_{\Lambda }(\mathbf {R}^r\times \mathbf {R}_t;\mathbf {k})$ be the full subcategory of ![]() $\mathrm {Shv}^{<0}(\mathbf {R}^r\times \mathbf {R}_{t};\mathbf {k})$ consisting of
$\mathrm {Shv}^{<0}(\mathbf {R}^r\times \mathbf {R}_{t};\mathbf {k})$ consisting of ![]() $\mathcal {F}$ with
$\mathcal {F}$ with ![]() $\mathit {SS}(\mathcal {F})\cap T^{*,<0}(\mathbf {R}^r\times \mathbf {R}_t)\subset \Lambda$. Let
$\mathit {SS}(\mathcal {F})\cap T^{*,<0}(\mathbf {R}^r\times \mathbf {R}_t)\subset \Lambda$. Let ![]() $\Lambda _{S'_0}^{<0}=T^{*}_{S'_0}(\mathbf {R}^r\times \mathbf {R})\cap T^{*,<0}(\mathbf {R}^r\times \mathbf {R}_t)$.
$\Lambda _{S'_0}^{<0}=T^{*}_{S'_0}(\mathbf {R}^r\times \mathbf {R})\cap T^{*,<0}(\mathbf {R}^r\times \mathbf {R}_t)$.
Lemma 5.3 For any sheaf ![]() $\mathcal {G}\in \mathrm {Shv}_{\mathcal {S}}(\mathbf {R}^r\times \mathbf {R};\mathbf {k})$, there exists a sheaf
$\mathcal {G}\in \mathrm {Shv}_{\mathcal {S}}(\mathbf {R}^r\times \mathbf {R};\mathbf {k})$, there exists a sheaf ![]() $\mathcal {G}'\in \mathrm {Shv}_{\Lambda _{S'_0}^{<0}}^{<0}(\mathbf {R}^r\times \mathbf {R}_t;\mathbf {k})$ (unique up to isomorphisms) with a zig-zag of morphisms
$\mathcal {G}'\in \mathrm {Shv}_{\Lambda _{S'_0}^{<0}}^{<0}(\mathbf {R}^r\times \mathbf {R}_t;\mathbf {k})$ (unique up to isomorphisms) with a zig-zag of morphisms ![]() $\mathcal {G}\to \mathcal {M}\leftarrow \mathcal {G}'$ in
$\mathcal {G}\to \mathcal {M}\leftarrow \mathcal {G}'$ in ![]() $\mathrm {Shv}(\mathbf {R}^r\times \mathbf {R};\mathbf {k})$, such that for any local Morse function
$\mathrm {Shv}(\mathbf {R}^r\times \mathbf {R};\mathbf {k})$, such that for any local Morse function ![]() $f$ as above, the zig-zag of morphisms induces isomorphisms
$f$ as above, the zig-zag of morphisms induces isomorphisms
for all ![]() $\epsilon >0$ sufficiently small.
$\epsilon >0$ sufficiently small.
Proof. Note that the natural functor
(cf. [Reference Jin and TreumannJT24, § 2.8.2] for the notation ![]() $\text {MSh}^{\text {p}}_Z$; for a more thorough discussion about
$\text {MSh}^{\text {p}}_Z$; for a more thorough discussion about ![]() $\text {MSh}^{\text {p}}_Z$, we refer the reader to [Reference Kashiwara and SchapiraKS94] and [Reference Nadler and ShendeNS20, Section 6]) is an equivalence. There exists a decreasing sequence of open conic neighborhoods
$\text {MSh}^{\text {p}}_Z$, we refer the reader to [Reference Kashiwara and SchapiraKS94] and [Reference Nadler and ShendeNS20, Section 6]) is an equivalence. There exists a decreasing sequence of open conic neighborhoods ![]() $\{\Omega _n\}_{n\geq 0}$ of
$\{\Omega _n\}_{n\geq 0}$ of ![]() $(x_0,\xi _0)$ whose intersection is
$(x_0,\xi _0)$ whose intersection is ![]() $\mathbf {R}_+\cdot (x_0, \xi _0)$ such that
$\mathbf {R}_+\cdot (x_0, \xi _0)$ such that
is an equivalence for all ![]() $n$. For any
$n$. For any ![]() $n$ sufficiently large, set the
$n$ sufficiently large, set the ![]() $\Omega$ in § 5.2.1 to be
$\Omega$ in § 5.2.1 to be ![]() $\Omega _n$. Let
$\Omega _n$. Let ![]() $\mathcal {M}$ be the image of
$\mathcal {M}$ be the image of ![]() $\mathcal {G}$ under the localization functor
$\mathcal {G}$ under the localization functor
so then ![]() $\mathcal {M}$ lands in the left-hand side of (5.2.4). Since (5.2.3) factors through (5.2.4), there is
$\mathcal {M}$ lands in the left-hand side of (5.2.4). Since (5.2.3) factors through (5.2.4), there is ![]() $\mathcal {G}'\in \mathrm {Shv}^{<0}_{\Lambda _{S'_0}^{<0}}(\mathbf {R}^r\times \mathbf {R}_t;\mathbf {k})$ (unique up to isomorphisms) whose image in the left-hand side of (5.2.4) is isomorphic to
$\mathcal {G}'\in \mathrm {Shv}^{<0}_{\Lambda _{S'_0}^{<0}}(\mathbf {R}^r\times \mathbf {R}_t;\mathbf {k})$ (unique up to isomorphisms) whose image in the left-hand side of (5.2.4) is isomorphic to ![]() $\mathcal {M}$. Thus, we have a zig-zag of morphisms
$\mathcal {M}$. Thus, we have a zig-zag of morphisms ![]() $\mathcal {G}\to \mathcal {M}\leftarrow \mathcal {G}'$. Since the fiber of each map has singular support outside of
$\mathcal {G}\to \mathcal {M}\leftarrow \mathcal {G}'$. Since the fiber of each map has singular support outside of ![]() $\Omega$ (so they are right orthogonal to any standard sheaf associated to an
$\Omega$ (so they are right orthogonal to any standard sheaf associated to an ![]() $\Omega$-lens [Reference Jin and TreumannJT24, § 2.7.2]), for all
$\Omega$-lens [Reference Jin and TreumannJT24, § 2.7.2]), for all ![]() $\epsilon$ sufficiently small, we get the isomorphisms (5.2.2) by taking
$\epsilon$ sufficiently small, we get the isomorphisms (5.2.2) by taking ![]() $\mathrm {Hom}(\mathcal {F}_{\epsilon, f}, -)$.
$\mathrm {Hom}(\mathcal {F}_{\epsilon, f}, -)$.
Remark 5.4 Using the equivalences (5.2.4), we get a well-defined equivalence

Using this equivalence for (the non-canonical) ![]() $\simeq$ in (5.2.3), the composition is identified with
$\simeq$ in (5.2.3), the composition is identified with ![]() $\mathrm {Hom}(\mathcal {F}_{\epsilon,f}\text {, })$ for any
$\mathrm {Hom}(\mathcal {F}_{\epsilon,f}\text {, })$ for any ![]() $\epsilon >0$ sufficiently small. The same holds when
$\epsilon >0$ sufficiently small. The same holds when ![]() $\mathrm {Shv}^{<0}_{\Lambda _{S'_0}^{<0}}(\mathbf {R}^r\times \mathbf {R}_t;\mathbf {k})$ is replaced by
$\mathrm {Shv}^{<0}_{\Lambda _{S'_0}^{<0}}(\mathbf {R}^r\times \mathbf {R}_t;\mathbf {k})$ is replaced by ![]() $\mathrm {Shv}_{\mathfrak {S}}(\mathbf {R}^r\times \mathbf {R}_t;\mathbf {k})$.
$\mathrm {Shv}_{\mathfrak {S}}(\mathbf {R}^r\times \mathbf {R}_t;\mathbf {k})$.
5.2.3 Quantized (stabilized) Morse transformations as (stabilized) Morse kernels
We will see soon that the correspondence given by a Morse transformation is exactly calculating the microlocal stalks ![]() $\mu _{(x_0,\xi _0;f)}$, for the local Morse function
$\mu _{(x_0,\xi _0;f)}$, for the local Morse function ![]() $f$ given by
$f$ given by ![]() $-t_0+p_0\cdot \mathbf {q}_0+\frac {1}{2}A_S(\mathbf {q})$ in Proposition 5.1(a) (up to adding a factor that forms a convex space). This is established in Corollary 5.6 below.
$-t_0+p_0\cdot \mathbf {q}_0+\frac {1}{2}A_S(\mathbf {q})$ in Proposition 5.1(a) (up to adding a factor that forms a convex space). This is established in Corollary 5.6 below.
Both Morse transformations and stratified Morse functions can be stabilized in the following way. Using the notation from Proposition 5.1, we stabilize a (germ of a) Lagrangian ![]() $L\subset T^*\mathbf {R}^{M}$ by taking
$L\subset T^*\mathbf {R}^{M}$ by taking ![]() $L\times T^*_{\mathbf {R}}\mathbf {R}_{y_1}\times T^*_{\mathbf {R}}\mathbf {R}_{y_2}\times \cdots$ in
$L\times T^*_{\mathbf {R}}\mathbf {R}_{y_1}\times T^*_{\mathbf {R}}\mathbf {R}_{y_2}\times \cdots$ in ![]() $T^*\mathbf {R}^M\times T^*\mathbf {R}_{y_1}\times T^*\mathbf {R}_{y_1}\times \cdots$. Then we stabilize the Morse transformation given in (5.1.1), by adding
$T^*\mathbf {R}^M\times T^*\mathbf {R}_{y_1}\times T^*\mathbf {R}_{y_1}\times \cdots$. Then we stabilize the Morse transformation given in (5.1.1), by adding ![]() $-(y_1^2+y_2^2+\cdots )$ to
$-(y_1^2+y_2^2+\cdots )$ to ![]() $A_S$. For a stratification
$A_S$. For a stratification ![]() $\mathfrak {S}=\{S_\alpha \}$, we stabilize it in the usual way:
$\mathfrak {S}=\{S_\alpha \}$, we stabilize it in the usual way: ![]() $\{S_\alpha \times \mathbf {R}_{y_1}\times \mathbf {R}_{y_2}\cdots \}$. For a local Morse function
$\{S_\alpha \times \mathbf {R}_{y_1}\times \mathbf {R}_{y_2}\cdots \}$. For a local Morse function ![]() $f$ as in § 5.2.1, we stabilize
$f$ as in § 5.2.1, we stabilize ![]() $f$ by adding
$f$ by adding ![]() $-\frac {1}{2}(y_1^2+y_2^2+\cdots )$.
$-\frac {1}{2}(y_1^2+y_2^2+\cdots )$.
5.3 The relevant localization of sheaf categories
For a germ of a smooth conic Lagrangian ![]() $(\mathbf {L}, (x_0,\xi _0)=(0,p_0;t_0=0,-dt_0))$ in
$(\mathbf {L}, (x_0,\xi _0)=(0,p_0;t_0=0,-dt_0))$ in ![]() $T^{*,<0}(\mathbf {R}^M\times \mathbf {R}_{t_0})$ as above, we can choose a diffeomorphism between a sufficiently small ball containing the front projection of
$T^{*,<0}(\mathbf {R}^M\times \mathbf {R}_{t_0})$ as above, we can choose a diffeomorphism between a sufficiently small ball containing the front projection of ![]() $\mathbf {L}$ with
$\mathbf {L}$ with ![]() $\mathbf {R}^M\times \mathbf {R}_{t_0}$ which is the identity near the origin and sends negative covectors to negative covectors, so then the germ of front is sent to a closed front in
$\mathbf {R}^M\times \mathbf {R}_{t_0}$ which is the identity near the origin and sends negative covectors to negative covectors, so then the germ of front is sent to a closed front in ![]() $\mathbf {R}^M\times \mathbf {R}_{t_0}$. Let
$\mathbf {R}^M\times \mathbf {R}_{t_0}$. Let ![]() $\widetilde {\mathbf {L}}$ be the conic Lagrangian determined by the resulting front. For any interval
$\widetilde {\mathbf {L}}$ be the conic Lagrangian determined by the resulting front. For any interval ![]() $I\subset (-\infty,\infty )$, we have a correspondence
$I\subset (-\infty,\infty )$, we have a correspondence

where ![]() $\pi _{12}$ is the projection to the first two factors and
$\pi _{12}$ is the projection to the first two factors and ![]() $m_I$ is the addition operation
$m_I$ is the addition operation ![]() $\mathbf {R}_t\times I\rightarrow \mathbf {R}_t$ and projection in
$\mathbf {R}_t\times I\rightarrow \mathbf {R}_t$ and projection in ![]() $\mathbf {R}^M$. We define the convolution functor
$\mathbf {R}^M$. We define the convolution functor ![]() $T_I$ to be
$T_I$ to be
The convolution functor ![]() $T_{(-\infty,0]}$ defines a localization functor which corresponds to the localizing subcategory
$T_{(-\infty,0]}$ defines a localization functor which corresponds to the localizing subcategory ![]() $\mathrm {Shv}_{\geq 0}(\mathbf {R}^M\times \mathbf {R}_{t_0};\mathrm {Sp})$, whose essential image is
$\mathrm {Shv}_{\geq 0}(\mathbf {R}^M\times \mathbf {R}_{t_0};\mathrm {Sp})$, whose essential image is ![]() $\mathrm {Shv}^{<0}(\mathbf {R}^M\times \mathbf {R}_{t_0};\mathrm {Sp})$ (cf. [Reference TamarkinTam15, Reference Jin and TreumannJT24]). The above produces (canonically) equivalent localized sheaf categories
$\mathrm {Shv}^{<0}(\mathbf {R}^M\times \mathbf {R}_{t_0};\mathrm {Sp})$ (cf. [Reference TamarkinTam15, Reference Jin and TreumannJT24]). The above produces (canonically) equivalent localized sheaf categories
regardless of the choice of the diffeomorphism. Hence, we will abuse notation and use ![]() $\mathrm {Shv}_{\mathbf {L}}^0(\mathbf {R}^M\times \mathbf {R}_{t_0};\mathrm {Sp})$ to denote the localized category in (5.3.1) without reference to any particular choice of
$\mathrm {Shv}_{\mathbf {L}}^0(\mathbf {R}^M\times \mathbf {R}_{t_0};\mathrm {Sp})$ to denote the localized category in (5.3.1) without reference to any particular choice of ![]() $\widetilde {\mathbf {L}}$. We note that
$\widetilde {\mathbf {L}}$. We note that ![]() $\mathrm {Shv}_{\mathbf {L}}^0(\mathbf {R}^M\times \mathbf {R}_{t_0};\mathrm {Sp})$ is naturally equivalent to
$\mathrm {Shv}_{\mathbf {L}}^0(\mathbf {R}^M\times \mathbf {R}_{t_0};\mathrm {Sp})$ is naturally equivalent to ![]() $(\text {MSh}_{\mathbf {L}}^{\text {p}})_{(x_0, \xi _0)}$. In the following, we reserve the notation
$(\text {MSh}_{\mathbf {L}}^{\text {p}})_{(x_0, \xi _0)}$. In the following, we reserve the notation ![]() $\mathrm {Shv}_{\widetilde {\mathbf {L}}}^{<0}(\mathbf {R}^r\times \mathbf {R}_t;\mathbf {k})$ for the left orthogonal complement of
$\mathrm {Shv}_{\widetilde {\mathbf {L}}}^{<0}(\mathbf {R}^r\times \mathbf {R}_t;\mathbf {k})$ for the left orthogonal complement of ![]() $\mathrm {Shv}_{\geq 0}(\mathbf {R}^M\times \mathbf {R}_{t_0};\mathrm {Sp})$ in
$\mathrm {Shv}_{\geq 0}(\mathbf {R}^M\times \mathbf {R}_{t_0};\mathrm {Sp})$ in ![]() $\mathrm {Shv}_{\widetilde {\mathbf {L}}\cup T^{*,\geq 0}(\mathbf {R}^M\times \mathbf {R}_{t_0})}(\mathbf {R}^M\times \mathbf {R}_{t_0};\mathrm {Sp})$.
$\mathrm {Shv}_{\widetilde {\mathbf {L}}\cup T^{*,\geq 0}(\mathbf {R}^M\times \mathbf {R}_{t_0})}(\mathbf {R}^M\times \mathbf {R}_{t_0};\mathrm {Sp})$.
Given any Morse transformation ![]() $\mathbf {L}_{01}$ sending
$\mathbf {L}_{01}$ sending ![]() $(\mathbf {L}, (0,p_0;t_0=0,-dt_0))$ to
$(\mathbf {L}, (0,p_0;t_0=0,-dt_0))$ to ![]() $(\mathbf {L}_1, (0,p_1;t_1=0,-dt_1))$, it determines a correspondence (where
$(\mathbf {L}_1, (0,p_1;t_1=0,-dt_1))$, it determines a correspondence (where ![]() $\pi (\mathbf {L}_{01})$ can be globalized to a smooth hypersurface)
$\pi (\mathbf {L}_{01})$ can be globalized to a smooth hypersurface)

that induces an equivalence of localized sheaf categories
Since, by assumption, ![]() $\mathbf {L}_1$ is the negative conormal bundle of a germ of a smooth hypersurface defined by
$\mathbf {L}_1$ is the negative conormal bundle of a germ of a smooth hypersurface defined by ![]() $f(\mathbf {q}_1,t_1)=0$, the latter category is equivalent to
$f(\mathbf {q}_1,t_1)=0$, the latter category is equivalent to
for any ![]() $K\gg 1$. Here the added
$K\gg 1$. Here the added ![]() $\Sigma$ is to make Lemma 5.5 and Corollary 5.6 below true without any shift by
$\Sigma$ is to make Lemma 5.5 and Corollary 5.6 below true without any shift by ![]() $\Sigma$. For a more detailed discussion of the equivalences induced by Morse transformations for microlocal sheaves of spectra, we refer the reader to [Reference Jin and TreumannJT24, Section 2.10] and [Reference Nadler and ShendeNS20, Section 6].
$\Sigma$. For a more detailed discussion of the equivalences induced by Morse transformations for microlocal sheaves of spectra, we refer the reader to [Reference Jin and TreumannJT24, Section 2.10] and [Reference Nadler and ShendeNS20, Section 6].
5.3.1 An example when  $\mathbf {L}=\Lambda _{S_0'}^{<0}$
$\mathbf {L}=\Lambda _{S_0'}^{<0}$
Assume we are in the setting of § 5.2.2. Let ![]() $\mathbf {L}=\Lambda _{S_0'}^{<0}$, and write
$\mathbf {L}=\Lambda _{S_0'}^{<0}$, and write ![]() $S_0'=S_{0,\mathbf {q}}'\times \{t_0=0\}\subset \mathbf {R}^M_\mathbf {q}\times \mathbf {R}_{t_0}$. Then there is a natural equivalence
$S_0'=S_{0,\mathbf {q}}'\times \{t_0=0\}\subset \mathbf {R}^M_\mathbf {q}\times \mathbf {R}_{t_0}$. Then there is a natural equivalence
 \begin{align*} \mathrm{Sp}&\overset{\sim}{\to} \mathrm{Shv}_{\mathbf{L}}^{<0}(\mathbf{R}^M\times \mathbf{R}_{t_0};\mathrm{Sp})\simeq \mathrm{Shv}_{\mathbf{L}}^0(\mathbf{R}^M\times\mathbf{R}_{t_0};\mathrm{Sp})\\ \mathcal{M}&\mapsto i_*\mathcal{M}_{S_{0,\mathbf{q}}'\times (-\infty, 0)}, \end{align*}
\begin{align*} \mathrm{Sp}&\overset{\sim}{\to} \mathrm{Shv}_{\mathbf{L}}^{<0}(\mathbf{R}^M\times \mathbf{R}_{t_0};\mathrm{Sp})\simeq \mathrm{Shv}_{\mathbf{L}}^0(\mathbf{R}^M\times\mathbf{R}_{t_0};\mathrm{Sp})\\ \mathcal{M}&\mapsto i_*\mathcal{M}_{S_{0,\mathbf{q}}'\times (-\infty, 0)}, \end{align*}
where ![]() $i: S_{0,\mathbf {q}}'\times (-\infty, 0)\hookrightarrow \mathbf {R}^M\times \mathbf {R}_{t_0}$ is the inclusion. Let
$i: S_{0,\mathbf {q}}'\times (-\infty, 0)\hookrightarrow \mathbf {R}^M\times \mathbf {R}_{t_0}$ is the inclusion. Let ![]() $\mathbf {L}_{01}$ be the Morse transformation defined by (5.1.1), with
$\mathbf {L}_{01}$ be the Morse transformation defined by (5.1.1), with ![]() $p_0=p_1=0$ and
$p_0=p_1=0$ and ![]() $A_S$ a non-degenerate quadratic form on
$A_S$ a non-degenerate quadratic form on ![]() $\pi _*T_{(0,0;0,-dt)}\mathbf {L}=S_0'$ (the identification is through the obvious way).
$\pi _*T_{(0,0;0,-dt)}\mathbf {L}=S_0'$ (the identification is through the obvious way).
Lemma 5.5 Let ![]() $\mathbf {L}=\Lambda _{S_0'}^{<0}$. Then the equivalence (5.3.3), composed with the natural equivalence
$\mathbf {L}=\Lambda _{S_0'}^{<0}$. Then the equivalence (5.3.3), composed with the natural equivalence ![]() $\Upsilon : \mathrm {Shv}_{\mathbf {L}_1}^0(\mathbf {R}^M\times \mathbf {R}_{t_1};\mathrm {Sp})\overset {\sim }{\to } \mathrm {Sp}$ (5.3.4), is explicitly given by
$\Upsilon : \mathrm {Shv}_{\mathbf {L}_1}^0(\mathbf {R}^M\times \mathbf {R}_{t_1};\mathrm {Sp})\overset {\sim }{\to } \mathrm {Sp}$ (5.3.4), is explicitly given by

Proof. First, the correspondence (5.3.2) induces an equivalence
where ![]() $\mathbf {L}_1$ is the negative conormal bundle of a global smooth hypersurface (not just a germ). Indeed, let
$\mathbf {L}_1$ is the negative conormal bundle of a global smooth hypersurface (not just a germ). Indeed, let ![]() $L$ be the conormal bundle of
$L$ be the conormal bundle of ![]() $S'_{0,\mathbf {q}}$ in
$S'_{0,\mathbf {q}}$ in ![]() $T^*\mathbf {R}^M$, then using Proposition 5.1(c), we know that
$T^*\mathbf {R}^M$, then using Proposition 5.1(c), we know that ![]() $\mathbf {L}_1$ is the cone over a Legendrian lifting of the linear Lagrangian graph in
$\mathbf {L}_1$ is the cone over a Legendrian lifting of the linear Lagrangian graph in ![]() $T^*\mathbf {R}^M$, which comes from first doing a Fourier transform of
$T^*\mathbf {R}^M$, which comes from first doing a Fourier transform of ![]() $T^*\mathbf {R}^M$ on
$T^*\mathbf {R}^M$ on ![]() $L$ and then doing
$L$ and then doing ![]() $\varphi _{\frac {1}{2}A_S(\mathbf {p})}^1$. Let
$\varphi _{\frac {1}{2}A_S(\mathbf {p})}^1$. Let ![]() $H\subset \mathbf {R}^M\times \mathbf {R}_{t_1}$ be the projection of
$H\subset \mathbf {R}^M\times \mathbf {R}_{t_1}$ be the projection of ![]() $\mathbf {L}_1$, and let
$\mathbf {L}_1$, and let ![]() $U_-$ be the open subset below
$U_-$ be the open subset below ![]() $H$ (with respect to the orientation from
$H$ (with respect to the orientation from ![]() $\mathbf {R}_{t_1}$). Then we have the obvious equivalence
$\mathbf {R}_{t_1}$). Then we have the obvious equivalence
 \begin{align*} \mathrm{Sp}&\to \mathrm{Shv}_{\mathbf{L}_1}^{<0}(\mathbf{R}^M\times\mathbf{R}_{t_1};\mathrm{Sp})\\ \mathcal{N}&\mapsto j_{U_-,*}\mathcal{N}_{U_-}. \end{align*}
\begin{align*} \mathrm{Sp}&\to \mathrm{Shv}_{\mathbf{L}_1}^{<0}(\mathbf{R}^M\times\mathbf{R}_{t_1};\mathrm{Sp})\\ \mathcal{N}&\mapsto j_{U_-,*}\mathcal{N}_{U_-}. \end{align*}
Let ![]() $\mathfrak {i}_{\mathbf {R}_{t_1}}: \{0\}\times \mathbf {R}_{t_1}\hookrightarrow \mathbf {R}^M\times \mathbf {R}_{t_1}$ (respectively,
$\mathfrak {i}_{\mathbf {R}_{t_1}}: \{0\}\times \mathbf {R}_{t_1}\hookrightarrow \mathbf {R}^M\times \mathbf {R}_{t_1}$ (respectively, ![]() $\mathfrak {i}_{\mathbf {R}_{t_1}^+}: \{0\}\times \mathbf {R}_{t_1}^+\hookrightarrow \mathbf {R}^M\times \mathbf {R}_{t_1}$) be the inclusion. Given
$\mathfrak {i}_{\mathbf {R}_{t_1}^+}: \{0\}\times \mathbf {R}_{t_1}^+\hookrightarrow \mathbf {R}^M\times \mathbf {R}_{t_1}$) be the inclusion. Given ![]() $\mathcal {G}'=i_*\mathcal {M}_{S_{0,\mathbf {q}}'\times (-\infty, 0)}\in \mathrm {Shv}_{\mathbf {L}}^{<0}(\mathbf {R}^M\times \mathbf {R}_{t_0};\mathrm {Sp})$, to see
$\mathcal {G}'=i_*\mathcal {M}_{S_{0,\mathbf {q}}'\times (-\infty, 0)}\in \mathrm {Shv}_{\mathbf {L}}^{<0}(\mathbf {R}^M\times \mathbf {R}_{t_0};\mathrm {Sp})$, to see ![]() $\Psi _{\mathbf {L}_{01}}(\mathcal {G}')|_{U_-}$, it suffices to calculate the fiber of
$\Psi _{\mathbf {L}_{01}}(\mathcal {G}')|_{U_-}$, it suffices to calculate the fiber of
By base change, the left-hand side can be directly identified with ![]() $\Gamma (\mathbf {R}^M\times \mathbf {R}_{t_0}, \mathcal {G}')\cong \mathcal {M}$, and the right-hand side can be directly identified with
$\Gamma (\mathbf {R}^M\times \mathbf {R}_{t_0}, \mathcal {G}')\cong \mathcal {M}$, and the right-hand side can be directly identified with
Thus, the fiber is canonically identified with ![]() $\mu _{(x_0,\xi _0;-t_0+\frac {1}{2}A_S(\mathbf {q}))}(\mathcal {G}')$ as desired.
$\mu _{(x_0,\xi _0;-t_0+\frac {1}{2}A_S(\mathbf {q}))}(\mathcal {G}')$ as desired.
Corollary 5.6 Let ![]() $(\mathbf {L}, (x_0,\xi _0)=(0,0;t_0=0,-dt_0))$ be the germ of a conic open neighborhood of
$(\mathbf {L}, (x_0,\xi _0)=(0,0;t_0=0,-dt_0))$ be the germ of a conic open neighborhood of ![]() $(x_0,\xi _0)\in \Lambda _\mathfrak {S}^{\rm sm}$. Then for any Morse transformation
$(x_0,\xi _0)\in \Lambda _\mathfrak {S}^{\rm sm}$. Then for any Morse transformation ![]() $\mathbf {L}_{01}$ defined by (5.1.1), we have a natural commutative diagram
$\mathbf {L}_{01}$ defined by (5.1.1), we have a natural commutative diagram

where ![]() $\mu$ is the microlocalization functor,
$\mu$ is the microlocalization functor, ![]() $f=-t_0+\frac {1}{2}A_S(\mathbf {q})$ and
$f=-t_0+\frac {1}{2}A_S(\mathbf {q})$ and ![]() $\varinjlim _{\epsilon \to 0^+}\mathrm {Hom}(\mathcal {F}_{\epsilon,f}\text {, })$ is as in Remark 5.4.
$\varinjlim _{\epsilon \to 0^+}\mathrm {Hom}(\mathcal {F}_{\epsilon,f}\text {, })$ is as in Remark 5.4.
It is clear that one can enlarge the space of ![]() $f$ occurring in Corollary 5.6 to the space of
$f$ occurring in Corollary 5.6 to the space of ![]() $f$ whose graph of differential has tangent space at
$f$ whose graph of differential has tangent space at ![]() $(x_0, \xi _0)$ transverse to
$(x_0, \xi _0)$ transverse to ![]() $T_{(x_0,\xi _0)}\mathbf {L}$, which yields a homotopy equivalent space of (local) functions.
$T_{(x_0,\xi _0)}\mathbf {L}$, which yields a homotopy equivalent space of (local) functions.
Remark 5.7 (i) Corollary 5.6 establishes the desired bridge between the effect of Morse transformations and stratified Morse functions on quasi-constructible sheaves (i.e. sheaves that are in ![]() $\mathrm {Shv}_{\mathfrak {S}}(X;\mathrm {Sp})$ for some
$\mathrm {Shv}_{\mathfrak {S}}(X;\mathrm {Sp})$ for some ![]() $\mathfrak {S}$), which is clearly compatible with stabilizations.
$\mathfrak {S}$), which is clearly compatible with stabilizations.
(ii) When ![]() $(x,p)\not \in \Lambda _{\mathfrak {S}}^{\rm sm}$, to calculate the correct microlocal stalk, the conditions on the local Morse functions are not sufficient. If
$(x,p)\not \in \Lambda _{\mathfrak {S}}^{\rm sm}$, to calculate the correct microlocal stalk, the conditions on the local Morse functions are not sufficient. If ![]() $(x,p)\in \Lambda ^{\rm sm}$ for some conic Lagrangian
$(x,p)\in \Lambda ^{\rm sm}$ for some conic Lagrangian ![]() $\Lambda$ (e.g.
$\Lambda$ (e.g. ![]() $(x,p)\in \mathit {SS}(\mathcal {F})^{\rm sm}$ for some
$(x,p)\in \mathit {SS}(\mathcal {F})^{\rm sm}$ for some ![]() $\mathcal {F}\in \mathrm {Shv}_\mathfrak {S}(X;\mathrm {Sp})$), then the condition on a ‘local Morse function’
$\mathcal {F}\in \mathrm {Shv}_\mathfrak {S}(X;\mathrm {Sp})$), then the condition on a ‘local Morse function’ ![]() $f$ is that
$f$ is that ![]() $f(x)=0$ and
$f(x)=0$ and ![]() $\text {Graph}(df)$ intersects
$\text {Graph}(df)$ intersects ![]() $\Lambda ^{\rm sm}$ transversely at
$\Lambda ^{\rm sm}$ transversely at ![]() $(x,p)$. It is easy to see (using the proof of Proposition 5.1(a)) that the space of such
$(x,p)$. It is easy to see (using the proof of Proposition 5.1(a)) that the space of such ![]() $f$ is homotopy equivalent to the space of Morse transformations with respect to
$f$ is homotopy equivalent to the space of Morse transformations with respect to ![]() $(\Lambda ^{\rm sm}, (x, p))$ in the obvious way. With a little more work, one gets a direct generalization of Corollary 5.6 in this setting, without the involvement of
$(\Lambda ^{\rm sm}, (x, p))$ in the obvious way. With a little more work, one gets a direct generalization of Corollary 5.6 in this setting, without the involvement of ![]() $\mathrm {Shv}_{\mathfrak {S}}(\mathbf {R}^M\times \mathbf {R}_{t_0};\mathrm {Sp})$.
$\mathrm {Shv}_{\mathfrak {S}}(\mathbf {R}^M\times \mathbf {R}_{t_0};\mathrm {Sp})$.
5.3.2 A reformulation of Proposition 4.11
If we drop the condition ![]() $s<-\frac {1}{2}|\mathbf {q}|^2+A(\mathbf {q})$ in (4.1.1), then we can view
$s<-\frac {1}{2}|\mathbf {q}|^2+A(\mathbf {q})$ in (4.1.1), then we can view ![]() $G_N\times \mathbf {R}^M\times \mathbf {R}_s$ as the underlying space of a
$G_N\times \mathbf {R}^M\times \mathbf {R}_s$ as the underlying space of a ![]() $VG_N^\bullet$-module in
$VG_N^\bullet$-module in ![]() $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$, and we have a natural morphism of
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$, and we have a natural morphism of ![]() $VG_N^\bullet$-modules
$VG_N^\bullet$-modules
Let ![]() $\mathbf {L}_{\widehat {Q}_{N,M}}$ be the negative conormal of the boundary of
$\mathbf {L}_{\widehat {Q}_{N,M}}$ be the negative conormal of the boundary of ![]() $\widehat {Q}_{N,M}$ in
$\widehat {Q}_{N,M}$ in ![]() $G_N\times \mathbf {R}^M\times \mathbf {R}_s$. Then
$G_N\times \mathbf {R}^M\times \mathbf {R}_s$. Then ![]() $\mathrm {Shv}^0_{\mathbf {L}_{\widehat {Q}_{N,M}}}(G_N\times \mathbf {R}^M\times \mathbf {R}_s;\mathrm {Sp})$ is equivalent to the essential image of
$\mathrm {Shv}^0_{\mathbf {L}_{\widehat {Q}_{N,M}}}(G_N\times \mathbf {R}^M\times \mathbf {R}_s;\mathrm {Sp})$ is equivalent to the essential image of ![]() $(\iota _{N,M})_*$. Since
$(\iota _{N,M})_*$. Since ![]() $\iota _{N,M}$ is open and for any
$\iota _{N,M}$ is open and for any ![]() $(N',M')\geq (N,M)$ the diagram
$(N',M')\geq (N,M)$ the diagram

is Cartesian, a direct application of Proposition 2.28 gives an isomorphism
 \begin{align*}
&\varprojlim_{N,M}(\iota_{N,M})_*:\\
&(\mathrm{Loc}(VG;\mathrm{Sp})^{\otimes_c},
\mathrm{Loc}(\widehat{Q};\mathrm{Sp}))\overset{\sim}{\rightarrow}
\Bigl (\mathrm{Loc}(VG;\mathrm{Sp})^{\otimes_c},
\varprojlim_{N,M}\mathrm{Shv}^0_{\mathbf{L}_{\widehat{Q}_{N,M}}}(G_N\times
\mathbf{R}^M\times \mathbf{R}_s;\mathrm{Sp}) \Bigr)
\end{align*}
\begin{align*}
&\varprojlim_{N,M}(\iota_{N,M})_*:\\
&(\mathrm{Loc}(VG;\mathrm{Sp})^{\otimes_c},
\mathrm{Loc}(\widehat{Q};\mathrm{Sp}))\overset{\sim}{\rightarrow}
\Bigl (\mathrm{Loc}(VG;\mathrm{Sp})^{\otimes_c},
\varprojlim_{N,M}\mathrm{Shv}^0_{\mathbf{L}_{\widehat{Q}_{N,M}}}(G_N\times
\mathbf{R}^M\times \mathbf{R}_s;\mathrm{Sp}) \Bigr)
\end{align*}
in ![]() $\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$. Similarly, let
$\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$. Similarly, let ![]() $\mathbf {L}_{Q_M^0}$ denote the negative conormal of the boundary of
$\mathbf {L}_{Q_M^0}$ denote the negative conormal of the boundary of ![]() $Q_0^M$. Then we have a canonical equivalence
$Q_0^M$. Then we have a canonical equivalence
Now we can rewrite Proposition 4.11 in the following form.
Corollary 5.8 There is a natural isomorphism in ![]() $\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$
$\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$
 \begin{align} & F_{Q^0}\circ p^*: \Bigl (\mathrm{Loc}(G;\mathrm{Sp})^{\otimes_c}, \varprojlim_{N,M} \mathrm{Shv}_{\mathbf{L}_{\widehat{Q}_{N,M}}}^0(G_N\times \mathbf{R}^M\times \mathbf{R}_s;\mathrm{Sp}) \Bigr)\nonumber\\ &\quad \overset{\sim}{\rightarrow} \Bigl (\mathrm{Loc}(VG;\mathrm{Sp})^{\otimes_c}, \varprojlim_{N,M} \mathrm{Shv}_{\mathbf{L}_{\widehat{Q}_{N,M}}}^0(G_N\times \mathbf{R}^M\times \mathbf{R}_s;\mathrm{Sp})\Bigr) \end{align}
\begin{align} & F_{Q^0}\circ p^*: \Bigl (\mathrm{Loc}(G;\mathrm{Sp})^{\otimes_c}, \varprojlim_{N,M} \mathrm{Shv}_{\mathbf{L}_{\widehat{Q}_{N,M}}}^0(G_N\times \mathbf{R}^M\times \mathbf{R}_s;\mathrm{Sp}) \Bigr)\nonumber\\ &\quad \overset{\sim}{\rightarrow} \Bigl (\mathrm{Loc}(VG;\mathrm{Sp})^{\otimes_c}, \varprojlim_{N,M} \mathrm{Shv}_{\mathbf{L}_{\widehat{Q}_{N,M}}}^0(G_N\times \mathbf{R}^M\times \mathbf{R}_s;\mathrm{Sp})\Bigr) \end{align}that induces the identity functor on the common underlying module category
5.4 Composite correspondences
Let ![]() $(L,(0,p_0))$ be a germ of smooth Lagrangian in
$(L,(0,p_0))$ be a germ of smooth Lagrangian in ![]() $T^*\mathbf {R}^{M+k}$, whose tangent space at
$T^*\mathbf {R}^{M+k}$, whose tangent space at ![]() $(0,p_0)$ intersect the tangent space of the cotangent fiber in dimension
$(0,p_0)$ intersect the tangent space of the cotangent fiber in dimension ![]() $k$, equivalently
$k$, equivalently ![]() $\dim \pi _*T_{(0,p_0)}L=M$. We will view
$\dim \pi _*T_{(0,p_0)}L=M$. We will view ![]() $\pi _*T_{(0,p_0)}L\cong \mathbf {R}^M$ as a subspace of
$\pi _*T_{(0,p_0)}L\cong \mathbf {R}^M$ as a subspace of ![]() $\mathbf {R}^{M+k}$ and we will think of
$\mathbf {R}^{M+k}$ and we will think of ![]() $\mathbf {R}^{M+k}$ as the product
$\mathbf {R}^{M+k}$ as the product ![]() $(\pi _*T_{(0,p_0)}L)\times (\pi _*T_{(0,p_0)}L)^{\perp }$.
$(\pi _*T_{(0,p_0)}L)\times (\pi _*T_{(0,p_0)}L)^{\perp }$.
In the following, to make the exposition simpler, we assume without loss of generality that ![]() $p_0=0$ and
$p_0=0$ and ![]() $p_1=0$. Note from (5.1.1), the shift of
$p_1=0$. Note from (5.1.1), the shift of ![]() $p_0$ and
$p_0$ and ![]() $p_1$ to
$p_1$ to ![]() $0$ only changes (5.1.1) by a linear function in
$0$ only changes (5.1.1) by a linear function in ![]() $\mathbf {q}_0, \mathbf {q}_1$, so it does not cause any essential difference. Assume that we have chosen
$\mathbf {q}_0, \mathbf {q}_1$, so it does not cause any essential difference. Assume that we have chosen ![]() $A_S$ as in Proposition 5.1(a) such that
$A_S$ as in Proposition 5.1(a) such that
for ![]() $\mathbf {q}_0$ in
$\mathbf {q}_0$ in ![]() $\pi _*T_{(0,0)}L$, and let
$\pi _*T_{(0,0)}L$, and let ![]() $\mathbf {L}_{01}$ be the corresponding Morse transformation (i.e. the negative conormal of (5.1.1)). It is easy to check that the resulting germ of Lagrangian
$\mathbf {L}_{01}$ be the corresponding Morse transformation (i.e. the negative conormal of (5.1.1)). It is easy to check that the resulting germ of Lagrangian ![]() $(L_1,(0,0))$ has tangent space
$(L_1,(0,0))$ has tangent space ![]() $T_{(0,0)}L_1$ equal to the tangent space at
$T_{(0,0)}L_1$ equal to the tangent space at ![]() $(0,0)$ of the graph of the differential of
$(0,0)$ of the graph of the differential of ![]() $-\frac {1}{2}|\mathrm {proj}_{\mathbf {R}^M}\mathbf {q}_0|^2$, where
$-\frac {1}{2}|\mathrm {proj}_{\mathbf {R}^M}\mathbf {q}_0|^2$, where ![]() $\mathrm {proj}_{\mathbf {R}^M}$ means the orthogonal projection to
$\mathrm {proj}_{\mathbf {R}^M}$ means the orthogonal projection to ![]() $\mathbf {R}^M\cong \pi _*T_{(0,0)}L$. Motivated by Proposition 5.1(c), we consider the following diagram of composite correspondences (from right to left):
$\mathbf {R}^M\cong \pi _*T_{(0,0)}L$. Motivated by Proposition 5.1(c), we consider the following diagram of composite correspondences (from right to left):

where ![]() $p_{0,A_S}, p_{1,A_S}$ are the natural projections, and
$p_{0,A_S}, p_{1,A_S}$ are the natural projections, and
 \begin{align*} & p_{0,VG_N}: (A, \mathbf{p}, \mathbf{q}_1, t_1)\mapsto (\mathbf{q}_1, t_1),\\ & p_{1,VG_N}: (A, \mathbf{p}, \mathbf{q}_1,t_1)\mapsto (A, \widetilde{\mathbf{q}}_1=\mathbf{q}_1+2\mathbf{p}, \widetilde{t}_1=t_1+A(\mathbf{p})). \end{align*}
\begin{align*} & p_{0,VG_N}: (A, \mathbf{p}, \mathbf{q}_1, t_1)\mapsto (\mathbf{q}_1, t_1),\\ & p_{1,VG_N}: (A, \mathbf{p}, \mathbf{q}_1,t_1)\mapsto (A, \widetilde{\mathbf{q}}_1=\mathbf{q}_1+2\mathbf{p}, \widetilde{t}_1=t_1+A(\mathbf{p})). \end{align*}
Let
 \begin{align*} &\widetilde{\pi}_{N,M}: X_{012}=VG_N\times\pi(\mathbf{L}_{01})\rightarrow G_N\times \mathbf{R}^{M+k}\times \mathbf{R}_{t_0}\times \mathbf{R}^{M+k}\times \mathbf{R}_{\widetilde{t}_1}\\ &(A, \mathbf{p}, t_0,t_1, \mathbf{q}_0,\mathbf{q}_1)\mapsto (A, t_0,\widetilde{t}_1=t_1+A(\mathbf{p}), \mathbf{q}_0, \widetilde{\mathbf{q}}_1=\mathbf{q}_1+2\mathbf{p}) \end{align*}
\begin{align*} &\widetilde{\pi}_{N,M}: X_{012}=VG_N\times\pi(\mathbf{L}_{01})\rightarrow G_N\times \mathbf{R}^{M+k}\times \mathbf{R}_{t_0}\times \mathbf{R}^{M+k}\times \mathbf{R}_{\widetilde{t}_1}\\ &(A, \mathbf{p}, t_0,t_1, \mathbf{q}_0,\mathbf{q}_1)\mapsto (A, t_0,\widetilde{t}_1=t_1+A(\mathbf{p}), \mathbf{q}_0, \widetilde{\mathbf{q}}_1=\mathbf{q}_1+2\mathbf{p}) \end{align*}
be the projection. Let ![]() $H_{A_S,G_N}$ denote the hypersurface
$H_{A_S,G_N}$ denote the hypersurface
in ![]() $G_N\times \mathbf {R}^{M+k}\times \mathbf {R}_{t_0}\times \mathbf {R}^{M+k}\times \mathbf {R}_{\widetilde {t}_1}$, and consider the (global) correspondence
$G_N\times \mathbf {R}^{M+k}\times \mathbf {R}_{t_0}\times \mathbf {R}^{M+k}\times \mathbf {R}_{\widetilde {t}_1}$, and consider the (global) correspondence

where ![]() $p_{0,H_{A_S,G_N}}$ and
$p_{0,H_{A_S,G_N}}$ and ![]() $p_{1,H_{A_S,G_N}}$ are the obvious projections. Let
$p_{1,H_{A_S,G_N}}$ are the obvious projections. Let ![]() $\mathbf {L}_{1,G_N}$ be the conic Lagrangian in
$\mathbf {L}_{1,G_N}$ be the conic Lagrangian in ![]() $T^{*,<0}(G_N\times \mathbf {R}^{M+k}\times \mathbf {R}_{\widetilde {t}_1})$ assembled from the family of (germs of) conic Lagrangians in
$T^{*,<0}(G_N\times \mathbf {R}^{M+k}\times \mathbf {R}_{\widetilde {t}_1})$ assembled from the family of (germs of) conic Lagrangians in ![]() $T^{*,<0}(\mathbf {R}^{M+k}\times \mathbf {R}_{\widetilde {t}_1})$ which are the image of
$T^{*,<0}(\mathbf {R}^{M+k}\times \mathbf {R}_{\widetilde {t}_1})$ which are the image of ![]() $\mathbf {L}$ under the family of Morse transformations given by the negative conormal of (5.4.3) over
$\mathbf {L}$ under the family of Morse transformations given by the negative conormal of (5.4.3) over ![]() $A\in G_N$.
$A\in G_N$.
Lemma 5.9 We have ![]() $\widetilde {\pi }_{N,M}$ is proper, and
$\widetilde {\pi }_{N,M}$ is proper, and
in
In particular, we have a canonical isomorphism of functors
 \begin{align*} &(p_{1,H_{A_S,G_N}})_*p_{0,H_{A_S,G_N}}^!\simeq (p_{1,VG_N})_*p_{0,VG_N}^!(p_{1,A_S})_*p_{0,A_S}^!:\\ &\mathrm{Shv}_{\mathbf{L}}^0(\mathbf{R}^{M+k}_{\mathbf{q}_0}\times \mathbf{R}_{t_0})\rightarrow \mathrm{Shv}_{\mathbf{L}_{1,G_N}}^0(G_N\times \mathbf{R}_{\widetilde{\mathbf{q}}_1}^{M+k}\times \mathbf{R}_{\tilde{t}_1}). \end{align*}
\begin{align*} &(p_{1,H_{A_S,G_N}})_*p_{0,H_{A_S,G_N}}^!\simeq (p_{1,VG_N})_*p_{0,VG_N}^!(p_{1,A_S})_*p_{0,A_S}^!:\\ &\mathrm{Shv}_{\mathbf{L}}^0(\mathbf{R}^{M+k}_{\mathbf{q}_0}\times \mathbf{R}_{t_0})\rightarrow \mathrm{Shv}_{\mathbf{L}_{1,G_N}}^0(G_N\times \mathbf{R}_{\widetilde{\mathbf{q}}_1}^{M+k}\times \mathbf{R}_{\tilde{t}_1}). \end{align*}
Proof. We look at the image and the fibers of ![]() $\widetilde {\pi }_{N,M}$. Fixing
$\widetilde {\pi }_{N,M}$. Fixing ![]() $(A,t_0,\widetilde {t}_1, \mathbf {q}_0, \widetilde {\mathbf {q}}_1)$ in the target, the fiber over it consists of points satisfying the equation
$(A,t_0,\widetilde {t}_1, \mathbf {q}_0, \widetilde {\mathbf {q}}_1)$ in the target, the fiber over it consists of points satisfying the equation
 \begin{align*}
&\widetilde{t}_1-t_0+\tfrac{1}{2}A_S(\mathbf{q}_0)-\widetilde{\mathbf{q}}_1\cdot\mathbf{q}_0+2\mathbf{p}\cdot
\mathbf{q}_0-A(\mathbf{p})=0\\ \Leftrightarrow\ &|\mathbf{p}-\mathbf{q}_0^A|^2=\widetilde{t}_1-t_0+\tfrac{1}{2}A_S(\mathbf{q}_0)-\widetilde{\mathbf{q}}_1\cdot\mathbf{q}_0+|\mathbf{q}_0^A|^2.
\end{align*}
\begin{align*}
&\widetilde{t}_1-t_0+\tfrac{1}{2}A_S(\mathbf{q}_0)-\widetilde{\mathbf{q}}_1\cdot\mathbf{q}_0+2\mathbf{p}\cdot
\mathbf{q}_0-A(\mathbf{p})=0\\ \Leftrightarrow\ &|\mathbf{p}-\mathbf{q}_0^A|^2=\widetilde{t}_1-t_0+\tfrac{1}{2}A_S(\mathbf{q}_0)-\widetilde{\mathbf{q}}_1\cdot\mathbf{q}_0+|\mathbf{q}_0^A|^2.
\end{align*}
Thus, the image of ![]() $\widetilde {\pi }_{N,M}$ is along
$\widetilde {\pi }_{N,M}$ is along
and the fiber is a point (respectively, a sphere) when (5.4.5) is an equality (respectively, inequality). Hence, the lemma follows easily.
Note that ![]() $(\mathbf {L}_1, (0,0;t_1=0,-dt_1))$ has the same tangent space as
$(\mathbf {L}_1, (0,0;t_1=0,-dt_1))$ has the same tangent space as ![]() $\mathbf {L}_{Q_M^0}\times T_{\mathbf {R}^k}^*\mathbf {R}^{k}$ at
$\mathbf {L}_{Q_M^0}\times T_{\mathbf {R}^k}^*\mathbf {R}^{k}$ at ![]() $(0,0; t_1=0,-dt_1)$, thus we have a commutative diagram
$(0,0; t_1=0,-dt_1)$, thus we have a commutative diagram

which represents a canonical isomorphism between the left vertical arrow and the right vertical arrow as objects in ![]() $\mathrm {Fun}(\Delta ^1, \mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$.
$\mathrm {Fun}(\Delta ^1, \mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$.
5.5 The process of stabilization
Now consider the family of (5.4.2) over ![]() $(\mathbf {N}\times \mathbf {N})^{\geq \mathrm {dgnl}}_{(N,M)/}$.
$(\mathbf {N}\times \mathbf {N})^{\geq \mathrm {dgnl}}_{(N,M)/}$.
(i) For each
 $(N',M')\geq (N,M)$, set
and let
$(N',M')\geq (N,M)$, set
and let \begin{gather*} L^{M'}=L\times
T_{\mathbf{R}^{M'-M}}^*\mathbf{R}^{M'-M}\subset
T^*\mathbf{R}^{M'+k},\\
A^{M'}_S(\mathbf{q}_0)=A_S(\mathrm{proj}_{\mathbf{R}^{M+k}}\mathbf{q}_0)-|\mathrm{proj}_{\mathbf{R}^{M'-M}}\mathbf{q}_0|^2
\end{gather*}
be the negative conormal bundle of
\begin{gather*} L^{M'}=L\times
T_{\mathbf{R}^{M'-M}}^*\mathbf{R}^{M'-M}\subset
T^*\mathbf{R}^{M'+k},\\
A^{M'}_S(\mathbf{q}_0)=A_S(\mathrm{proj}_{\mathbf{R}^{M+k}}\mathbf{q}_0)-|\mathrm{proj}_{\mathbf{R}^{M'-M}}\mathbf{q}_0|^2
\end{gather*}
be the negative conormal bundle of \[ \mathbf{L}_{01}^{M'}\subset (T^{*,<0}(\mathbf{R}_{\mathbf{q}_0}^{M'+k}\times \mathbf{R}_{t_0}))^-\times T^{*,<0}(\mathbf{R}_{\mathbf{q}_1}^{M'+k}\times \mathbf{R}_{t_1}) \]
The factors
\[ \mathbf{L}_{01}^{M'}\subset (T^{*,<0}(\mathbf{R}_{\mathbf{q}_0}^{M'+k}\times \mathbf{R}_{t_0}))^-\times T^{*,<0}(\mathbf{R}_{\mathbf{q}_1}^{M'+k}\times \mathbf{R}_{t_1}) \]
The factors \[ t_1-t_0+\tfrac{1}{2}A_S^{M'}(\mathbf{q}_0)-\mathbf{q}_0\cdot\mathbf{q}_1=0. \]
\[ t_1-t_0+\tfrac{1}{2}A_S^{M'}(\mathbf{q}_0)-\mathbf{q}_0\cdot\mathbf{q}_1=0. \]
 $\mathbf {R}^{M+k}$,
$\mathbf {R}^{M+k}$,  $VG_N$, and
$VG_N$, and  $G_N$ in the entries of (5.4.2) are replaced by
$G_N$ in the entries of (5.4.2) are replaced by  $\mathbf {R}^{M'+k}$,
$\mathbf {R}^{M'+k}$,  $VG_{N'}$, and
$VG_{N'}$, and  $G_{N'}$, respectively. The morphisms
$G_{N'}$, respectively. The morphisms  $p_{i,VG_N}$ and
$p_{i,VG_N}$ and  $p_{i,A_S}$ in the diagram are replaced by their obvious extensions, denoted by
$p_{i,A_S}$ in the diagram are replaced by their obvious extensions, denoted by  $p_{i,VG_{N'}}$ and
$p_{i,VG_{N'}}$ and  $p_{i,A^{M'}_S}$, respectively.
$p_{i,A^{M'}_S}$, respectively.(ii) For each morphism
 $(N_1,M_1)\leq (N_2,M_2)$ in
$(N_1,M_1)\leq (N_2,M_2)$ in  $(\mathbf {N}\times \mathbf {N})^{\geq \mathrm {dgnl}}_{(N,M)/}$, the connecting morphisms between the corresponding entries in the diagrams (5.4.2) are the obvious embeddings induced from
$(\mathbf {N}\times \mathbf {N})^{\geq \mathrm {dgnl}}_{(N,M)/}$, the connecting morphisms between the corresponding entries in the diagrams (5.4.2) are the obvious embeddings induced from
 \[ \mathbf{R}^{M_1+k}\hookrightarrow \mathbf{R}^{M_2+k},\ VG_{N_1}\hookrightarrow VG_{N_2},\ G_{N_1}\hookrightarrow G_{N_2}. \]
\[ \mathbf{R}^{M_1+k}\hookrightarrow \mathbf{R}^{M_2+k},\ VG_{N_1}\hookrightarrow VG_{N_2},\ G_{N_1}\hookrightarrow G_{N_2}. \]
First, for each ![]() $(N_1,M_1)\leq (N_2, M_2)$, the diagram
$(N_1,M_1)\leq (N_2, M_2)$, the diagram

is Cartesian.
Second, we look at the following diagram for ![]() $(N_1,M_1)\leq (N_2,M_2)$:
$(N_1,M_1)\leq (N_2,M_2)$:

in which
 \begin{align*} Y_{M_1,M_2}&=\{t_1-t_0+\tfrac{1}{2}A_S^{M_1}(\mathrm{proj}_{\mathbf{R}^{M_1+k}}\mathbf{q}_0)-\tfrac{1}{2}|\mathrm{proj}_{\mathbf{R}^{M_2-M_1}}\mathbf{q}_0|^2-\mathbf{q}_1\cdot \mathrm{proj}_{\mathbf{R}^{M_1+k}}\mathbf{q}_0=0\}\\ &\subset \mathbf{R}^{M_2+k}_{\mathbf{q}_0}\times \mathbf{R}^{M_1+k}_{\mathbf{q}_1}\times \mathbf{R}_{t_0}\times\mathbf{R}_{t_1}, \end{align*}
\begin{align*} Y_{M_1,M_2}&=\{t_1-t_0+\tfrac{1}{2}A_S^{M_1}(\mathrm{proj}_{\mathbf{R}^{M_1+k}}\mathbf{q}_0)-\tfrac{1}{2}|\mathrm{proj}_{\mathbf{R}^{M_2-M_1}}\mathbf{q}_0|^2-\mathbf{q}_1\cdot \mathrm{proj}_{\mathbf{R}^{M_1+k}}\mathbf{q}_0=0\}\\ &\subset \mathbf{R}^{M_2+k}_{\mathbf{q}_0}\times \mathbf{R}^{M_1+k}_{\mathbf{q}_1}\times \mathbf{R}_{t_0}\times\mathbf{R}_{t_1}, \end{align*}
and ![]() $\iota _{M_1}: \pi (\mathbf {L}^{M_1}_{01})\rightarrow Y_{M_1,M_2}$ represents the deficiency of the outer square from being Cartesian. Since the projection
$\iota _{M_1}: \pi (\mathbf {L}^{M_1}_{01})\rightarrow Y_{M_1,M_2}$ represents the deficiency of the outer square from being Cartesian. Since the projection
 \begin{gather*} \widetilde{\pi}_{Y,
M_1,M_2}: Y_{M_1,M_2}\rightarrow
\mathbf{R}_{\mathbf{q}_0}^{M_1+k}\times
\mathbf{R}_{q_1}^{M_1+k}\times \mathbf{R}_{t_0}\times
\mathbf{R}_{t_1}\\
(\mathbf{q}_0,\mathbf{q}_1,t_0,t_1)\mapsto
(\mathrm{proj}_{\mathbf{R}^{M_1+k}}\mathbf{q}_0,\mathbf{q}_1,
t_0,t_1) \end{gather*}
\begin{gather*} \widetilde{\pi}_{Y,
M_1,M_2}: Y_{M_1,M_2}\rightarrow
\mathbf{R}_{\mathbf{q}_0}^{M_1+k}\times
\mathbf{R}_{q_1}^{M_1+k}\times \mathbf{R}_{t_0}\times
\mathbf{R}_{t_1}\\
(\mathbf{q}_0,\mathbf{q}_1,t_0,t_1)\mapsto
(\mathrm{proj}_{\mathbf{R}^{M_1+k}}\mathbf{q}_0,\mathbf{q}_1,
t_0,t_1) \end{gather*}
behaves similarly as ![]() $\widetilde {\pi }_{N,M}$ (see the proof of Lemma 5.9) in the sense that its image is
$\widetilde {\pi }_{N,M}$ (see the proof of Lemma 5.9) in the sense that its image is
with fiber either a point or a sphere given by ![]() $\frac {1}{2}|\mathrm {proj}_{\mathbf {R}^{M_2-M_1}}\mathbf {q}_0|^2=r$, we have
$\frac {1}{2}|\mathrm {proj}_{\mathbf {R}^{M_2-M_1}}\mathbf {q}_0|^2=r$, we have
in ![]() $\mathrm {Shv}(\mathbf {R}_{\mathbf {q}_0}^{M_1+k}\times \mathbf {R}_{q_1}^{M_1+k}\times \mathbf {R}_{t_0}\times \mathbf {R}_{t_1};\mathrm {Sp})/\mathrm {Shv}_{\leq 0}(\mathbf {R}_{\mathbf {q}_0}^{M_1+k}\times \mathbf {R}_{q_1}^{M_1+k}\times \mathbf {R}_{t_0}\times \mathbf {R}_{t_1};\mathrm {Sp})$. Therefore, we have a canonical isomorphism of functors
$\mathrm {Shv}(\mathbf {R}_{\mathbf {q}_0}^{M_1+k}\times \mathbf {R}_{q_1}^{M_1+k}\times \mathbf {R}_{t_0}\times \mathbf {R}_{t_1};\mathrm {Sp})/\mathrm {Shv}_{\leq 0}(\mathbf {R}_{\mathbf {q}_0}^{M_1+k}\times \mathbf {R}_{q_1}^{M_1+k}\times \mathbf {R}_{t_0}\times \mathbf {R}_{t_1};\mathrm {Sp})$. Therefore, we have a canonical isomorphism of functors
 \begin{align*}
(p_{1,A_S^{M_1}})_*\iota_{01,M_1}^!&\simeq \jmath_{\mathbf{q}_1,M_1}^!(p_{1,A_S^{M_2}})_*:\\
\mathrm{Loc}(\pi(\mathbf{L}_{01}^{M_2});\mathrm{Sp})&\simeq
\mathrm{Shv}_{\mathbf{L}_{01}^{M_2}}^0(\mathbf{R}_{\mathbf{q}_0}^{M_2+k}\times\mathbf{R}_{\mathbf{q}_1}^{M_2+k}\times\mathbf{R}_{t_0}\times\mathbf{R}_{t_1};\mathrm{Sp})
\rightarrow\mathrm{Shv}_{\mathbf{L}_1^{M_1}}^0(\mathbf{R}_{\mathbf{q}_1}^{M_1+k}\times\mathbf{R}_{t_1};\mathrm{Sp}).
\end{align*}
\begin{align*}
(p_{1,A_S^{M_1}})_*\iota_{01,M_1}^!&\simeq \jmath_{\mathbf{q}_1,M_1}^!(p_{1,A_S^{M_2}})_*:\\
\mathrm{Loc}(\pi(\mathbf{L}_{01}^{M_2});\mathrm{Sp})&\simeq
\mathrm{Shv}_{\mathbf{L}_{01}^{M_2}}^0(\mathbf{R}_{\mathbf{q}_0}^{M_2+k}\times\mathbf{R}_{\mathbf{q}_1}^{M_2+k}\times\mathbf{R}_{t_0}\times\mathbf{R}_{t_1};\mathrm{Sp})
\rightarrow\mathrm{Shv}_{\mathbf{L}_1^{M_1}}^0(\mathbf{R}_{\mathbf{q}_1}^{M_1+k}\times\mathbf{R}_{t_1};\mathrm{Sp}).
\end{align*}
Similarly, we can consider the family of diagrams (5.4.4) over ![]() $(\mathbf {N}\times \mathbf {N})^{\geq \mathrm {dgnl}}_{(N,M)/}$, where for each
$(\mathbf {N}\times \mathbf {N})^{\geq \mathrm {dgnl}}_{(N,M)/}$, where for each ![]() $(N',M')$,
$(N',M')$, ![]() $H_{A_S, G_N}$ is replaced by
$H_{A_S, G_N}$ is replaced by ![]() $H_{A_S^{M'},G_{N'}}$ (defined in (5.4.3)),
$H_{A_S^{M'},G_{N'}}$ (defined in (5.4.3)), ![]() $\mathbf {R}_{\widetilde {\mathbf {q}}_1}^{M+k}$ is replaced by
$\mathbf {R}_{\widetilde {\mathbf {q}}_1}^{M+k}$ is replaced by ![]() $\mathbf {R}_{\widetilde {\mathbf {q}}_1}^{M'+k}$, and
$\mathbf {R}_{\widetilde {\mathbf {q}}_1}^{M'+k}$, and ![]() $G_N$ is replaced by
$G_N$ is replaced by ![]() $G_{N'}$. The connecting morphisms over
$G_{N'}$. The connecting morphisms over ![]() $(N_1,M_1)\rightarrow (N_2, M_2)$ are directly induced from the embeddings
$(N_1,M_1)\rightarrow (N_2, M_2)$ are directly induced from the embeddings ![]() $G_{N_1}\hookrightarrow G_{N_2}$ and
$G_{N_1}\hookrightarrow G_{N_2}$ and ![]() $\mathbf {R}^{M_1+k}\hookrightarrow \mathbf {R}^{M_2+k}$. Similar to (5.5.1), the diagram
$\mathbf {R}^{M_1+k}\hookrightarrow \mathbf {R}^{M_2+k}$. Similar to (5.5.1), the diagram

is not Cartesian, but the deficiency of it from being Cartesian induces an invertible 2-morphism on the localized sheaf categories, hence we have a canonical isomorphism of functors
 \begin{align*} &(p_{1,H_{\scriptscriptstyle{A_S^{M_1}}, G_{N_1}}})_*\iota_{H,M_1,M_2}^!\simeq \jmath_{G,N_1,N_2}^!(p_{1,H_{\scriptscriptstyle{A_S^{M_2}}, G_{N_2}}})_*: \\ &\mathrm{Loc}(H_{A_S^{M_2}, G_{N_2}};\mathrm{Sp})\rightarrow \mathrm{Shv}_{\mathbf{L}_{\widehat{Q}_{N_2, M_2}}}^0(G_{N_2}\times\mathbf{R}^{M_2+k}_{\widetilde{\mathbf{q}}_1}\times \mathbf{R}_{\widetilde{t}_1}; \mathrm{Sp}). \end{align*}
\begin{align*} &(p_{1,H_{\scriptscriptstyle{A_S^{M_1}}, G_{N_1}}})_*\iota_{H,M_1,M_2}^!\simeq \jmath_{G,N_1,N_2}^!(p_{1,H_{\scriptscriptstyle{A_S^{M_2}}, G_{N_2}}})_*: \\ &\mathrm{Loc}(H_{A_S^{M_2}, G_{N_2}};\mathrm{Sp})\rightarrow \mathrm{Shv}_{\mathbf{L}_{\widehat{Q}_{N_2, M_2}}}^0(G_{N_2}\times\mathbf{R}^{M_2+k}_{\widetilde{\mathbf{q}}_1}\times \mathbf{R}_{\widetilde{t}_1}; \mathrm{Sp}). \end{align*}
Now applying the dual version of ![]() $\mathrm {ShvSp}_{\mathsf {all},\mathsf {all}}^{\mathsf {prop}}$ (whose target is
$\mathrm {ShvSp}_{\mathsf {all},\mathsf {all}}^{\mathsf {prop}}$ (whose target is ![]() $\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}}$) to the family of diagrams over
$\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}}$) to the family of diagrams over ![]() $(\mathbf {N}\times \mathbf {N})^{\geq \mathrm {dgnl}}_{(N,M)/}$, passing to the localized sheaf categories and taking limits over
$(\mathbf {N}\times \mathbf {N})^{\geq \mathrm {dgnl}}_{(N,M)/}$, passing to the localized sheaf categories and taking limits over ![]() $(\mathbf {N}\times \mathbf {N})^{\geq \mathrm {dgnl}}_{(N,M)/}$, we get a canonical isomorphism of functors
$(\mathbf {N}\times \mathbf {N})^{\geq \mathrm {dgnl}}_{(N,M)/}$, we get a canonical isomorphism of functors
 \begin{align*} &(p_{1,H_{A^{\mathit{st}}_S,G}})_*p_{0,H_{A^{\mathit{st}}_S,G}}^!\simeq (p_{1,VG})_*p_{0,VG}^!(p_{1,A^{\mathit{st}}_S})_*p_{0,A^{\mathit{st}}_S}^!:\\ &\varprojlim_{M'}\mathrm{Shv}_{\mathbf{L}^{M'}}^0(\mathbf{R}^{M'+k}_{\mathbf{q}_0}\times \mathbf{R}_{t_0};\mathrm{Sp})\rightarrow \varprojlim_{N',M'}\mathrm{Shv}_{\mathbf{L}_{1,G_{N'}}}^0(G_{N'}\times \mathbf{R}_{\widetilde{\mathbf{q}}_1}^{M'+k}\times \mathbf{R}_{\tilde{t}_1};\mathrm{Sp}). \end{align*}
\begin{align*} &(p_{1,H_{A^{\mathit{st}}_S,G}})_*p_{0,H_{A^{\mathit{st}}_S,G}}^!\simeq (p_{1,VG})_*p_{0,VG}^!(p_{1,A^{\mathit{st}}_S})_*p_{0,A^{\mathit{st}}_S}^!:\\ &\varprojlim_{M'}\mathrm{Shv}_{\mathbf{L}^{M'}}^0(\mathbf{R}^{M'+k}_{\mathbf{q}_0}\times \mathbf{R}_{t_0};\mathrm{Sp})\rightarrow \varprojlim_{N',M'}\mathrm{Shv}_{\mathbf{L}_{1,G_{N'}}}^0(G_{N'}\times \mathbf{R}_{\widetilde{\mathbf{q}}_1}^{M'+k}\times \mathbf{R}_{\tilde{t}_1};\mathrm{Sp}). \end{align*}
Lastly, using diagram (5.4.6) and Corollary 4.16, we immediately get the following.
Theorem 5.10 The correspondences (5.4.4) for all ![]() $M'\geq N'$ give rise to a canonical equivalence
$M'\geq N'$ give rise to a canonical equivalence
 \begin{align*}
\varprojlim_{M'}\mathrm{Shv}_{\mathbf{L}^{M'}}^0(\mathbf{R}^{M'+k}\times
\mathbf{R}_{t_0};\mathrm{Sp})\overset{\sim}{\longrightarrow}\ &\mathrm{ Loc}(\widehat{Q};\mathrm{Sp})^J \\
&\simeq \Big(\varprojlim_{N,M}
\mathrm{Shv}_{\mathbf{L}_{\widehat{Q}_{N,M}}}^0(G_N\times
\mathbf{R}^M\times \mathbf{R}_s;\mathrm{Sp})\Big)^J.
\end{align*}
\begin{align*}
\varprojlim_{M'}\mathrm{Shv}_{\mathbf{L}^{M'}}^0(\mathbf{R}^{M'+k}\times
\mathbf{R}_{t_0};\mathrm{Sp})\overset{\sim}{\longrightarrow}\ &\mathrm{ Loc}(\widehat{Q};\mathrm{Sp})^J \\
&\simeq \Big(\varprojlim_{N,M}
\mathrm{Shv}_{\mathbf{L}_{\widehat{Q}_{N,M}}}^0(G_N\times
\mathbf{R}^M\times \mathbf{R}_s;\mathrm{Sp})\Big)^J.
\end{align*}
5.6 Compatibility among different choices of  $A_S$
$A_S$
In this subsection, we briefly discuss the compatibility of the above results for the particular choice of ![]() $A_S$ (5.4.1), especially Theorem 5.10, with other choices of
$A_S$ (5.4.1), especially Theorem 5.10, with other choices of ![]() $A_S$ by adding to it some
$A_S$ by adding to it some ![]() $A\in G_N$. We will go into more details of this in [Reference JinJin20].
$A\in G_N$. We will go into more details of this in [Reference JinJin20].
For any ![]() $A\in G_N$, we define the
$A\in G_N$, we define the ![]() $\mathrm {Fin}_*$-object
$\mathrm {Fin}_*$-object ![]() $(G_N^{A^\perp })^\bullet$ in
$(G_N^{A^\perp })^\bullet$ in ![]() $\mathrm {S}_{\mathrm {LCH}}$ to be
$\mathrm {S}_{\mathrm {LCH}}$ to be
Similarly, we define
It is clear that the obvious inclusions
 \begin{align*} &\iota_{G_N^{A^\perp}}: (G_N^{A^\perp})^\bullet\hookrightarrow G_N^\bullet \\ &\iota_{VG_N^{A^\perp}}: (VG_N^{A^\perp})^\bullet\hookrightarrow VG_N^\bullet \end{align*}
\begin{align*} &\iota_{G_N^{A^\perp}}: (G_N^{A^\perp})^\bullet\hookrightarrow G_N^\bullet \\ &\iota_{VG_N^{A^\perp}}: (VG_N^{A^\perp})^\bullet\hookrightarrow VG_N^\bullet \end{align*}
thought as correspondences
 \begin{align*} &(G_N^{A^\perp})^\bullet\overset{id}{\leftarrow}(G_N^{A^\perp})^\bullet\hookrightarrow G_N^\bullet \\ &(VG_N^{A^\perp})^\bullet\overset{id}{\leftarrow}(VG_N^{A^\perp})^\bullet\hookrightarrow VG_N^\bullet \end{align*}
\begin{align*} &(G_N^{A^\perp})^\bullet\overset{id}{\leftarrow}(G_N^{A^\perp})^\bullet\hookrightarrow G_N^\bullet \\ &(VG_N^{A^\perp})^\bullet\overset{id}{\leftarrow}(VG_N^{A^\perp})^\bullet\hookrightarrow VG_N^\bullet \end{align*}
induce morphisms in ![]() $\mathrm {CAlg}(\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}})$, which induce the following commutative diagram of equivalences.
$\mathrm {CAlg}(\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}})$, which induce the following commutative diagram of equivalences.

Let
 \begin{align*}
\widehat{Q}_{N,M}^{A^{\perp}}&=\{(A_1,\mathbf{q},s)\in
G_N^{A^\perp}\times \mathbf{R}^M\times \mathbf{R}_s:
s<-\tfrac{1}{2}|\mathbf{q}|^2+(A_1+A)(\mathbf{q})\},\\
Q_M^{0,A}&=\{(\mathbf{q},s)\in
\mathbf{R}^M\times\mathbf{R}_s:
s<-\tfrac{1}{2}|\mathbf{q}|^2+A(\mathbf{q})\}.
\end{align*}
\begin{align*}
\widehat{Q}_{N,M}^{A^{\perp}}&=\{(A_1,\mathbf{q},s)\in
G_N^{A^\perp}\times \mathbf{R}^M\times \mathbf{R}_s:
s<-\tfrac{1}{2}|\mathbf{q}|^2+(A_1+A)(\mathbf{q})\},\\
Q_M^{0,A}&=\{(\mathbf{q},s)\in
\mathbf{R}^M\times\mathbf{R}_s:
s<-\tfrac{1}{2}|\mathbf{q}|^2+A(\mathbf{q})\}.
\end{align*}
Consider the Cartesian diagram

where
 \begin{align*} &\jmath^0_{M,A}: (A_1,\mathbf{p}_1,\mathbf{p}\in A, \mathbf{q},s)\mapsto (A_1, \mathbf{p}_1, \mathbf{q},s),\\ &\widehat{\jmath}_{M,A}: (\mathbf{p}, A_1, \mathbf{q}, s)\mapsto (A_1\oplus A, \mathbf{q}, s+A(\mathbf{p})),\\ &\psi_{M,A}: (A_1,\mathbf{p}_1,\mathbf{p}\in A, \mathbf{q},s)\mapsto (\mathbf{p},A_1\oplus A, \mathbf{q}+\mathbf{p}_1, s+A_1(\mathbf{p}_1)). \end{align*}
\begin{align*} &\jmath^0_{M,A}: (A_1,\mathbf{p}_1,\mathbf{p}\in A, \mathbf{q},s)\mapsto (A_1, \mathbf{p}_1, \mathbf{q},s),\\ &\widehat{\jmath}_{M,A}: (\mathbf{p}, A_1, \mathbf{q}, s)\mapsto (A_1\oplus A, \mathbf{q}, s+A(\mathbf{p})),\\ &\psi_{M,A}: (A_1,\mathbf{p}_1,\mathbf{p}\in A, \mathbf{q},s)\mapsto (\mathbf{p},A_1\oplus A, \mathbf{q}+\mathbf{p}_1, s+A_1(\mathbf{p}_1)). \end{align*}
We view ![]() $VG^{A^\perp }_N\times A\times Q^0_M$ (respectively,
$VG^{A^\perp }_N\times A\times Q^0_M$ (respectively, ![]() $VG_N\times Q_M^0$) as a free module of
$VG_N\times Q_M^0$) as a free module of ![]() $(VG^{A^\perp }_N)^\bullet$ (respectively,
$(VG^{A^\perp }_N)^\bullet$ (respectively, ![]() $VG_N^\bullet$) in
$VG_N^\bullet$) in ![]() $\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$ generated by
$\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {fib},\mathsf {all}}$ generated by ![]() $A\times Q^0_M$ (respectively,
$A\times Q^0_M$ (respectively, ![]() $Q_M^0$), and
$Q_M^0$), and ![]() $\widehat {Q}^{A^\perp }_{N,M}$ (respectively,
$\widehat {Q}^{A^\perp }_{N,M}$ (respectively, ![]() $\widehat {Q}_{N,M}$) as a module of
$\widehat {Q}_{N,M}$) as a module of ![]() $(VG^{A^\perp })^\bullet$ (respectively,
$(VG^{A^\perp })^\bullet$ (respectively, ![]() $VG^\bullet$) as in Lemma 4.6. The inductive system of (
$VG^\bullet$) as in Lemma 4.6. The inductive system of (
) under inclusions over ![]() $(\mathbf {N}\times \mathbf {N})^{\geq \mathrm {dgnl}}$ gives rise to a functor
$(\mathbf {N}\times \mathbf {N})^{\geq \mathrm {dgnl}}$ gives rise to a functor ![]() $[1]\times [1]^{\rm op}\rightarrow \mathrm {Fun}(I_{\pi _{\dagger} },\mathcal {C})$ (with
$[1]\times [1]^{\rm op}\rightarrow \mathrm {Fun}(I_{\pi _{\dagger} },\mathcal {C})$ (with ![]() $[1]^{\rm op}$ corresponding to the horizontal arrows) that satisfies the properties in Proposition 2.28, hence applying the symmetric monoidal functor
$[1]^{\rm op}$ corresponding to the horizontal arrows) that satisfies the properties in Proposition 2.28, hence applying the symmetric monoidal functor ![]() $\mathrm {Loc}_*^!$ to the diagram and taking the limit over
$\mathrm {Loc}_*^!$ to the diagram and taking the limit over ![]() $(\mathbf {N}\times \mathbf {N})^{\geq \mathrm {dgnl}}$, we get the following commutative diagram in
$(\mathbf {N}\times \mathbf {N})^{\geq \mathrm {dgnl}}$, we get the following commutative diagram in ![]() $\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$.
$\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$.

This canonically induces a commutative diagram of isomorphisms in ![]() $\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$
$\mathcal {M}\mathrm {od}^{N(\mathrm {Fin}_*)}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$

which further induces the following commutative diagram of equivalences.

Acknowledgements
I would like to thank David Nadler, Dima Tamarkin, David Treumann, and Eric Zaslow for their interest and helpful discussions related to this paper. I am also grateful to John Francis, Yifeng Liu, Jacob Lurie, and Nick Rozenblyum for answering several questions on higher category theory and for help with references. I am, in particular, grateful to an anonymous referee for useful comments and suggestions which improved the paper significantly.
Conflicts of interest
None.
Financial support
This work was performed under the support of an NSF grant DMS-1854232.
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.
Appendix A. The Thom construction via correspondences
The goal of the appendix is to give a realization of the Thom construction using the category of correspondences, and to conclude with a proof of Proposition 4.13 that the proposed model of the ![]() $J$-homomorphism from correspondences is equivalent to a standard model.
$J$-homomorphism from correspondences is equivalent to a standard model.
A.1  $\mathcal {V}\mathcal {S}\mathrm {pc}$ and the Thom construction
$\mathcal {V}\mathcal {S}\mathrm {pc}$ and the Thom construction
Let ![]() $\mathcal {V}\mathcal {S}\mathrm {pc}$ be the
$\mathcal {V}\mathcal {S}\mathrm {pc}$ be the ![]() $\infty$-category of pairs
$\infty$-category of pairs ![]() $(V, X)$, where
$(V, X)$, where ![]() $V$ is a (real finite dimensional) vector bundle on
$V$ is a (real finite dimensional) vector bundle on ![]() $X\in \mathcal {S}\mathrm {pc}$, and any morphism
$X\in \mathcal {S}\mathrm {pc}$, and any morphism ![]() $(V, X)$ to
$(V, X)$ to ![]() $(V', Y)$ is given by
$(V', Y)$ is given by ![]() $f: X\rightarrow Y$ and a vector bundle isomorphism
$f: X\rightarrow Y$ and a vector bundle isomorphism ![]() $V\overset {\sim }{\rightarrow } f^*V'$ over
$V\overset {\sim }{\rightarrow } f^*V'$ over ![]() $X$. Equivalently (and more precisely),
$X$. Equivalently (and more precisely), ![]() $\mathcal {V}\mathcal {S}\mathrm {pc}$ is the right fibration (in particular the Cartesian fibration) over
$\mathcal {V}\mathcal {S}\mathrm {pc}$ is the right fibration (in particular the Cartesian fibration) over ![]() $\mathcal {S}\mathrm {pc}$ from the unstraightening of the natural functorFootnote 8
$\mathcal {S}\mathrm {pc}$ from the unstraightening of the natural functorFootnote 8 ![]() $\mathbf {V}: \mathcal {S}\mathrm {pc}^{\rm op}\to \mathrm {Gpd}_\infty$,
$\mathbf {V}: \mathcal {S}\mathrm {pc}^{\rm op}\to \mathrm {Gpd}_\infty$, ![]() $X\mapsto \mathrm {Maps}_{\mathcal {S}\mathrm {pc}}(X,\coprod _nBO(n))$. Equivalently,
$X\mapsto \mathrm {Maps}_{\mathcal {S}\mathrm {pc}}(X,\coprod _nBO(n))$. Equivalently, ![]() $\mathcal {V}\mathcal {S}\mathrm {pc}\simeq \mathcal {S}\mathrm {pc}_{/\coprod _nBO(n)}$. Clearly,
$\mathcal {V}\mathcal {S}\mathrm {pc}\simeq \mathcal {S}\mathrm {pc}_{/\coprod _nBO(n)}$. Clearly, ![]() $\mathcal {V}\mathcal {S}\mathrm {pc}$ has the natural (non-Cartesian) symmetric monoidal structure given by taking product of vector bundles, which corresponds to the right-lax symmetric monoidal functor
$\mathcal {V}\mathcal {S}\mathrm {pc}$ has the natural (non-Cartesian) symmetric monoidal structure given by taking product of vector bundles, which corresponds to the right-lax symmetric monoidal functor ![]() $\mathbf {V}$ using the commutative topological monoid structure on
$\mathbf {V}$ using the commutative topological monoid structure on ![]() $G=\coprod _nBO(n)$.
$G=\coprod _nBO(n)$.
Let ![]() $\mathbf {P}: \mathcal {S}\mathrm {pc}^{\rm op}\to \mathrm {Gpd}_\infty, X\mapsto \mathrm {Maps}(X,\mathrm {Pic}(\mathbf {S}))$. The Thom construction naturally defines a symmetric monoidal functor
$\mathbf {P}: \mathcal {S}\mathrm {pc}^{\rm op}\to \mathrm {Gpd}_\infty, X\mapsto \mathrm {Maps}(X,\mathrm {Pic}(\mathbf {S}))$. The Thom construction naturally defines a symmetric monoidal functor
where ![]() $\mathcal {L}_V$ is the local system of
$\mathcal {L}_V$ is the local system of ![]() $\mathbf {S}$-lines corresponding to the stable sphere fibration associated to
$\mathbf {S}$-lines corresponding to the stable sphere fibration associated to ![]() $V$ (which is equivalent to the
$V$ (which is equivalent to the ![]() $!$-pullback of the ‘universal’ stable sphere fibration over
$!$-pullback of the ‘universal’ stable sphere fibration over ![]() $G$ classified by
$G$ classified by ![]() $J$). Equivalently, using straightening for Cartesian fibrations over
$J$). Equivalently, using straightening for Cartesian fibrations over ![]() $\mathcal {S}\mathrm {pc}$,
$\mathcal {S}\mathrm {pc}$, ![]() $\mathbb {T}^{\mathrm {invt}}$ is corresponding to the natural morphism
$\mathbb {T}^{\mathrm {invt}}$ is corresponding to the natural morphism ![]() $\mathbf {V}\rightarrow \mathbf {P}$ in
$\mathbf {V}\rightarrow \mathbf {P}$ in ![]() $\mathrm {Fun}^{\mathrm {R}\text {-}\mathrm {lax}}((\mathcal {S}\mathrm {pc}^\times )^{\rm op}, \mathrm {Gpd}_\infty ^\times )$, induced by the
$\mathrm {Fun}^{\mathrm {R}\text {-}\mathrm {lax}}((\mathcal {S}\mathrm {pc}^\times )^{\rm op}, \mathrm {Gpd}_\infty ^\times )$, induced by the ![]() $J$-homomorphism
$J$-homomorphism ![]() $\coprod _{n}BO(n)\rightarrow \mathrm {Pic}(\mathbf {S})$ (as an
$\coprod _{n}BO(n)\rightarrow \mathrm {Pic}(\mathbf {S})$ (as an ![]() $E_\infty$-map). We will mostly consider the following version:
$E_\infty$-map). We will mostly consider the following version:
which, of course, contains all the information about ![]() $\mathbb {T}^{\mathrm {invt}}$.
$\mathbb {T}^{\mathrm {invt}}$.
A.2 A realization of the Thom construction using correspondences
Let ![]() $\mathrm {Top}$ be the ordinary 1-category of all CW-complexes. Let
$\mathrm {Top}$ be the ordinary 1-category of all CW-complexes. Let ![]() $\mathrm {V}\mathrm {S}_{\mathrm {LCH}}$ be the ordinary 1-category of pairs
$\mathrm {V}\mathrm {S}_{\mathrm {LCH}}$ be the ordinary 1-category of pairs ![]() $(V, X)$, where
$(V, X)$, where ![]() $X\in \mathrm {S}_{\mathrm {LCH}}$ and
$X\in \mathrm {S}_{\mathrm {LCH}}$ and ![]() $V$ is a vector bundle over
$V$ is a vector bundle over ![]() $X$, and a morphism
$X$, and a morphism ![]() $(V, X)\rightarrow (V',Y)$ is given by a continuous map
$(V, X)\rightarrow (V',Y)$ is given by a continuous map ![]() $f: X\rightarrow Y$ together with a vector bundle isomorphism
$f: X\rightarrow Y$ together with a vector bundle isomorphism ![]() $\varphi : V\rightarrow f^*V'$ over
$\varphi : V\rightarrow f^*V'$ over ![]() $X$. It is clear that
$X$. It is clear that ![]() $\mathrm {V}\mathrm {S}_{\mathrm {LCH}}\rightarrow \mathrm {S}_{\mathrm {LCH}}$ is a Cartesian fibration with fibers discrete groupoids. Similarly, we define
$\mathrm {V}\mathrm {S}_{\mathrm {LCH}}\rightarrow \mathrm {S}_{\mathrm {LCH}}$ is a Cartesian fibration with fibers discrete groupoids. Similarly, we define ![]() $\mathrm {VTop}$ over
$\mathrm {VTop}$ over ![]() $\mathrm {Top}$.
$\mathrm {Top}$.
A.2.1 Definition of  $\mathbb {T}_{\mathrm {VTop}}$
$\mathbb {T}_{\mathrm {VTop}}$
We first define a symmetric monoidal functor ![]() $\mathbb {T}_{\mathrm {VTop}}: \mathrm {VTop}^{\rm op}\to (\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}/}$ using correspondences. We will prove that after passing to a natural localization of
$\mathbb {T}_{\mathrm {VTop}}: \mathrm {VTop}^{\rm op}\to (\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}/}$ using correspondences. We will prove that after passing to a natural localization of ![]() $\mathrm {VTop}$,
$\mathrm {VTop}$, ![]() $\mathbb {T}_{\mathrm {VTop}}$ becomes isomorphic to
$\mathbb {T}_{\mathrm {VTop}}$ becomes isomorphic to ![]() $\mathbb {T}$. We record the following useful statement.
$\mathbb {T}$. We record the following useful statement.
Lemma A.1 For any symmetric monoidal ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}^\otimes$ (which admits finite limits) and any
$\mathcal {C}^\otimes$ (which admits finite limits) and any ![]() $\infty$-category
$\infty$-category ![]() $K$, there is a natural symmetric monoidal functor
$K$, there is a natural symmetric monoidal functor
where ![]() $\mathrm {Cart}$ is the class of morphisms
$\mathrm {Cart}$ is the class of morphisms ![]() $K\times [1]\to \mathcal {C}$ such that for every functor
$K\times [1]\to \mathcal {C}$ such that for every functor ![]() $[1]\to K$, the composition
$[1]\to K$, the composition ![]() $[1]\times [1]\to \mathcal {C}$ is a Cartesian square in
$[1]\times [1]\to \mathcal {C}$ is a Cartesian square in ![]() $\mathcal {C}$.
$\mathcal {C}$.
Proof. A symmetric monoidal functor (A.2.1) is equivalent to a morphism
This boils down to defining an appropriate functor in ![]() $1\text {-}\mathcal {C}\mathrm {at}^{\Delta ^{\rm op}}$ over
$1\text {-}\mathcal {C}\mathrm {at}^{\Delta ^{\rm op}}$ over ![]() $\mathrm {Seq}_\bullet N(\mathrm {Fin}_*)$
$\mathrm {Seq}_\bullet N(\mathrm {Fin}_*)$
Using (2.2.1) and that
this amounts to defining an appropriate functor
where
 \begin{align*} &\mathrm{Fun}''(([\bullet]\times[\bullet]^{\rm op})^{\geq \mathrm{dgnl}}\times K,\mathcal{C}^{\otimes, \mathrm{Fin}_*^{\rm op}})\\ & :=\mathrm{Fun}(K, \mathrm{Fun}''(([\bullet]\times[\bullet]^{\rm op})^{\geq \mathrm{dgnl}},\mathcal{C}^{\otimes, \mathrm{Fin}_*^{\rm op}}))\underset{\mathrm{Fun}(K\times ([\bullet]\times[\bullet]^{\rm op})^{\geq \mathrm{dgnl}}, N(\mathrm{Fin}^*)^{\rm op})}{\times} \mathrm{Fun}([\bullet]^{\rm op}, N(\mathrm{Fin}^*)^{\rm op}). \end{align*}
\begin{align*} &\mathrm{Fun}''(([\bullet]\times[\bullet]^{\rm op})^{\geq \mathrm{dgnl}}\times K,\mathcal{C}^{\otimes, \mathrm{Fin}_*^{\rm op}})\\ & :=\mathrm{Fun}(K, \mathrm{Fun}''(([\bullet]\times[\bullet]^{\rm op})^{\geq \mathrm{dgnl}},\mathcal{C}^{\otimes, \mathrm{Fin}_*^{\rm op}}))\underset{\mathrm{Fun}(K\times ([\bullet]\times[\bullet]^{\rm op})^{\geq \mathrm{dgnl}}, N(\mathrm{Fin}^*)^{\rm op})}{\times} \mathrm{Fun}([\bullet]^{\rm op}, N(\mathrm{Fin}^*)^{\rm op}). \end{align*}
There is an obvious candidate induced from the natural map
that is doing the obvious evaluation map (after doing the projection ![]() $([\bullet ]\times [\bullet ]^{\rm op})^{\geq \mathrm {dgnl}}\to [\bullet ]$) and projection to the second factor. It is clear that if we use (A.2.3) and restrict to the full subcategory of the second factor of the left-hand side of (A.2.2) defined by the condition that:
$([\bullet ]\times [\bullet ]^{\rm op})^{\geq \mathrm {dgnl}}\to [\bullet ]$) and projection to the second factor. It is clear that if we use (A.2.3) and restrict to the full subcategory of the second factor of the left-hand side of (A.2.2) defined by the condition that:
— for every square
 $\Delta _{hor}^1\times \Delta ^1_K$ in
$\Delta _{hor}^1\times \Delta ^1_K$ in  $\{s\}\times [n]^{\rm op}\times K$, it satisfies the (Obj) condition in § 2.2 with
$\{s\}\times [n]^{\rm op}\times K$, it satisfies the (Obj) condition in § 2.2 with  $\Delta _{vert}^1$ replaced by
$\Delta _{vert}^1$ replaced by  $\Delta ^1_K$;
$\Delta ^1_K$;
then we get the desired functor. However, that full subcategory is exactly given by restricting the horizontal arrows to ![]() $\mathrm {Cart}$.
$\mathrm {Cart}$.
Example A.2 If ![]() $K=\Delta ^1$, then on the object and 1-morphism level,
$K=\Delta ^1$, then on the object and 1-morphism level, ![]() $F_{\Delta ^1, \mathcal {C}}$ sends
$F_{\Delta ^1, \mathcal {C}}$ sends


where the right diagram in (1-Mor) represents a ![]() $\Delta ^1\times \Delta ^1$ in
$\Delta ^1\times \Delta ^1$ in ![]() $\mathrm {Corr}(\mathcal {C})_{\mathsf {all},\mathsf {all}}^{\mathsf {all}}$, with the outer boundary giving the two standard horns in the boundary of
$\mathrm {Corr}(\mathcal {C})_{\mathsf {all},\mathsf {all}}^{\mathsf {all}}$, with the outer boundary giving the two standard horns in the boundary of ![]() $\Delta ^1\times \Delta ^1$. The assignment from
$\Delta ^1\times \Delta ^1$. The assignment from ![]() $F_{\Delta ^1, \mathcal {C}}$ on 2-morphisms is the obvious one.
$F_{\Delta ^1, \mathcal {C}}$ on 2-morphisms is the obvious one.
Recall for an ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\mathbf {C}$ and an object
$\mathbf {C}$ and an object ![]() $c\in \mathbf {C}$, the right-lax coslice
$c\in \mathbf {C}$, the right-lax coslice ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\mathbf {C}^{c//}$ is defined as
$\mathbf {C}^{c//}$ is defined as ![]() $\mathrm {Fun}([1], \mathbf {C})_{\mathrm {R}\text {-}\mathrm {lax}}\underset {\mathrm {Fun}(\{0\},\mathbf {C})}{\times }\{c\}$. If
$\mathrm {Fun}([1], \mathbf {C})_{\mathrm {R}\text {-}\mathrm {lax}}\underset {\mathrm {Fun}(\{0\},\mathbf {C})}{\times }\{c\}$. If ![]() $\mathbf {C}$ is an ordinary
$\mathbf {C}$ is an ordinary ![]() $2$-category, then
$2$-category, then ![]() $\mathbf {C}^{c//}$ is explicitly given by:
$\mathbf {C}^{c//}$ is explicitly given by:
– an object is given by a pair
 $(x, \phi )$:
$(x, \phi )$:  $x\in \mathbf {C}$ and a 1-morphism
$x\in \mathbf {C}$ and a 1-morphism  $\phi : c\to x$;
$\phi : c\to x$;– a 1-morphism from
 $(x, \phi )$ to
$(x, \phi )$ to  $(y, \eta )$ is given by
$(y, \eta )$ is given by  $(f, \alpha )$:
$(f, \alpha )$:

– a 2-morphism from
 $(f,\alpha )$ to
$(f,\alpha )$ to  $(g,\beta )$ is given by a 2-morphism
$(g,\beta )$ is given by a 2-morphism  $\nu : f\to g$ such that
$\nu : f\to g$ such that  $\alpha =\beta \circ ((\nu )\circ \phi )$:
$\alpha =\beta \circ ((\nu )\circ \phi )$:

In the following, for any class of 1-morphisms ![]() $vert$ in
$vert$ in ![]() $\mathcal {C}$ and any
$\mathcal {C}$ and any ![]() $(\infty,1)$-category
$(\infty,1)$-category ![]() $K$, we will denote the class of morphisms
$K$, we will denote the class of morphisms ![]() $\Delta ^1\to \mathrm {Fun}(K,\mathcal {C})$ with
$\Delta ^1\to \mathrm {Fun}(K,\mathcal {C})$ with ![]() $\Delta ^1\times \{k\}, k\in K$ all in
$\Delta ^1\times \{k\}, k\in K$ all in ![]() $vert$ as
$vert$ as ![]() $vert'$ in
$vert'$ in ![]() $\mathrm {Fun}(K, \mathcal {C})$. If
$\mathrm {Fun}(K, \mathcal {C})$. If ![]() $\mathcal {C}=\mathrm {S}_{\mathrm {LCH}}, \mathrm {Top}, \mathcal {V}\mathcal {S}\mathrm {pc}$, then we let
$\mathcal {C}=\mathrm {S}_{\mathrm {LCH}}, \mathrm {Top}, \mathcal {V}\mathcal {S}\mathrm {pc}$, then we let ![]() $vert'$ be the class of morphisms in
$vert'$ be the class of morphisms in ![]() $\mathrm {V}\mathrm {S}_{\mathrm {LCH}}, \mathrm {VTop}, \mathcal {V}\mathcal {S}\mathrm {pc}$, respectively, whose image under the projection to
$\mathrm {V}\mathrm {S}_{\mathrm {LCH}}, \mathrm {VTop}, \mathcal {V}\mathcal {S}\mathrm {pc}$, respectively, whose image under the projection to ![]() $\mathcal {C}$ are in
$\mathcal {C}$ are in ![]() $vert$. Assume the classes of morphisms
$vert$. Assume the classes of morphisms ![]() $(vert, horiz=\mathsf {all}, adm=vert)$ satisfy [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 1.1.1] and
$(vert, horiz=\mathsf {all}, adm=vert)$ satisfy [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 1.1.1] and ![]() $vert$ is closed under the tensor product functor on
$vert$ is closed under the tensor product functor on ![]() $\mathcal {C}$. Then it is clear from Lemma A.1 that (A.2.1) restricts to a symmetric monoidal functor (which by some abuse of notations, we still denote by
$\mathcal {C}$. Then it is clear from Lemma A.1 that (A.2.1) restricts to a symmetric monoidal functor (which by some abuse of notations, we still denote by ![]() $F_{K,\mathcal {C}}$)
$F_{K,\mathcal {C}}$)
Lemma A.3 For any ![]() $(\infty,1)$-category
$(\infty,1)$-category ![]() $\mathcal {C}$ which admits finite limits and given classes of morphisms
$\mathcal {C}$ which admits finite limits and given classes of morphisms ![]() $(vert, horiz=\mathsf {all}, adm=vert)$ satisfying [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 1.1.1] and
$(vert, horiz=\mathsf {all}, adm=vert)$ satisfying [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 1.1.1] and ![]() $vert$ is closed under taking products, there is a natural symmetric monoidal
$vert$ is closed under taking products, there is a natural symmetric monoidal ![]() $(\infty,2)$-functor
$(\infty,2)$-functor
with respect to the symmetric monoidal structure inherited from ![]() $\mathcal {C}^\times$, such that:
$\mathcal {C}^\times$, such that:
– on the object level, every object
 $(f: x\to y)\in \mathrm {Fun}(\Delta ^1, \mathcal {C})$ is sent to
$(f: x\to y)\in \mathrm {Fun}(\Delta ^1, \mathcal {C})$ is sent to

– any 1-morphism in
 $\mathrm {Corr}(\mathrm {Fun}(\Delta ^1, \mathcal {C}))_{vert, \mathrm {Cart}}^{vert}$ given by
is sent to
$\mathrm {Corr}(\mathrm {Fun}(\Delta ^1, \mathcal {C}))_{vert, \mathrm {Cart}}^{vert}$ given by
is sent to (A.2.5)where (1) the lower right half of the rectangle in (A.2.5) represents a
(A.2.5)where (1) the lower right half of the rectangle in (A.2.5) represents a
 $\Delta ^2$ in
$\Delta ^2$ in  $\mathrm {Corr}(\mathcal {C})_{vert, \mathsf {all}}^{vert}$ with vertices
$\mathrm {Corr}(\mathcal {C})_{vert, \mathsf {all}}^{vert}$ with vertices  $0,1,2$ going to
$0,1,2$ going to  $\star, y_{00}, y_{11}$, respectively, and (2) the thickened upper left arrow represents a 2-morphism in
$\star, y_{00}, y_{11}$, respectively, and (2) the thickened upper left arrow represents a 2-morphism in  ${\mathcal {M} \text{aps}}_{\mathrm {Corr}(\mathcal {C})_{vert, \mathsf {all}}^{vert}}(\star, y_{11})$;
${\mathcal {M} \text{aps}}_{\mathrm {Corr}(\mathcal {C})_{vert, \mathsf {all}}^{vert}}(\star, y_{11})$;– for any 2-morphism in
 $\mathrm {Corr}(\mathrm {Fun}(\Delta ^1, \mathcal {C}))_{vert', \mathrm {Cart}}^{vert'}$, given by a commutative diagram
we assign the following commutative diagram that represents a 2-morphism in
$\mathrm {Corr}(\mathrm {Fun}(\Delta ^1, \mathcal {C}))_{vert', \mathrm {Cart}}^{vert'}$, given by a commutative diagram
we assign the following commutative diagram that represents a 2-morphism in
 $(\mathrm {Corr}(\mathcal {C})_{vert, \mathsf {all}}^{vert})^{\star / / }$.
$(\mathrm {Corr}(\mathcal {C})_{vert, \mathsf {all}}^{vert})^{\star / / }$.

Proof. We will define a symmetric monoidal functor
below, then we let

where
is the natural (symmetric monoidal) functor induced from ![]() $\Delta ^{\{0\}}\hookrightarrow \Delta ^{\{0,1\}}$, and
$\Delta ^{\{0\}}\hookrightarrow \Delta ^{\{0,1\}}$, and ![]() $\mu ^{\mathrm {R}\text {-}\mathrm {lax}}_{1,1}$ is the composition functor. It is clear that
$\mu ^{\mathrm {R}\text {-}\mathrm {lax}}_{1,1}$ is the composition functor. It is clear that ![]() $F_{\Delta ^1, \mathcal {C}}^{\star //}$ factors through
$F_{\Delta ^1, \mathcal {C}}^{\star //}$ factors through ![]() $(\mathrm {Corr}(\mathcal {C})_{\mathsf {all}, \mathsf {all}}^{vert})^{\star / / }$ (so it goes to the correct target).
$(\mathrm {Corr}(\mathcal {C})_{\mathsf {all}, \mathsf {all}}^{vert})^{\star / / }$ (so it goes to the correct target).
We will define ![]() $(F_\mathcal {C}^{\star //})_n: \mathrm {Seq}_n(\mathrm {Corr}(\mathcal {C})_{vert, \mathsf {all}}^{vert})\to \mathrm {Seq}_n((\mathrm {Corr}(\mathcal {C})_{\mathsf {all}, \mathsf {all}}^{vert})^{\star / / })$ as follows. For any
$(F_\mathcal {C}^{\star //})_n: \mathrm {Seq}_n(\mathrm {Corr}(\mathcal {C})_{vert, \mathsf {all}}^{vert})\to \mathrm {Seq}_n((\mathrm {Corr}(\mathcal {C})_{\mathsf {all}, \mathsf {all}}^{vert})^{\star / / })$ as follows. For any ![]() $n$-simplex in
$n$-simplex in ![]() $\mathrm {Corr}(\mathcal {C})_{vert, \mathsf {all}}^{vert}$ represented by a functor
$\mathrm {Corr}(\mathcal {C})_{vert, \mathsf {all}}^{vert}$ represented by a functor ![]() $C: ([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}\to \mathcal {C}$, we can explicitly write down the functor
$C: ([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}\to \mathcal {C}$, we can explicitly write down the functor ![]() $[n]{\bigcirc{\kern-6pt \star}}[1]\to \mathrm {Corr}(\mathcal {C})_{\mathsf {all},\mathsf {all}}^{vert}$ representing
$[n]{\bigcirc{\kern-6pt \star}}[1]\to \mathrm {Corr}(\mathcal {C})_{\mathsf {all},\mathsf {all}}^{vert}$ representing ![]() $(F_{\mathcal {C}}^{\star //})_n(C)$. Namely, for any
$(F_{\mathcal {C}}^{\star //})_n(C)$. Namely, for any ![]() $(s,t;u)\in \mathrm {Seq}_k([n]{\bigcirc{\kern-6pt \star}}[1])$:
$(s,t;u)\in \mathrm {Seq}_k([n]{\bigcirc{\kern-6pt \star}}[1])$:

where arrow means ![]() $\leq$, the corresponding diagram in
$\leq$, the corresponding diagram in ![]() $\mathrm {Seq}_k(\mathrm {Corr}(\mathcal {C})_{\mathsf {all},\mathsf {all}}^{vert})$, denoted by
$\mathrm {Seq}_k(\mathrm {Corr}(\mathcal {C})_{\mathsf {all},\mathsf {all}}^{vert})$, denoted by ![]() $(V_{i,j})_{0\leq i\leq j\leq k}$, has
$(V_{i,j})_{0\leq i\leq j\leq k}$, has
 \begin{align*} & V_{i,j}=\star,\
0\leq i\leq j\leq \mu-1,\\ & V_{i, \mu+j}=C_{u,
t_{\mu+j}},\ 0\leq i\leq \mu-1, 0\leq j\leq
n-\mu,\\ & V_{\mu+i, \mu+j}=C_{t_{\mu+i},
t_{\mu+j}},\ 0\leq i\leq j\leq n-\mu, \\
\end{align*}
\begin{align*} & V_{i,j}=\star,\
0\leq i\leq j\leq \mu-1,\\ & V_{i, \mu+j}=C_{u,
t_{\mu+j}},\ 0\leq i\leq \mu-1, 0\leq j\leq
n-\mu,\\ & V_{\mu+i, \mu+j}=C_{t_{\mu+i},
t_{\mu+j}},\ 0\leq i\leq j\leq n-\mu, \\
\end{align*}
and the morphisms between ![]() $V_{i,j}$ are determined by
$V_{i,j}$ are determined by ![]() $C$ in the obvious way. For any
$C$ in the obvious way. For any ![]() $(s,t;u)\to (s,t;u')$, the corresponding 1-morphism in
$(s,t;u)\to (s,t;u')$, the corresponding 1-morphism in ![]() $\mathrm {Seq}_k(\mathrm {Corr}(\mathcal {C})_{\mathsf {all},\mathsf {all}}^{vert})$ is also the obvious one. For any
$\mathrm {Seq}_k(\mathrm {Corr}(\mathcal {C})_{\mathsf {all},\mathsf {all}}^{vert})$ is also the obvious one. For any ![]() $m$-simplex in
$m$-simplex in ![]() $\mathrm {Seq}_n(\mathrm {Corr}(\mathcal {C}))_{vert, \mathsf {all}}^{vert})$, we get a natural functor
$\mathrm {Seq}_n(\mathrm {Corr}(\mathcal {C}))_{vert, \mathsf {all}}^{vert})$, we get a natural functor
which gives an element in
These assemble to be a well-defined functor
where ![]() $\mathrm {Sq}_{m,n}^{\tilde {}}:=\mathrm {Seq}_m\mathrm {Seq}_n$ (cf. [Reference Gaitsgory and RozenblyumGR17, Chapter 10, 2.6]). Clearly, everything is functorial in
$\mathrm {Sq}_{m,n}^{\tilde {}}:=\mathrm {Seq}_m\mathrm {Seq}_n$ (cf. [Reference Gaitsgory and RozenblyumGR17, Chapter 10, 2.6]). Clearly, everything is functorial in ![]() $m,n$, hence this gives the full description of
$m,n$, hence this gives the full description of ![]() $F_\mathcal {C}^{\star //}$.
$F_\mathcal {C}^{\star //}$.
The assertion about the symmetric monoidal structure on ![]() $F_\mathcal {C}^{\star //}$ can be obtained similarly by upgrading
$F_\mathcal {C}^{\star //}$ can be obtained similarly by upgrading ![]() $(F_\mathcal {C}^{\star //})_n$ to
$(F_\mathcal {C}^{\star //})_n$ to
over ![]() $\mathrm {Seq}_n\big (N(\mathrm {Fin}_*)\big )$. We omit the details since the argument is similar to many arguments explicitly carried out in § 2.4.
$\mathrm {Seq}_n\big (N(\mathrm {Fin}_*)\big )$. We omit the details since the argument is similar to many arguments explicitly carried out in § 2.4.
Proposition A.4 Let ![]() $\mathcal {C}$ be an ordinary 1-category which admits finite limits. Let
$\mathcal {C}$ be an ordinary 1-category which admits finite limits. Let ![]() $W^\bullet \to D^\bullet$ be an
$W^\bullet \to D^\bullet$ be an ![]() $N(\mathrm {Fin}_*)$-object in
$N(\mathrm {Fin}_*)$-object in ![]() $\mathrm {Fun}(\Delta ^1, \mathcal {C})$ that satisfies the conditions in Theorem 2.13 as a correspondence
$\mathrm {Fun}(\Delta ^1, \mathcal {C})$ that satisfies the conditions in Theorem 2.13 as a correspondence ![]() $D^\bullet \leftarrow W^\bullet \to W^\bullet$. Then:
$D^\bullet \leftarrow W^\bullet \to W^\bullet$. Then:
(i)
 $W^\bullet \to D^\bullet$ represents a commutative algebra object in
$W^\bullet \to D^\bullet$ represents a commutative algebra object in  $\mathbf {Corr}(\mathrm {Fun}(\Delta ^1, \mathcal {C}))$;
$\mathbf {Corr}(\mathrm {Fun}(\Delta ^1, \mathcal {C}))$;(ii) the right-lax homomorphism determined by the correspondence
 $D^\bullet \leftarrow W^\bullet \to \star ^\bullet$ (using Theorem 2.13) is isomorphic to the image of the commutative algebra object in part (i) under
$D^\bullet \leftarrow W^\bullet \to \star ^\bullet$ (using Theorem 2.13) is isomorphic to the image of the commutative algebra object in part (i) under  $F_{\Delta ^1, \mathcal {C}}^{\star //}$ (for
$F_{\Delta ^1, \mathcal {C}}^{\star //}$ (for  $vert=\mathsf {all}$).
$vert=\mathsf {all}$).
Proof. (i) This follows directly from Theorem 2.13.
(ii) It reduces to the case when ![]() $W^\bullet =D^\bullet$ (and the morphism is the identity). Since
$W^\bullet =D^\bullet$ (and the morphism is the identity). Since ![]() $\mathcal {C}$ is assumed to be ordinary, one can check this directly using the proof of Theorem 2.8 and Theorem 2.13. We sketch the steps below.
$\mathcal {C}$ is assumed to be ordinary, one can check this directly using the proof of Theorem 2.8 and Theorem 2.13. We sketch the steps below.
Step 1. The data of the commutative algebra ![]() $W\in \mathrm {Corr}(\mathcal {C})_{vert, \mathsf {all}}^{vert}$ that is determined by
$W\in \mathrm {Corr}(\mathcal {C})_{vert, \mathsf {all}}^{vert}$ that is determined by ![]() $W^\bullet$ is exactly encoded by the ‘multiplication rule’: for any
$W^\bullet$ is exactly encoded by the ‘multiplication rule’: for any ![]() $\alpha \in \mathrm {Seq}_n(N(\mathrm {Fin}_*))$, we get a functor
$\alpha \in \mathrm {Seq}_n(N(\mathrm {Fin}_*))$, we get a functor ![]() $([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}\times _{N(\mathrm {Fin}_*)^{\rm op}}T^{\mathrm {Comm}}\to \mathcal {C}$, and by taking the right Kan extension along the projection
$([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}\times _{N(\mathrm {Fin}_*)^{\rm op}}T^{\mathrm {Comm}}\to \mathcal {C}$, and by taking the right Kan extension along the projection ![]() $([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}\times _{N(\mathrm {Fin}_*)^{\rm op}}T^{\mathrm {Comm}}\to ([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}$, we get a diagram
$([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}\times _{N(\mathrm {Fin}_*)^{\rm op}}T^{\mathrm {Comm}}\to ([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}$, we get a diagram ![]() $([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}\to \mathcal {C}$ that encodes the ‘multiplication rule’ of
$([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}\to \mathcal {C}$ that encodes the ‘multiplication rule’ of ![]() $W$ with respect to
$W$ with respect to ![]() $\alpha$.
$\alpha$.
Under ![]() $F_{\mathcal {C}}^{\star //}$, the above diagram as an
$F_{\mathcal {C}}^{\star //}$, the above diagram as an ![]() $n$-simplex in
$n$-simplex in ![]() $\mathrm {Corr}(\mathcal {C})_{vert, \mathsf {all}}^{vert}$ gives a functor
$\mathrm {Corr}(\mathcal {C})_{vert, \mathsf {all}}^{vert}$ gives a functor ![]() $[n]{\bigcirc{\kern-6pt \star}} [1]\to \mathrm {Corr}(\mathcal {C})_{\mathsf {all}, \mathsf {all}}^{vert}$, where
$[n]{\bigcirc{\kern-6pt \star}} [1]\to \mathrm {Corr}(\mathcal {C})_{\mathsf {all}, \mathsf {all}}^{vert}$, where ![]() $[n]\times \{0\}$ is sent to
$[n]\times \{0\}$ is sent to ![]() $\star$ and
$\star$ and ![]() $[n]\times \{1\}$ is sent to the given
$[n]\times \{1\}$ is sent to the given ![]() $n$-simplex. This functor is explicitly given in the proof of Lemma A.3.
$n$-simplex. This functor is explicitly given in the proof of Lemma A.3.
Step 2. On the other hand, unwinding the definition, an element in ![]() $\mathrm {CAlg}((\mathrm {Corr}(\mathcal {C})_{\mathsf {all}, \mathsf {all}}^{vert})^{\star //})$ is equivalent to a right-lax homomorphism from
$\mathrm {CAlg}((\mathrm {Corr}(\mathcal {C})_{\mathsf {all}, \mathsf {all}}^{vert})^{\star //})$ is equivalent to a right-lax homomorphism from ![]() $\star$ (with the trivial commutative algebra structure) to a commutative algebra in
$\star$ (with the trivial commutative algebra structure) to a commutative algebra in ![]() $\mathrm {Corr}(\mathcal {C})_{\mathsf {all}, \mathsf {all}}^{vert}$. This is again encoded by the family of functors
$\mathrm {Corr}(\mathcal {C})_{\mathsf {all}, \mathsf {all}}^{vert}$. This is again encoded by the family of functors ![]() $[n]{\bigcirc{\kern-6pt \star}}[1]\to \mathrm {Corr}(\mathcal {C})_{\mathsf {all}, \mathsf {all}}^{vert}$ associated to
$[n]{\bigcirc{\kern-6pt \star}}[1]\to \mathrm {Corr}(\mathcal {C})_{\mathsf {all}, \mathsf {all}}^{vert}$ associated to ![]() $\alpha \in \mathrm {Seq}_n(N(\mathrm {Fin}_*))$. Such functors associated to
$\alpha \in \mathrm {Seq}_n(N(\mathrm {Fin}_*))$. Such functors associated to ![]() $W^\bullet \overset {id}{\leftarrow }W^\bullet \to \star ^\bullet$ from Theorem 2.13 are also explicitly given in the proof of that theorem. We just need to compare these functors with those from Step 1. Again, using that all 1- and 2-morphisms are discrete, and both assignments to any
$W^\bullet \overset {id}{\leftarrow }W^\bullet \to \star ^\bullet$ from Theorem 2.13 are also explicitly given in the proof of that theorem. We just need to compare these functors with those from Step 1. Again, using that all 1- and 2-morphisms are discrete, and both assignments to any ![]() $\alpha \in \mathrm {Seq}_n(N(\mathrm {Fin}_*))$ are identical, the proof is complete.
$\alpha \in \mathrm {Seq}_n(N(\mathrm {Fin}_*))$ are identical, the proof is complete.
Let ![]() $\pi _{X,pt}: X\to pt$ be the map to the terminal object in
$\pi _{X,pt}: X\to pt$ be the map to the terminal object in ![]() $\mathrm {S}_{\mathrm {LCH}}$.
$\mathrm {S}_{\mathrm {LCH}}$.
Corollary A.5 There is a natural symmetric monoidal functorFootnote 9
 \begin{align*} \mathrm{ShvSp}^!_{*;\mathrm{Sp} //}: \mathrm{Corr}(\mathrm{V}\mathrm{S}_{\mathrm{LCH}})_{\mathsf{prop}', \mathsf{all}}^{\mathsf{prop}'}&\to (\mathbf{Pr}_{\mathrm{st}}^{\mathrm{R}})^{\mathrm{Sp}/ /}\\ (p_V: V\to X)&\mapsto (\mathrm{Shv}(X;\mathrm{Sp})\ni (p_V)_*\varpi_{V}) \end{align*}
\begin{align*} \mathrm{ShvSp}^!_{*;\mathrm{Sp} //}: \mathrm{Corr}(\mathrm{V}\mathrm{S}_{\mathrm{LCH}})_{\mathsf{prop}', \mathsf{all}}^{\mathsf{prop}'}&\to (\mathbf{Pr}_{\mathrm{st}}^{\mathrm{R}})^{\mathrm{Sp}/ /}\\ (p_V: V\to X)&\mapsto (\mathrm{Shv}(X;\mathrm{Sp})\ni (p_V)_*\varpi_{V}) \end{align*}
that sends a correspondence

to

where ![]() $\alpha : g_*f^!(p_{00})_*\pi _{V_{00}, pt}^!\cong (p_{11})_*\tilde {g}_!\tilde {g}^!\pi _{V_{11},pt}^!\to (p_{11})_*\pi _{V_{11}, pt}^!$ is induced from the adjunction from
$\alpha : g_*f^!(p_{00})_*\pi _{V_{00}, pt}^!\cong (p_{11})_*\tilde {g}_!\tilde {g}^!\pi _{V_{11},pt}^!\to (p_{11})_*\pi _{V_{11}, pt}^!$ is induced from the adjunction from ![]() $\tilde {g}_!\tilde {g}^!\to id_{\mathrm {Shv}(V_{11};\mathrm {Sp})}$.
$\tilde {g}_!\tilde {g}^!\to id_{\mathrm {Shv}(V_{11};\mathrm {Sp})}$.
Proof. Using Lemma A.3 and ![]() $\mathrm {ShvSp}_*^!$, the sought-for functor is defined as the composition
$\mathrm {ShvSp}_*^!$, the sought-for functor is defined as the composition
Let ![]() $\mathbb {T}_{\mathrm {Shv}}^!: \mathrm {V}\mathrm {S}_{\mathrm {LCH}}^{\rm op}\to (\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}})^{\mathrm {Sp}//}$ be the restriction of
$\mathbb {T}_{\mathrm {Shv}}^!: \mathrm {V}\mathrm {S}_{\mathrm {LCH}}^{\rm op}\to (\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}})^{\mathrm {Sp}//}$ be the restriction of ![]() $\mathrm {ShvSp}^!_{*;\mathrm {Sp} //}$ to the 1-full subcategory
$\mathrm {ShvSp}^!_{*;\mathrm {Sp} //}$ to the 1-full subcategory ![]() $\mathrm {V}\mathrm {S}_{\mathrm {LCH}}^{\rm op}$. Since any morphism in
$\mathrm {V}\mathrm {S}_{\mathrm {LCH}}^{\rm op}$. Since any morphism in ![]() $\mathrm {V}\mathrm {S}_{\mathrm {LCH}}^{\rm op}$ is a correspondence (A.2.6) with
$\mathrm {V}\mathrm {S}_{\mathrm {LCH}}^{\rm op}$ is a correspondence (A.2.6) with ![]() $V_{01}=V_{11}$ and
$V_{01}=V_{11}$ and ![]() $X_{01}=X_{11}$ (and
$X_{01}=X_{11}$ (and ![]() $g$ and
$g$ and ![]() $\tilde {g}$ the identity morphisms),
$\tilde {g}$ the identity morphisms), ![]() $\mathbb {T}_{\mathrm {Shv}}^!$ factors through the
$\mathbb {T}_{\mathrm {Shv}}^!$ factors through the ![]() $(\infty,1)$-category
$(\infty,1)$-category ![]() $(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {R}})^{\mathrm {Sp}/}$. Recall the right Beck–Chevalley condition defined in [Reference Gaitsgory and RozenblyumGR17, Chapter 7, Definition 3.1.5].
$(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {R}})^{\mathrm {Sp}/}$. Recall the right Beck–Chevalley condition defined in [Reference Gaitsgory and RozenblyumGR17, Chapter 7, Definition 3.1.5].
Corollary A.6 The functor ![]() $\mathbb {T}_{\mathrm {Shv}}^!$ satisfies the right Beck–Chevalley condition with respect to
$\mathbb {T}_{\mathrm {Shv}}^!$ satisfies the right Beck–Chevalley condition with respect to ![]() $\mathsf {prop}'$. In particular, for any
$\mathsf {prop}'$. In particular, for any ![]() $(f, \varphi ): (V, X)\to (V',Y)$ with
$(f, \varphi ): (V, X)\to (V',Y)$ with ![]() $f$ proper,
$f$ proper, ![]() $\mathbb {T}_{\mathrm {Shv}}^!(f,\varphi )$ in
$\mathbb {T}_{\mathrm {Shv}}^!(f,\varphi )$ in ![]() $(\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}})^{\mathrm {Sp}/ /}$ is left adjointable.
$(\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}})^{\mathrm {Sp}/ /}$ is left adjointable.
Proof. This follows immediately from the universal property of functors out of correspondences, established in [Reference Gaitsgory and RozenblyumGR17, Chapter 7, Theorem 3.2.2 (b)].
Definition A.7 [Reference Gaitsgory and RozenblyumGR17, Chapter 11, 1.2.2] We say an ![]() $(\infty,2)$-functor
$(\infty,2)$-functor ![]() $F: \mathbf {C}\to \mathbf {D}$ is a 1-Cartesian (respectively, 1-coCartesian) fibration if the following hold:
$F: \mathbf {C}\to \mathbf {D}$ is a 1-Cartesian (respectively, 1-coCartesian) fibration if the following hold:
(1) the induced functor
 $\mathbf {C}^{1\text {-}\mathcal {C}\mathrm {at}}\to \mathbf {D}^{1\text {-}\mathcal {C}\mathrm {at}}$ is a Cartesian (respectively, coCartesian) fibration;
$\mathbf {C}^{1\text {-}\mathcal {C}\mathrm {at}}\to \mathbf {D}^{1\text {-}\mathcal {C}\mathrm {at}}$ is a Cartesian (respectively, coCartesian) fibration;(2) for every
 $c',c\in \mathbf {C}$, the functor
is a coCartesian (respectively, Cartesian) fibration in spaces.
$c',c\in \mathbf {C}$, the functor
is a coCartesian (respectively, Cartesian) fibration in spaces. \[ {\mathcal{M}\text{aps}}_{\mathbf{C}}(c',c)\to {\mathcal{M}\text{aps}}_{\mathbf{D}}(F(c'), F(c)) \]
\[ {\mathcal{M}\text{aps}}_{\mathbf{C}}(c',c)\to {\mathcal{M}\text{aps}}_{\mathbf{D}}(F(c'), F(c)) \]
By [Reference Gaitsgory and RozenblyumGR17, Chapter 11, Lemma 1.2.5], ![]() $F: \mathbf {C}\to \mathbf {D}$ is a 1-Cartesian (respectively, 1-coCartesian) fibration if and only if
$F: \mathbf {C}\to \mathbf {D}$ is a 1-Cartesian (respectively, 1-coCartesian) fibration if and only if ![]() $F$ is a 2-Cartesian (respectively, 2-coCartesian) fibration whose fiber over any
$F$ is a 2-Cartesian (respectively, 2-coCartesian) fibration whose fiber over any ![]() $d\in \mathbf {D}$ is an
$d\in \mathbf {D}$ is an ![]() $(\infty,1)$-category.
$(\infty,1)$-category.
Lemma A.8 For any ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\mathbf {C}$ and any
$\mathbf {C}$ and any ![]() $c\in \mathbf {C}$,
$c\in \mathbf {C}$, ![]() $\mathbf {C}^{c/ / }\to \mathbf {C}$ is a 1-coCartesian fibration.
$\mathbf {C}^{c/ / }\to \mathbf {C}$ is a 1-coCartesian fibration.
Proof. This is the dual version of [Reference Gaitsgory and RozenblyumGR17, Chapter 11, Lemma 5.1.4]. Indeed, we have
and it is proved in [Reference Gaitsgory and RozenblyumGR17] that ![]() $(\mathbf {C}^{1\& 2\text {-}\mathrm {op}})^{/ / c}\to \mathbf {C}^{1\& 2\text {-}\mathrm {op}}$ is a 1-Cartesian fibration.
$(\mathbf {C}^{1\& 2\text {-}\mathrm {op}})^{/ / c}\to \mathbf {C}^{1\& 2\text {-}\mathrm {op}}$ is a 1-Cartesian fibration.
Remark A.9 Assume ![]() $\mathbf {C}$ is an ordinary 2-category and
$\mathbf {C}$ is an ordinary 2-category and ![]() $c\in \mathbf {C}$. Let
$c\in \mathbf {C}$. Let ![]() $(\phi :c\to a)\in \mathbf {C}^{c//}$ and
$(\phi :c\to a)\in \mathbf {C}^{c//}$ and ![]() $L: a \rightleftarrows b: R$ be an adjoint pair in
$L: a \rightleftarrows b: R$ be an adjoint pair in ![]() $\mathbf {C}$ with unit and co-unit given by
$\mathbf {C}$ with unit and co-unit given by ![]() $\varepsilon : id_a\to RL$ and
$\varepsilon : id_a\to RL$ and ![]() $\vartheta : LR\to id_b$, respectively. Let
$\vartheta : LR\to id_b$, respectively. Let ![]() $\widetilde {R}=(R, id_{R\circ \phi }): \phi \to R\circ \phi$ be a 1-coCartesian (equivalently 2-coCartesian) 1-morphism in
$\widetilde {R}=(R, id_{R\circ \phi }): \phi \to R\circ \phi$ be a 1-coCartesian (equivalently 2-coCartesian) 1-morphism in ![]() $\mathbf {C}^{c//}$ over
$\mathbf {C}^{c//}$ over ![]() $R$. Then it is easy to see that
$R$. Then it is easy to see that ![]() $\widetilde {R}$ has a left adjoint
$\widetilde {R}$ has a left adjoint ![]() $\widetilde {L}$ represented by
$\widetilde {L}$ represented by ![]() $(L, (\vartheta )\circ \phi ): R\circ \phi \to \phi$.
$(L, (\vartheta )\circ \phi ): R\circ \phi \to \phi$.
As explained in [Reference Gaitsgory and RozenblyumGR17, Chapter 12, § 1.1], the notion of adjoint pairs in an ![]() $(\infty, 2)$-category only depends on the underlying ordinary 2-category (cf. [Reference Gaitsgory and RozenblyumGR17, Chapter 10, 2.2.5] for the notion of
$(\infty, 2)$-category only depends on the underlying ordinary 2-category (cf. [Reference Gaitsgory and RozenblyumGR17, Chapter 10, 2.2.5] for the notion of ![]() $(-)^{\mathrm {ordn}}$). However, we note that for an
$(-)^{\mathrm {ordn}}$). However, we note that for an ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\mathbf {C}$,
$\mathbf {C}$,
in general, since a 2-morphism (always invertible) in a fiber of ![]() $(\mathbf {C}^{c//})^{\mathrm {ordn}}\to \mathbf {C}^{\mathrm {ordn}}$ might involve a 3-morphism in
$(\mathbf {C}^{c//})^{\mathrm {ordn}}\to \mathbf {C}^{\mathrm {ordn}}$ might involve a 3-morphism in ![]() $\mathbf {C}$ that is not isomorphic to the identity 3-morphism. Hence, it is not clear whether the above fact for ordinary 2-categories holds for an arbitrary
$\mathbf {C}$ that is not isomorphic to the identity 3-morphism. Hence, it is not clear whether the above fact for ordinary 2-categories holds for an arbitrary ![]() $(\infty,2)$-category. This means Corollary A.6 does not follow directly from the above observation for ordinary 2-categories. On the other hand, it is clear that for any
$(\infty,2)$-category. This means Corollary A.6 does not follow directly from the above observation for ordinary 2-categories. On the other hand, it is clear that for any ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\mathbf {C}$, if
$\mathbf {C}$, if ![]() $\widetilde {R}$ as above admits a left adjoint
$\widetilde {R}$ as above admits a left adjoint ![]() $\widetilde {L}$, then
$\widetilde {L}$, then ![]() $\widetilde {L}$ must be represented by
$\widetilde {L}$ must be represented by ![]() $(L, (\vartheta )\circ \phi ): R\circ \phi \to \phi$ (up to isomorphisms), as if
$(L, (\vartheta )\circ \phi ): R\circ \phi \to \phi$ (up to isomorphisms), as if ![]() $\widetilde {L}$ were different from
$\widetilde {L}$ were different from ![]() $(L, (\vartheta )\circ \phi ): R\circ \phi \to \phi$, then passing from
$(L, (\vartheta )\circ \phi ): R\circ \phi \to \phi$, then passing from ![]() $\mathbf {C}$ to
$\mathbf {C}$ to ![]() $\mathbf {C}^{\mathrm {ordn}}$ would give a different left adjoint to
$\mathbf {C}^{\mathrm {ordn}}$ would give a different left adjoint to ![]() $\widetilde {R}$ considered now in
$\widetilde {R}$ considered now in ![]() $(\mathbf {C}^{\mathrm {ordn}})^{c//}$, which is absurd.
$(\mathbf {C}^{\mathrm {ordn}})^{c//}$, which is absurd.
Let ![]() $\mathsf {prop}\mathsf {fib}=\mathsf {fib}\cap \mathsf {prop}$ be the class of morphisms of proper locally trivial fibrations in
$\mathsf {prop}\mathsf {fib}=\mathsf {fib}\cap \mathsf {prop}$ be the class of morphisms of proper locally trivial fibrations in ![]() $\mathrm {Top}$, and let
$\mathrm {Top}$, and let ![]() $\mathsf {prop}\mathsf {fib}'$ be the preimage of
$\mathsf {prop}\mathsf {fib}'$ be the preimage of ![]() $\mathsf {prop}\mathsf {fib}$ under
$\mathsf {prop}\mathsf {fib}$ under ![]() $\mathrm {VTop}\to \mathrm {Top}$. With some abuse of notation, we also use
$\mathrm {VTop}\to \mathrm {Top}$. With some abuse of notation, we also use ![]() $\mathsf {propfib}$ and
$\mathsf {propfib}$ and ![]() $\mathsf {propfib}'$ to denote the similarly defined classes of morphisms in
$\mathsf {propfib}'$ to denote the similarly defined classes of morphisms in ![]() $\mathrm {S}_{\mathrm {LCH}}$ and
$\mathrm {S}_{\mathrm {LCH}}$ and ![]() $\mathrm {V}\mathrm {S}_{\mathrm {LCH}}$, respectively.
$\mathrm {V}\mathrm {S}_{\mathrm {LCH}}$, respectively.
Lemma A.10 The restriction of ![]() $\mathrm {ShvSp}^!_{*;\mathrm {Sp} //}$ to
$\mathrm {ShvSp}^!_{*;\mathrm {Sp} //}$ to ![]() $\mathrm {Corr}(\mathrm {V}\mathrm {S}_{\mathrm {LCH}})_{\mathsf {propfib}, \mathsf {all}}$ induces a natural symmetric monoidal functor
$\mathrm {Corr}(\mathrm {V}\mathrm {S}_{\mathrm {LCH}})_{\mathsf {propfib}, \mathsf {all}}$ induces a natural symmetric monoidal functor
 \begin{align*} \mathrm{Loc}^!_{!;\mathrm{Sp} //}: \mathrm{Corr}(\mathrm{V}\mathrm{S}_{\mathrm{LCH}})_{\mathsf{propfib}', \mathsf{all}}&\to (\mathbf{Pr}_{\mathrm{st}}^{\mathrm{L}})^{\mathrm{Sp}/ /}\\ (p_V: V\to X)&\mapsto \mathrm{Loc}(X;\mathrm{Sp})\ni (p_V)_*\varpi_{V}. \end{align*}
\begin{align*} \mathrm{Loc}^!_{!;\mathrm{Sp} //}: \mathrm{Corr}(\mathrm{V}\mathrm{S}_{\mathrm{LCH}})_{\mathsf{propfib}', \mathsf{all}}&\to (\mathbf{Pr}_{\mathrm{st}}^{\mathrm{L}})^{\mathrm{Sp}/ /}\\ (p_V: V\to X)&\mapsto \mathrm{Loc}(X;\mathrm{Sp})\ni (p_V)_*\varpi_{V}. \end{align*}
Proof. For any morphism ![]() $(f, \tilde {f})$ in
$(f, \tilde {f})$ in ![]() $(\mathrm {V}\mathrm {S}_{\mathrm {LCH}})_{\mathsf {propfib}'}$ as in (A.2.6), its corresponding 1-morphism under
$(\mathrm {V}\mathrm {S}_{\mathrm {LCH}})_{\mathsf {propfib}'}$ as in (A.2.6), its corresponding 1-morphism under ![]() $\mathrm {ShvSp}^!_{*;\mathrm {Sp}//}$ in
$\mathrm {ShvSp}^!_{*;\mathrm {Sp}//}$ in ![]() $(\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}})^{\mathrm {Sp}//}$ is shown in (A.2.7) with
$(\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}})^{\mathrm {Sp}//}$ is shown in (A.2.7) with ![]() $g=id_{X_{11}}$ and
$g=id_{X_{11}}$ and ![]() $\tilde {g}=id_{V_{11}}$, and its left adjoint is (A.2.7) with
$\tilde {g}=id_{V_{11}}$, and its left adjoint is (A.2.7) with ![]() $g=f, \tilde {g}=\tilde {f}$, and
$g=f, \tilde {g}=\tilde {f}$, and ![]() $f, \tilde {f}$ replaced by the identity morphisms.
$f, \tilde {f}$ replaced by the identity morphisms.
Then the lemma follows from the fact that for any ![]() $f: X\to Y$ in
$f: X\to Y$ in ![]() $\mathsf {propfib}$, the restriction of
$\mathsf {propfib}$, the restriction of ![]() $f_*: \mathrm {Shv}(X;\mathrm {Sp})\to \mathrm {Shv}(Y;\mathrm {Sp})$ to local systems give
$f_*: \mathrm {Shv}(X;\mathrm {Sp})\to \mathrm {Shv}(Y;\mathrm {Sp})$ to local systems give ![]() $f_!\cong f_*: \mathrm {Loc}(X;\mathrm {Sp})\to \mathrm {Loc}(Y;\mathrm {Sp})$, which is the left adjoint of
$f_!\cong f_*: \mathrm {Loc}(X;\mathrm {Sp})\to \mathrm {Loc}(Y;\mathrm {Sp})$, which is the left adjoint of ![]() $f^!: \mathrm {Loc}(Y;\mathrm {Sp})\to \mathrm {Loc}(X;\mathrm {Sp})$. The unit and co-unit for the above pair of adjoints in
$f^!: \mathrm {Loc}(Y;\mathrm {Sp})\to \mathrm {Loc}(X;\mathrm {Sp})$. The unit and co-unit for the above pair of adjoints in ![]() $(\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}})^{\mathrm {Sp}//}$ induce the unit and co-unit for the restriction on the full subcategory of local systems. Moreover, all functors involved are continuous.
$(\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}})^{\mathrm {Sp}//}$ induce the unit and co-unit for the restriction on the full subcategory of local systems. Moreover, all functors involved are continuous.
Let ![]() $\mathbb {T}_{\mathrm {V}\mathrm {S}_{\mathrm {LCH}}}$ be the restriction
$\mathbb {T}_{\mathrm {V}\mathrm {S}_{\mathrm {LCH}}}$ be the restriction ![]() $\mathrm {Loc}^!_{!;\mathrm {Sp} //}$ to
$\mathrm {Loc}^!_{!;\mathrm {Sp} //}$ to ![]() $\mathrm {V}\mathrm {S}_{\mathrm {LCH}}^{\rm op}$, which factors through
$\mathrm {V}\mathrm {S}_{\mathrm {LCH}}^{\rm op}$, which factors through ![]() $(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}/}$.
$(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}/}$.
Corollary A.11 The functor ![]() $\mathbb {T}_{\mathrm {V}\mathrm {S}_{\mathrm {LCH}}}$ satisfies the right Beck–Chevalley condition with respect to
$\mathbb {T}_{\mathrm {V}\mathrm {S}_{\mathrm {LCH}}}$ satisfies the right Beck–Chevalley condition with respect to ![]() $\mathsf {propfib}'$. In particular, for any
$\mathsf {propfib}'$. In particular, for any ![]() $(f, \varphi ): (V, X)\to (V',Y)$ with
$(f, \varphi ): (V, X)\to (V',Y)$ with ![]() $f$ a proper locally trivial fibration,
$f$ a proper locally trivial fibration, ![]() $\mathbb {T}_{\mathrm {V}\mathrm {S}_{\mathrm {LCH}}}(f,\varphi )$ in
$\mathbb {T}_{\mathrm {V}\mathrm {S}_{\mathrm {LCH}}}(f,\varphi )$ in ![]() $(\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}/ /}$ is left adjointable.
$(\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}/ /}$ is left adjointable.
Proposition A.12 There is a natural symmetric monoidal functor

that factors through ![]() $(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}/}$, and it satisfies the right Beck–Chevalley condition with respect to
$(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}/}$, and it satisfies the right Beck–Chevalley condition with respect to ![]() $\mathsf {propfib}'$.
$\mathsf {propfib}'$.
Proof. Take the restriction of ![]() $\mathbb {T}_{\mathrm {V}\mathrm {S}_{\mathrm {LCH}}}$ to
$\mathbb {T}_{\mathrm {V}\mathrm {S}_{\mathrm {LCH}}}$ to ![]() $(\mathrm {VTop}^{\rm lc})^{\rm op}$, where
$(\mathrm {VTop}^{\rm lc})^{\rm op}$, where ![]() $\mathrm {VTop}^{\rm lc}=\mathrm {VTop}\cap \mathrm {V}\mathrm {S}_{\mathrm {LCH}}$, and then define
$\mathrm {VTop}^{\rm lc}=\mathrm {VTop}\cap \mathrm {V}\mathrm {S}_{\mathrm {LCH}}$, and then define ![]() $\mathbb {T}_{\mathrm {VTop}}$ to be the right Kan extension along the full (symmetric monoidal) embedding
$\mathbb {T}_{\mathrm {VTop}}$ to be the right Kan extension along the full (symmetric monoidal) embedding ![]() $(\mathrm {VTop}^{\rm lc})^{\rm op}\hookrightarrow (\mathrm {VTop})^{\rm op}$. It is not hard to check that:
$(\mathrm {VTop}^{\rm lc})^{\rm op}\hookrightarrow (\mathrm {VTop})^{\rm op}$. It is not hard to check that:
–
 $\mathbb {T}_{\mathrm {VTop}}(p:VG\to G)\simeq \varprojlim _{N}\mathbb {T}_{\mathrm {V}\mathrm {S}_{\mathrm {LCH}}}(VG_N\to G_N)\simeq \big (p_*\varpi _{VG}\in \mathrm {Loc}(G;\mathrm {Sp})\big )$;
$\mathbb {T}_{\mathrm {VTop}}(p:VG\to G)\simeq \varprojlim _{N}\mathbb {T}_{\mathrm {V}\mathrm {S}_{\mathrm {LCH}}}(VG_N\to G_N)\simeq \big (p_*\varpi _{VG}\in \mathrm {Loc}(G;\mathrm {Sp})\big )$;– for any
 $p_V: V\to X$ classified by
$p_V: V\to X$ classified by  $\nu _{V}: X\to G$,
$\nu _{V}: X\to G$,  $\mathbb {T}_{\mathrm {VTop}}(p_V)\simeq \big (\nu _V^!p_*\varpi _{VG}\in \mathrm {Loc}(X;\mathrm {Sp})\big )$.
$\mathbb {T}_{\mathrm {VTop}}(p_V)\simeq \big (\nu _V^!p_*\varpi _{VG}\in \mathrm {Loc}(X;\mathrm {Sp})\big )$.
For any CW-complex ![]() $X=\mathrm {colim }_n(X_0\subset X_1\subset X_2\cdots )$ and any vector bundle
$X=\mathrm {colim }_n(X_0\subset X_1\subset X_2\cdots )$ and any vector bundle ![]() $p_V: V\to X$, let
$p_V: V\to X$, let ![]() $p_{V_n}: V_n:=V|_{X_n}\to X_n$. Then
$p_{V_n}: V_n:=V|_{X_n}\to X_n$. Then ![]() $\mathbb {T}_{\mathrm {VTop}}(p_V)\overset {\sim }{\to }\varprojlim _n\mathbb {T}_{\mathrm {VTop}}(p_{V_n})$. For any
$\mathbb {T}_{\mathrm {VTop}}(p_V)\overset {\sim }{\to }\varprojlim _n\mathbb {T}_{\mathrm {VTop}}(p_{V_n})$. For any ![]() $(f, \varphi ): (V',Y)\to (V,X)$ in
$(f, \varphi ): (V',Y)\to (V,X)$ in ![]() $\mathsf {propfib}'$, let
$\mathsf {propfib}'$, let ![]() $Y_n=f^{-1}(X_n)$. Now using induction on
$Y_n=f^{-1}(X_n)$. Now using induction on ![]() $n$, the pushout diagrams for cell attachments (on
$n$, the pushout diagrams for cell attachments (on ![]() $X_n$ to get
$X_n$ to get ![]() $X_{n+1}$) and Corollary A.11, one can easily show that
$X_{n+1}$) and Corollary A.11, one can easily show that ![]() $\mathbb {T}_{\mathrm {VTop}}(f, \varphi )$ is left adjointable. It also follows easily that
$\mathbb {T}_{\mathrm {VTop}}(f, \varphi )$ is left adjointable. It also follows easily that ![]() $\mathbb {T}_{\mathrm {VTop}}$ satisfies the right Beck–Chevalley condition with respect to
$\mathbb {T}_{\mathrm {VTop}}$ satisfies the right Beck–Chevalley condition with respect to ![]() $\mathsf {propfib}'$.
$\mathsf {propfib}'$.
Lastly, the symmetric monoidal structure of ![]() $\mathbb {T}_{\mathrm {VTop}}$ follows from [Reference Gaitsgory and RozenblyumGR17, Chapter 9, 3.2.2].
$\mathbb {T}_{\mathrm {VTop}}$ follows from [Reference Gaitsgory and RozenblyumGR17, Chapter 9, 3.2.2].
A.2.2  $\mathcal {V}\mathcal {S}\mathrm {pc}$ as a localization of
$\mathcal {V}\mathcal {S}\mathrm {pc}$ as a localization of  $\mathrm {VTop}$
$\mathrm {VTop}$
Let ![]() $W$ be the collection of weak equivalences in
$W$ be the collection of weak equivalences in ![]() $\mathrm {Top}$. Let
$\mathrm {Top}$. Let ![]() $W'$ be the corresponding class of morphisms in
$W'$ be the corresponding class of morphisms in ![]() $\mathrm {VTop}$, which we refer as weak equivalences. Clearly
$\mathrm {VTop}$, which we refer as weak equivalences. Clearly ![]() $W'$ is closed under the symmetric monoidal structure. Then we have the following.Footnote 10
$W'$ is closed under the symmetric monoidal structure. Then we have the following.Footnote 10
Proposition A.13 The simplicial localization category ![]() $\mathrm {VTop}[(W')^{-1}]$ (by Dwyer–Kan), viewed as a symmetric monoidal
$\mathrm {VTop}[(W')^{-1}]$ (by Dwyer–Kan), viewed as a symmetric monoidal ![]() $\infty$-category through the coherent nerve functor
$\infty$-category through the coherent nerve functor ![]() $N$, is naturally equivalent to
$N$, is naturally equivalent to ![]() $\mathcal {V}\mathcal {S}\mathrm {pc}$.
$\mathcal {V}\mathcal {S}\mathrm {pc}$.
Proof. There is an obvious functor

where the upper morphism in the bottom Cartesian diagram is the tautological one.
Let ![]() $\mathrm {Fib}$ (respectively,
$\mathrm {Fib}$ (respectively, ![]() $\mathrm {Cof}$) be the class of fibrations (respectively, cofibrations) in
$\mathrm {Cof}$) be the class of fibrations (respectively, cofibrations) in ![]() $\mathrm {Top}$. Let
$\mathrm {Top}$. Let ![]() $\mathrm {Fib}'$ (respectively,
$\mathrm {Fib}'$ (respectively, ![]() $\mathrm {Cof}'$) be the corresponding class of morphisms in
$\mathrm {Cof}'$) be the corresponding class of morphisms in ![]() $\mathrm {VTop}$. Let
$\mathrm {VTop}$. Let
We calculate the hammock localization ![]() $L^{\rm H}(\mathrm {VTop}):=L^{\rm H}(\mathrm {VTop}, W')$ as in [Reference Dwyer and KanDK80]. We will mainly follow the proof of Proposition 4.4 from [Reference Dwyer and KanDK80, §7.2]. Since
$L^{\rm H}(\mathrm {VTop}):=L^{\rm H}(\mathrm {VTop}, W')$ as in [Reference Dwyer and KanDK80]. We will mainly follow the proof of Proposition 4.4 from [Reference Dwyer and KanDK80, §7.2]. Since ![]() $\mathrm {VTop}$ is not a model category (for it doesn't admit a terminal object), the statement of that proposition doesn't directly apply. In the following, we use
$\mathrm {VTop}$ is not a model category (for it doesn't admit a terminal object), the statement of that proposition doesn't directly apply. In the following, we use ![]() $\overset {\sim }{\rightarrowtail }$,
$\overset {\sim }{\rightarrowtail }$, ![]() $\overset {\sim }{\twoheadrightarrow }$ to represent the classes
$\overset {\sim }{\twoheadrightarrow }$ to represent the classes ![]() $W'_\mathrm {Cof}, W'_\mathrm {Fib}$ (respectively,
$W'_\mathrm {Cof}, W'_\mathrm {Fib}$ (respectively, ![]() $W_\mathrm {Cof}, W_\mathrm {Fib}$) in
$W_\mathrm {Cof}, W_\mathrm {Fib}$) in ![]() $\mathrm {VTop}$ (respectively,
$\mathrm {VTop}$ (respectively, ![]() $\mathrm {Top}$), respectively.
$\mathrm {Top}$), respectively.
Step 1: set-up of ![]() $L^{\rm H}(\mathrm {VTop}, W'_\mathrm {Fib})$. Since
$L^{\rm H}(\mathrm {VTop}, W'_\mathrm {Fib})$. Since ![]() $\mathrm {VTop}$ admits pushout and pullback in the obvious way, using [Reference Dwyer and KanDK80, Proposition 8.1] and its dual version, we know that
$\mathrm {VTop}$ admits pushout and pullback in the obvious way, using [Reference Dwyer and KanDK80, Proposition 8.1] and its dual version, we know that ![]() $(\mathrm {VTop}, W'_{\mathrm {Fib}})$ (respectively,
$(\mathrm {VTop}, W'_{\mathrm {Fib}})$ (respectively, ![]() $(\mathrm {VTop}, W'_{\mathrm {Cof}})$) admits a homotopy calculus of right (respectively, left) fractions. Moreover, if we set
$(\mathrm {VTop}, W'_{\mathrm {Cof}})$) admits a homotopy calculus of right (respectively, left) fractions. Moreover, if we set ![]() $W_1=W_{\mathrm {Cof}}', W_2=W_{\mathrm {Fib}}'$ in [Reference Dwyer and KanDK80, Proposition 8.2], then we get the pair
$W_1=W_{\mathrm {Cof}}', W_2=W_{\mathrm {Fib}}'$ in [Reference Dwyer and KanDK80, Proposition 8.2], then we get the pair ![]() $(\mathrm {VTop}, W')$ admits a homotopy calculus of (two-sided) fractions. Using [Reference Dwyer and KanDK80, Proposition 6.2], the reduction map
$(\mathrm {VTop}, W')$ admits a homotopy calculus of (two-sided) fractions. Using [Reference Dwyer and KanDK80, Proposition 6.2], the reduction map
is a weak equivalence. For any ![]() $(V, X), (E, Y)\in \mathrm {VTop}$, recall that
$(V, X), (E, Y)\in \mathrm {VTop}$, recall that ![]() $\mathrm {Hom}_{(\mathrm {VTop})(W'_\mathrm {Fib})^{-1}}\big ((V, X), (E, Y)\big )$ is, by definition, the nerve of all diagrams
$\mathrm {Hom}_{(\mathrm {VTop})(W'_\mathrm {Fib})^{-1}}\big ((V, X), (E, Y)\big )$ is, by definition, the nerve of all diagrams
Following [Reference Dwyer and KanDK80, § 7.2(iii)], let ![]() $S=(W\downarrow X)$ be the category of the trivial fibrations in
$S=(W\downarrow X)$ be the category of the trivial fibrations in ![]() $\mathrm {Top}$ ending at
$\mathrm {Top}$ ending at ![]() $X$, and let
$X$, and let ![]() $S'=(W'\downarrow (V, X))$ be the category of
$S'=(W'\downarrow (V, X))$ be the category of ![]() $(V',X')\overset {\sim }{\twoheadrightarrow } (V, X)$ ending at
$(V',X')\overset {\sim }{\twoheadrightarrow } (V, X)$ ending at ![]() $(V,X)$. Let
$(V,X)$. Let
 \begin{align*} K': (S')^{\rm op}&\to \mathrm{Sets}\subset \mathcal{S}\mathrm{et}_{\Delta}\\ ((V',X')\overset{\sim}{\twoheadrightarrow} (V, X))&\mapsto \mathrm{Hom}_{\mathrm{VTop}}((V',X'), (E, Y)). \end{align*}
\begin{align*} K': (S')^{\rm op}&\to \mathrm{Sets}\subset \mathcal{S}\mathrm{et}_{\Delta}\\ ((V',X')\overset{\sim}{\twoheadrightarrow} (V, X))&\mapsto \mathrm{Hom}_{\mathrm{VTop}}((V',X'), (E, Y)). \end{align*}
Then ![]() $\mathrm {Hom}_{(\mathrm {VTop})(W'_\mathrm {Fib})^{-1}}\big ((V, X), (E, Y)\big )$ is weakly equivalent to the (homotopy) colimit of
$\mathrm {Hom}_{(\mathrm {VTop})(W'_\mathrm {Fib})^{-1}}\big ((V, X), (E, Y)\big )$ is weakly equivalent to the (homotopy) colimit of ![]() $K'$. By [Reference Dwyer and KanDK80, Proposition 6.12], for any special cosimplicial resolution
$K'$. By [Reference Dwyer and KanDK80, Proposition 6.12], for any special cosimplicial resolution ![]() $X^\bullet$ of
$X^\bullet$ of ![]() $X\in \mathrm {Top}$, the functor
$X\in \mathrm {Top}$, the functor ![]() $x: \Delta \to (W\downarrow X)$ which sends
$x: \Delta \to (W\downarrow X)$ which sends ![]() $[n]$ to
$[n]$ to ![]() $X^n\overset {\sim }{\twoheadrightarrow } X$ is left cofinal. Since the projection
$X^n\overset {\sim }{\twoheadrightarrow } X$ is left cofinal. Since the projection ![]() $(S')^{\rm op}\to S^{\rm op}$ is an equivalence, for any such a special cosimplicial resolution
$(S')^{\rm op}\to S^{\rm op}$ is an equivalence, for any such a special cosimplicial resolution ![]() $X^\bullet$, we have
$X^\bullet$, we have
where ![]() $V^n\to X^n$ is the pullback of
$V^n\to X^n$ is the pullback of ![]() $V\to X$ along
$V\to X$ along ![]() $X^n\overset {\sim }{\twoheadrightarrow } X$. It is clear from the definition of a special cosimplicial resolution (cf. [Reference Dwyer and KanDK80, § 4.3 and Remark 6.8]) that to give such a
$X^n\overset {\sim }{\twoheadrightarrow } X$. It is clear from the definition of a special cosimplicial resolution (cf. [Reference Dwyer and KanDK80, § 4.3 and Remark 6.8]) that to give such a ![]() $X^\bullet$, one just needs to find a special cosimplicial resolution
$X^\bullet$, one just needs to find a special cosimplicial resolution ![]() $C^\bullet$ of
$C^\bullet$ of ![]() $\mathit {pt}$ and then take the product with
$\mathit {pt}$ and then take the product with ![]() $X$.
$X$.
Step 2: calculation of (A.2.9). Let ![]() $X^\bullet =X\times C^\bullet$ and
$X^\bullet =X\times C^\bullet$ and ![]() $V^\bullet =V\times C^\bullet$. First assume that the vector bundle
$V^\bullet =V\times C^\bullet$. First assume that the vector bundle ![]() $E\to Y$ (respectively,
$E\to Y$ (respectively, ![]() $V\to X$) has constant rank
$V\to X$) has constant rank ![]() $r$, so then it is classified by a (continuous) map
$r$, so then it is classified by a (continuous) map ![]() $\nu _E: Y\to BO(r)$ (respectively,
$\nu _E: Y\to BO(r)$ (respectively, ![]() $\nu _V: X\to BO(r)$). Let
$\nu _V: X\to BO(r)$). Let ![]() $E_{\nu _V}O(r)\to X\times BO(r)$ be the universal
$E_{\nu _V}O(r)\to X\times BO(r)$ be the universal ![]() $O(r)$-torsor relative to the section
$O(r)$-torsor relative to the section ![]() $(id_X,\nu _V): X\to X\times BO(r)$, i.e.
$(id_X,\nu _V): X\to X\times BO(r)$, i.e. ![]() $E_{\nu _V}O(r)$ is isomorphic to
$E_{\nu _V}O(r)$ is isomorphic to ![]() $(X\times BO(r))_{(id_X,\nu _V)/}$ in
$(X\times BO(r))_{(id_X,\nu _V)/}$ in ![]() $\mathcal {S}\mathrm {pc}_{/X}$.
$\mathcal {S}\mathrm {pc}_{/X}$.
By adjunction, the (diagonal of the bi)simplicial set ![]() $\mathrm {Hom}_{\mathrm {VTop}}((V^\bullet, X^\bullet ), (E, Y))$ is weakly equivalent to
$\mathrm {Hom}_{\mathrm {VTop}}((V^\bullet, X^\bullet ), (E, Y))$ is weakly equivalent to
 \begin{align} &\mathrm{Maps}_{\mathcal{S}\mathrm{pc}}(X, Y)\underset{\mathrm{Maps}_{\mathcal{S}\mathrm{pc}}(X,BO(r))}{\times} \mathrm{Maps}_{\mathcal{S}\mathrm{pc}_{/X}}(X, E_{\nu_V}O(r))\nonumber\\ &\quad \simeq \mathrm{Maps}_{\mathcal{S}\mathrm{pc}_{/BO(r)}}(\nu_V, \nu_E) \end{align}
\begin{align} &\mathrm{Maps}_{\mathcal{S}\mathrm{pc}}(X, Y)\underset{\mathrm{Maps}_{\mathcal{S}\mathrm{pc}}(X,BO(r))}{\times} \mathrm{Maps}_{\mathcal{S}\mathrm{pc}_{/X}}(X, E_{\nu_V}O(r))\nonumber\\ &\quad \simeq \mathrm{Maps}_{\mathcal{S}\mathrm{pc}_{/BO(r)}}(\nu_V, \nu_E) \end{align}
where the map ![]() $\mathrm {Maps}_{\mathcal {S}\mathrm {pc}}(X, Y)\to \mathrm {Maps}_{\mathcal {S}\mathrm {pc}}(X,BO(r))$ is induced from
$\mathrm {Maps}_{\mathcal {S}\mathrm {pc}}(X, Y)\to \mathrm {Maps}_{\mathcal {S}\mathrm {pc}}(X,BO(r))$ is induced from ![]() $\nu _E$.
$\nu _E$.
If ![]() $E\to Y$ is not necessarily of constant rank, then (A.2.10) directly extends to
$E\to Y$ is not necessarily of constant rank, then (A.2.10) directly extends to
Step 3: ![]() $L^{\rm H}((\mathrm {Top}_{/G})^f, W_\mathrm {Fib})\to L^{\rm H}(\mathrm {VTop}, W'_\mathrm {Fib})$ is a weak equivalence. Here
$L^{\rm H}((\mathrm {Top}_{/G})^f, W_\mathrm {Fib})\to L^{\rm H}(\mathrm {VTop}, W'_\mathrm {Fib})$ is a weak equivalence. Here ![]() $(\mathrm {Top}_{/G})^f$ is the full subcategory of
$(\mathrm {Top}_{/G})^f$ is the full subcategory of ![]() $\mathrm {Top}_{/G}$ consisting of fibrant objects. Using the same cosimplicial resolution
$\mathrm {Top}_{/G}$ consisting of fibrant objects. Using the same cosimplicial resolution ![]() $X^\bullet$ as above (now with
$X^\bullet$ as above (now with ![]() $\nu _V: X\to G$ and
$\nu _V: X\to G$ and ![]() $\nu _E: Y\to G$ being fibrations), we have the following commutative diagram up to homotopy.
$\nu _E: Y\to G$ being fibrations), we have the following commutative diagram up to homotopy.

Hence, the functor ![]() $N(L^{\rm H}((\mathrm {Top}_{/G})^f, W_\mathrm {Fib}))\to N(L^{\rm H}(\mathrm {VTop}, W'_\mathrm {Fib}))$ is fully faithful. Using Step 2, we also know that the functor is essentially surjective.
$N(L^{\rm H}((\mathrm {Top}_{/G})^f, W_\mathrm {Fib}))\to N(L^{\rm H}(\mathrm {VTop}, W'_\mathrm {Fib}))$ is fully faithful. Using Step 2, we also know that the functor is essentially surjective.
Step 4: ![]() $\mathcal {V}\mathcal {S}\mathrm {pc}\simeq N(L^{\rm H}(\mathrm {Top}_{/G}, W))\to N(L^{\rm H}(\mathrm {VTop}, W'))$ is an equivalence. From the calculation in Step 3, we see that
$\mathcal {V}\mathcal {S}\mathrm {pc}\simeq N(L^{\rm H}(\mathrm {Top}_{/G}, W))\to N(L^{\rm H}(\mathrm {VTop}, W'))$ is an equivalence. From the calculation in Step 3, we see that ![]() $N(L^{\rm H}((\mathrm {Top}_{/G})^f, W_{\mathrm {Fib}})\to N(L^{\rm H}(\mathrm {Top}_{/G}, W)))\simeq \mathcal {S}\mathrm {pc}_{/G}\simeq \mathcal {V}\mathcal {S}\mathrm {pc}$ is an equivalence. From the same step, we have a weak equivalence
$N(L^{\rm H}((\mathrm {Top}_{/G})^f, W_{\mathrm {Fib}})\to N(L^{\rm H}(\mathrm {Top}_{/G}, W)))\simeq \mathcal {S}\mathrm {pc}_{/G}\simeq \mathcal {V}\mathcal {S}\mathrm {pc}$ is an equivalence. From the same step, we have a weak equivalence ![]() $L^{\rm H}(\mathrm {VTop}, W'_\mathrm {Fib})\to L^{\rm H}(\mathrm {Top}_{/G}, W)$. Then by the universal property of Dwyer–Kan localization, we know that
$L^{\rm H}(\mathrm {VTop}, W'_\mathrm {Fib})\to L^{\rm H}(\mathrm {Top}_{/G}, W)$. Then by the universal property of Dwyer–Kan localization, we know that
and the desired equivalence follows.
Lastly, ![]() $N(L^{\rm H}(\mathrm {VTop}, W'))\to N(L^{\rm H}(\mathrm {Top}, W))\simeq \mathcal {S}\mathrm {pc}$ is naturally a symmetric monoidal functor and it is a commutative algebra object in
$N(L^{\rm H}(\mathrm {VTop}, W'))\to N(L^{\rm H}(\mathrm {Top}, W))\simeq \mathcal {S}\mathrm {pc}$ is naturally a symmetric monoidal functor and it is a commutative algebra object in ![]() $\mathrm {LFib}_{\mathcal {S}\mathrm {pc}}$ as in [Reference RamziRam22, Corollary C] (see also [Reference LurieLur17] and [Reference HinichHin15, Appendix A.2]). Now by the monoidal version of straightening in [Reference RamziRam22] and [Reference Gaitsgory and RozenblyumGR17, Chapter 9, 3.2.2], to see that the symmetric monoidal structure on
$\mathrm {LFib}_{\mathcal {S}\mathrm {pc}}$ as in [Reference RamziRam22, Corollary C] (see also [Reference LurieLur17] and [Reference HinichHin15, Appendix A.2]). Now by the monoidal version of straightening in [Reference RamziRam22] and [Reference Gaitsgory and RozenblyumGR17, Chapter 9, 3.2.2], to see that the symmetric monoidal structure on ![]() $N(L^{\rm H}(\mathrm {VTop}, W'))$ is equivalent to that on
$N(L^{\rm H}(\mathrm {VTop}, W'))$ is equivalent to that on ![]() $\mathcal {V}\mathcal {S}\mathrm {pc}$ as objects in
$\mathcal {V}\mathcal {S}\mathrm {pc}$ as objects in ![]() $\mathrm {LFib}_{\mathcal {S}\mathrm {pc}}$ (which are both classified by functors
$\mathrm {LFib}_{\mathcal {S}\mathrm {pc}}$ (which are both classified by functors ![]() $\mathcal {S}\mathrm {pc}^{\rm op}\to \mathcal {S}\mathrm {pc}$ that are the right Kan extension of their restriction to
$\mathcal {S}\mathrm {pc}^{\rm op}\to \mathcal {S}\mathrm {pc}$ that are the right Kan extension of their restriction to ![]() $\{pt\}$), it suffices to check that
$\{pt\}$), it suffices to check that
has the same symmetric monoidal structure on ![]() $N(\mathrm {Vect}_\mathbf {R}^{\simeq })$. However, the calculation from Steps 1 and 2 for (objects in)
$N(\mathrm {Vect}_\mathbf {R}^{\simeq })$. However, the calculation from Steps 1 and 2 for (objects in) ![]() $\mathrm {VTop}\underset {\mathrm {Top}}{\times }\{pt\}$ (which only involves objects from
$\mathrm {VTop}\underset {\mathrm {Top}}{\times }\{pt\}$ (which only involves objects from ![]() $\mathrm {VTop}\times _{\mathrm {Top}}\{|\Delta ^n|\}, n\geq 0$) exactly gives a standard definition of
$\mathrm {VTop}\times _{\mathrm {Top}}\{|\Delta ^n|\}, n\geq 0$) exactly gives a standard definition of ![]() $N(\mathrm {Vect}_\mathbf {R}^{\simeq })$ and its symmetric monoidal structure.
$N(\mathrm {Vect}_\mathbf {R}^{\simeq })$ and its symmetric monoidal structure.
Corollary A.14 The symmetric monoidal functor ![]() $\mathbb {T}_{\mathrm {VTop}}$ (A.2.8) descends to a symmetric monoidal functor
$\mathbb {T}_{\mathrm {VTop}}$ (A.2.8) descends to a symmetric monoidal functor

that factors through ![]() $(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}/}$, and it satisfies the right Beck–Chevalley condition with respect to
$(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}/}$, and it satisfies the right Beck–Chevalley condition with respect to ![]() $\mathsf {hpf}'$.
$\mathsf {hpf}'$.
A.2.3 The isomorphism  $\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}\cong \mathbb {T}$
$\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}\cong \mathbb {T}$
Corollary A.15 The symmetric monoidal functor ![]() $\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}$ is isomorphic to
$\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}$ is isomorphic to ![]() $\mathbb {T}$ (A.1.1).
$\mathbb {T}$ (A.1.1).
Proof. Since both functors are the right Kan extension from their respective restrictions to ![]() $(\mathcal {V}\mathcal {S}\mathrm {pc}\times _{\mathcal {S}\mathrm {pc}}\{\mathit {pt}\})^{\rm op}\simeq N(\mathrm {Vect}_\mathbf {R}^{\simeq })^{\rm op}$, using [Reference Gaitsgory and RozenblyumGR17, Chapter 9, 3.2.2] again, it suffices to show that they agree on this full (symmetric monoidal) subcategory. By looking at
$(\mathcal {V}\mathcal {S}\mathrm {pc}\times _{\mathcal {S}\mathrm {pc}}\{\mathit {pt}\})^{\rm op}\simeq N(\mathrm {Vect}_\mathbf {R}^{\simeq })^{\rm op}$, using [Reference Gaitsgory and RozenblyumGR17, Chapter 9, 3.2.2] again, it suffices to show that they agree on this full (symmetric monoidal) subcategory. By looking at ![]() $\mathbb {T}_{\mathrm {VTop}}|_{(\mathrm {VTop}\times _{\mathrm {Top}}\{\mathit {pt}\})^{\rm op}}$ and the calculation of the ‘function complex’ in the hammock localization (Steps 1 and 2 in the proof of Proposition A.13), we see that
$\mathbb {T}_{\mathrm {VTop}}|_{(\mathrm {VTop}\times _{\mathrm {Top}}\{\mathit {pt}\})^{\rm op}}$ and the calculation of the ‘function complex’ in the hammock localization (Steps 1 and 2 in the proof of Proposition A.13), we see that ![]() $\mathbb {T}|_{(\mathcal {V}\mathcal {S}\mathrm {pc}\times _{\mathcal {S}\mathrm {pc}}\{\mathit {pt}\})^{\rm op}}$ agrees with the definition of
$\mathbb {T}|_{(\mathcal {V}\mathcal {S}\mathrm {pc}\times _{\mathcal {S}\mathrm {pc}}\{\mathit {pt}\})^{\rm op}}$ agrees with the definition of ![]() $J$ (see [Reference LurieLur15]) as a symmetric monoidal functor.
$J$ (see [Reference LurieLur15]) as a symmetric monoidal functor.
A.3 A symmetric monoidal extension of  $\mathbb {T}_{\mathrm {VTop}}$ and
$\mathbb {T}_{\mathrm {VTop}}$ and  $\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}$ to correspondences
$\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}$ to correspondences
The class ![]() $\mathsf {propfib}$ in
$\mathsf {propfib}$ in ![]() $\mathrm {Top}$ determines an isomorphism class of morphisms in
$\mathrm {Top}$ determines an isomorphism class of morphisms in ![]() $\mathcal {S}\mathrm {pc}$ through the localization
$\mathcal {S}\mathrm {pc}$ through the localization ![]() $\mathrm {Top}\to N(\mathrm {Top}[W^{-1}])\simeq \mathcal {S}\mathrm {pc}$. We denote the resulting class by
$\mathrm {Top}\to N(\mathrm {Top}[W^{-1}])\simeq \mathcal {S}\mathrm {pc}$. We denote the resulting class by ![]() $\mathsf {hpf}$. Concretely, every morphism in
$\mathsf {hpf}$. Concretely, every morphism in ![]() $\mathsf {hpf}$ is a finite composition of proper locally trivial fibrations and zig-zags of weak equivalences. Clearly,
$\mathsf {hpf}$ is a finite composition of proper locally trivial fibrations and zig-zags of weak equivalences. Clearly, ![]() $\mathsf {hpf}$ is closed under compositions, homotopy pullbacks (along any morphism) and taking Cartesian products. Let
$\mathsf {hpf}$ is closed under compositions, homotopy pullbacks (along any morphism) and taking Cartesian products. Let ![]() $\mathsf {hpf}'$ be the preimage of
$\mathsf {hpf}'$ be the preimage of ![]() $\mathsf {hpf}$ under
$\mathsf {hpf}$ under ![]() $\mathcal {V}\mathcal {S}\mathrm {pc}\to \mathcal {S}\mathrm {pc}$.
$\mathcal {V}\mathcal {S}\mathrm {pc}\to \mathcal {S}\mathrm {pc}$.
In order to prove Proposition 4.13, we need to extend the functors ![]() $\mathbb {T}_{\mathrm {VTop}}$ and
$\mathbb {T}_{\mathrm {VTop}}$ and ![]() $\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}$ to
$\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}$ to ![]() $\mathrm {Corr}(\mathrm {VTop})_{\mathsf {propfib}',\mathsf {all}}$ and
$\mathrm {Corr}(\mathrm {VTop})_{\mathsf {propfib}',\mathsf {all}}$ and ![]() $\mathrm {Corr}(\mathcal {V}\mathcal {S}\mathrm {pc})_{\mathsf {hpf}',\mathsf {all}}$, respectively. Ideally, we would like to apply the various extension results from [Reference Gaitsgory and RozenblyumGR17, Chapter 8,9]. However, the results stated in [Reference Gaitsgory and RozenblyumGR17, Chapter 8,9] that we need require the class of vertical arrows to satisfy the ‘2-out-of-3’ condition (cf. [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 1.1.1 (5)]). Since the classes
$\mathrm {Corr}(\mathcal {V}\mathcal {S}\mathrm {pc})_{\mathsf {hpf}',\mathsf {all}}$, respectively. Ideally, we would like to apply the various extension results from [Reference Gaitsgory and RozenblyumGR17, Chapter 8,9]. However, the results stated in [Reference Gaitsgory and RozenblyumGR17, Chapter 8,9] that we need require the class of vertical arrows to satisfy the ‘2-out-of-3’ condition (cf. [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 1.1.1 (5)]). Since the classes ![]() $\mathsf {propfib}'$ and
$\mathsf {propfib}'$ and ![]() $\mathsf {hpf}'$ certainly do not satisfy ‘2-out-of-3’ (and we are not aware of a better candidate that satisfies ‘2-out-of-3’), we need to essentially go back to the proof of some of those extension results and make them work in our setting. We remark that ‘2-out-of-3’ is needed in [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 1.1.1 (5)] mostly for establishing uniqueness of extensions of functors. Here we are aiming at proving Proposition A.22, which does not involve uniqueness of the extensions.
$\mathsf {hpf}'$ certainly do not satisfy ‘2-out-of-3’ (and we are not aware of a better candidate that satisfies ‘2-out-of-3’), we need to essentially go back to the proof of some of those extension results and make them work in our setting. We remark that ‘2-out-of-3’ is needed in [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 1.1.1 (5)] mostly for establishing uniqueness of extensions of functors. Here we are aiming at proving Proposition A.22, which does not involve uniqueness of the extensions.
A.3.1 The formalism of universal adjoint functors and symmetric monoidal upgrades
Recall the formalism of the universal adjointable functor from [Reference Gaitsgory and RozenblyumGR17, Chapter 12, § 1.2, 1.3]. For any ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\mathbf {C}$ and a 1-full subcategory
$\mathbf {C}$ and a 1-full subcategory ![]() $\mathcal {D}\subset \mathbf {C}^{1\text {-}\mathcal {C}\mathrm {at}}$ such that
$\mathcal {D}\subset \mathbf {C}^{1\text {-}\mathcal {C}\mathrm {at}}$ such that ![]() $\mathcal {D}^{\mathcal {S}\mathrm {pc}}=\mathbf {C}^{\mathcal {S}\mathrm {pc}}$, there is a universal recipient of functors left-adjointable with respect to
$\mathcal {D}^{\mathcal {S}\mathrm {pc}}=\mathbf {C}^{\mathcal {S}\mathrm {pc}}$, there is a universal recipient of functors left-adjointable with respect to ![]() $\mathcal {D}$, denoted by
$\mathcal {D}$, denoted by ![]() $\mathbf {C}^{R_{\mathcal {D}}}$. This
$\mathbf {C}^{R_{\mathcal {D}}}$. This ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\mathbf {C}^{R_{\mathcal {D}}}$ has an explicit description as
$\mathbf {C}^{R_{\mathcal {D}}}$ has an explicit description as
where ![]() $\mathrm {Sq}_{\bullet, \bullet }^{\mathrm {Pair}}: 2\text {-}\mathcal {C}\mathrm {at}^{\mathrm {Pair}}\to \mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}}$ is defined in [Reference Gaitsgory and RozenblyumGR17, Chapter 10, 4.3.3] and
$\mathrm {Sq}_{\bullet, \bullet }^{\mathrm {Pair}}: 2\text {-}\mathcal {C}\mathrm {at}^{\mathrm {Pair}}\to \mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}}$ is defined in [Reference Gaitsgory and RozenblyumGR17, Chapter 10, 4.3.3] and ![]() $\mathfrak {L}^{\mathrm {Sq}}$ is the left adjoint of
$\mathfrak {L}^{\mathrm {Sq}}$ is the left adjoint of ![]() $\mathrm {Sq}_{\bullet, \bullet }: 2\text {-}\mathcal {C}\mathrm {at}\to \mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}}$. In the special case that
$\mathrm {Sq}_{\bullet, \bullet }: 2\text {-}\mathcal {C}\mathrm {at}\to \mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}}$. In the special case that ![]() $\mathcal {D}=\mathbf {C}^{1\text {-}\mathcal {C}\mathrm {at}}$,
$\mathcal {D}=\mathbf {C}^{1\text {-}\mathcal {C}\mathrm {at}}$, ![]() $\mathrm {Sq}_{\bullet,\bullet }^{\mathrm {Pair}}(\mathbf {C}^{2\text {-}{\rm op}}, \mathbf {C}^{1\text {-}\mathcal {C}\mathrm {at}})=\mathrm {Sq}_{\bullet,\bullet }(\mathbf {C}^{2\text {-}{\rm op}})$ from definition. The construction (A.3.1) is clearly functorial in
$\mathrm {Sq}_{\bullet,\bullet }^{\mathrm {Pair}}(\mathbf {C}^{2\text {-}{\rm op}}, \mathbf {C}^{1\text {-}\mathcal {C}\mathrm {at}})=\mathrm {Sq}_{\bullet,\bullet }(\mathbf {C}^{2\text {-}{\rm op}})$ from definition. The construction (A.3.1) is clearly functorial in ![]() $(\mathbf {C}, \mathcal {D})$ in the following sense.
$(\mathbf {C}, \mathcal {D})$ in the following sense.
(1) The assignment
 $(\mathbf {C}, \mathcal {D})\mapsto \mathbf {C}^{R_\mathcal {D}}$ gives a functor
$(\mathbf {C}, \mathcal {D})\mapsto \mathbf {C}^{R_\mathcal {D}}$ gives a functor  $R_{\mathrm {Pair}}: 2\text {-}\mathcal {C}\mathrm {at}^{\mathrm {Pair}}\to 2\text {-}\mathcal {C}\mathrm {at}$ (just following the formula (A.3.1)).
$R_{\mathrm {Pair}}: 2\text {-}\mathcal {C}\mathrm {at}^{\mathrm {Pair}}\to 2\text {-}\mathcal {C}\mathrm {at}$ (just following the formula (A.3.1)).(2) There is a natural transformation
 $\mathrm {OblvSubcat}\to R_{\mathrm {Pair}}$, where
$\mathrm {OblvSubcat}\to R_{\mathrm {Pair}}$, where  $\mathrm {OblvSubcat}: 2\text {-}\mathcal {C}\mathrm {at}^{\mathrm {Pair}}\to 2\text {-}\mathcal {C}\mathrm {at}$ is the forgetful functor that sends
$\mathrm {OblvSubcat}: 2\text {-}\mathcal {C}\mathrm {at}^{\mathrm {Pair}}\to 2\text {-}\mathcal {C}\mathrm {at}$ is the forgetful functor that sends  $(\mathbf {C}, \mathcal {D})\mapsto \mathbf {C}$. It is given by applying
$(\mathbf {C}, \mathcal {D})\mapsto \mathbf {C}$. It is given by applying  $\mathfrak {L}^{\mathrm {Sq}}$ to the tautological bi-simplicial functor
(A.3.2)
$\mathfrak {L}^{\mathrm {Sq}}$ to the tautological bi-simplicial functor
(A.3.2) \begin{equation} \mathrm{Sq}^{\tilde{}}_{\bullet, \bullet}(\mathbf{C})\simeq \mathrm{Sq}^{\tilde{}}_{\bullet, \bullet}(\mathbf{C}^{2\text{-}{\rm op}})^{\mathrm{vert}\text{-}\mathrm{op}}\hookrightarrow \mathrm{Sq}^{\mathrm{Pair}}_{\bullet, \bullet}(\mathbf{C}^{2\text{-}{\rm op}}, \mathcal{D})^{\mathrm{vert}\text{-}\mathrm{op}}, \end{equation}
\begin{equation} \mathrm{Sq}^{\tilde{}}_{\bullet, \bullet}(\mathbf{C})\simeq \mathrm{Sq}^{\tilde{}}_{\bullet, \bullet}(\mathbf{C}^{2\text{-}{\rm op}})^{\mathrm{vert}\text{-}\mathrm{op}}\hookrightarrow \mathrm{Sq}^{\mathrm{Pair}}_{\bullet, \bullet}(\mathbf{C}^{2\text{-}{\rm op}}, \mathcal{D})^{\mathrm{vert}\text{-}\mathrm{op}}, \end{equation}
Let ![]() $\mathrm {Maps}_{2\text {-}\mathcal {C}\mathrm {at}}(\mathbf {C}, \mathbf {X})^{R_\mathcal {D}}\subset \mathrm {Maps}_{2\text {-}\mathcal {C}\mathrm {at}}(\mathbf {C}, \mathbf {X})$ be the full subspace consisting of left-adjointable functors with respect to
$\mathrm {Maps}_{2\text {-}\mathcal {C}\mathrm {at}}(\mathbf {C}, \mathbf {X})^{R_\mathcal {D}}\subset \mathrm {Maps}_{2\text {-}\mathcal {C}\mathrm {at}}(\mathbf {C}, \mathbf {X})$ be the full subspace consisting of left-adjointable functors with respect to ![]() $\mathcal {D}$ (cf. [Reference Gaitsgory and RozenblyumGR17, Chapter 12, Definition 1.1.7]). Then the key statement of the formalism of the universal adjointable functor is the following.
$\mathcal {D}$ (cf. [Reference Gaitsgory and RozenblyumGR17, Chapter 12, Definition 1.1.7]). Then the key statement of the formalism of the universal adjointable functor is the following.
Theorem A.16 [Reference Gaitsgory and RozenblyumGR17, Chapter 12, Theorem 1.2.4]
Restricting along the canonical functor ![]() $\mathbf {C}\to \mathbf {C}^{R_\mathcal {D}}$ defines an isomorphism
$\mathbf {C}\to \mathbf {C}^{R_\mathcal {D}}$ defines an isomorphism
Let ![]() $\mathcal {W}$ be an
$\mathcal {W}$ be an ![]() $(\infty,1)$-category, and let
$(\infty,1)$-category, and let ![]() $\mathcal {W}'\subset \mathcal {W}$ be a full subcategory. For any morphism
$\mathcal {W}'\subset \mathcal {W}$ be a full subcategory. For any morphism ![]() $w_1\to w_2$ in
$w_1\to w_2$ in ![]() $\mathcal {W}$, we say it is a categorical epimorphism with respect to
$\mathcal {W}$, we say it is a categorical epimorphism with respect to ![]() $\mathcal {W}'$, if for every
$\mathcal {W}'$, if for every ![]() $w'\in \mathcal {W}'$, the morphism
$w'\in \mathcal {W}'$, the morphism
is a monomorphism of spaces, i.e. it is an embedding of certain connected components up to weak equivalences.
Corollary A.17 Assume ![]() $(\mathbf {C}^\otimes,\mathcal {D})\in \mathrm {CAlg}((2\text {-}\mathcal {C}\mathrm {at}^\mathrm {Pair})^\times )$. Let
$(\mathbf {C}^\otimes,\mathcal {D})\in \mathrm {CAlg}((2\text {-}\mathcal {C}\mathrm {at}^\mathrm {Pair})^\times )$. Let ![]() $\mathbf {X}^\otimes \in \mathrm {CAlg}(2\text {-}\mathcal {C}\mathrm {at}^\times )$. Then for any symmetric monoidal functor
$\mathbf {X}^\otimes \in \mathrm {CAlg}(2\text {-}\mathcal {C}\mathrm {at}^\times )$. Then for any symmetric monoidal functor ![]() $\Phi : \mathbf {C}\to \mathbf {X}$ that is left-adjointable with respect to
$\Phi : \mathbf {C}\to \mathbf {X}$ that is left-adjointable with respect to ![]() $\mathcal {D}$ (as a plain functor), it extends uniquely to a symmetric monoidal functor
$\mathcal {D}$ (as a plain functor), it extends uniquely to a symmetric monoidal functor
in ![]() $\mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}}$.
$\mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}}$.
Proof. First, both the functors ![]() $\mathrm {Sq}_{\bullet, \bullet }^{\tilde {}}: 2\text {-}\mathcal {C}\mathrm {at}\to \mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}}$ and
$\mathrm {Sq}_{\bullet, \bullet }^{\tilde {}}: 2\text {-}\mathcal {C}\mathrm {at}\to \mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}}$ and ![]() $\mathrm {Sq}_{\bullet,\bullet }^{\mathrm {Pair}}: 2\text {-}\mathcal {C}\mathrm {at}^{\mathrm {Pair}}\to \mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}}$ are fully faithful symmetric monoidal functors. The full faithfulness follows from [Reference Gaitsgory and RozenblyumGR17, Chapter 10, 2.6.1Footnote 11, Theorem 4.3.5]), and the symmetric monoidal structure follows from definition. Since
$\mathrm {Sq}_{\bullet,\bullet }^{\mathrm {Pair}}: 2\text {-}\mathcal {C}\mathrm {at}^{\mathrm {Pair}}\to \mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}}$ are fully faithful symmetric monoidal functors. The full faithfulness follows from [Reference Gaitsgory and RozenblyumGR17, Chapter 10, 2.6.1Footnote 11, Theorem 4.3.5]), and the symmetric monoidal structure follows from definition. Since
for any ![]() $\mathbf {C}'\in 2\text {-}\mathcal {C}\mathrm {at}$. We see that (A.3.2) for the given
$\mathbf {C}'\in 2\text {-}\mathcal {C}\mathrm {at}$. We see that (A.3.2) for the given ![]() $(\mathbf {C}^{\otimes }, \mathcal {D})$ is a symmetric monoidal bi-simplicial functor.
$(\mathbf {C}^{\otimes }, \mathcal {D})$ is a symmetric monoidal bi-simplicial functor.
Second, by Theorem A.16 and that all functors respect the Cartesian products, we know that for any ![]() $n\in \mathbf {Z}_{\geq 0}$
$n\in \mathbf {Z}_{\geq 0}$
is a categorical epimorphism with respect to the essential image of ![]() $\mathrm {Sq}_{\bullet,\bullet }$. Hence, by (an obvious generalization of) [Reference Gaitsgory and RozenblyumGR17, Chapter 9, Lemma 3.1.3], restricting along (A.3.2) defines an isomorphism between the space of symmetric monoidal functors from
$\mathrm {Sq}_{\bullet,\bullet }$. Hence, by (an obvious generalization of) [Reference Gaitsgory and RozenblyumGR17, Chapter 9, Lemma 3.1.3], restricting along (A.3.2) defines an isomorphism between the space of symmetric monoidal functors from ![]() $\mathrm {Sq}^{\mathrm {Pair}}_{\bullet, \bullet }(\mathbf {C}^{2\text {-}{\rm op}}, \mathcal {D})^{\mathrm {vert}\text {-}\mathrm {op}}$ to
$\mathrm {Sq}^{\mathrm {Pair}}_{\bullet, \bullet }(\mathbf {C}^{2\text {-}{\rm op}}, \mathcal {D})^{\mathrm {vert}\text {-}\mathrm {op}}$ to ![]() $\mathrm {Sq}_{\bullet,\bullet }\mathbf {X}$ and the space of symmetric monoidal functors from
$\mathrm {Sq}_{\bullet,\bullet }\mathbf {X}$ and the space of symmetric monoidal functors from ![]() $\mathbf {C}$ to
$\mathbf {C}$ to ![]() $\mathbf {X}$ that factors through
$\mathbf {X}$ that factors through ![]() $\mathbf {C}^{R_\mathcal {D}}$ as a plain functor. However, the latter space is exactly the subspace consisting of left-adjointable functors with respect to
$\mathbf {C}^{R_\mathcal {D}}$ as a plain functor. However, the latter space is exactly the subspace consisting of left-adjointable functors with respect to ![]() $\mathcal {D}$.
$\mathcal {D}$.
By definition, we have a symmetric monoidal functor ![]() $(\mathrm {VTop}, \mathsf {propfib}')\to (\mathcal {V}\mathcal {S}\mathrm {pc},\mathsf {hpf}')$ in
$(\mathrm {VTop}, \mathsf {propfib}')\to (\mathcal {V}\mathcal {S}\mathrm {pc},\mathsf {hpf}')$ in ![]() $2\text {-}\mathcal {C}\mathrm {at}^{\mathrm {Pair}}$.
$2\text {-}\mathcal {C}\mathrm {at}^{\mathrm {Pair}}$.
Corollary A.18 There is a canonical commutative diagram in ![]() $\mathrm {CAlg}((\mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}})^{\times })$
$\mathrm {CAlg}((\mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}})^{\times })$

where the vertical functor is induced from localization, and the horizontal and slant functors are determined by ![]() $\mathbb {T}_{\mathrm {VTop}}$ and
$\mathbb {T}_{\mathrm {VTop}}$ and ![]() $\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}$, respectively (up to a contractible space of choices).
$\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}$, respectively (up to a contractible space of choices).
Proof. Consider the following commutative diagram in ![]() $\mathrm {CAlg}((1\text {-}\mathcal {C}\mathrm {at}^\mathrm {Pair})^\times )$.
$\mathrm {CAlg}((1\text {-}\mathcal {C}\mathrm {at}^\mathrm {Pair})^\times )$.

Applying ![]() $\mathrm {Sq}_{\bullet, \bullet }^\mathrm {Pair}((-)^{\rm op},(-)^{\rm op})^{\mathrm {vert}\text {-}\mathrm {op}}$, we get a commutative diagram in
$\mathrm {Sq}_{\bullet, \bullet }^\mathrm {Pair}((-)^{\rm op},(-)^{\rm op})^{\mathrm {vert}\text {-}\mathrm {op}}$, we get a commutative diagram in ![]() $\mathrm {CAlg}((\mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}})^\times )$, where all the morphisms are categorical epimorphisms with respect to the essential image of
$\mathrm {CAlg}((\mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}})^\times )$, where all the morphisms are categorical epimorphisms with respect to the essential image of ![]() $\mathrm {Sq}_{\bullet,\bullet }$. Indeed, for the horizontal morphisms, this follows from Theorem A.16 again, and for the vertical morphisms, this follows the universal property of localizations.
$\mathrm {Sq}_{\bullet,\bullet }$. Indeed, for the horizontal morphisms, this follows from Theorem A.16 again, and for the vertical morphisms, this follows the universal property of localizations.
Now by Corollaries A.12, A.14, and A.17 (and a similar argument for it), we get ![]() $\mathbb {T}_{\mathrm {VTop}}$ determines the following unique commutative diagram in
$\mathbb {T}_{\mathrm {VTop}}$ determines the following unique commutative diagram in ![]() $\mathrm {CAlg}((\mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}})^\times )$.
$\mathrm {CAlg}((\mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}})^\times )$.

In particular, we get (A.3.3) with the prescribed property.
A.3.2 The bi-simplicial space of grids with defect and symmetric monoidal upgrades
Recall the bi-simplicial space of grids with defect from [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 2.1]. For any ![]() $(\infty,1)$-category
$(\infty,1)$-category ![]() $\mathcal {C}$ and classes
$\mathcal {C}$ and classes ![]() $(vert, horiz, adm)$. let
$(vert, horiz, adm)$. let ![]() $\mathrm {defGrid}_{\bullet, \bullet }(\mathcal {C})^{adm}_{vert, horiz}\in \mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}}$ defined as
$\mathrm {defGrid}_{\bullet, \bullet }(\mathcal {C})^{adm}_{vert, horiz}\in \mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}}$ defined as ![]() $\mathrm {defGrid}_{m,n}(\mathcal {C})^{adm}_{vert, horiz}$ is the full subspace of
$\mathrm {defGrid}_{m,n}(\mathcal {C})^{adm}_{vert, horiz}$ is the full subspace of ![]() $\mathrm {Maps}([m]\times [n]^{\rm op}, \mathcal {C})$ consisting of objects
$\mathrm {Maps}([m]\times [n]^{\rm op}, \mathcal {C})$ consisting of objects ![]() $\underline {\mathbf {c}}$ with the following properties:
$\underline {\mathbf {c}}$ with the following properties:
(1) for any
 $0\leq i< i+1\leq m$, the map
$0\leq i< i+1\leq m$, the map  $\mathbf {c}_{i,j}\to \mathbf {c}_{i+1, j}$ belongs to
$\mathbf {c}_{i,j}\to \mathbf {c}_{i+1, j}$ belongs to  $vert$;
$vert$;(2) for any
 $0\leq j-1< j\leq n$, the map
$0\leq j-1< j\leq n$, the map  $\mathbf {c}_{i,j}\to \mathbf {c}_{i,j-1}$ belongs to
$\mathbf {c}_{i,j}\to \mathbf {c}_{i,j-1}$ belongs to  $horiz$;
$horiz$;(3) for any
 $0\leq i< i+1\leq m$ and
$0\leq i< i+1\leq m$ and  $0\leq j-1< j\leq n$ in the commutative square
its defect of Cartesianness, i.e. the map
$0\leq j-1< j\leq n$ in the commutative square
its defect of Cartesianness, i.e. the map
 $\mathbf {c}_{i,j}\to \mathbf {c}_{i+1,j}\underset {\mathbf {c}_{i+1, j-1}}{\times }\mathbf {c}_{i,j-1}$ belongs to
$\mathbf {c}_{i,j}\to \mathbf {c}_{i+1,j}\underset {\mathbf {c}_{i+1, j-1}}{\times }\mathbf {c}_{i,j-1}$ belongs to  $adm$.
$adm$.
It is shown in [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 2.1.2, 2.3] that there is a canonical map in ![]() $\mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}}$
$\mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}}$
whose key feature is stated in [Reference Gaitsgory and RozenblyumGR17, Chapter 7, Theorem 2.1.3]. The map is explicitly given by the composition
followed by the map
To define the functor (A.3.5), one introduces for each ![]() $n$, a 1-full subcategory of
$n$, a 1-full subcategory of ![]() ${\mathcal {M} \text{aps}}([n]^{\rm op}, \mathcal {C})$, denoted by
${\mathcal {M} \text{aps}}([n]^{\rm op}, \mathcal {C})$, denoted by ![]() ${\mathcal {M} \text{aps}}([n]^{\rm op}, \mathcal {C})_{vert, horiz}^{adm}$. We refer the reader to [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 2.3.2] for its definition. The upshot is there is a canonical isomorphism of bi-simplicial spaces
${\mathcal {M} \text{aps}}([n]^{\rm op}, \mathcal {C})_{vert, horiz}^{adm}$. We refer the reader to [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 2.3.2] for its definition. The upshot is there is a canonical isomorphism of bi-simplicial spaces
and there is a canonically defined fully faithful embedding
that sends every ![]() $\bullet$-string in
$\bullet$-string in ![]() $\mathcal {C}$ to the half grids with all vertical maps isomorphisms.
$\mathcal {C}$ to the half grids with all vertical maps isomorphisms.
Lemma A.19 Assume ![]() $\mathcal {C}\in \mathrm {CAlg}(1\text {-}\mathcal {C}\mathrm {at}^\times )$, and the classes of morphisms
$\mathcal {C}\in \mathrm {CAlg}(1\text {-}\mathcal {C}\mathrm {at}^\times )$, and the classes of morphisms ![]() $vert, horiz, adm$ in
$vert, horiz, adm$ in ![]() $\mathcal {C}$ are closed under the tensor product. Then we get a natural commutative diagram in
$\mathcal {C}$ are closed under the tensor product. Then we get a natural commutative diagram in ![]() $\mathrm {CAlg}(1\text {-}\mathcal {C}\mathrm {at}^\times )$:
$\mathrm {CAlg}(1\text {-}\mathcal {C}\mathrm {at}^\times )$:

where the symmetric monoidal structure on the left-hand side (respectively, right-hand side) are those induced from ![]() $\mathrm {Corr}(\mathcal {C})^{adm}_{vert, horiz}$ (respectively,
$\mathrm {Corr}(\mathcal {C})^{adm}_{vert, horiz}$ (respectively, ![]() $\mathrm {Fun}(([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C})$).
$\mathrm {Fun}(([n]\times [n]^{\rm op})^{\geq \mathrm {dgnl}}, \mathcal {C})$).
Proof. The proof follows directly from [Reference Gaitsgory and RozenblyumGR17, Chapter 9, 2.1; Chapter 7, 1.4]. Let ![]() $\mathrm {Trpl}$ be the
$\mathrm {Trpl}$ be the ![]() $(\infty,1)$-category consisting of objects
$(\infty,1)$-category consisting of objects ![]() $(\mathcal {C}; vert, horiz, adm)$ as in [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 1.1] and the space of morphisms between two objects consisting of the full subspace of functors between the
$(\mathcal {C}; vert, horiz, adm)$ as in [Reference Gaitsgory and RozenblyumGR17, Chapter 7, 1.1] and the space of morphisms between two objects consisting of the full subspace of functors between the ![]() $\mathcal {C}$-variables that preserves the three classes of morphisms and Cartesian squares from[Reference Gaitsgory and RozenblyumGR17, Chapter 7, 1.1]. Consider the following diagram:
$\mathcal {C}$-variables that preserves the three classes of morphisms and Cartesian squares from[Reference Gaitsgory and RozenblyumGR17, Chapter 7, 1.1]. Consider the following diagram:

in which the functors are given by the assignments
 \begin{align*} &\mathrm{Corr}:
(\mathcal{C}; vert, horiz, adm)\mapsto
\mathrm{Corr}(\mathcal{C})_{vert, horiz}^{adm},\\
&\mathrm{Corr}^{\mathrm{Pair}}: (\mathcal{C}; vert, horiz,
adm)\mapsto (\mathrm{Corr}(\mathcal{C})_{vert,
horiz}^{adm},\mathcal{C}_{vert}),\\ & {''}{\mathrm{Grid}_\bullet^{\geq\mathrm{dgnl}}}{}:
(\mathcal{C}; vert, horiz,
adm)\mapsto{''}{\mathrm{Grid}_\bullet^{\geq\mathrm{dgnl}}(\mathcal{C})}{}_{vert,
horiz}^{adm},\\
&\mathrm{Grid}_\bullet^{\geq\mathrm{dgnl}}: (\mathcal{C};
vert, horiz, adm)\mapsto
\mathrm{Grid}_\bullet^{\geq\mathrm{dgnl}}(\mathcal{C})_{vert,
horiz}^{adm}. \end{align*}
\begin{align*} &\mathrm{Corr}:
(\mathcal{C}; vert, horiz, adm)\mapsto
\mathrm{Corr}(\mathcal{C})_{vert, horiz}^{adm},\\
&\mathrm{Corr}^{\mathrm{Pair}}: (\mathcal{C}; vert, horiz,
adm)\mapsto (\mathrm{Corr}(\mathcal{C})_{vert,
horiz}^{adm},\mathcal{C}_{vert}),\\ & {''}{\mathrm{Grid}_\bullet^{\geq\mathrm{dgnl}}}{}:
(\mathcal{C}; vert, horiz,
adm)\mapsto{''}{\mathrm{Grid}_\bullet^{\geq\mathrm{dgnl}}(\mathcal{C})}{}_{vert,
horiz}^{adm},\\
&\mathrm{Grid}_\bullet^{\geq\mathrm{dgnl}}: (\mathcal{C};
vert, horiz, adm)\mapsto
\mathrm{Grid}_\bullet^{\geq\mathrm{dgnl}}(\mathcal{C})_{vert,
horiz}^{adm}. \end{align*}
and the natural transformations marked are the obvious ones. Moreover, the same diagram has the following features:
– all functors are symmetric monoidal with respect to the Cartesian symmetric monoidal structures on the categories, and both natural transformations are between the symmetric monoidal functors;
– except for the double arrows, all three solid faces are commutative, with functors in gray located at the ‘back’;
– the natural transformation
 ${''}{\mathrm {Grid}_\bullet ^{\geq \mathrm {dgnl}}(\mathcal {C})}{}_{vert, horiz}^{adm}\to {\mathrm {Grid}_\bullet ^{\geq \mathrm {dgnl}}(\mathcal {C})}_{vert, horiz}^{adm}$ is just the pullback of the other natural transformation along
${''}{\mathrm {Grid}_\bullet ^{\geq \mathrm {dgnl}}(\mathcal {C})}{}_{vert, horiz}^{adm}\to {\mathrm {Grid}_\bullet ^{\geq \mathrm {dgnl}}(\mathcal {C})}_{vert, horiz}^{adm}$ is just the pullback of the other natural transformation along  $\mathrm {Corr}^{\mathrm {Pair}}$ (and using the two solid triangles containing them).
$\mathrm {Corr}^{\mathrm {Pair}}$ (and using the two solid triangles containing them).
Then the diagram (A.3.8) is obtained from applying the functors and natural transformations to ![]() $(\mathcal {C};vert, horiz, adm)$ in the obvious way.
$(\mathcal {C};vert, horiz, adm)$ in the obvious way.
Corollary A.20 Under the same assumption as in Lemma A.19, the map (A.3.4) is naturally symmetric monoidal and is a categorical epimorphism with respect to the essential image of ![]() $\mathrm {Sq}_{\bullet, \bullet }$.
$\mathrm {Sq}_{\bullet, \bullet }$.
Proof. Since (A.3.5) and (A.3.6) are both symmetric monoidal (using Lemma A.19), (A.3.4) is symmetric monoidal as the composition. The last part follows from the key feature of the map (A.3.4) [Reference Gaitsgory and RozenblyumGR17, Chapter 7, Theorem 2.1.3].
We immediately get a symmetric monoidal version of [Reference Gaitsgory and RozenblyumGR17, Chapter 7, Theorem 2.1.3].
Corollary A.21 Under the same assumption as in Lemma A.19, for any symmetric monoidal ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\mathbf {X}$, the symmetric monoidal functor (A.3.4) defines an isomorphism between the space of symmetric monoidal functors
$\mathbf {X}$, the symmetric monoidal functor (A.3.4) defines an isomorphism between the space of symmetric monoidal functors ![]() $\mathrm {Corr}(\mathcal {C})_{vert, horiz}^{adm}\to \mathbf {X}$ and the subspace of bi-simplicial symmetric monoidal functors
$\mathrm {Corr}(\mathcal {C})_{vert, horiz}^{adm}\to \mathbf {X}$ and the subspace of bi-simplicial symmetric monoidal functors
with the following property: for every ![]() $\underline {c}\in \mathrm {defGrid}_{1,1}(\mathcal {C})_{vert, horiz}^{adm}$, such that the diagram
$\underline {c}\in \mathrm {defGrid}_{1,1}(\mathcal {C})_{vert, horiz}^{adm}$, such that the diagram

is Cartesian, the corresponding object

in ![]() $\mathrm {Sq}_{1,1}(\mathbf {X})$ represents an invertible 2-morphism.
$\mathrm {Sq}_{1,1}(\mathbf {X})$ represents an invertible 2-morphism.
A.3.3
Consider the following commutative diagram in ![]() $\mathrm {CAlg}(\mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}})$:
$\mathrm {CAlg}(\mathcal {S}\mathrm {pc}^{\Delta ^{\rm op}\times \Delta ^{\rm op}})$:

where the horizontal maps are induced from the tautological functor ![]() $[m]{\bigcirc{\kern-6pt \star}}[n]=:[m,n]\to [m]\times [n]$ (similarly to the definition of [Reference Gaitsgory and RozenblyumGR17, Chapter 7, (3.3)]).
$[m]{\bigcirc{\kern-6pt \star}}[n]=:[m,n]\to [m]\times [n]$ (similarly to the definition of [Reference Gaitsgory and RozenblyumGR17, Chapter 7, (3.3)]).
Proposition A.22 There is a natural commutative diagram in ![]() $\mathrm {CAlg}(2\text {-}\mathcal {C}\mathrm {at}^\times )$:
$\mathrm {CAlg}(2\text {-}\mathcal {C}\mathrm {at}^\times )$:

where:
– the functors in the leftmost column are the localization (top) and the 1-full embedding (bottom);
–
 $\mathbb {T}_{\mathrm {VTop}}^{\mathrm {Corr}}|_{\mathrm {VTop}^{\rm op}}\cong \mathbb {T}_{\mathrm {VTop}}$,
$\mathbb {T}_{\mathrm {VTop}}^{\mathrm {Corr}}|_{\mathrm {VTop}^{\rm op}}\cong \mathbb {T}_{\mathrm {VTop}}$,  $\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}^{\mathrm {Corr}}|_{\mathcal {V}\mathcal {S}\mathrm {pc}^{\rm op}}\cong \mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}$, and
$\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}^{\mathrm {Corr}}|_{\mathcal {V}\mathcal {S}\mathrm {pc}^{\rm op}}\cong \mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}$, and  $\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}_{\mathsf {hpf}'}}^{\mathrm {Corr}}=\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}^{\mathrm {Corr}}|_{\mathrm {Corr}(\mathcal {V}\mathcal {S}\mathrm {pc})_{\mathsf {hpf}', \mathsf {hpf}'}}$.
$\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}_{\mathsf {hpf}'}}^{\mathrm {Corr}}=\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}^{\mathrm {Corr}}|_{\mathrm {Corr}(\mathcal {V}\mathcal {S}\mathrm {pc})_{\mathsf {hpf}', \mathsf {hpf}'}}$.
A.4 Proof of Proposition 4.13 (the equivalent model of  $J$)
$J$)
We will need the following to connect ![]() $\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}(p:VG\to G)$ with
$\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}(p:VG\to G)$ with ![]() $(p_*\varpi _{VG}\in \mathrm {Loc}(G;\mathrm {Sp})^{\otimes _c})$. An object in
$(p_*\varpi _{VG}\in \mathrm {Loc}(G;\mathrm {Sp})^{\otimes _c})$. An object in ![]() $\mathrm {CAlg}((\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}//})$ is equivalent to the datum of a commutative diagram
$\mathrm {CAlg}((\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}//})$ is equivalent to the datum of a commutative diagram

whose restriction to ![]() $N(\mathrm {Fin}_*){\bigcirc{\kern-6pt \star}}\Delta ^{\{0\}}\simeq N(\mathrm {Fin}_*)$ (respectively,
$N(\mathrm {Fin}_*){\bigcirc{\kern-6pt \star}}\Delta ^{\{0\}}\simeq N(\mathrm {Fin}_*)$ (respectively, ![]() $N(\mathrm {Fin}_*){\bigcirc{\kern-6pt \star}}\Delta ^{\{1\}}$) gives the monoidal unit
$N(\mathrm {Fin}_*){\bigcirc{\kern-6pt \star}}\Delta ^{\{1\}}$) gives the monoidal unit ![]() $\mathrm {Sp}$ (respectively, an algebra
$\mathrm {Sp}$ (respectively, an algebra ![]() $C\in \mathrm {CAlg}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$). Passing to
$C\in \mathrm {CAlg}(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})$). Passing to ![]() $1\& 2\text {-}\mathrm {op}$, the diagram becomes
$1\& 2\text {-}\mathrm {op}$, the diagram becomes

where the right vertical functor is the 2-Cartesian fibration representing the symmetric monoidal structure on ![]() $\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}}$. Assuming the horizontal arrows in the second factor
$\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}}$. Assuming the horizontal arrows in the second factor ![]() $\Delta ^1$ (i.e.
$\Delta ^1$ (i.e. ![]() $\{\langle n\rangle \}\times \Delta ^1$) of (
$\{\langle n\rangle \}\times \Delta ^1$) of (
) also admit left adjoints, then we can use [Reference Gaitsgory and RozenblyumGR17, Chapter 12, Corollary 3.1.7] to (canonically) transform the diagram into

by passing to the left adjoints for morphisms from the factor ![]() $(\Delta ^1)^{\rm op}\simeq \Delta ^1$, which gives a corresponding object in
$(\Delta ^1)^{\rm op}\simeq \Delta ^1$, which gives a corresponding object in ![]() $\mathrm {CcoAlg}(((\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}})^{2\text {-}{\rm op}})^{\mathrm {Sp}/ /})$, where
$\mathrm {CcoAlg}(((\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}})^{2\text {-}{\rm op}})^{\mathrm {Sp}/ /})$, where ![]() $\mathrm {CcoAlg}$ means the
$\mathrm {CcoAlg}$ means the ![]() $(\infty,1)$-category of commutative coalgebras. The above correspondence clearly upgrades to the following.
$(\infty,1)$-category of commutative coalgebras. The above correspondence clearly upgrades to the following.
Lemma A.23 There is a natural commutative diagram

where the vertical isomorphisms are the tautological ones, and the subscript ![]() $\mathcal {R}$ (respectively,
$\mathcal {R}$ (respectively, ![]() $\mathcal {L}$) means the full subspace consisting of objects with the horizontal (respectively, vertical) arrows in (A.4.1) (respectively, (A.4.2)) admitting left adjoints (respectively, right adjoints) in the fibers of the 2-coCartesian (respectively, 2-Cartesian) fibrations.
$\mathcal {L}$) means the full subspace consisting of objects with the horizontal (respectively, vertical) arrows in (A.4.1) (respectively, (A.4.2)) admitting left adjoints (respectively, right adjoints) in the fibers of the 2-coCartesian (respectively, 2-Cartesian) fibrations.
Let ![]() $\mathrm {Sp}_{\mathsf {perf}}$ be the full subcategory of
$\mathrm {Sp}_{\mathsf {perf}}$ be the full subcategory of ![]() $\mathrm {Sp}$ consisting of perfect
$\mathrm {Sp}$ consisting of perfect ![]() $\mathbf {S}$-modules.
$\mathbf {S}$-modules.
Corollary A.24 For any ![]() $K\in \mathrm {CAlg}(\mathcal {S}\mathrm {pc}^\times )$, there is a natural isomorphism
$K\in \mathrm {CAlg}(\mathcal {S}\mathrm {pc}^\times )$, there is a natural isomorphism
where ![]() $\mathrm {CAlg}((\mathrm {Loc}(K;\mathrm {Sp})^{\otimes _c})_{\mathsf {perf}}$ is the full subcategory of
$\mathrm {CAlg}((\mathrm {Loc}(K;\mathrm {Sp})^{\otimes _c})_{\mathsf {perf}}$ is the full subcategory of ![]() $\mathrm {CAlg}((\mathrm {Loc}(K;\mathrm {Sp}))^{\otimes _c}$ whose underlying local systems have perfect costalks.
$\mathrm {CAlg}((\mathrm {Loc}(K;\mathrm {Sp}))^{\otimes _c}$ whose underlying local systems have perfect costalks.
Proof. Using Lemma A.23, we just need to examine the space of diagrams (A.4.2) whose restriction at ![]() $\{0\}\times N(\mathrm {Fin}_*)^{\rm op}$ and
$\{0\}\times N(\mathrm {Fin}_*)^{\rm op}$ and ![]() $\{1\}\times N(\mathrm {Fin}_*)^{\rm op}$ give the structure of
$\{1\}\times N(\mathrm {Fin}_*)^{\rm op}$ give the structure of ![]() $\mathrm {Sp}$ and
$\mathrm {Sp}$ and ![]() $\mathrm {Loc}(K;\mathrm {Sp})\simeq \mathrm {Fun}(K;\mathrm {Sp})$ as commutative coalgebra objects in
$\mathrm {Loc}(K;\mathrm {Sp})\simeq \mathrm {Fun}(K;\mathrm {Sp})$ as commutative coalgebra objects in ![]() $\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}}$, and then restrict to local systems with perfect costalks. Unwinding the data of the diagram, one sees exactly the data of a right-lax homomorphism from
$\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}}$, and then restrict to local systems with perfect costalks. Unwinding the data of the diagram, one sees exactly the data of a right-lax homomorphism from ![]() $K$ to
$K$ to ![]() $\mathrm {Sp}_\mathsf {perf}$. For example, for the unique active map
$\mathrm {Sp}_\mathsf {perf}$. For example, for the unique active map ![]() $\alpha : \langle 1\rangle \leftarrow \langle 2\rangle$ in
$\alpha : \langle 1\rangle \leftarrow \langle 2\rangle$ in ![]() $N(\mathrm {Fin}_*)$, the horizontal arrow in (A.4.2) sends
$N(\mathrm {Fin}_*)$, the horizontal arrow in (A.4.2) sends ![]() $\Delta ^1{\bigcirc{\kern-6pt \star}} \alpha^{\textrm {op}}\simeq (\alpha ^{\textrm {op}}{\bigcirc{\kern-6pt \star}} \Delta ^1)^{2\textrm {-}\textrm {op}}$ to
$\Delta ^1{\bigcirc{\kern-6pt \star}} \alpha^{\textrm {op}}\simeq (\alpha ^{\textrm {op}}{\bigcirc{\kern-6pt \star}} \Delta ^1)^{2\textrm {-}\textrm {op}}$ to

in which the bottom functor is determined by a local system with perfect costalks, the upper square with squiggly vertical arrows represents a 2-Cartesian morphism in ![]() $\mathrm {Fun}(\Delta ^1, (\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}})^{\otimes, \mathrm {Fin}_*^{\rm op}})$ over
$\mathrm {Fun}(\Delta ^1, (\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}})^{\otimes, \mathrm {Fin}_*^{\rm op}})$ over ![]() $\alpha ^{\rm op}\in \mathrm {Fun}(\Delta ^1, N(\mathrm {Fin}_*)^{\rm op})$ and
$\alpha ^{\rm op}\in \mathrm {Fun}(\Delta ^1, N(\mathrm {Fin}_*)^{\rm op})$ and ![]() $m: K\times K\to K$ is the multiplication map determined by the functor
$m: K\times K\to K$ is the multiplication map determined by the functor ![]() $N(\mathrm {Fin}_*)\to 1\text {-}\mathcal {C}\mathrm {at}$ (and essentially determined by the image of
$N(\mathrm {Fin}_*)\to 1\text {-}\mathcal {C}\mathrm {at}$ (and essentially determined by the image of ![]() $\alpha$) representing
$\alpha$) representing ![]() $K\in \mathrm {CAlg}(1\text {-}\mathcal {C}\mathrm {at})$. Then the bottom square in
$K\in \mathrm {CAlg}(1\text {-}\mathcal {C}\mathrm {at})$. Then the bottom square in ![]() $\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}}$ encodes exactly a diagram
$\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}}$ encodes exactly a diagram ![]() $\Delta ^1{\bigcirc{\kern-6pt \star}} \Delta ^1\to \mathbf {1}\textrm {-}\mathcal {C}\mathbf {at}$:
$\Delta ^1{\bigcirc{\kern-6pt \star}} \Delta ^1\to \mathbf {1}\textrm {-}\mathcal {C}\mathbf {at}$:

Examining through all the ![]() $n$-simplices in
$n$-simplices in ![]() $N(\mathrm {Fin}_*)^{\rm op}$ and their obvious compatibility (as encoded in
$N(\mathrm {Fin}_*)^{\rm op}$ and their obvious compatibility (as encoded in ![]() $\mathrm {Seq}_\bullet N(\mathrm {Fin}_*)^{\rm op}$), gives the corresponding right-lax homomorphism
$\mathrm {Seq}_\bullet N(\mathrm {Fin}_*)^{\rm op}$), gives the corresponding right-lax homomorphism ![]() $K\to \mathrm {Sp}_{\mathsf {perf}}$ encoded by a functor
$K\to \mathrm {Sp}_{\mathsf {perf}}$ encoded by a functor ![]() $N(\mathrm {Fin}_*){\bigcirc{\kern-6pt \star}} \Delta ^1\to \mathbf {1}\textrm {-}\mathcal {C}\mathbf {at}$. The assignment is certainly functorial in any diagram (A.4.2) parametrized by a simplex, i.e. replacing the source
$N(\mathrm {Fin}_*){\bigcirc{\kern-6pt \star}} \Delta ^1\to \mathbf {1}\textrm {-}\mathcal {C}\mathbf {at}$. The assignment is certainly functorial in any diagram (A.4.2) parametrized by a simplex, i.e. replacing the source ![]() $\Delta ^1 {\bigcirc{\kern-6pt \star}} N(\mathrm {Fin}_*)^{\textrm {op}}$ by
$\Delta ^1 {\bigcirc{\kern-6pt \star}} N(\mathrm {Fin}_*)^{\textrm {op}}$ by ![]() $\Delta ^n\times ( \Delta ^1 {\bigcirc{\kern-6pt \star}} N(\mathrm {Fin}_*)^{\textrm {op}})$, hence leading to the isomorphism (A.4.4).
$\Delta ^n\times ( \Delta ^1 {\bigcirc{\kern-6pt \star}} N(\mathrm {Fin}_*)^{\textrm {op}})$, hence leading to the isomorphism (A.4.4).
Proof of Proposition 4.13 We prove the proposition in the following steps.
Step 1: the homomorphisms ![]() $(p_{\hat {N}}: VG_{\hat {N}}\to G_{\hat {N}})\to (p_{\hat {M}}: VG_{\hat {M}}\to G_{\hat {M}}), \hat {N}\in \mathbf {Z}_{\geq 0}\cup \{+\infty \}$ in
$(p_{\hat {N}}: VG_{\hat {N}}\to G_{\hat {N}})\to (p_{\hat {M}}: VG_{\hat {M}}\to G_{\hat {M}}), \hat {N}\in \mathbf {Z}_{\geq 0}\cup \{+\infty \}$ in ![]() $\mathrm {CAlg}(\mathrm {Corr}(\mathrm {VTop})_{\mathsf {propfib}', \mathsf {all}})$. Here when
$\mathrm {CAlg}(\mathrm {Corr}(\mathrm {VTop})_{\mathsf {propfib}', \mathsf {all}})$. Here when ![]() $\hat {N}=+\infty$,
$\hat {N}=+\infty$, ![]() $p_{+\infty }$ means
$p_{+\infty }$ means ![]() $(p: VG\to G)$. First, using Theorem 2.8(ii),
$(p: VG\to G)$. First, using Theorem 2.8(ii), ![]() $(p^\bullet :VG^\bullet \to G^\bullet )$ and
$(p^\bullet :VG^\bullet \to G^\bullet )$ and ![]() $(p_N^\bullet : VG_N^\bullet \to G_N^\bullet )$ give commutative algebra objects in
$(p_N^\bullet : VG_N^\bullet \to G_N^\bullet )$ give commutative algebra objects in ![]() $\mathrm {Corr}(\mathrm {Fun}(\Delta ^1, \mathrm {Top}))$. Using the proof of Theorem 2.8 and that all vertical morphisms (corresponding to active morphisms in
$\mathrm {Corr}(\mathrm {Fun}(\Delta ^1, \mathrm {Top}))$. Using the proof of Theorem 2.8 and that all vertical morphisms (corresponding to active morphisms in ![]() $N(\mathrm {Fin}_*)$) are proper locally trivial fibrations (note that the fibrations are usually not surjective on the components of the base), we see that
$N(\mathrm {Fin}_*)$) are proper locally trivial fibrations (note that the fibrations are usually not surjective on the components of the base), we see that ![]() $(p^\bullet :VG^\bullet \to G^\bullet )$ and
$(p^\bullet :VG^\bullet \to G^\bullet )$ and ![]() $(p_N^\bullet : VG_N^\bullet \to G_N^\bullet )$ give commutative algebra objects in the 1-full symmetric monoidal subcategory
$(p_N^\bullet : VG_N^\bullet \to G_N^\bullet )$ give commutative algebra objects in the 1-full symmetric monoidal subcategory ![]() $\mathrm {Corr}(\mathrm {VTop})_{\mathsf {propfib}', \mathsf {all}}$. We remark that this further uses that for every active map
$\mathrm {Corr}(\mathrm {VTop})_{\mathsf {propfib}', \mathsf {all}}$. We remark that this further uses that for every active map ![]() $\langle n\rangle \to \langle m\rangle$, the Cartesian square
$\langle n\rangle \to \langle m\rangle$, the Cartesian square

represents a morphism in ![]() $\mathrm {VTop}$.
$\mathrm {VTop}$.
The claim about the homomorphism follows from applying Theorem 2.13 and a similar consideration as above.
Step 2: the equivalence
in ![]() $\mathrm {CAlg}((\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}/})$. Applying
$\mathrm {CAlg}((\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}/})$. Applying ![]() $\mathbb {T}_{\mathrm {VTop}}^{\mathrm {Corr}}$ to the homomorphisms from Step 1, we get a natural functor (A.4.5). The functor is an equivalence, which follows from the assertion on
$\mathbb {T}_{\mathrm {VTop}}^{\mathrm {Corr}}$ to the homomorphisms from Step 1, we get a natural functor (A.4.5). The functor is an equivalence, which follows from the assertion on ![]() $\mathbb {T}_{\mathrm {VTop}}$ (see the proof of Proposition A.12).
$\mathbb {T}_{\mathrm {VTop}}$ (see the proof of Proposition A.12).
Step 3: ![]() $\mathbb {T}_{\mathrm {VTop}}^{\mathrm {Corr}}(p_N:VG_N\to G_N)$ is isomorphic to
$\mathbb {T}_{\mathrm {VTop}}^{\mathrm {Corr}}(p_N:VG_N\to G_N)$ is isomorphic to ![]() $(\mathrm {Loc}(G_N;\mathrm {Sp})^{\otimes _c}\ni (p_N)_*\varpi _{VG_N})$. Recall
$(\mathrm {Loc}(G_N;\mathrm {Sp})^{\otimes _c}\ni (p_N)_*\varpi _{VG_N})$. Recall ![]() $\mathrm {Loc}(G_N;\mathrm {Sp})^{\otimes _c}\ni (p_N)_*\varpi _{VG_N}$ is obtained using the correspondence
$\mathrm {Loc}(G_N;\mathrm {Sp})^{\otimes _c}\ni (p_N)_*\varpi _{VG_N}$ is obtained using the correspondence

interpreted as a right-lax homomorphism from ![]() $pt$ to
$pt$ to ![]() $G_N$ in
$G_N$ in ![]() $\mathbf {Corr}(\mathrm {S}_{\mathrm {LCH}})$ by Theorem 2.13. By Proposition A.4, this right-lax homomorphism is the same as the image of
$\mathbf {Corr}(\mathrm {S}_{\mathrm {LCH}})$ by Theorem 2.13. By Proposition A.4, this right-lax homomorphism is the same as the image of ![]() $VG_N^\bullet \to G_N^\bullet$ (as an object in
$VG_N^\bullet \to G_N^\bullet$ (as an object in ![]() $\mathrm {CAlg}(\mathrm {Corr}(\mathrm {V}\mathrm {S}_{\mathrm {LCH}})_{\mathsf {propfib}', \mathsf {all}})$) in
$\mathrm {CAlg}(\mathrm {Corr}(\mathrm {V}\mathrm {S}_{\mathrm {LCH}})_{\mathsf {propfib}', \mathsf {all}})$) in ![]() $\mathrm {CAlg}(\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {propfib},\mathsf {all}}^{pt//})$. Hence, the claimed isomorphism follows.
$\mathrm {CAlg}(\mathrm {Corr}(\mathrm {S}_{\mathrm {LCH}})_{\mathsf {propfib},\mathsf {all}}^{pt//})$. Hence, the claimed isomorphism follows.
Step 4: identifying ![]() $\,\mathbb {T}_{\mathrm {VTop}}^{\mathrm {Corr}}(p:VG\to G)$ with
$\,\mathbb {T}_{\mathrm {VTop}}^{\mathrm {Corr}}(p:VG\to G)$ with ![]() $\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}(p:VG\to G)$. Following the diagram (A.3.11),
$\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}(p:VG\to G)$. Following the diagram (A.3.11), ![]() $(p:VG\to G)\in \mathrm {CAlg}(\mathrm {Corr}(\mathrm {VTop}))_{\mathsf {propfib}', \mathsf {all}}$ descends to an element in
$(p:VG\to G)\in \mathrm {CAlg}(\mathrm {Corr}(\mathrm {VTop}))_{\mathsf {propfib}', \mathsf {all}}$ descends to an element in ![]() $\mathrm {CAlg}(\mathrm {Corr}(\mathcal {V}\mathcal {S}\mathrm {pc})_{\mathsf {hpf}', \mathsf {hpf}'})$ that comes from ‘the classical’
$\mathrm {CAlg}(\mathrm {Corr}(\mathcal {V}\mathcal {S}\mathrm {pc})_{\mathsf {hpf}', \mathsf {hpf}'})$ that comes from ‘the classical’ ![]() $(p:VG\to G)\in \mathrm {CAlg}(\mathcal {V}\mathcal {S}\mathrm {pc}_{\mathsf {hpf}'})$ under the 1-full symmetric monoidal inclusion
$(p:VG\to G)\in \mathrm {CAlg}(\mathcal {V}\mathcal {S}\mathrm {pc}_{\mathsf {hpf}'})$ under the 1-full symmetric monoidal inclusion ![]() $\mathcal {V}\mathcal {S}\mathrm {pc}_{\mathsf {hpf}'}\to \mathrm {Corr}(\mathcal {V}\mathcal {S}\mathrm {pc})_{\mathsf {hpf}', \mathsf {hpf}'}$. Let
$\mathcal {V}\mathcal {S}\mathrm {pc}_{\mathsf {hpf}'}\to \mathrm {Corr}(\mathcal {V}\mathcal {S}\mathrm {pc})_{\mathsf {hpf}', \mathsf {hpf}'}$. Let ![]() $((\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}//})_{\mathcal {R}}$ be the 1-full subcategory of
$((\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}//})_{\mathcal {R}}$ be the 1-full subcategory of ![]() $(\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}//}$ consisting of left adjointable functors. It follows that
$(\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}//}$ consisting of left adjointable functors. It follows that ![]() $\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}_{\mathsf {hpf}'}}^{\mathrm {Corr}}(p:VG\to G)\in \mathrm {CAlg}((\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}//})$ is the image of
$\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}_{\mathsf {hpf}'}}^{\mathrm {Corr}}(p:VG\to G)\in \mathrm {CAlg}((\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}//})$ is the image of ![]() $\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}(p:VG\to G)\in \mathrm {CcoAlg}(((\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}//})_\mathcal {R})$, through the procedure of passing to the left adjoints of the 1-morphisms.
$\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}(p:VG\to G)\in \mathrm {CcoAlg}(((\mathbf {Pr}_{\mathrm {st}}^{\mathrm {L}})^{\mathrm {Sp}//})_\mathcal {R})$, through the procedure of passing to the left adjoints of the 1-morphisms.
The above fits into the broader setting in Lemma A.23, using the last part of Remark A.9. Since ![]() $\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}(p:VG\to G)\in \mathrm {CcoAlg}((\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {R}})^{\mathrm {Sp}/}))_\mathcal {L}$ (here
$\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}(p:VG\to G)\in \mathrm {CcoAlg}((\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {R}})^{\mathrm {Sp}/}))_\mathcal {L}$ (here ![]() $\mathcal {L}$ means the full subcategory consisting of
$\mathcal {L}$ means the full subcategory consisting of ![]() $\mathrm {Sp}\to C$ whose underlying functor is right adjointable), it certainly lies in
$\mathrm {Sp}\to C$ whose underlying functor is right adjointable), it certainly lies in ![]() $(\mathrm {CcoAlg}(((\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}})^{2\text {-}{\rm op}})^{\mathrm {Sp}//}))_\mathcal {L}$, hence we can equally view the correspondence between
$(\mathrm {CcoAlg}(((\mathbf {Pr}_{\mathrm {st}}^{\mathrm {R}})^{2\text {-}{\rm op}})^{\mathrm {Sp}//}))_\mathcal {L}$, hence we can equally view the correspondence between ![]() $\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}_{\mathsf {hpf}'}}^{\mathrm {Corr}}(p:VG\to G)$ and
$\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}_{\mathsf {hpf}'}}^{\mathrm {Corr}}(p:VG\to G)$ and ![]() $\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}(p:VG\to G)$ through the bottom isomorphism in (A.4.3).
$\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}(p:VG\to G)$ through the bottom isomorphism in (A.4.3).
Step 5: final step. By definition (and tautology), ![]() $J$ is represented by
$J$ is represented by ![]() $\mathbb {T}(p:VG\to G)\cong \mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}(p: VG\to G)$, as a diagram (A.4.2) (which actually factors through
$\mathbb {T}(p:VG\to G)\cong \mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}}(p: VG\to G)$, as a diagram (A.4.2) (which actually factors through ![]() $\Delta ^1\times N(\mathrm {Fin}_*)^{\rm op}$) whose restriction to
$\Delta ^1\times N(\mathrm {Fin}_*)^{\rm op}$) whose restriction to ![]() $\{0\}\times N(\mathrm {Fin}_*)^{\rm op}$ (respectively,
$\{0\}\times N(\mathrm {Fin}_*)^{\rm op}$ (respectively, ![]() $\{1\}\times N(\mathrm {Fin}_*)^{\rm op}$) gives
$\{1\}\times N(\mathrm {Fin}_*)^{\rm op}$) gives ![]() $\mathrm {Sp}$ (respectively,
$\mathrm {Sp}$ (respectively, ![]() $\mathrm {Loc}(G;\mathrm {Sp})$) as a coalgebra in
$\mathrm {Loc}(G;\mathrm {Sp})$) as a coalgebra in ![]() $(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {R}})^{\otimes }$. By transiting the diagram to (A.4.1), we get the corresponding commutative algebra in
$(\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {R}})^{\otimes }$. By transiting the diagram to (A.4.1), we get the corresponding commutative algebra in ![]() $\mathrm {Loc}(G;\mathrm {Sp})\in \mathrm {CAlg}((\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})^{\otimes })$. However, by the previous step, this is exactly
$\mathrm {Loc}(G;\mathrm {Sp})\in \mathrm {CAlg}((\mathcal {P}\mathrm {r}_{\mathrm {st}}^{\mathrm {L}})^{\otimes })$. However, by the previous step, this is exactly ![]() $\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}_{\mathsf {hpf}'}}^{\mathrm {Corr}}(p:VG\to G)\cong \mathbb {T}_{\mathrm {VTop}}^{\mathrm {Corr}}(p:VG\to G)$. Combining with Step 3, the proof is complete.
$\mathbb {T}_{\mathcal {V}\mathcal {S}\mathrm {pc}_{\mathsf {hpf}'}}^{\mathrm {Corr}}(p:VG\to G)\cong \mathbb {T}_{\mathrm {VTop}}^{\mathrm {Corr}}(p:VG\to G)$. Combining with Step 3, the proof is complete.