Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-22T11:52:39.176Z Has data issue: false hasContentIssue false
  • English
  • Français

Groups of piecewise linear homeomorphisms of flows

Part of: Structure and classification of infinite or finite groups Special aspects of infinite or finite groups Topological dynamics

Published online by Cambridge University Press:  05 October 2020

Nicolás Matte Bon  and
Michele Triestino
Nicolás Matte Bon
Affiliation:
CNRS & Institut Camille Jordan (ICJ, UMR CNRS 5208), Université de Lyon, 43 blvd. du 11 novembre 1918, 69622Villeurbanne, [email protected]
Michele Triestino
Affiliation:
Institut de Mathématiques de Bourgogne (IMB, UMR CNRS 5584), Université Bourgogne Franche-Comté, 9 av. Alain Savary, 21000Dijon, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

To every dynamical system 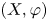$(X,\varphi )$ over a totally disconnected compact space, we associate a left-orderable group 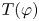$T(\varphi )$. It is defined as a group of homeomorphisms of the suspension of 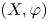$(X,\varphi )$ which preserve every orbit of the suspension flow and act by dyadic piecewise linear homeomorphisms in the flow direction. We show that if the system is minimal, the group is simple and, if it is a subshift, then the group is finitely generated. The proofs of these two statements are short and elementary, providing straightforward examples of finitely generated simple left-orderable groups. We show that if the system is minimal, every action of the corresponding group on the circle has a fixed point. These constitute the first examples of finitely generated left-orderable groups with this fixed point property. We show that for every system 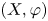$(X,\varphi )$, the group 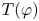$T(\varphi )$ does not have infinite subgroups with Kazhdan's property 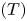$(T)$. In addition, we show that for every minimal subshift, the corresponding group is never finitely presentable. Finally, if 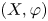$(X,\varphi )$ has a dense orbit, then the isomorphism type of the group 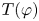$T(\varphi )$ is a complete invariant of flow equivalence of the pair 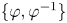$\{\varphi , \varphi ^{-1}\}$.

Keywords

group actions on one-manifoldsorderable groupssimple groupsfinitely generated groupstopological dynamics

MSC classification

Primary: 20F60: Ordered groups 20E32: Simple groups 20F05: Generators, relations, and presentations
Secondary: 37B10: Symbolic dynamics
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 8 , August 2020 , pp. 1595 - 1622
Copyright
Copyright © The Author(s) 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The second author was partially supported by the project ANR Gromeov (ANR-19-CE40-0007) and the project ANER Agroupes (AAP 2019 Région Bourgogne-Franche-Comté).

References

Aliste-Prieto, J. and Petite, S., On the simplicity of homeomorphism groups of a tilable lamination, Monatsh. Math. 181 (2016), 285–300.CrossRefGoogle Scholar
Bekka, B., de la Harpe, P. and Valette, A., Kazhdan's property (T), New Mathematical Monographs, vol. 11 (Cambridge University Press, Cambridge, 2008).CrossRefGoogle Scholar
Ben Ami, E. and Rubin, M., On the reconstruction problem for factorizable homeomorphism groups and foliated manifolds, Topology Appl. 157 (2010), 1664–1679.CrossRefGoogle Scholar
Bergman, G. M., Right orderable groups that are not locally indicable, Pacific J. Math. 147 (1991), 243–248.CrossRefGoogle Scholar
Bieri, R. and Strebel, R., On groups of PL-homeomorphisms of the real line, Mathematical Surveys and Monographs, vol. 215 (American Mathematical Society, Providence, RI, 2016).CrossRefGoogle Scholar
Boyle, M., Flow equivalence of shifts of finite type via positive factorizations, Pacific J. Math. 204 (2002), 273–317.CrossRefGoogle Scholar
Boyle, M., Carlsen, T. M. and Eilers, S., Flow equivalence and isotopy for subshifts, Dyn. Syst. 32 (2017), 305–325.Google Scholar
Boyle, M. and Chuysurichay, S., The mapping class group of a shift of finite type, J. Mod. Dyn. 13 (2018), 115–145.CrossRefGoogle Scholar
Brin, M. G., The chameleon groups of Richard J. Thompson: automorphisms and dynamics, Inst. Hautes Études Sci. Publ. Math. 84 (1996), 5–33.Google Scholar
Brin, M. G. and Squier, C. C., Groups of piecewise linear homeomorphisms of the real line, Invent. Math. 79 (1985), 485–498.Google Scholar
Calegari, D., Dynamical forcing of circular groups, Trans. Amer. Math. Soc. 358 (2006), 3473–3491.Google Scholar
Cannon, J. W., Floyd, W. J. and Parry, W. R., Introductory notes on Richard Thompson's groups, Enseign. Math. (2) 42 (1996), 215–256.Google Scholar
Ceccherini-Silberstein, T. and Coornaert, M., Cellular automata and groups, Springer Monographs in Mathematics (Springer, Berlin, 2010).CrossRefGoogle Scholar
Cornulier, Y., Commensurating actions for groups of piecewise continuous transformations, Preprint (2018), arXiv:1803.08572.Google Scholar
Deroin, B., Almost-periodic actions on the real line, Enseign. Math. 59 (2013), 183–194.CrossRefGoogle Scholar
Deroin, B., Navas, A. and Rivas, C., Groups, orders and dynamics, Preprint (2014), arXiv:1408.5805.Google Scholar
Epstein, D. B. A., The simplicity of certain groups of homeomorphisms, Compos. Math. 22 (1970), 165–173.Google Scholar
Ghys, É., Groups acting on the circle, Enseign. Math. 47 (2001), 329–407.Google Scholar
Grigorchuk, R. I., Degrees of growth of finitely generated groups, and the theory of invariant means, Izv. Akad. Nauk SSSR Ser. Mat. 48 (1984), 939–985 (in Russian).Google Scholar
Grigorchuk, R. I. and Medynets, K. S., On the algebraic properties of topological full groups, Mat. Sb. 205 (2014), 87–108 (in Russian, with Russian summary); Engl. transl., Sb. Math. 205 (2014), 843–861.Google Scholar
Gromov, M., Random walk in random groups, Geom. Funct. Anal. 13 (2003), 73–146.Google Scholar
Higman, G., On infinite simple permutation groups, Publ. Math. Debrecen 3 (1954), 221–226.Google Scholar
Hyde, J. and Lodha, Y., Finitely generated infinite simple groups of homeomorphisms of the real line, Invent. Math. 218 (2019), 83–112.CrossRefGoogle Scholar
Hyde, J., Lodha, Y., Navas, A. and Rivas, C., Uniformly perfect finitely generated simple left orderable groups, Ergodic Theory Dynam. Systems 1–19, doi:10.1017/etds.2019.59.Google Scholar
Juschenko, K. and Monod, N., Cantor systems, piecewise translations and simple amenable groups, Ann. of Math. (2) 178 (2013), 775–787.CrossRefGoogle Scholar
Kim, S.-H., Koberda, T. and Mj, M., Flexibility of group actions on the circle, Lecture Notes in Mathematics, vol. 2231 (Springer, Cham, 2018).Google Scholar
Le Boudec, A. and Matte Bon, N., Subgroup dynamics and $C^{*}$-simplicity of groups of homeomorphisms, Ann. Sci. Éc. Norm. Supér. (4) 51 (2018), 557–602.Google Scholar
Lodha, Y., Matte Bon, N. and Triestino, M., Property FW, differentiable structures, and smoothability of singular actions, J. Topol. 13 (2020), 1119–1138.Google Scholar
Margulis, G., Free subgroups of the homeomorphism group of the circle, C. R. Acad. Sci. Paris Sér. I Math. 331 (2000), 669–674.CrossRefGoogle Scholar
Matui, H., Some remarks on topological full groups of Cantor minimal systems, Internat. J. Math. 17 (2006), 231–251.CrossRefGoogle Scholar
Navas, A., Actions de groupes de Kazhdan sur le cercle, Ann. Sci. Éc. Norm. Supér. (4) 35 (2002), 749–758.CrossRefGoogle Scholar
Navas, A., Groups of circle diffeomorphisms, Chicago Lectures in Mathematics (University of Chicago Press, Chicago, IL, 2011).Google Scholar
Navas, A., Group actions on 1-manifolds: a list of very concrete open questions, in Proc. Int. Congr. Mathematicians, vol. 2, eds B. Sirakov, P. Ney de Souza and M. Viana (World Scientific, Singapore, 2018), 2029–2056.Google Scholar
Nekrashevych, V., Finitely presented groups associated with expanding maps, in Geometric and cohomological group theory, London Mathematical Society Lecture Note Series, vol. 444 (Cambridge University Press, Cambridge, 2018), 115–171.Google Scholar
Parry, B. and Sullivan, D., A topological invariant of flows on $1$-dimensional spaces, Topology 14 (1975), 297–299.Google Scholar
Schmieding, S. and Yang, K., The mapping class group of a minimal subshift, Colloq. Math., published online, 3 July 2020, doi:10.4064/cm7933-2-2020.CrossRefGoogle Scholar
Schreier, J. and Ulam, S., Eine Bemerkung über die Gruppe der topologisehen Abbildungen der Kreislinie auf sich selbst, Studia Math. 5 (1934), 155–159.CrossRefGoogle Scholar
Shalom, Y., Rigidity of commensurators and irreducible lattices, Invent. Math. 141 (2000), 1–54.CrossRefGoogle Scholar
Thurston, W. P., A generalization of the Reeb stability theorem, Topology 13 (1974), 347–352.Google Scholar
Witte Morris, D., Amenable groups that act on the line, Algebr. Geom. Topol. 6 (2006), 2509–2518.Google Scholar