Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Aizenbud, Avraham
Gourevitch, Dmitry
and
Sayag, Eitan
2009.
Generalized Harish-Chandra descent, Gelfand pairs, and an Archimedean analog of Jacquet-Rallis's theorem.
Duke Mathematical Journal,
Vol. 149,
Issue. 3,
Jiang, Dihua
Sun, Binyong
and
Zhu, Chen-Bo
2010.
Uniqueness of Ginzburg-Rallis models: The Archimedean case.
Transactions of the American Mathematical Society,
Vol. 363,
Issue. 5,
p.
2763.
Aizenbud, Avraham
Gourevitch, Dmitry
Rallis, Stephen
and
Schiffmann, Gérard
2010.
Multiplicity one theorems.
Annals of Mathematics,
Vol. 172,
Issue. 2,
p.
1413.
Zhang, Lei
2010.
Gelfand pairs(Sp4n(F),Sp2n(E)).
Journal of Number Theory,
Vol. 130,
Issue. 11,
p.
2428.
Aizenbud, Avraham
Offen, Omer
and
Sayag, Eitan
2011.
Disjoint pairs for GLn(R) and GLn(C).
Comptes Rendus. Mathématique,
Vol. 350,
Issue. 1-2,
p.
9.
Sun, Binyong
and
Zhu, Chen-Bo
2011.
A general form of Gelfand–Kazhdan criterion.
Manuscripta Mathematica,
Vol. 136,
Issue. 1-2,
p.
185.
Sun, Binyong
and
Zhu, Chen-Bo
2012.
Multiplicity one theorems: the Archimedean case.
Annals of Mathematics,
Vol. 175,
Issue. 1,
p.
23.
Gourevitch, Dmitry
Offen, Omer
Sahi, Siddhartha
and
Sayag, Eitan
2012.
Existence of Klyachko models for GL(n,R) and GL(n,C).
Journal of Functional Analysis,
Vol. 262,
Issue. 8,
p.
3585.
Feigon, Brooke
Lapid, Erez
and
Offen, Omer
2012.
On representations distinguished by unitary groups.
Publications mathématiques de l'IHÉS,
Vol. 115,
Issue. 1,
p.
185.
Venketasubramanian, C. G.
2013.
On representations of GL(n) distinguished by GL(n − 1) over a p-adic field.
Israel Journal of Mathematics,
Vol. 194,
Issue. 1,
p.
1.
Aizenbud, Avraham
2013.
A partial analog of the integrability theorem for distributions on p-adic spaces and applications.
Israel Journal of Mathematics,
Vol. 193,
Issue. 1,
p.
233.
GOUREVITCH, DMITRY
SAHI, SIDDHARTHA
and
SAYAG, EITAN
2015.
INVARIANT FUNCTIONALS ON SPEH REPRESENTATIONS.
Transformation Groups,
Vol. 20,
Issue. 4,
p.
1023.
Lapid, Erez
and
Mao, Zhengyu
2015.
Model Transition for Representations of Metaplectic Type.
International Mathematics Research Notices,
Vol. 2015,
Issue. 19,
p.
9486.
Chai, Jingsong
2015.
Some results on archimedean Rankin–Selberg integrals.
Pacific Journal of Mathematics,
Vol. 273,
Issue. 2,
p.
277.
Kemarsky, Alexander
2015.
Gamma factors of distinguished representations of GLn(ℂ).
Pacific Journal of Mathematics,
Vol. 278,
Issue. 1,
p.
137.
Kemarsky, Alexander
2015.
Distinguished representations of GL n (ℂ).
Israel Journal of Mathematics,
Vol. 207,
Issue. 1,
p.
435.
Alesker, Semyon
Gourevitch, Dmitry
and
Sahi, Siddhartha
2016.
On an analytic description of the α-cosine transform on real Grassmannians.
Communications in Contemporary Mathematics,
Vol. 18,
Issue. 02,
p.
1550025.
Alldridge, Alexander
2016.
Fréchet Globalisations of Harish-Chandra Supermodules.
International Mathematics Research Notices,
p.
rnw155.
Sécherre, Vincent
and
Venketasubramanian, Coolimuttam G.
2016.
Modular Representations of ${\rm GL}{(n)}$ Distinguished by ${\rm GL}{(n-1)}$ over a $p$-Adic Field.
International Mathematics Research Notices,
p.
rnw150.
Sayag, Eitan
and
Verma, Mahendra Kumar
2020.
On disjointness of linear models and degenerate Whittaker models.
Journal of Number Theory,
Vol. 207,
Issue. ,
p.
56.
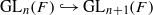 and the two-sided action of GLn(F)×GLn(F) on GLn+1(F). In this paper we show that any GLn(F)×GLn(F)-invariant distribution on GLn+1(F) is invariant with respect to transposition. We show that this implies that the pair (GLn+1(F), GLn(F)) is a Gelfand pair. Namely, for any irreducible admissible representation (π,E) of GLn+1(F),
and the two-sided action of GLn(F)×GLn(F) on GLn+1(F). In this paper we show that any GLn(F)×GLn(F)-invariant distribution on GLn+1(F) is invariant with respect to transposition. We show that this implies that the pair (GLn+1(F), GLn(F)) is a Gelfand pair. Namely, for any irreducible admissible representation (π,E) of GLn+1(F), 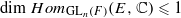 . For the proof in the archimedean case, we develop several tools to study invariant distributions on smooth manifolds.
. For the proof in the archimedean case, we develop several tools to study invariant distributions on smooth manifolds.

