Article contents
Glicci ideals
Published online by Cambridge University Press: 28 June 2013
Abstract
A central problem in liaison theory is to decide whether every arithmetically Cohen–Macaulay subscheme of projective  $n$-space can be linked by a finite number of arithmetically Gorenstein schemes to a complete intersection. We show that this can indeed be achieved if the given scheme is also generically Gorenstein and we allow the links to take place in an
$n$-space can be linked by a finite number of arithmetically Gorenstein schemes to a complete intersection. We show that this can indeed be achieved if the given scheme is also generically Gorenstein and we allow the links to take place in an 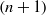 $(n+ 1)$-dimensional projective space. For example, this result applies to all reduced arithmetically Cohen–Macaulay subschemes. We also show that every union of fat points in projective 3-space can be linked in the same space to a union of simple points in finitely many steps, and hence to a complete intersection in projective 4-space.
$(n+ 1)$-dimensional projective space. For example, this result applies to all reduced arithmetically Cohen–Macaulay subschemes. We also show that every union of fat points in projective 3-space can be linked in the same space to a union of simple points in finitely many steps, and hence to a complete intersection in projective 4-space.
Keywords
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2013
References
- 7
- Cited by


