No CrossRef data available.
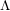 $\unicode[STIX]{x1D6EC}$-adic
$\unicode[STIX]{x1D6EC}$-adic 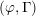 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules and
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules and 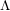 $\unicode[STIX]{x1D6EC}$-adic Hodge theory
$\unicode[STIX]{x1D6EC}$-adic Hodge theoryPublished online by Cambridge University Press: 08 March 2018
We construct the 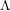 $\unicode[STIX]{x1D6EC}$-adic crystalline and Dieudonné analogues of Hida’s ordinary
$\unicode[STIX]{x1D6EC}$-adic crystalline and Dieudonné analogues of Hida’s ordinary 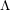 $\unicode[STIX]{x1D6EC}$-adic étale cohomology, and employ integral
$\unicode[STIX]{x1D6EC}$-adic étale cohomology, and employ integral 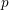 $p$-adic Hodge theory to prove
$p$-adic Hodge theory to prove 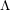 $\unicode[STIX]{x1D6EC}$-adic comparison isomorphisms between these cohomologies and the
$\unicode[STIX]{x1D6EC}$-adic comparison isomorphisms between these cohomologies and the 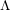 $\unicode[STIX]{x1D6EC}$-adic de Rham cohomology studied in Cais [The geometry of Hida families I:
$\unicode[STIX]{x1D6EC}$-adic de Rham cohomology studied in Cais [The geometry of Hida families I: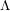 $\unicode[STIX]{x1D6EC}$-adic de Rham cohomology, Math. Ann. (2017), doi:10.1007/s00208-017-1608-1] as well as Hida’s
$\unicode[STIX]{x1D6EC}$-adic de Rham cohomology, Math. Ann. (2017), doi:10.1007/s00208-017-1608-1] as well as Hida’s 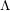 $\unicode[STIX]{x1D6EC}$-adic étale cohomology. As applications of our work, we provide a ‘cohomological’ construction of the family of
$\unicode[STIX]{x1D6EC}$-adic étale cohomology. As applications of our work, we provide a ‘cohomological’ construction of the family of 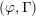 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules attached to Hida’s ordinary
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$-modules attached to Hida’s ordinary 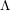 $\unicode[STIX]{x1D6EC}$-adic étale cohomology by Dee [
$\unicode[STIX]{x1D6EC}$-adic étale cohomology by Dee [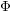 $\unicode[STIX]{x1D6F7}$–
$\unicode[STIX]{x1D6F7}$–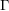 $\unicode[STIX]{x1D6E4}$modules for families of Galois representations, J. Algebra 235 (2001), 636–664], and we give a new and purely geometric proof of Hida’s finiteness and control theorems. We also prove suitable
$\unicode[STIX]{x1D6E4}$modules for families of Galois representations, J. Algebra 235 (2001), 636–664], and we give a new and purely geometric proof of Hida’s finiteness and control theorems. We also prove suitable 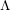 $\unicode[STIX]{x1D6EC}$-adic duality theorems for each of the cohomologies we construct.
$\unicode[STIX]{x1D6EC}$-adic duality theorems for each of the cohomologies we construct.