Published online by Cambridge University Press: 01 March 2008
Let X be a smooth projective curve. We consider the dual reductive pair 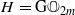 ,
, 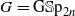 over X, where H splits on an étale two-sheeted covering
over X, where H splits on an étale two-sheeted covering 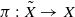 . Let BunG (respectively, BunH) be the stack of G-torsors (respectively, H-torsors) on X. We study the functors FG and FH between the derived categories D(BunG) and D(BunH), which are analogs of the classical theta-lifting operators in the framework of the geometric Langlands program. Assume n=m=1 and H nonsplit, that is,
. Let BunG (respectively, BunH) be the stack of G-torsors (respectively, H-torsors) on X. We study the functors FG and FH between the derived categories D(BunG) and D(BunH), which are analogs of the classical theta-lifting operators in the framework of the geometric Langlands program. Assume n=m=1 and H nonsplit, that is, 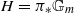 with
with 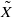 connected. We establish the geometric Langlands functoriality for this pair. Namely, we show that FG :D(BunH)→D(BunG)commutes with Hecke operators with respect to the corresponding map of Langlands L-groups LH→LG. As an application, we calculate Waldspurger periods of cuspidal automorphic sheaves on BunGL2 and Bessel periods of theta-lifts from
connected. We establish the geometric Langlands functoriality for this pair. Namely, we show that FG :D(BunH)→D(BunG)commutes with Hecke operators with respect to the corresponding map of Langlands L-groups LH→LG. As an application, we calculate Waldspurger periods of cuspidal automorphic sheaves on BunGL2 and Bessel periods of theta-lifts from 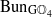 to
to 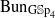 . Based on these calculations, we give three conjectural constructions of certain automorphic sheaves on
. Based on these calculations, we give three conjectural constructions of certain automorphic sheaves on 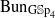 (one of them makes sense for
(one of them makes sense for 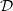 -modules only).
-modules only).