Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-10T20:37:56.036Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometric Langlands in prime characteristic

Part of: Families, fibrations Lie groups

Published online by Cambridge University Press:  16 February 2017

Tsao-Hsien Chen  and
Xinwen Zhu
Tsao-Hsien Chen
Affiliation:
Department of Mathematics, University of Chicago, Chicago, IL 60637, USA email [email protected]
Xinwen Zhu
Affiliation:
Department of Mathematics, California Institute of Technology, 1200 E. California Blvd, Pasadena, CA 91125, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 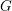$G$ be a semi-simple algebraic group over an algebraically closed field $k$, whose characteristic is positive and does not divide the order of the Weyl group of 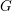$G$, and let 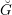$\breve{G}$ be its Langlands dual group over 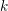$k$. Let 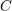$C$ be a smooth projective curve over 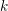$k$ of genus at least two. Denote by 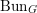$\operatorname{Bun}_{G}$ the moduli stack of 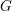$G$-bundles on 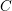$C$ and 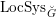$\operatorname{LocSys}_{\breve{G}}$ the moduli stack of 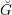$\breve{G}$-local systems on 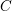$C$. Let 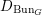$D_{\operatorname{Bun}_{G}}$ be the sheaf of crystalline differential operators on 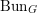$\operatorname{Bun}_{G}$. In this paper we construct an equivalence between the bounded derived category 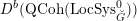$D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0}))$ of quasi-coherent sheaves on some open subset 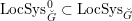$\operatorname{LocSys}_{\breve{G}}^{0}\subset \operatorname{LocSys}_{\breve{G}}$ and bounded derived category $D^{b}(D_{\operatorname{Bun}_{G}}^{0}\text{-}\text{mod})$ of modules over some localization 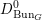$D_{\operatorname{Bun}_{G}}^{0}$ of 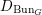$D_{\operatorname{Bun}_{G}}$. This generalizes the work of Bezrukavnikov and Braverman in the 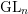$\operatorname{GL}_{n}$ case.

Keywords

Langlands dualityHitchin fibrationD-modules in characteristic p

MSC classification

Primary: 14D24: Geometric Langlands program 22E57: Geometric Langlands program
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 2 , February 2017 , pp. 395 - 452
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arinkin, D., Appendix to [ DP08 ].Google Scholar
Arinkin, D. and Gaitsgory, D., Singular support of coherent sheaves, and the geometric Langlands conjecture, Preprint (2012), arXiv:1201.6343.Google Scholar
Beilinson, A. and Drinfeld, V., Quantization of Hitchin’s integrable system and Hecke eigensheaves, Preprint (1991), http://www.math.uchicago.edu/earinkin/langlands/.Google Scholar
Bezrukavnikov, R. and Braverman, A., Geometric Langlands correspondence for D-modules in prime characteristic: the GL(n) case , Pure Appl. Math. Q. 3 (2007), 153–179.CrossRefGoogle Scholar
Bezrukavnikov, R., Mirković, I. and Rumynin, D., Localization of modules for a semisimple Lie algebra in prime characteristic , Ann. of Math. (2) 167 (2008), 945–991.CrossRefGoogle Scholar
Bezrukavnikov, R. and Travkin, R., Quantization of Hitchin integrable system via positive characteristic, Preprint (2016), arXiv:1603.01327.Google Scholar
Breen, L., Un théoreme d’annulation pour certains Ext de faisceaux abéliens , Ann. Sci. Éc. Norm. Supér. (4) 5 (1975), 339–352.CrossRefGoogle Scholar
Bosch, S., Lutkebohmert, W. and Raynaud, M., Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), vol. 21 (Springer, Berlin, 1990).CrossRefGoogle Scholar
Brochard, S., Foncteur de Picard d’un champ algébrique , Math. Ann. 343 (2009), 541–602.CrossRefGoogle Scholar
Chen, T.-H. and Zhu, X., Non-abelian Hodge theory for curves in characteristic p , Geom. Funct. Anal. 25 (2015), 1706–1733.CrossRefGoogle Scholar
Deligne, P., La formule de dualité globale , in SGA 4, tome 3, Expose XVIII, Lecture Notes in Mathematics, vol. 305 (Springer, Berlin, 1973), 481–587.Google Scholar
Donagi, R. and Gaitsgory, D., The gerbe of Higgs bundles , Transform. Groups 7 (2002), 109–153.CrossRefGoogle Scholar
Donagi, R. and Pantev, T., Torus fibrations, gerbes, and duality (with an appendix by Dmitry Arinkin) , Mem. Amer. Math. Soc. 193 (2008), no. 901.Google Scholar
Donagi, R. and Pantev, T., Langlands duality for Hitchin systems , Invent. Math. 189 (2012), 653–735.CrossRefGoogle Scholar
Frenkel, E., Gaitsgory, D. and Vilonen, K., Whittaker patterns in the geometry of moduli spaces of bundles on curves , Ann. of Math. (2) 153 (2001), 699–748.CrossRefGoogle Scholar
Frenkel, E. and Witten, E., Geometric endoscopy and mirror symmetry , Commun. Number Theory Phys. 2 (2008), 113–283.CrossRefGoogle Scholar
Gaitsgory, D., Outline of the proof of the geometric Langlands conjecture for $\operatorname{GL}_{2}$ , Preprint (2013), arXiv:1302.2506.Google Scholar
Groechenig, M., Moduli of flat connections in positive characteristic, Preprint (2013), arXiv:1201.0741.Google Scholar
Hausel, T. and Thaddeus, M., Mirror symmetry, Langlands duality, and the Hitchin system , Invent. Math. 153 (2003), 197–229.CrossRefGoogle Scholar
Hitchin, N., Stable bundles and integrable systems , Duke Math. J. 54 (1987), 91–114.CrossRefGoogle Scholar
Laumon, G., Transformation de Fourier generalisee, Preprint (1996), arXiv:alg-geom/9603004.Google Scholar
Laumon, G. and Moret-Bailly, L., Champs algébriques, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) (A Series of Modern Surveys in Mathematics), vol. 39 (Springer, Berlin, 2000).CrossRefGoogle Scholar
Mukai, S., Duality between D (X) and D (X̂) with its application to Picard sheaves , Nagoya Math. J. (1981), 153–175.CrossRefGoogle Scholar
Mukai, S., Fourier functor and its application to the moduli of bundles on an abelian variety , in Algebraic geometry, Sendai, 1985, Advanced Studies in Pure Mathematics, vol. 10 (North-Holland, Amsterdam, 1987), 515–550.CrossRefGoogle Scholar
Ngô, B. C., Hitchin fibration and endoscopy , Invent. Math. 164 (2006), 399–453.CrossRefGoogle Scholar
Ngô, B. C., Le lemme fondamental pour les algèbres de Lie , Publ. Math. Inst. Hautes Études Sci. 111 (2010), 1–169.CrossRefGoogle Scholar
Ogus, A. and Vologodsky, V., Nonabelian Hodge theory in characteristic p , Publ. Math. Inst. Hautes Études Sci. 106 (2007), 1–138.CrossRefGoogle Scholar
Osipov, D. and Zhu, X., A categorical proof of the Parshin reciprocity laws on algebraic surfaces , Algebra Number Theory 5 (2011), 289–337.CrossRefGoogle Scholar
Toen, B., Derived Azumaya algebras and generators for twisted derived categories , Invent. Math. 189 (2012), 581–652.CrossRefGoogle Scholar
Travkin, R., Quantum geometric Langlands in positive characteristic, Preprint (2011), arXiv:1110.5707.Google Scholar
Yun, Z., Global Springer theory , Adv. Math. 228 (2011), 266–328.CrossRefGoogle Scholar