Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-22T16:51:11.848Z Has data issue: false hasContentIssue false
  • English
  • Français

Genus 0 characteristic numbers of the tropical projective plane

Part of: Projective and enumerative geometry

Published online by Cambridge University Press:  18 November 2013

Benoît Bertrand ,
Erwan Brugallé  and
Grigory Mikhalkin
Benoît Bertrand
Affiliation:
Institut Mathématiques de Toulouse, Université Paul Sabatier, 118 route de Narbonne, F-31062 Toulouse Cedex 9, France email [email protected]
Erwan Brugallé
Affiliation:
Université Pierre et Marie Curie, Paris 6, 4 place Jussieu, 75 005 Paris, France email [email protected]
Grigory Mikhalkin
Affiliation:
Section de mathématiques Université de Genève, Villa Battelle, 7 route de Drize, 1227 Carouge, Suisse, Switzerland email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Finding the so-called characteristic numbers of the complex projective plane 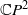$ \mathbb{C} {P}^{2} $ is a classical problem of enumerative geometry posed by Zeuthen more than a century ago. For a given 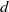$d$ and 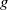$g$ one has to find the number of degree 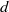$d$ genus 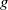$g$ curves that pass through a certain generic configuration of points and at the same time are tangent to a certain generic configuration of lines. The total number of points and lines in these two configurations is 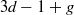$3d- 1+ g$ so that the answer is a finite integer number. In this paper we translate this classical problem to the corresponding enumerative problem of tropical geometry in the case when 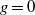$g= 0$. Namely, we show that the tropical problem is well posed and establish a special case of the correspondence theorem that ensures that the corresponding tropical and classical numbers coincide. Then we use the floor diagram calculus to reduce the problem to pure combinatorics. As a consequence, we express genus 0 characteristic numbers of 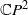$ \mathbb{C} {P}^{2} $ in terms of open Hurwitz numbers.

Keywords

tropical geometrycharacteristic numbersenumerative geometryprojective plane

MSC classification

Secondary: 14T05: Tropical geometry 14N10: Enumerative problems (combinatorial problems)
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 1 , January 2014 , pp. 46 - 104
Copyright
© The Author(s) 2013 

References

Ardila, F. and Block, F., Universal polynomials for Severi degrees of toric surfaces, Adv. Math. 237 (2013), 165–193.CrossRefGoogle Scholar
Arroyo, A., Brugallé, E. and Lopez de Medrano, L., Recursive formula for Welschinger invariants, Int. Math. Res. Not. IMRN 5 (2011), 1107–1134.Google Scholar
Aluffi, P., The characteristic numbers of smooth plane cubics, in Algebraic geometry, Sundance, UT, 1986, Lecture Notes in Mathematics, vol. 1311 (Springer, Berlin, 1988), 1–8.Google Scholar
Aluffi, P., The enumerative geometry of plane cubics. I. Smooth cubics, Trans. Amer. Math. Soc. 317 (1990), 501–539.Google Scholar
Aluffi, P., The enumerative geometry of plane cubics. II. Nodal and cuspidal cubics, Math. Ann. 289 (1991), 543–572.CrossRefGoogle Scholar
Aluffi, P., Two characteristic numbers for smooth plane curves of any degree, Trans. Amer. Math. Soc. 329 (1992), 73–96.Google Scholar
Bertrand, B., Real Zeuthen numbers for two lines, Int. Math. Res. Not. IMRN (2008), Article ID rnn014.CrossRefGoogle Scholar
Bertrand, B., Énumeration asymtotique de courbes réelles de cogenre fixé, in preparation.Google Scholar
Bertrand, B., Brugallé, E. and Mikhalkin, G., Tropical open Hurwitz numbers, Rend. Semin. Mat. Univ. Padova 125 (2011), 157–171.CrossRefGoogle Scholar
Block, F., Gathmann, A. and Markwig, H., Psi-floor diagrams and a Caporaso–Harris type recursion, Israel J. Math. 191 (2012), 405–449.CrossRefGoogle Scholar
Brugallé, E. and Lopez de Medrano, L., Inflection points of real and tropical plane curves, J. Singul. 4 (2012), 74–103.Google Scholar
Brugallé, E. and Mikhalkin, G., Enumeration of curves via floor diagrams, C. R. Math. Acad. Sci. Paris 345 (2007), 329–334.Google Scholar
Brugallé, E. and Mikhalkin, G., Floor decompositions of tropical curves: the planar case, in Proc. fifteenth Gökova geometry-topology conference, 2008 (International Press, Boston, MA, 2009), 64–90.Google Scholar
Brugallé, E. and Mikhalkin, G., Floor decompositions of tropical curves in any dimension, in preparation, preliminary version available at http://www.math.jussieu.fr/~brugalle/miscellaneous.html.Google Scholar
Brugallé, E. and Mikhalkin, G., Realizability of superabundant curves, in preparation.Google Scholar
Brugallé, E. and Puignau, N., Enumeration of real conics and maximal configurations, J. Eur. Math. Soc. (JEMS), to appear.Google Scholar
Berline, N., Plagne, A. and Sabbah (eds), C., Géométrie tropicale, Éditions de l’école Polytechnique, Palaiseau (2008), http://www.math.polytechnique.fr/xups/vol08.html.Google Scholar
Caporaso, L. and Harris, J., Counting plane curves of any genus, Invent. Math. 131 (1998), 345–392.Google Scholar
Cavalieri, R., Johnson, P. and Markwig, H., Tropical Hurwitz numbers, J. Algebraic Combin. 32 (2010), 241–265.Google Scholar
Chasles, M., Construction des coniques qui satisfont à cinq conditions, C. R. Acad. Sci. Paris 58 (1864), 297–308.Google Scholar
Dickenstein, A. and Tabera, L. F., Singular tropical hypersurfaces, Discrete Comput. Geom. 47 (2012), 430–453.Google Scholar
Eliashberg, Y., Givental, A. and Hofer, H., Introduction to symplectic field theory, Visions in mathematics: Towards 2000, GAFA, Geom. Funct. Anal. Special Volume – GAFA2000, Part II, 560–673.CrossRefGoogle Scholar
Fomin, S. and Mikhalkin, G., Labelled floor diagrams for plane curves, J. Eur. Math. Soc. (JEMS) 12 (2010), 1453–1496.Google Scholar
Gathmann, A. and Markwig, H., The numbers of tropical plane curves through points in general position, J. Reine Angew. Math. 602 (2007), 155–177.Google Scholar
Gathmann, A. and Markwig, H., Kontsevich’s formula and the WDVV equations in tropical geometry, Adv. Math. 217 (2008), 537–560.Google Scholar
Gelfand, I. M., Kapranov, M. M. and Zelevinsky, A. V., Discriminants, resultants, and multidimensional determinants, in Mathematics: theory & applications (Birkhäuser, Boston, MA, 1994).Google Scholar
Ghys, E., Trois mille deux cent soixante-quatre …, Images des Mathématiques, Centre national de la recherche scientifique (2008), http://images.math.cnrs.fr/Trois-mille-deux-cent-soixante.html.Google Scholar
Graber, T., Kock, J. and Pandharipande, R., Descendant invariants and characteristic numbers, Amer. J. Math. 124 (2002), 611–647.Google Scholar
Ionel, E.-N. and Parker, T. H., The symplectic sum formula for Gromov–Witten invariants, Ann. of Math. (2) 159 (2004), 935–1025.CrossRefGoogle Scholar
Itenberg, I., Kharlamov, V. and Shustin, E., Welschinger invariant and enumeration of real rational curves, Int. Math. Res. Not. IMRN 49 (2003), 2639–2653.CrossRefGoogle Scholar
Itenberg, I., Mikhalkin, G and Shustin, E., Tropical algebraic geometry, Oberwolfach Seminars Series, vol. 35 (Birkhäuser, 2007).Google Scholar
Maillard, S., Recherche des caractéristiques des systèmes élémentaires de courbes planes du troisième ordre, PhD thesis, Faculté des sciences de Paris, 1871.Google Scholar
Mikhalkin, G., Real algebraic curves, the moment map and amoebas, Ann. of Math. (2) 151 (2000), 309–326.CrossRefGoogle Scholar
Mikhalkin, G., Decomposition into pairs-of-pants for complex algebraic hypersurfaces, Topology 43 (2004), 1035–1065.Google Scholar
Mikhalkin, G., Enumerative tropical algebraic geometry in ${ \mathbb{R} }^{2} $, J. Amer. Math. Soc. 18 (2005), 313–377.CrossRefGoogle Scholar
Mikhalkin, G., Tropical geometry and its applications, Proc. International Congress of Mathematicians, Madrid, 2006, Vol. II (European Mathematical Society, Zürich, 2006), 827–852.Google Scholar
Mikhalkin, G., What is…a tropical curve? Notices Amer. Math. Soc. 54 (2007), 511–513.Google Scholar
Mikhalkin, G., Phase-tropical curves I. Realizability and enumeration, in preparation.Google Scholar
Mikhalkin, G. and Okounkov, A., Geometry of planar log-fronts, Mosc. Math. J. 7 (2007), 507–531, 575.Google Scholar
Nishinou, T., Correspondence theorems for tropical curves, Preprint (2010), math.AG/0912.5090.Google Scholar
Nishinou, T. and Siebert, B., Toric degenerations of toric varieties and tropical curves, Duke Math. J. 135 (2006), 1–51.Google Scholar
Pandharipande, R., Intersections of $\mathbf{Q} $-divisors on Kontsevich’s moduli space ${ \overline{M} }_{0, n} ({\mathbf{P} }^{r} , d)$ and enumerative geometry, Trans. Amer. Math. Soc. 351 (1999), 1481–1505.Google Scholar
Passare, M., How to compute $\sum 1/ {n}^{2} $ by solving triangles, Amer. Math. Monthly 115 (2008), 745–752.CrossRefGoogle Scholar
Richter-Gebert, J., Sturmfels, B. and Theobald, T., First steps in tropical geometry, in Idempotent mathematics and mathematical physics, Contemporary Mathematics, vol. 377 (American Mathematical Society, Providence, RI, 2005), 289–317.Google Scholar
Ronga, F., Tognoli, A. and Vust, T., The number of conics tangent to five given conics: the real case, Rev. Mat. Univ. Complutense Madr. 10 (1997), 391–421.Google Scholar
Schubert, H., Kalkül der abzählenden Geometrie (Springer, Berlin, 1979), reprint of the 1879 original, with an introduction by Steven L. Kleiman.Google Scholar
Shustin, E., Patchworking singular algebraic curves, non-Archimedean amoebas and enumerative geometry, Algebra i Analiz 17 (2005), 170–214.Google Scholar
Sottile, F., 3264 real conics, Preprint, http://www.math.tamu.edu/~sottile/research/stories/3264/index.html.Google Scholar
Thurston, W., Three-dimensional geometry and topology. Vol. 1, Princeton Mathematical Series, vol. 35, ed. Levy, Silvio (Princeton University Press, Princeton, NJ, 1997).Google Scholar
Tyomkin, I., Tropical geometry and correspondence theorems via toric stacks, Math. Ann. 353 (2012), 945–995.CrossRefGoogle Scholar
Vakil, R., The characteristic numbers of quartic plane curves, Canad. J. Math. 51 (1999), 1089–1120.Google Scholar
Vakil, R., The enumerative geometry of rational and elliptic curves in projective space, J. Reine Angew. Math. 529 (2000), 101–153.Google Scholar
Vakil, R., Recursions for characteristic numbers of genus one plane curves, Ark. Mat. 39 (2001), 157–180.Google Scholar
Viro, O. Ya., Some integral calculus based on Euler characteristic, Lecture Notes in Mathematics, vol. 1346 (Springer, 1988), 127–138.Google Scholar
Viro, O., Dequantization of real algebraic geometry on logarithmic paper, in European Congress of Mathematics, Barcelona, 2000, Vol. I, Progress in Mathematics, vol. 201 (Birkhäuser, Basel, 2001), 135–146.Google Scholar
Welschinger, J. Y., Towards relative invariants of real symplectic 4-manifolds, Geom. Funct. Anal. 16 (2006), 1157–1182.Google Scholar
Zeuthen, H. G., Déterminations des caractéristique des systémes élémentaires de cubiques, C. R. Math. Acad. Sci. Paris 74 (1872), 521–526.Google Scholar
Zeuthen, H. G., Almindelige Egenskaber ved Systemer af plane Kurver, Naturvidenskabelig og Mathematisk Afdeling 10 (1873), 286–393.Google Scholar