Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T10:58:11.154Z Has data issue: false hasContentIssue false
  • English
  • Français

Generic rank of Betti map and unlikely intersections

Part of: Arithmetic algebraic geometry Arithmetic problems. Diophantine geometry Abelian varieties and schemes

Published online by Cambridge University Press:  12 January 2021

Ziyang Gao
Ziyang Gao*
Affiliation:
CNRS, IMJ-PRG, 4 place Jussieu, 75005Paris, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 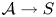$\mathcal {A} \rightarrow S$ be an abelian scheme over an irreducible variety over 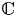$\mathbb {C}$ of relative dimension 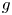$g$. For any simply-connected subset $\Delta$ of 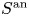$S^{\mathrm {an}}$ one can define the Betti map from 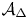$\mathcal {A}_{\Delta }$ to 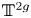$\mathbb {T}^{2g}$, the real torus of dimension 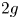$2g$, by identifying each closed fiber of 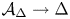$\mathcal {A}_{\Delta } \rightarrow \Delta$ with 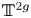$\mathbb {T}^{2g}$ via the Betti homology. Computing the generic rank of the Betti map restricted to a subvariety 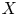$X$ of 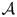$\mathcal {A}$ is useful to study Diophantine problems, e.g. proving the geometric Bogomolov conjecture over char 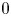$0$ and studying the relative Manin–Mumford conjecture. In this paper we give a geometric criterion to detect this rank. As an application we show that it is maximal after taking a large fibered power (if 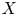$X$ satisfies some conditions); it is an important step to prove the bound for the number of rational points on curves (Dimitrov et al., Uniformity in Mordell–Lang for Curves, Preprint (2020), arXiv:2001.10276). Another application is to answer a question of André, Corvaja and Zannier and improve a result of Voisin. We also systematically study its link with the relative Manin–Mumford conjecture, reducing the latter to a simpler conjecture. Our tools are functional transcendence and unlikely intersections for mixed Shimura varieties.

Keywords

Abelian schemeBetti mapBetti rankunlikely intersections

MSC classification

Primary: 11G10: Abelian varieties of dimension $> 1$ 11G50: Heights 14G25: Global ground fields 14K15: Arithmetic ground fields
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 12 , December 2020 , pp. 2469 - 2509
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

André, Y., Corvaja, P. and Zannier, U., The Betti map associated to a section of an abelian scheme (with an appendix by Z. Gao), Invent. Math. 222 (2020), 161–202.CrossRefGoogle Scholar
André, Y., Mumford–Tate groups of mixed Hodge structures and the theorem of the fixed part, Compos. Math. 82 (1992), 1–24.Google Scholar
Bertrand, D., Masser, D., Pillay, A. and Zannier, U., Relative Manin–Mumford for semi-abelain surfaces, Proc. Edinb. Math. Soc. 59 (2016), 837–875.CrossRefGoogle Scholar
Cantat, S., Gao, Z., Habegger, P. and Xie, J., The geometric Bogomolov conjecture, Duke Math. J. (2020), https://doi.org/10.1215/00127094-2020-0044.CrossRefGoogle Scholar
Corvaja, P., Masser, D. and Zannier, U., Torsion hypersurfaces on abelian schemes and Betti coordinates, Math. Ann. 371 (2018), 1013–1045.CrossRefGoogle Scholar
Daw, C. and Ren, J., Applications of the hyperbolic Ax-Schanuel conjecture, Compos. Math. 154 (2018), 1843–1888.CrossRefGoogle Scholar
Deligne, P., Théorie de Hodge: II, Publ. Math. Inst. Hautes Études Sci. 40 (1971), 5–57.CrossRefGoogle Scholar
Dimitrov, V., Gao, Z. and Habegger, P., Uniformity in Mordell–Lang for curves, Preprint (2020), arXiv:2001.10276.Google Scholar
Gao, Z., A special point problem of André-Pink-Zannier in the universal family of abelian varieties, Ann. Sc. Norm. Super. Pisa Cl. Sci. 17 (2017), 231–266.Google Scholar
Gao, Z., Towards the André-Oort conjecture for mixed Shimura varieties: the Ax-Lindemann-Weierstrass theorem and lower bounds for Galois orbits of special points, J. Reine Angew. Math. 732 (2017), 85–146.CrossRefGoogle Scholar
Gao, Z., Mixed Ax–Schanuel for the universal abelian varieties and some applications, Compos. Math. 156 (2020), 2263–2297.CrossRefGoogle Scholar
Gao, Z. and Habegger, P., Heights in families of abelian varieties and the geometric Bogomolov conjecture, Ann. of Math. (2) 189 (2019), 527–604.CrossRefGoogle Scholar
Genestier, A. and Ngô, B. C., Lecture on Shimura varieties, in Autour de motifs, Ecole d'été Franco-Asiatique de Géométrie Algébrique et de Théorie des Nombres/Asian-French Summer School on Algebraic Geometry and Number Theory, Vol. I, Panoramas et Synthéses, vol. 29, (Société Mathématique de France, 2009), 187–236.Google Scholar
Habegger, P. and Pila, J., O-minimality and certain atypical intersections, Ann. Sci. Éc. Norm. Supér. (4) 49 (2016), 813–858.CrossRefGoogle Scholar
Klingler, B., Ullmo, E. and Yafaev, A., The hyperbolic Ax-Lindemann-Weierstrass conjecture, Publ. Math. Inst. Hautes Études Sci. 123 (2016), 333–360.CrossRefGoogle Scholar
Masser, D. and Zannier, U., Torsion points on families of squares of elliptic curves, Math. Ann. 352 (2012), 453–484.CrossRefGoogle Scholar
Masser, D. and Zannier, U., Torsion points on families of products of elliptic curves, Adv. Math. 259 (2014), 116–133.CrossRefGoogle Scholar
Masser, D. and Zannier, U., Torsion points on families of simple abelian surfaces and Pell's equation over polynomial rings (with an appendix by E. V. Flynn), J. Eur. Math. Soc. 17 (2015), 2379–2416.CrossRefGoogle Scholar
Masser, D. and Zannier, U., Torsion points, Pell's equation, and integration in elementary terms, Preprint (2018), submitted.Google Scholar
Mok, N., Pila, J. and Tsimerman, J., Ax-Schanuel for Shimura varieties, Ann. of Math. (2) 189 (2019), 945–978.CrossRefGoogle Scholar
Peters, C. and Steenbrink, J., Mixed Hodge structures, A Series of Modern Surveys in Mathematics, vol. 52 (Springer, 2008).Google Scholar
Pink, R., Arithmetical compactification of mixed Shimura varieties, PhD thesis, Bonner Mathematische Schriften (1989).Google Scholar
Raynaud, M., Courbes sur une variété abélienne et points de torsion, Inv. Math. 71 (1983), 207–233.CrossRefGoogle Scholar
Ullmo, E. and Yafaev, A., A characterisation of special subvarieties, Mathematika 57 (2011), 263–273.CrossRefGoogle Scholar
Voisin, C., Torsion points of sections of Lagrangian torus fibrations and the Chow ring of hyper-Kähler manifolds, in Geometry of moduli, eds. J.-A. Christophersen and K. Ranestad (Springer, Cham, 2018), 295–326.CrossRefGoogle Scholar
Zannier, U., Some problems of unlikely intersections in arithmetic and geometry (with appendixes by D. Masser), Annals of Mathematics Studies, vol. 181 (Princeton University Press, 2012).Google Scholar
Zannier, U., Unlikely intersections and Pell's equations in polynomials, in Trends in contemporary mathematics, eds. V. Ancona and E. Strickland (Springer, 2014), 151–169.CrossRefGoogle Scholar