Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-16T18:25:34.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Generic pseudogroups on 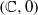$( \mathbb{C} , 0)$ and the topology of leaves

Part of: Complex dynamical systems Differential equations in the complex domain Smooth dynamical systems: general theory

Published online by Cambridge University Press:  01 July 2013

J.-F. Mattei ,
J. C. Rebelo  and
H. Reis
J.-F. Mattei
Affiliation:
Institut de Mathématiques de Toulouse, Université Toulouse 3, 118 Route de Narbonne, F-31062 Toulouse, France email [email protected]
J. C. Rebelo
Affiliation:
Institut de Mathématiques de Toulouse, Université Toulouse 3, 118 Route de Narbonne, F-31062 Toulouse, France email [email protected]
H. Reis
Affiliation:
Centro de Matemática da Universidade do Porto, Faculdade de Economia da Universidade do Porto, Portugal email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that generically a pseudogroup generated by holomorphic diffeomorphisms defined about 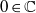$0\in \mathbb{C} $ is free in the sense of pseudogroups even if the class of conjugacy of the generators is fixed. This result has a number of consequences on the topology of leaves for a (singular) holomorphic foliation defined on a neighborhood of an invariant curve. In particular, in the classical and simplest case arising from local nilpotent foliations possessing a unique separatrix which is given by a cusp of the form 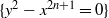$\{ {y}^{2} - {x}^{2n+ 1} = 0\} $, our results allow us to settle the problem of showing that a generic foliation possesses only countably many non-simply connected leaves.

Keywords

pseudogroups on (ℂ,0)free groups in Diff(ℂ,0)nilpotent singularities

MSC classification

Secondary: 34M35: Singularities, monodromy, local behavior of solutions, normal forms 37C85: Dynamics of group actions other than ${bf Z}$ and ${bf R}$, and foliations 37F75: Holomorphic foliations and vector fields
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 8 , August 2013 , pp. 1401 - 1430
Copyright
© The Author(s) 2013 

References

Berthier, M., Cerveau, D. and Lins Neto, A., Sur les feuilletages analytiques réels et le problème du centre, J. Differential Equations 131 (1996), 244–266.Google Scholar
Carleson, L. and Gamelin, T., Complex dynamics (Springer, New York, 1993).Google Scholar
Cerveau, D. and Loray, F., Un théorème de Frobenius singulier via l’arithmétique élémentaire, J. Number Theory 68 (1998), 217–228.CrossRefGoogle Scholar
Ecalle, J. and Vallet, B., Intertwined mappings, Ann. Fac. Sci. Toulouse Math. 13 (2004), 291–376.Google Scholar
Firsova, T., Topology of analytic foliations in ${ \mathbb{C} }^{2} $. The Kupka–Smale property, Tr. Mat. Inst. Steklova 254 (2006), 162–180; translation in Proc. Steklov Inst. Math. 254 (2006), 152–168.Google Scholar
Il’yashenko, Yu. and Pyartli, A. S., The monodromy group at infinity of a generic polynomial vector field on the complex projective plane, Russ. J. Math. Phys. 2 (1994), 275–315.Google Scholar
Le Floch, L., Rigidité générique des feuilletages, Ann. Sci. Éc. Norm Supér. (4) 31 (1998), 765–785.CrossRefGoogle Scholar
Loray, F., A preparation theorem for codimension-one foliations, Ann. of Math. (2) 163 (2006), 709–722.Google Scholar
Marin, D. and Mattei, J.-F., Incompressibilité des feuilles de germes de feuilletages holomorphes singuliers, Ann. Sci. Éc. Norm. Supér. (4) 41 (2008), 855–903.Google Scholar
Martinet, J. and Ramis, J.-P., Classification analytique des équations différentielles non linéaires résonnantes du premier ordre, Ann. Sci. Éc. Norm. Supér. 16 (1983).Google Scholar
Mattei, J.-F. and Moussu, R., Holonomie et intégrales premières, Ann. Sci. Éc. Norm. Supér. 13 (1980), 469–523.Google Scholar
Mattei, J.-F. and Salem, E., Modules formels locaux de feuilletages holomorphes, Preprint (2004), arXiv:math/0402256v1.Google Scholar
Nakai, I. and Yanai, K., Relations of formal diffeomorphisms and the center problem, Mosc. Math. J. 10 (2010), 415–468.CrossRefGoogle Scholar
Strózyna, E. and Zoladek, H., The analytic and formal normal form for the nilpotent singularity, J. Differential Equations 179 (2002), 479–537.Google Scholar
Takens, F., A nonstabilizable jet of a singularity of a vector field: the analytic case, in Algebraic and differential topology—global differential geometry, Teubner-Texte zur Mathematik, vol. 70 (Teubner, Leipzig, 1984), 288–305.Google Scholar
Yoccoz, J.-C., Centralisateurs et conjugaison différentiable des difféomorphismes du cercle. Petits diviseurs en dimension 1, Astérisque 231 (1995), 89–242.Google Scholar