Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-05T03:00:58.022Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized ‘second Ritt theorem’ and explicit solution of the polynomial moment problem

Part of: Qualitative theory Miscellaneous topics of analysis in the complex domain Curves

Published online by Cambridge University Press:  29 January 2013

F. Pakovich
F. Pakovich*
Affiliation:
Department of Mathematics, Ben-Gurion University of the Negev, P.O.B. 653, Beer-Sheva, Israel (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the recent paper by Pakovich and Muzychuk [Solution of the polynomial moment problem, Proc. Lond. Math. Soc. (3) 99 (2009), 633–657] it was shown that any solution of ‘the polynomial moment problem’, which asks to describe polynomials 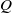$Q$ orthogonal to all powers of a given polynomial 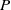$P$ on a segment, may be obtained as a sum of so-called ‘reducible’ solutions related to different decompositions of 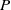$P$ into a composition of two polynomials of lower degrees. However, the methods of that paper do not permit us to estimate the number of necessary reducible solutions or to describe them explicitly. In this paper we provide a description of polynomial solutions of the functional equation 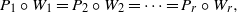$P_1\circ W_1=P_2\circ W_2=\cdots =P_r\circ W_r,$and on this base describe solutions of the polynomial moment problem in an explicit form suitable for applications.

Keywords

polynomial moment problemsecond Ritt theorempolynomial decompositionscenter problem

MSC classification

Secondary: 30E99: None of the above, but in this section 14H30: Coverings, fundamental group 34C99: None of the above, but in this section
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 4 , April 2013 , pp. 705 - 728
Copyright
Copyright © 2013 The Author(s)

References

[BT00]Bilu, Y. and Tichy, R., The Diophantine equation $f(x) = g(y)$, Acta Arith. 95 (2000), 261–288.CrossRefGoogle Scholar
[BBY05]Blinov, M., Briskin, M. and Yomdin, Y., Local center conditions for the Abel equation and cyclicity of its zero solution, in Complex analysis and dynamical systems II: a conference in honor of Professor Lawrence Zalcman’s sixtieth birthday, June 9–12, 2003, Nahariya, Israel, Contemporary Mathematics, vol. 382 (American Mathematical Society, Providence, RI, 2005), 65–82.Google Scholar
[BFY98]Briskin, M., Françoise, J.-P. and Yomdin, Y., Une approche au problème du centre-foyer de Poincaré, C. R. Acad. Sci. Paris, Sér. I, Math. 326 (1998), 1295–1298.Google Scholar
[BFY99]Briskin, M., Françoise, J.-P. and Yomdin, Y., Center conditions, compositions of polynomials and moments on algebraic curve, Ergodic Theory Dynam. Systems 19 (1999), 1201–1220.Google Scholar
[BFY00a]Briskin, M., Françoise, J.-P. and Yomdin, Y., Center condition II: parametric and model center problems, Israel J. Math. 118 (2000), 61–82.Google Scholar
[BFY00b]Briskin, M., Françoise, J.-P. and Yomdin, Y., Center condition III: Parametric and model center problems, Israel J. Math. 118 (2000), 83–108.Google Scholar
[BFY01]Briskin, M., Françoise, J.-P. and Yomdin, Y., Generalized moments, center-focus conditions and compositions of polynomials, in Operator theory, system theory and related topics, Operator Theory: Advances and Applications, vol. 123 (Birkhäuser, Basel, 2001), 161–185.Google Scholar
[BRY10]Briskin, M., Roytvarf, N. and Yomdin, Y., Center conditions at infinity for Abel differential equations, Ann. of Math. (2) 172 (2010), 437–483.CrossRefGoogle Scholar
[BY05]Briskin, M. and Yomdin, Y., Tangential version of Hilbert 16th problem for the Abel equation, Mosc. Math. J. 5 (2005), 23–53.Google Scholar
[Chr00]Christopher, C., Abel equations: composition conjectures and the model problem, Bull. Lond. Math. Soc. 32 (2000), 332–338.Google Scholar
[Eng41]Engstrom, H., Polynomial substitutions, Amer. J. Math. 63 (1941), 249–255.Google Scholar
[Fri73]Fried, M., On a theorem of Ritt and related diophantine problems, J. Reine Angew. Math. 264 (1973), 40–55.Google Scholar
[MP11]Muzychuk, M. and Pakovich, F., Jordan–Holder theorem for imprimitivity systems and maximal decompositions of rational functions, Proc. Lond. Math. Soc. (3) 102 (2011), 1–24.Google Scholar
[Pak02]Pakovich, F., A counterexample to the ‘composition conjecture’, Proc. Amer. Math. Soc. 130 (2002), 3747–3749.CrossRefGoogle Scholar
[Pak03a]Pakovich, F., On the polynomial moment problem, Math. Res. Lett. 10 (2003), 401–410.CrossRefGoogle Scholar
[Pak03b]Pakovich, F., Polynomial moment problem, Mosc. Math. J. 3 (2003), Addendum to [Y. Yomdin, Center problem for Abel equation, compositions of functions and moment conditions, Mosc. Math. J. 3 (2003), 1167–1195].Google Scholar
[Pak04]Pakovich, F., On polynomials orthogonal to all powers of a Chebyshev polynomial on a segment, Israel J. Math 142 (2004), 273–283.Google Scholar
[Pak05]Pakovich, F., On polynomials orthogonal to all powers of a given polynomial on a segment, Bull. Sci. Math. 129 (2005), 749–774.Google Scholar
[Pak09]Pakovich, F., Prime and composite Laurent polynomials, Bull. Sci. Math. 133 (2009), 693–732.CrossRefGoogle Scholar
[PM09]Pakovich, F. and Muzychuk, M., Solution of the polynomial moment problem, Proc. Lond. Math. Soc. (3) 99 (2009), 633–657.Google Scholar
[PRY04]Pakovich, F., Roytvarf, N. and Yomdin, Y., Cauchy type integrals of algebraic functions, Israel J. Math. 144 (2004), 221–291.Google Scholar
[Rit22]Ritt, J., Prime and composite polynomials, Trans. Amer. Math. Soc. 23 (1922), 51–66.Google Scholar
[Roy01]Roytvarf, N., Generalized moments, composition of polynomials and Bernstein classes, in Entire functions in modern analysis: Boris Levin memorial conference, Israel Mathematical Conference Proceedings, vol. 15 (Bar-Ilan University, Ramat-Gan, Israel, 2001), 339–355.Google Scholar
[Sch82]Schinzel, A., Selected topics on polynomials (University of Michigan Press, Ann Arbor, MI, 1982).Google Scholar
[Tor88]Tortrat, P., Sur la composition des polynômes, Colloq. Math. 55 (1988), 329–353.Google Scholar
[Wie64]Wielandt, H., Finite permutation groups (Academic Press, Berlin, 1964).Google Scholar
[Yom03]Yomdin, Y., Center problem for Abel equation, compositions of functions and moment conditions, Mosc. Math. J. 3 (2003), 1167–1195.Google Scholar
[Zan93]Zannier, U., Ritt’s second theorem in arbitrary characteristic, J. Reine Angew. Math. 445 (1993), 175–203.Google Scholar
[ZM08]Zieve, M. and Müller, P., On Ritt’s polynomial decomposition theorem, Preprint (2008), math.AG/0807.3578v1.Google Scholar