Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-25T10:26:03.921Z Has data issue: false hasContentIssue false
  • English
  • Français

Gaudin subalgebras and stable rational curves

Part of: Representation theory of groups Lie algebras and Lie superalgebras Curves

Published online by Cambridge University Press:  26 April 2011

Leonardo Aguirre ,
Giovanni Felder  and
Alexander P. Veselov
Leonardo Aguirre
Affiliation:
Department of Mathematics, ETH Zurich, 8092 Zurich, Switzerland (email: [email protected])
Giovanni Felder
Affiliation:
Department of Mathematics, ETH Zurich, 8092 Zurich, Switzerland (email: [email protected])
Alexander P. Veselov
Affiliation:
Department of Mathematical Sciences, Loughborough University, Loughborough LE11 3TU, UK Moscow State University, Moscow 119899, Russia (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

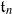Gaudin subalgebras are abelian Lie subalgebras of maximal dimension spanned by generators of the Kohno–Drinfeld Lie algebra . We show that Gaudin subalgebras form a variety isomorphic to the moduli space 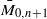of stable curves of genus zero with n+1 marked points. In particular, this gives an embedding of 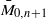in a Grassmannian of (n−1)-planes in an n(n−1)/2-dimensional space. We show that the sheaf of Gaudin subalgebras over 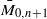is isomorphic to a sheaf of twisted first-order differential operators. For each representation of the Kohno–Drinfeld Lie algebra with fixed central character, we obtain a sheaf of commutative algebras whose spectrum is a coisotropic subscheme of a twisted version of the logarithmic cotangent bundle of .

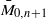Keywords

Gaudin modelsKohno–Drinfeld Lie algebrasstable curvesJucys–Murphy elements

MSC classification

Secondary: 14H10: Families, moduli (algebraic) 14H70: Relationships with integrable systems 17B99: None of the above, but in this section 20C30: Representations of finite symmetric groups
Type
Research Article
Information
Compositio Mathematica , Volume 147 , Issue 5 , September 2011 , pp. 1463 - 1478
Copyright
Copyright © Foundation Compositio Mathematica 2011

References

[Ati00]Atiyah, M., The geometry of classical particles, Surveys in Differential Geometry, vol. VII (International Press, Somerville, MA, 2000), 1–15; MR 1919420(2003h:55022).Google Scholar
[Ati01]Atiyah, M., Equivariant cohomology and representations of the symmetric group, Chin. Ann. Math. Ser. B 22 (2001), 23–30, doi: 10.1142/S0252959901000048; MR 1823127(2002b:20017).CrossRefGoogle Scholar
[AB02]Atiyah, M. and Bielawski, R., Nahm’s equations, configuration spaces and flag manifolds, Bull. Braz. Math. Soc. (N.S.) 33 (2002), 157–176; MR 1940347(2004f:53024).CrossRefGoogle Scholar
[CFR09]Chervov, A., Falqui, G. and Rybnikov, L., Limits of Gaudin systems: classical and quantum cases, SIGMA Symmetry Integrability Geom. Methods Appl. 5 (2009), Paper 029, 17; MR 2506183(2010f:82024).Google Scholar
[CFR10]Chervov, A., Falqui, G. and Rybnikov, L., Limits of Gaudin algebras, quantization of bending flows, Jucys–Murphy elements and Gelfand–Tsetlin bases, Lett. Math. Phys. 91 (2010), 129–150, doi: 10.1007/s11005-010-0371-y; MR 2586869.CrossRefGoogle Scholar
[Del70]Deligne, P., Équations différentielles à points singuliers réguliers, Lecture Notes in Mathematics, vol. 163 (Springer, Berlin, 1970), iii+133 (in French); MR 0417174(54#5232).CrossRefGoogle Scholar
[Dri90]Drinfel’d, V. G., On quasitriangular quasi-Hopf algebras and on a group that is closely connected with , Algebra i Analiz 2 (1990), 149–181 (in Russian); English transl., Leningrad Math. J., 2 (1991) 829–860; MR 1080203(92f:16047).Google Scholar
[FM03]Falqui, G. and Musso, F., Gaudin models and bending flows: a geometrical point of view, J. Phys. A 36 (2003), 11655–11676, doi: 10.1088/0305-4470/36/46/009; MR 2025867(2004i:37121).CrossRefGoogle Scholar
[FFR10]Feigin, B., Frenkel, E. and Rybnikov, L., Opers with irregular singularity and spectra of the shift of argument subalgebra, Duke Math. J. 155 (2010), 337–363, doi: 10.1215/00127094-2010-057.CrossRefGoogle Scholar
[FFT10]Feigin, B., Frenkel, E. and Toledano Laredo, V., Gaudin models with irregular singularities, Adv. Math. 223 (2010), 873–948, doi: 10.1016/j.aim.2009.09.007; MR 2565552.CrossRefGoogle Scholar
[Fre05]Frenkel, E., Gaudin model and opers, in Infinite dimensional algebras and quantum integrable systems, Progress in Mathematics, vol. 237 (Birkhäuser, Basel, 2005), 1–58; MR 2160841(2007e:17022).Google Scholar
[Gau76]Gaudin, M., Diagonalisation d’une classe d’Hamiltoniens de spin, J. Phys. 37 (1976), 1089–1098; (in French, with English summary); MR 0421442(54#9446).CrossRefGoogle Scholar
[Gau83]Gaudin, M., La fonction d’onde de Bethe, in Collection du Commissariat à l’Énergie Atomique: série Scientifique [Collection of the atomic energy commission: science series] (Masson, Paris, 1983), xvi+331 (in French); MR 693905(85h:82001).Google Scholar
[GHv88]Gerritzen, L., Herrlich, F. and van der Put, M., Stable n-pointed trees of projective lines, Indag. Math. (Proc.) 91 (1988), 131–163; MR 952512(89i:14005).CrossRefGoogle Scholar
[KM96]Kapovich, M. and Millson, J., The symplectic geometry of polygons in Euclidean space, J. Differential Geom. 44 (1996), 479–513; MR 1816048(2001m:53159).CrossRefGoogle Scholar
[Kap93]Kapranov, M. M., The permutoassociahedron, Mac Lane’s coherence theorem and asymptotic zones for the KZ equation, J. Pure Appl. Algebra 85 (1993), 119–142, doi: 10.1016/0022-4049(93)90049-Y; MR 1207505(94b:52017).Google Scholar
[Kee92]Keel, S., Intersection theory of moduli space of stable n-pointed curves of genus zero, Trans. Amer. Math. Soc. 330 (1992), 545–574; MR 1034665(92f:14003).Google Scholar
[Knu83]Knudsen, F. F., The projectivity of the moduli space of stable curves. II. The stacks Mg,n, Math. Scand. 52 (1983), 161–199; MR 702953(85d:14038a).Google Scholar
[Koh85]Kohno, T., Série de Poincaré–Koszul associée aux groupes de tresses pures, Invent. Math. 82 (1985), 57–75 (in French), doi: 10.1007/BF01394779; MR 808109(87c:32015a).Google Scholar
[Man76]Manakov, S. V., A remark on the integration of the Eulerian equations of the dynamics of an n-dimensional rigid body, Funksional. Anal. i Priložen. 10 (1976), 93–94 (in Russian); MR 0455031(56#13272).Google Scholar
[MTV09]Mukhin, E., Tarasov, V. and Varchenko, A., Schubert calculus and representations of the general linear group, J. Amer. Math. Soc. 22 (2009), 909–940, doi: 10.1090/S0894-0347-09-00640-7; MR 2525775.CrossRefGoogle Scholar
[MTVa]Mukhin, E., Tarasov, V. and Varchenko, A., Three sides of the geometric Langlands correspondence for gl N Gaudin model and Bethe vector averaging maps, available at arxiv.org/abs/0907.3266.Google Scholar
[MTVb]Mukhin, E., Tarasov, V. and Varchenko, A., Bethe algebra of the gl N+1 Gaudin model and algebra of functions on the critical set of the master function, available at arxiv.org/abs/0910.4690.Google Scholar
[OV96]Okounkov, A. and Vershik, A., A new approach to representation theory of symmetric groups, Selecta Math. (N.S.) 2 (1996), 581–605, doi: 10.1007/PL00001384; MR 1443185(99g:20024).CrossRefGoogle Scholar
[Red34]Rédei, L., Ein kombinatorischer Satz, Acta Litteraria Szeged 7 (1934), 3943.Google Scholar
[Uen08]Ueno, K., Conformal field theory with gauge symmetry, Fields Institute Monographs, vol. 24 (American Mathematical Society, Providence, RI, 2008); MR 2433154(2009k:81204).CrossRefGoogle Scholar
[VO04]Vershik, A. M. and Okun’kov, A. Yu., A new approach to representation theory of symmetric groups. II, Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 307 (2004), no. Teor. Predst. Din. Sist. Komb. i Algoritm. Metody. 10, 57–98, 281 (in Russian, with English and Russian summaries); English transl., J. Math. Sci. (N. Y.), 131, 2005, 5471–5494; MR 2050688(2005c:20024).CrossRefGoogle Scholar
[Vin90]Vinberg, E. B., Some commutative subalgebras of a universal enveloping algebra, Izv. Akad. Nauk SSSR Ser. Mat. 54 (1990), 3–25, 221, (in Russian); English transl., Math. USSR-Izv. 36 (1991) 1–22; MR 1044045(91b:17015).Google Scholar