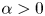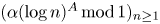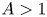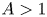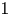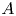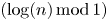1. Introduction
A sequence ![]() $(x(n))_{n\geq 1}\subseteq [0,1)$ is uniformly distributed modulo
$(x(n))_{n\geq 1}\subseteq [0,1)$ is uniformly distributed modulo ![]() $1$ if the proportion of points in any subinterval
$1$ if the proportion of points in any subinterval ![]() $I \subseteq [0,1)$ converges to the size of the interval:
$I \subseteq [0,1)$ converges to the size of the interval: ![]() $\#\{n\leq N:\ x(n)\in I\}\sim N|I|$, as
$\#\{n\leq N:\ x(n)\in I\}\sim N|I|$, as ![]() $N\rightarrow \infty$. The theory of uniform distribution dates back to 1916, to a seminal paper of Weyl [Reference WeylWey16], and constitutes a simple test of pseudo-randomness. A well-known result of Fejér (see [Reference Kuipers and NiederreiterKN74, p. 13]) implies that for any
$N\rightarrow \infty$. The theory of uniform distribution dates back to 1916, to a seminal paper of Weyl [Reference WeylWey16], and constitutes a simple test of pseudo-randomness. A well-known result of Fejér (see [Reference Kuipers and NiederreiterKN74, p. 13]) implies that for any ![]() $A>1$ and any
$A>1$ and any ![]() $\alpha >0$ the sequence
$\alpha >0$ the sequence
is uniformly distributed, while for ![]() $A=1$ the sequence is not uniformly distributed. In this paper, we study stronger, local tests for pseudo-randomness for this sequence.
$A=1$ the sequence is not uniformly distributed. In this paper, we study stronger, local tests for pseudo-randomness for this sequence.
Given an increasing ![]() $\mathbb {R}$-valued sequence,
$\mathbb {R}$-valued sequence, ![]() $(\omega (n))=(\omega (n))_{n>0}$, we denote the sequence modulo
$(\omega (n))=(\omega (n))_{n>0}$, we denote the sequence modulo ![]() $1$ by
$1$ by
Furthermore, let ![]() $u_N(n)\subset [0,1)$ denote the ordered sequence, thus
$u_N(n)\subset [0,1)$ denote the ordered sequence, thus ![]() $u_N(1) \le u_N(2) \le \dots \le u_N(N)$. With that, we define the gap distribution of
$u_N(1) \le u_N(2) \le \dots \le u_N(N)$. With that, we define the gap distribution of ![]() $(x(n))$ as the limiting distribution (if it exists): for
$(x(n))$ as the limiting distribution (if it exists): for ![]() $s>0$,
$s>0$,
where ![]() $\|\cdot \|$ denotes the distance to the nearest integer, and
$\|\cdot \|$ denotes the distance to the nearest integer, and ![]() $u_N(N+1)= u_N(1)$. Thus,
$u_N(N+1)= u_N(1)$. Thus, ![]() $P(s)$ represents the limiting proportion of (scaled) gaps between (spatially) neighboring elements in the sequence which are less than
$P(s)$ represents the limiting proportion of (scaled) gaps between (spatially) neighboring elements in the sequence which are less than ![]() $s$. We say that a sequence has Poissonian gap distribution if
$s$. We say that a sequence has Poissonian gap distribution if ![]() $P(s) = 1- e^{-s}$, the expected value for a uniformly distributed sequence on the unit interval.
$P(s) = 1- e^{-s}$, the expected value for a uniformly distributed sequence on the unit interval.

Figure 1. From left to right, the histograms represent the gap distribution density at time ![]() $N$ of
$N$ of ![]() $(\log n)_{n\geq 1}$,
$(\log n)_{n\geq 1}$, ![]() $((\log n)^{2})_{n > 0}$, and
$((\log n)^{2})_{n > 0}$, and ![]() $((\log n)^{3})_{n > 0}$ when
$((\log n)^{3})_{n > 0}$ when ![]() $N=10^{5}$ and the curve is the graph of
$N=10^{5}$ and the curve is the graph of ![]() $x \mapsto e^{-x}$. Note that
$x \mapsto e^{-x}$. Note that ![]() $(\log n)$ is not uniformly distributed, and the gap distribution is not Poissonian.
$(\log n)$ is not uniformly distributed, and the gap distribution is not Poissonian.
Our main theorem is the following result.
Theorem 1.1 Let ![]() $\omega (n):= \alpha ( \log n)^{A}$ for
$\omega (n):= \alpha ( \log n)^{A}$ for ![]() $A>1$ and any
$A>1$ and any ![]() $\alpha >0$. Then
$\alpha >0$. Then ![]() $x(n)$ has Poissonian gap distribution.
$x(n)$ has Poissonian gap distribution.
In fact, this theorem follows (via the method of moments) from Theorem 1.2 (below) which states that for every ![]() $m \ge 2$ the
$m \ge 2$ the ![]() $m$-point correlation function of this sequence is Poissonian. By that we mean the following. Let
$m$-point correlation function of this sequence is Poissonian. By that we mean the following. Let ![]() $m\geq 2$ be an integer, and let
$m\geq 2$ be an integer, and let ![]() $f \in C_c^\infty (\mathbb {R}^{m-1})$ be a compactly supported function which can be thought of as a stand-in for the characteristic function of a Cartesian product of compact intervals in
$f \in C_c^\infty (\mathbb {R}^{m-1})$ be a compactly supported function which can be thought of as a stand-in for the characteristic function of a Cartesian product of compact intervals in ![]() $\mathbb {R}^{m-1}$. Let
$\mathbb {R}^{m-1}$. Let ![]() $[N]:=\{1,\ldots,N\}$ and define the
$[N]:=\{1,\ldots,N\}$ and define the ![]() $m$-point correlation of
$m$-point correlation of ![]() $(x(n))$, at time
$(x(n))$, at time ![]() $N$, to be
$N$, to be
 \begin{equation} R^{(m)}(N,f) := \frac{1}{N}\sum_{\boldsymbol{\mathbf{n}} \in [N]^m}^\ast f(N\|x(n_1)-x(n_2)\|,N \|x(n_2)-x(n_3)\|, \ldots, N\|x(n_{m-1})-x(n_{m})\|), \end{equation}
\begin{equation} R^{(m)}(N,f) := \frac{1}{N}\sum_{\boldsymbol{\mathbf{n}} \in [N]^m}^\ast f(N\|x(n_1)-x(n_2)\|,N \|x(n_2)-x(n_3)\|, \ldots, N\|x(n_{m-1})-x(n_{m})\|), \end{equation}
where ![]() $\sum \limits ^\ast$ denotes a sum over distinct
$\sum \limits ^\ast$ denotes a sum over distinct ![]() $m$-tuples. Thus, the
$m$-tuples. Thus, the ![]() $m$-point correlation measures how correlated points are on the scale of the average gap between neighboring points (which is
$m$-point correlation measures how correlated points are on the scale of the average gap between neighboring points (which is ![]() $N^{-1}$). We say that
$N^{-1}$). We say that ![]() $(x(n))$ has Poissonian
$(x(n))$ has Poissonian ![]() $m$-point correlation if
$m$-point correlation if
That is, if the ![]() $m$-point correlation converges to the expected value if the sequence was uniformly distributed on the unit interval.
$m$-point correlation converges to the expected value if the sequence was uniformly distributed on the unit interval.
Theorem 1.2 Let ![]() $\omega (n):= \alpha (\log n)^{A}$ for
$\omega (n):= \alpha (\log n)^{A}$ for ![]() $A>1$ and any
$A>1$ and any ![]() $\alpha >0$. Then
$\alpha >0$. Then ![]() $x(n)$ has Poissonian
$x(n)$ has Poissonian ![]() $m$-level correlations for all
$m$-level correlations for all ![]() $m \ge 2$.
$m \ge 2$.
It should be noted that Theorem 1.2 is far stronger than Theorem 1.1. In addition to the gap distribution, Theorem 1.2 allows us to recover a wide variety of statistics such as the ![]() $i$th nearest neighbor distribution for any
$i$th nearest neighbor distribution for any ![]() $i \ge 1$.
$i \ge 1$.
For our analysis, it is more useful to have good control on the support of the Fourier transform of ![]() $f$, and not crucial that
$f$, and not crucial that ![]() $f$ be compactly supported. Thus, we restate Theorem 1.2 here for this class of
$f$ be compactly supported. Thus, we restate Theorem 1.2 here for this class of ![]() $f$. We prove that Theorem 1.2 follows from Theorem 1.3 in § 8.
$f$. We prove that Theorem 1.2 follows from Theorem 1.3 in § 8.
Theorem 1.3 Let ![]() $\omega (n):=\alpha (\log n)^A$ for
$\omega (n):=\alpha (\log n)^A$ for ![]() $A>1$ and any
$A>1$ and any ![]() $\alpha > 0$. Then, for any
$\alpha > 0$. Then, for any ![]() $m \ge 2$, we have
$m \ge 2$, we have
for any positive function ![]() $f \in C^\infty (\mathbb {R}^{m-1})$, whose Fourier transform
$f \in C^\infty (\mathbb {R}^{m-1})$, whose Fourier transform ![]() $\widehat {f}$ has compact support.
$\widehat {f}$ has compact support.
Here we use ![]() $\widehat {f}$ to denote the Fourier transform of
$\widehat {f}$ to denote the Fourier transform of ![]() $f$. To avoid carrying a constant through we assume the support of
$f$. To avoid carrying a constant through we assume the support of ![]() $\widehat {f}$ is contained in
$\widehat {f}$ is contained in ![]() $(-1,1)$.
$(-1,1)$.
Previous work
The study of the uniform distribution and fine-scale local statistics of sequences modulo ![]() $1$ has a long history which we outlined in more detail in a previous paper [Reference Lutsko, Sourmelidis and TechnauLST24]. If we consider the sequence
$1$ has a long history which we outlined in more detail in a previous paper [Reference Lutsko, Sourmelidis and TechnauLST24]. If we consider the sequence ![]() $(\alpha n^\theta \,\mathrm {mod}\,1)_{n\geq 1}$, there have been many attempts to understand the local statistics, in particular the pair correlation (when
$(\alpha n^\theta \,\mathrm {mod}\,1)_{n\geq 1}$, there have been many attempts to understand the local statistics, in particular the pair correlation (when ![]() $m=2$). It is known that for any
$m=2$). It is known that for any ![]() $\theta \neq 1$, if
$\theta \neq 1$, if ![]() $\alpha$ belongs to a set of full measure, then the pair correlation function is Poissonian [Reference Rudnick and SarnakRS98, Reference Aistleitner, El-Baz and MunschAEM21, Reference Rudnick and TechnauRT22]. However, there are very few explicit (i.e. non-metric) results. When
$\alpha$ belongs to a set of full measure, then the pair correlation function is Poissonian [Reference Rudnick and SarnakRS98, Reference Aistleitner, El-Baz and MunschAEM21, Reference Rudnick and TechnauRT22]. However, there are very few explicit (i.e. non-metric) results. When ![]() $\theta = 2$ Heath-Brown [Reference Heath-BrownHea10] gave an algorithmic construction of certain
$\theta = 2$ Heath-Brown [Reference Heath-BrownHea10] gave an algorithmic construction of certain ![]() $\alpha$ for which the pair correlation is Poissonian; however, this construction did not give an exact number. When
$\alpha$ for which the pair correlation is Poissonian; however, this construction did not give an exact number. When ![]() $\theta = 1/2$ and
$\theta = 1/2$ and ![]() $\alpha ^2 \in \mathbb {Q}$ the problem lends itself to tools from homogeneous dynamics. This was exploited by Elkies and McMullen [Reference Elkies and McMullenEM04] who showed that the gap distribution is not Poissonian, and by El-Baz, Marklof, Vinogradov [Reference El-Baz, Marklof and VinogradovEMV15] who showed that the sequence
$\alpha ^2 \in \mathbb {Q}$ the problem lends itself to tools from homogeneous dynamics. This was exploited by Elkies and McMullen [Reference Elkies and McMullenEM04] who showed that the gap distribution is not Poissonian, and by El-Baz, Marklof, Vinogradov [Reference El-Baz, Marklof and VinogradovEMV15] who showed that the sequence ![]() $(\alpha n^{1/2}\, \mathrm {mod}\,1)_{n\in \mathbb {N} \setminus \square }$, where
$(\alpha n^{1/2}\, \mathrm {mod}\,1)_{n\in \mathbb {N} \setminus \square }$, where ![]() $\square$ denotes the set of squares, does have Poissonian pair correlation.
$\square$ denotes the set of squares, does have Poissonian pair correlation.
With these sparse exceptions, the only explicit results occur when the exponent ![]() $\theta$ is small. If
$\theta$ is small. If ![]() $\theta \le 14/41$ the authors and Sourmelidis [Reference Lutsko, Sourmelidis and TechnauLST24] showed that the pair correlation function is Poissonian for all values of
$\theta \le 14/41$ the authors and Sourmelidis [Reference Lutsko, Sourmelidis and TechnauLST24] showed that the pair correlation function is Poissonian for all values of ![]() $\alpha >0$. This was later extended by the authors [Reference Lutsko and TechnauLT21] to show that these monomial sequences exhibit Poissonian
$\alpha >0$. This was later extended by the authors [Reference Lutsko and TechnauLT21] to show that these monomial sequences exhibit Poissonian ![]() $m$-point correlations (for
$m$-point correlations (for ![]() $m\geq 3$) for any
$m\geq 3$) for any ![]() $\alpha >0$ if
$\alpha >0$ if ![]() $\theta < 1/(m^2+m-1)$. To the best of our knowledge the former is the only explicit result proving Poissonian pair correlations for sequences modulo
$\theta < 1/(m^2+m-1)$. To the best of our knowledge the former is the only explicit result proving Poissonian pair correlations for sequences modulo ![]() $1$, and the latter result is the only result proving convergence of the higher-order correlations to any limit.
$1$, and the latter result is the only result proving convergence of the higher-order correlations to any limit.
The authors’ previous work motivates the natural question: what about sequences which grow slower than any power of ![]() $n$? It is natural to hypothesize that such sequences might exhibit Poissonian
$n$? It is natural to hypothesize that such sequences might exhibit Poissonian ![]() $m$-point correlations for all
$m$-point correlations for all ![]() $m$. However, there is a constraint. Marklof and Strömbergsson [Reference Marklof and StrömbergssonMS13] have shown that the gap distribution of
$m$. However, there is a constraint. Marklof and Strömbergsson [Reference Marklof and StrömbergssonMS13] have shown that the gap distribution of ![]() $( (\log n)/(\log b) \,\mathrm {mod}\, 1)_{n\geq 1}$ exists for
$( (\log n)/(\log b) \,\mathrm {mod}\, 1)_{n\geq 1}$ exists for ![]() $b>1$, and is not Poissonian (thus the correlations cannot all be Poissonian). However, they also showed that in the limit as
$b>1$, and is not Poissonian (thus the correlations cannot all be Poissonian). However, they also showed that in the limit as ![]() $b$ tends to
$b$ tends to ![]() $1$, this limiting distribution converges to the Poissonian distribution (see [Reference Marklof and StrömbergssonMS13, (74)]). Thus, the natural question becomes: what can be said about sequences growing faster than
$1$, this limiting distribution converges to the Poissonian distribution (see [Reference Marklof and StrömbergssonMS13, (74)]). Thus, the natural question becomes: what can be said about sequences growing faster than ![]() $\log (n)$ but slower than any power of
$\log (n)$ but slower than any power of ![]() $n$?
$n$?
With that context in mind, our result has several implications. First, it provides the only example at present of an explicit sequence whose ![]() $m$-point correlations can be shown to converge to the Poissonian limit (and thus whose gap distribution is Poissonian). Second, it answers the natural question implied by our previous work on monomial sequences. Finally, it answers the natural question implied by Marklof and Strömbergsson's result on logarithmic sequences.
$m$-point correlations can be shown to converge to the Poissonian limit (and thus whose gap distribution is Poissonian). Second, it answers the natural question implied by our previous work on monomial sequences. Finally, it answers the natural question implied by Marklof and Strömbergsson's result on logarithmic sequences.
1.1 Plan of the paper
The proof of Theorem 1.2 adds several new ideas to the method developed in [Reference Lutsko and TechnauLT21], which is insufficient for the definitive results established here. Broadly, we argue in three steps, detailing the difficulties and innovations in each step.
In the remainder of this work we take ![]() $\alpha = 1$; exactly the same proof applies to general
$\alpha = 1$; exactly the same proof applies to general ![]() $\alpha$, leaving straightforward adaptations aside. Fix
$\alpha$, leaving straightforward adaptations aside. Fix ![]() $m \ge 2$ and assume the sequence has Poissonian
$m \ge 2$ and assume the sequence has Poissonian ![]() $j$-point correlation for
$j$-point correlation for ![]() $2\le j< m$.
$2\le j< m$.
Step 1. Remove the distinctness condition in the ![]() $m$-point correlation by relating the completed correlation to the
$m$-point correlation by relating the completed correlation to the ![]() $m$th moment of a random variable. This will add a new frequency variable, with the benefit of decorrelating the sequence elements. Then we perform a Fourier decomposition of this moment and, using a combinatorial argument from [Reference Lutsko and TechnauLT21, § 3], we reduce the problem of convergence for the moment to convergence of one particular term to an explicit ‘target’. This step works quite similarly to what we did in [Reference Lutsko and TechnauLT21].
$m$th moment of a random variable. This will add a new frequency variable, with the benefit of decorrelating the sequence elements. Then we perform a Fourier decomposition of this moment and, using a combinatorial argument from [Reference Lutsko and TechnauLT21, § 3], we reduce the problem of convergence for the moment to convergence of one particular term to an explicit ‘target’. This step works quite similarly to what we did in [Reference Lutsko and TechnauLT21].
Step 2. Using various partitions of unity, we further reduce the problem to an asymptotic evaluation of the ![]() $L^m([0,1])$-norm of a two-dimensional exponential sum. Then we apply van der Corput's
$L^m([0,1])$-norm of a two-dimensional exponential sum. Then we apply van der Corput's ![]() $B$-process to each of these variables. In contrast to our argument in [Reference Lutsko and TechnauLT21], we can no longer use the form of the sequence to perform explicit computations throughout. Instead, a more fundamental understanding of how the two
$B$-process to each of these variables. In contrast to our argument in [Reference Lutsko and TechnauLT21], we can no longer use the form of the sequence to perform explicit computations throughout. Instead, a more fundamental understanding of how the two ![]() $B$-processes work is now required. In fact, after the first application of the
$B$-processes work is now required. In fact, after the first application of the ![]() $B$-process we end up with an implicitly defined phase function. Surprisingly, after the second application of the
$B$-process we end up with an implicitly defined phase function. Surprisingly, after the second application of the ![]() $B$-process (in the other variable) we can show that a manageable phase function arises! This is the content of Lemma 4.10, and we believe this by-product of our investigation to be of some independent interest. Being able to understand the phase function arising is crucial to performing the next step. Furthermore, a simple computation yields that if we stop at this step and apply the triangle inequality the resulting error term is of size
$B$-process (in the other variable) we can show that a manageable phase function arises! This is the content of Lemma 4.10, and we believe this by-product of our investigation to be of some independent interest. Being able to understand the phase function arising is crucial to performing the next step. Furthermore, a simple computation yields that if we stop at this step and apply the triangle inequality the resulting error term is of size ![]() $O((\log N)^{(A+1)m})$.
$O((\log N)^{(A+1)m})$.
Step 3. Finally, we expand the ![]() $L^m([0,1])$-norm giving an oscillatory integral. Then, using a localized version of Van der Corput's lemma, we achieve an extra saving to bound the error term by
$L^m([0,1])$-norm giving an oscillatory integral. Then, using a localized version of Van der Corput's lemma, we achieve an extra saving to bound the error term by ![]() $o(1)$. In [Reference Lutsko and TechnauLT21] we used classical theorems from linear algebra to justify that that localized version of Van der Corput's lemma is applicable, by showing that Wronskians of a family of relevant curves are uniformly bounded from below. In the present situation, the underlying geometry and Wronskians are considerably more involved. After several initial manipulations we boil matters down to determinants of generalized Vandermonde matrices. To handle those we rely on recent work of Khare and Tao [Reference Khare and TaoKT21], which is precise enough to (by a small logarithmic gain) single out the largest contribution to the Wronskian and thereby complete the argument.
$o(1)$. In [Reference Lutsko and TechnauLT21] we used classical theorems from linear algebra to justify that that localized version of Van der Corput's lemma is applicable, by showing that Wronskians of a family of relevant curves are uniformly bounded from below. In the present situation, the underlying geometry and Wronskians are considerably more involved. After several initial manipulations we boil matters down to determinants of generalized Vandermonde matrices. To handle those we rely on recent work of Khare and Tao [Reference Khare and TaoKT21], which is precise enough to (by a small logarithmic gain) single out the largest contribution to the Wronskian and thereby complete the argument.
Notation
Throughout, we use the usual Bachmann–Landau notation: for functions ![]() $f,g:X \rightarrow \mathbb {R}$, defined on some set
$f,g:X \rightarrow \mathbb {R}$, defined on some set ![]() $X$, we write
$X$, we write ![]() $f \ll g$ (or
$f \ll g$ (or ![]() $f=O(g)$) to denote that there exists a constant
$f=O(g)$) to denote that there exists a constant ![]() $C>0$ such that
$C>0$ such that ![]() $\vert f(x)\vert \leq C \vert g(x) \vert$ for all
$\vert f(x)\vert \leq C \vert g(x) \vert$ for all ![]() $x\in X$. Moreover, let
$x\in X$. Moreover, let ![]() $f\asymp g$ denote
$f\asymp g$ denote ![]() $f \ll g$ and
$f \ll g$ and ![]() $g \ll f$, and let
$g \ll f$, and let ![]() $f = o(g)$ denote that
$f = o(g)$ denote that ![]() $\frac {f(x)}{g(x)} \to 0$.
$\frac {f(x)}{g(x)} \to 0$.
Given a Schwartz function ![]() $f: \mathbb {R}^m \to \mathbb {R}$, let
$f: \mathbb {R}^m \to \mathbb {R}$, let ![]() $\widehat {f}$ denote the
$\widehat {f}$ denote the ![]() $m$-dimensional Fourier transform:
$m$-dimensional Fourier transform:
Here, and throughout we let ![]() $e(x):= e^{2\pi i x}$. Moreover, we use the convention
$e(x):= e^{2\pi i x}$. Moreover, we use the convention ![]() $\frac {0}{0}=0$ to avoid extra conditions on summations.
$\frac {0}{0}=0$ to avoid extra conditions on summations.
All of the sums which appear range over integers, in the indicated interval. We will frequently be taking sums over multiple variables, thus if ![]() $\boldsymbol {\mathbf {u}}$ is an
$\boldsymbol {\mathbf {u}}$ is an ![]() $m$-dimensional vector, for brevity, we write
$m$-dimensional vector, for brevity, we write
Moreover, all ![]() $L^p$ norms are taken with respect to Lebesgue measure; we often do not include the domain when it is obvious. Let
$L^p$ norms are taken with respect to Lebesgue measure; we often do not include the domain when it is obvious. Let
For ease of notation, ![]() $\varepsilon >0$ may vary from line to line by a bounded constant.
$\varepsilon >0$ may vary from line to line by a bounded constant.
2. Preliminaries
The following stationary phase principle is derived from the work of Blomer, Khan and Young [Reference Blomer, Khan and YoungBKY13, Proposition 8.2]. In application we will not make use of the full asymptotic expansion, but this will give us a particularly good error term which is essential to our argument.
Proposition 2.1 (Stationary phase expansion)
Let ![]() $w\in C_{c}^{\infty }(\mathbb {R})$ be supported in a compact interval
$w\in C_{c}^{\infty }(\mathbb {R})$ be supported in a compact interval ![]() $J$ of length
$J$ of length ![]() $\Omega _w>0$ so that there exists an
$\Omega _w>0$ so that there exists an ![]() $\Lambda _w>0$ for which
$\Lambda _w>0$ for which
for all ![]() $j\in \mathbb {N}$. Suppose
$j\in \mathbb {N}$. Suppose ![]() $\psi$ is a smooth function on
$\psi$ is a smooth function on ![]() $J$ so that there exists a unique critical point
$J$ so that there exists a unique critical point ![]() $x_{0}$ with
$x_{0}$ with ![]() $\psi '(x_{0})=0$. Suppose there exist values
$\psi '(x_{0})=0$. Suppose there exist values ![]() $\Lambda _{\psi }>0$ and
$\Lambda _{\psi }>0$ and ![]() $\Omega _\psi >0$ such that
$\Omega _\psi >0$ such that
for all ![]() $j > 2$. Moreover, let
$j > 2$. Moreover, let ![]() $\delta \in (0,1/10)$, and
$\delta \in (0,1/10)$, and ![]() $Z:=\Omega _w + \Omega _{\psi }+\Lambda _w+\Lambda _{\psi }+1$. If
$Z:=\Omega _w + \Omega _{\psi }+\Lambda _w+\Lambda _{\psi }+1$. If
 \begin{equation} \Lambda_{\psi}\geq Z^{3\delta}\quad \mathrm{and}\quad \Omega_w\geq\frac{\Omega_{\psi}Z^{\frac{\delta}{2}}}{\Lambda_{\psi}^{1/2}}\end{equation}
\begin{equation} \Lambda_{\psi}\geq Z^{3\delta}\quad \mathrm{and}\quad \Omega_w\geq\frac{\Omega_{\psi}Z^{\frac{\delta}{2}}}{\Lambda_{\psi}^{1/2}}\end{equation}hold, then
has the asymptotic expansion
 \[ I=\frac{e(\psi(x_{0}))}{\sqrt{\psi''(x_{0})}} \sum_{0\leq j \leq3C/\delta}p_{j}(x_{0})+O_{C,\delta}(Z^{-C}) \]
\[ I=\frac{e(\psi(x_{0}))}{\sqrt{\psi''(x_{0})}} \sum_{0\leq j \leq3C/\delta}p_{j}(x_{0})+O_{C,\delta}(Z^{-C}) \]
for any fixed ![]() $C\in \mathbb {Z}_{\geq 1}$; here
$C\in \mathbb {Z}_{\geq 1}$; here
where
In a slightly simpler form we have the following lemma.
Lemma 2.2 (First-order stationary phase)
Let ![]() $\psi$ and
$\psi$ and ![]() $w$ be smooth, real-valued functions defined on a compact interval
$w$ be smooth, real-valued functions defined on a compact interval ![]() $[a, b]$. Let
$[a, b]$. Let ![]() $w(a) = w(b) = 0$. Suppose there exist constants
$w(a) = w(b) = 0$. Suppose there exist constants ![]() $\Lambda _\psi,\Omega _w,\Omega _\psi \geq 3$ satisfying (2.1), with
$\Lambda _\psi,\Omega _w,\Omega _\psi \geq 3$ satisfying (2.1), with ![]() $Z$ as in Proposition 2.1 and
$Z$ as in Proposition 2.1 and ![]() $\Lambda _w=1$ so that
$\Lambda _w=1$ so that
 \begin{equation} \psi^{(j)}(x) \ll \frac{\Lambda_\psi}{ \Omega_\psi^j},\quad w^{(j)} (x)\ll \frac{1}{\Omega_w^j}\quad \text{and}\quad \psi^{(2)} (x)\gg \frac{\Lambda_\psi}{\Omega_\psi^2} \end{equation}
\begin{equation} \psi^{(j)}(x) \ll \frac{\Lambda_\psi}{ \Omega_\psi^j},\quad w^{(j)} (x)\ll \frac{1}{\Omega_w^j}\quad \text{and}\quad \psi^{(2)} (x)\gg \frac{\Lambda_\psi}{\Omega_\psi^2} \end{equation}
for all ![]() $j=0,1,2,\ldots$ and all
$j=0,1,2,\ldots$ and all ![]() $x\in [a,b]$. If
$x\in [a,b]$. If ![]() $\psi ^\prime (x_0)=0$ for a unique
$\psi ^\prime (x_0)=0$ for a unique ![]() $x_0\in [a,b]$, and if
$x_0\in [a,b]$, and if ![]() $\psi ^{(2)}(x)>0$, then
$\psi ^{(2)}(x)>0$, then
 \[ \int_{a}^{b} w(x) e(\psi(x)) \,d x = \frac{e(\psi(x_0) + 1/8)}{\sqrt{|\psi^{(2)}(x_0)|}} w(x_0) + O\bigg(\frac{\Omega_\psi^3}{\Lambda_{\psi}^{3/2}\Omega_w^2} + \frac{1}{Z}\bigg). \]
\[ \int_{a}^{b} w(x) e(\psi(x)) \,d x = \frac{e(\psi(x_0) + 1/8)}{\sqrt{|\psi^{(2)}(x_0)|}} w(x_0) + O\bigg(\frac{\Omega_\psi^3}{\Lambda_{\psi}^{3/2}\Omega_w^2} + \frac{1}{Z}\bigg). \]
If instead ![]() $\psi ^{(2)}(x)<0$ on
$\psi ^{(2)}(x)<0$ on ![]() $[a,b]$ then the same equation holds with
$[a,b]$ then the same equation holds with ![]() $e(\psi (x_0) + 1/8)$ replaced by
$e(\psi (x_0) + 1/8)$ replaced by ![]() $e(\psi (x_0) - 1/8)$.
$e(\psi (x_0) - 1/8)$.
Proof. We apply Proposition 2.1 with ![]() $\Lambda _w=1$ and
$\Lambda _w=1$ and ![]() $C=1$. In which case the first error term comes from the term
$C=1$. In which case the first error term comes from the term ![]() $p_1$ in the expansion. All higher-order terms give a smaller contribution; see [Reference Blomer, Khan and YoungBKY13, p. 20] for a more detailed explanation.
$p_1$ in the expansion. All higher-order terms give a smaller contribution; see [Reference Blomer, Khan and YoungBKY13, p. 20] for a more detailed explanation.
Moreover, we also need the following version of van der Corput's lemma. ([Reference SteinSte93, Chapter VIII, Proposition 2]).
Lemma 2.3 (van der Corput's lemma)
Let ![]() $[a,b]$ be a compact interval. Let
$[a,b]$ be a compact interval. Let ![]() $\psi,w:[a,b]\rightarrow \mathbb {R}$ be smooth functions. Assume
$\psi,w:[a,b]\rightarrow \mathbb {R}$ be smooth functions. Assume ![]() $\psi ''$ does not change sign on
$\psi ''$ does not change sign on ![]() $[a,b]$ and that for some
$[a,b]$ and that for some ![]() $j\geq 1$ and
$j\geq 1$ and ![]() $\Lambda >0$ the bound
$\Lambda >0$ the bound
holds for all ![]() $x\in [a,b]$. Then
$x\in [a,b]$. Then
where the implied constant depends only on ![]() $j$.
$j$.
Generalized Vandermonde matrices
One of the primary difficulties which we will encounter in § 6 is the fact that taking derivatives of exponentials (which arise as the inverse of the ![]() $\log$s defining our sequence) increases in complexity as we take derivatives. To handle this we appeal to a recent result of Khare and Tao [Reference Khare and TaoKT21] which requires us to set up some notation. Given an
$\log$s defining our sequence) increases in complexity as we take derivatives. To handle this we appeal to a recent result of Khare and Tao [Reference Khare and TaoKT21] which requires us to set up some notation. Given an ![]() $M$-tuple
$M$-tuple ![]() $\boldsymbol {\mathbf {u}} \in \mathbb {R}^M$, let
$\boldsymbol {\mathbf {u}} \in \mathbb {R}^M$, let
denote the Vandermonde determinant. Furthermore, given two tuples ![]() $\boldsymbol {\mathbf {u}}$ and
$\boldsymbol {\mathbf {u}}$ and ![]() $\boldsymbol {\mathbf {n}}$, we define
$\boldsymbol {\mathbf {n}}$, we define
 \[ \boldsymbol{\mathbf{u}}^{\boldsymbol{\mathbf{n}}} := u_1^{n_1} \cdots u_M^{n_M}\quad \mbox{and}\quad \boldsymbol{\mathbf{u}}^{\circ\boldsymbol{\mathbf{n}}} := \begin{pmatrix} u_1^{n_1} & u_1^{n_2} & \cdots & u_1^{n_M}\\ u_2^{n_1} & u_2^{n_2} & \cdots & u_2^{n_M}\\ \vdots & \vdots & \vdots & \vdots \\ u_M^{n_1} & u_M^{n_2} & \cdots & u_M^{n_M} \end{pmatrix}, \]
\[ \boldsymbol{\mathbf{u}}^{\boldsymbol{\mathbf{n}}} := u_1^{n_1} \cdots u_M^{n_M}\quad \mbox{and}\quad \boldsymbol{\mathbf{u}}^{\circ\boldsymbol{\mathbf{n}}} := \begin{pmatrix} u_1^{n_1} & u_1^{n_2} & \cdots & u_1^{n_M}\\ u_2^{n_1} & u_2^{n_2} & \cdots & u_2^{n_M}\\ \vdots & \vdots & \vdots & \vdots \\ u_M^{n_1} & u_M^{n_2} & \cdots & u_M^{n_M} \end{pmatrix}, \]
the latter being a generalized Vandermonde matrix. Finally, let ![]() $\boldsymbol {\mathbf {n}}_{\min } :=(0,1, \ldots, M-1)$. Then Khare and Tao established the following lemma.
$\boldsymbol {\mathbf {n}}_{\min } :=(0,1, \ldots, M-1)$. Then Khare and Tao established the following lemma.
Lemma 2.4 [Reference Khare and TaoKT21, Lemma 5.3]
Let ![]() $K$ be a compact subset of the cone
$K$ be a compact subset of the cone
Then there exist constants ![]() $C,c>0$ such that
$C,c>0$ such that
for all ![]() $\boldsymbol {\mathbf {u}} \in (0,\infty )^M$ with
$\boldsymbol {\mathbf {u}} \in (0,\infty )^M$ with ![]() $u_1 \le \dots \le u_M$ and all
$u_1 \le \dots \le u_M$ and all ![]() $\boldsymbol {\mathbf {n}} \in K$.
$\boldsymbol {\mathbf {n}} \in K$.
3. Combinatorial completion
The proof of Theorem 1.3 follows an inductive argument. Thus, fix ![]() $m \ge 2$ and assume
$m \ge 2$ and assume ![]() $(x(n))$ has
$(x(n))$ has ![]() $j$-point correlations for all
$j$-point correlations for all ![]() $j < m$. Let
$j < m$. Let ![]() $f$ be a positive
$f$ be a positive ![]() $C^\infty (\mathbb {R})$ function with
$C^\infty (\mathbb {R})$ function with ![]() $\widehat {f} \in C_c^\infty (\mathbb {R})$, and define
$\widehat {f} \in C_c^\infty (\mathbb {R})$, and define
Note that if ![]() $f$ was the indicator function of an interval
$f$ was the indicator function of an interval ![]() $I$, then
$I$, then ![]() $S_N$ would count the number of points in
$S_N$ would count the number of points in ![]() $(x_n)_{n \le N}$ which land in the shifted interval
$(x_n)_{n \le N}$ which land in the shifted interval ![]() $I/N+s/N$. Now consider the
$I/N+s/N$. Now consider the ![]() $m$th moment of
$m$th moment of ![]() $S_N$. Then one can show that (see [Reference Lutsko and TechnauLT21, § 3])
$S_N$. Then one can show that (see [Reference Lutsko and TechnauLT21, § 3])
 \begin{align}
\mathcal{M}^{(m)}(N) &:= \int_0^1 S_N(s,f)^m \,{d}s \nonumber\\
&\; = \int_0^1 \sum_{\boldsymbol{\mathbf{n}} \in [N]^m}\sum_{\boldsymbol{\mathbf{k}} \in \mathbb{Z}^m}
f(N(\omega(n_1)+k_1 + s)) \cdots f(N(\omega(n_m) +k_m + s))\,{d} s \nonumber\\
&\; = \frac{1}{N}\sum_{\boldsymbol{\mathbf{n}} \in [N]^m}\sum_{\boldsymbol{\mathbf{k}}\in \mathbb{Z}^{m-1}}
F(N(\omega(n_1)-\omega(n_2) +k_1),\ldots N(\omega(n_{m-1})-\omega(n_m) +k_{m-1})),
\end{align}
\begin{align}
\mathcal{M}^{(m)}(N) &:= \int_0^1 S_N(s,f)^m \,{d}s \nonumber\\
&\; = \int_0^1 \sum_{\boldsymbol{\mathbf{n}} \in [N]^m}\sum_{\boldsymbol{\mathbf{k}} \in \mathbb{Z}^m}
f(N(\omega(n_1)+k_1 + s)) \cdots f(N(\omega(n_m) +k_m + s))\,{d} s \nonumber\\
&\; = \frac{1}{N}\sum_{\boldsymbol{\mathbf{n}} \in [N]^m}\sum_{\boldsymbol{\mathbf{k}}\in \mathbb{Z}^{m-1}}
F(N(\omega(n_1)-\omega(n_2) +k_1),\ldots N(\omega(n_{m-1})-\omega(n_m) +k_{m-1})),
\end{align}
where
 \begin{align*} & F(z_1,z_2, \ldots, z_{m-1}) \\ &\quad := \int_{\mathbb{R}} f(s)f(z_1+z_2+\cdots + z_{m-1}+s) f(z_2+\cdots + z_{m-1}+s)\cdots f(z_{m-1}+s)\,d s. \end{align*}
\begin{align*} & F(z_1,z_2, \ldots, z_{m-1}) \\ &\quad := \int_{\mathbb{R}} f(s)f(z_1+z_2+\cdots + z_{m-1}+s) f(z_2+\cdots + z_{m-1}+s)\cdots f(z_{m-1}+s)\,d s. \end{align*}
As such we can relate the ![]() $m$th moment of
$m$th moment of ![]() $S_N$ to the
$S_N$ to the ![]() $m$-point correlation of
$m$-point correlation of ![]() $F$. Note that since
$F$. Note that since ![]() $\widehat {f}$ has compact support,
$\widehat {f}$ has compact support, ![]() $\widehat {F}$ also has compact support. To recover the
$\widehat {F}$ also has compact support. To recover the ![]() $m$-point correlation in full generality, we replace the moment
$m$-point correlation in full generality, we replace the moment ![]() $\int S_N(s,f)^m \,{d}s$ with the mixed moment
$\int S_N(s,f)^m \,{d}s$ with the mixed moment ![]() $\int \prod _{i=1}^m S_N(s,f_i) \,{d} s$ for some collection of
$\int \prod _{i=1}^m S_N(s,f_i) \,{d} s$ for some collection of ![]() $f_i:\mathbb {R}\to \mathbb {R}$. The proof below can be applied in this generality; however, for ease of notation we only explain the details in the former case.
$f_i:\mathbb {R}\to \mathbb {R}$. The proof below can be applied in this generality; however, for ease of notation we only explain the details in the former case.
3.1 Combinatorial target
We will need the following combinatorial definitions to explain how to prove convergence of the ![]() $m$-point correlation from (3.1). Given a partition
$m$-point correlation from (3.1). Given a partition ![]() $\mathcal {P}$ of
$\mathcal {P}$ of ![]() $[ m]$, we say that
$[ m]$, we say that ![]() $j\in [m]$ is isolated if
$j\in [m]$ is isolated if ![]() $j$ belongs to a partition element of size
$j$ belongs to a partition element of size ![]() $1$. A partition is called non-isolating if no element is isolated (and otherwise we say it is isolating). For our example
$1$. A partition is called non-isolating if no element is isolated (and otherwise we say it is isolating). For our example ![]() $\mathcal {P} = \{\{1,3\}, \{4\}, \{2,5,6\}\}$ we have that
$\mathcal {P} = \{\{1,3\}, \{4\}, \{2,5,6\}\}$ we have that ![]() $4$ is isolated, and thus
$4$ is isolated, and thus ![]() $\mathcal {P}$ is isolating.
$\mathcal {P}$ is isolating.
Now consider the middle line of (3.1). We apply Poisson summation to each of the ![]() $k_i$ sums. That is, we insert
$k_i$ sums. That is, we insert
 \begin{equation} \sum_{k \in \mathbb{Z}} f(N(\omega(n)+k + s)) = \frac{1}{N}\sum_{k\in \mathbb{Z}} e(k(\omega(n)+s)) \widehat{f}\bigg(\frac{k}{N}\bigg) \end{equation}
\begin{equation} \sum_{k \in \mathbb{Z}} f(N(\omega(n)+k + s)) = \frac{1}{N}\sum_{k\in \mathbb{Z}} e(k(\omega(n)+s)) \widehat{f}\bigg(\frac{k}{N}\bigg) \end{equation}yielding
 \begin{equation} \mathcal{M}^{(m)}(N) = \frac{1}{N^m} \int_0^1 \sum_{\boldsymbol{\mathbf{n}} \in [N]^m} \sum_{\boldsymbol{\mathbf{k}} \in \mathbb{Z}^m} \widehat{f}\bigg(\frac{\boldsymbol{\mathbf{k}}}{N}\bigg) e(\boldsymbol{\mathbf{k}}\cdot \omega(\boldsymbol{\mathbf{n}}) + \boldsymbol{\mathbf{k}}\cdot \boldsymbol{\mathbf{1}}s)\,{d} s, \end{equation}
\begin{equation} \mathcal{M}^{(m)}(N) = \frac{1}{N^m} \int_0^1 \sum_{\boldsymbol{\mathbf{n}} \in [N]^m} \sum_{\boldsymbol{\mathbf{k}} \in \mathbb{Z}^m} \widehat{f}\bigg(\frac{\boldsymbol{\mathbf{k}}}{N}\bigg) e(\boldsymbol{\mathbf{k}}\cdot \omega(\boldsymbol{\mathbf{n}}) + \boldsymbol{\mathbf{k}}\cdot \boldsymbol{\mathbf{1}}s)\,{d} s, \end{equation}
where ![]() $\omega (\boldsymbol {\mathbf {n}}) := (\omega (n_1), \omega (n_2), \ldots, \omega (n_m))$ and where
$\omega (\boldsymbol {\mathbf {n}}) := (\omega (n_1), \omega (n_2), \ldots, \omega (n_m))$ and where ![]() $\widehat {f}(\frac {\boldsymbol {\mathbf {k}}}{N}) = \prod _{i=1}^m \widehat {f}(\frac {k_i}{N})$.
$\widehat {f}(\frac {\boldsymbol {\mathbf {k}}}{N}) = \prod _{i=1}^m \widehat {f}(\frac {k_i}{N})$.
In [Reference Lutsko and TechnauLT21, § 3] we showed that, if
 \[ \mathcal{E}(N):= \frac{1}{N^m} \int_0^1 \sum_{\boldsymbol{\mathbf{n}} \in [N]^m} \sum_{\substack{\boldsymbol{\mathbf{k}} \in (\mathbb{Z}^{\ast})^m}} \widehat{f}\bigg(\frac{\boldsymbol{\mathbf{k}}}{N}\bigg) e( \boldsymbol{\mathbf{k}}\cdot \omega(\boldsymbol{\mathbf{n}}) + \boldsymbol{\mathbf{k}}\cdot \boldsymbol{\mathbf{1}}s)\,{d} s, \]
\[ \mathcal{E}(N):= \frac{1}{N^m} \int_0^1 \sum_{\boldsymbol{\mathbf{n}} \in [N]^m} \sum_{\substack{\boldsymbol{\mathbf{k}} \in (\mathbb{Z}^{\ast})^m}} \widehat{f}\bigg(\frac{\boldsymbol{\mathbf{k}}}{N}\bigg) e( \boldsymbol{\mathbf{k}}\cdot \omega(\boldsymbol{\mathbf{n}}) + \boldsymbol{\mathbf{k}}\cdot \boldsymbol{\mathbf{1}}s)\,{d} s, \]
then for fixed ![]() $m$, and assuming the inductive hypothesis, Theorem 1.3 reduces to the following lemma.
$m$, and assuming the inductive hypothesis, Theorem 1.3 reduces to the following lemma.
Lemma 3.1 Let ![]() $\mathscr {P}_m$ denote the set of non-isolating partitions of
$\mathscr {P}_m$ denote the set of non-isolating partitions of ![]() $[m]$. We have that
$[m]$. We have that
where the partition ![]() $\mathcal {P} = (P_1, P_2, \ldots, P_d)$, and
$\mathcal {P} = (P_1, P_2, \ldots, P_d)$, and ![]() $|P_i|$ is the size of
$|P_i|$ is the size of ![]() $P_i$.
$P_i$.
3.2 Dyadic decomposition
It is convenient to decompose the sums over ![]() $n$ and
$n$ and ![]() $k$ within
$k$ within ![]() $S_N(s,f)$ into (nearly) dyadic ranges in a smooth manner. Given
$S_N(s,f)$ into (nearly) dyadic ranges in a smooth manner. Given ![]() $N$, we let
$N$, we let ![]() $Q>1$ be the unique integer with
$Q>1$ be the unique integer with ![]() $e^{Q}\leq N < e^{Q+1}$. Now, we describe a smooth partition of unity which approximates the indicator function of
$e^{Q}\leq N < e^{Q+1}$. Now, we describe a smooth partition of unity which approximates the indicator function of ![]() $[1,N]$. Strictly speaking, these partitions depend on
$[1,N]$. Strictly speaking, these partitions depend on ![]() $Q$, but we suppress this from the notation. Furthermore, since we want asymptotics of
$Q$, but we suppress this from the notation. Furthermore, since we want asymptotics of ![]() $\mathcal {E}(N)$, we need to take a bit of care at the right end point of
$\mathcal {E}(N)$, we need to take a bit of care at the right end point of ![]() $[1,N]$, and so a tighter than dyadic decomposition is needed. Let us make this precise, and point out that a detailed construction can be found in the Appendix. For
$[1,N]$, and so a tighter than dyadic decomposition is needed. Let us make this precise, and point out that a detailed construction can be found in the Appendix. For ![]() $0\le q < Q$ we let
$0\le q < Q$ we let ![]() $\mathfrak {N}_q: \mathbb {R}\to [0,1]$ denote a smooth function for which
$\mathfrak {N}_q: \mathbb {R}\to [0,1]$ denote a smooth function for which
and such that ![]() $\mathfrak {N}_{q}(x) + \mathfrak {N}_{q+1}(x) = 1$ for
$\mathfrak {N}_{q}(x) + \mathfrak {N}_{q+1}(x) = 1$ for ![]() $x\in [e^q,e^{q+1})$. Now for
$x\in [e^q,e^{q+1})$. Now for ![]() $q \ge Q$ we let
$q \ge Q$ we let ![]() $\mathfrak {N}_q$ form a smooth partition of unity for which
$\mathfrak {N}_q$ form a smooth partition of unity for which
 \begin{equation} \sum_{q=0}^{2Q-1} \mathfrak{N}_q (x) = \begin{cases} 1 & \mbox{if } 1< x < e^{Q},\\ 0 & \mbox{if } x< 1/2 \mbox{ or } x > N + \dfrac{3N}{\log(N)} \end{cases} \end{equation}
\begin{equation} \sum_{q=0}^{2Q-1} \mathfrak{N}_q (x) = \begin{cases} 1 & \mbox{if } 1< x < e^{Q},\\ 0 & \mbox{if } x< 1/2 \mbox{ or } x > N + \dfrac{3N}{\log(N)} \end{cases} \end{equation}and
while ![]() $\operatorname {supp}(\mathfrak {N}_Q) \subset (0.9\cdot e^{Q-1}, 1.1\cdot e^{Q})$. Let
$\operatorname {supp}(\mathfrak {N}_Q) \subset (0.9\cdot e^{Q-1}, 1.1\cdot e^{Q})$. Let ![]() $\Vert g \Vert _{\infty }$ denote the sup norm of a function
$\Vert g \Vert _{\infty }$ denote the sup norm of a function ![]() $g : \mathbb {R} \to \mathbb {R}$. We impose the following condition on the derivatives:
$g : \mathbb {R} \to \mathbb {R}$. We impose the following condition on the derivatives:
 \begin{equation} \Vert \mathfrak{N}_{q}^{(j)}\Vert_{\infty} \ll \begin{cases} e^{-qj} & \mbox{for } q < Q,\\ (e^{Q}/Q)^{-j} & \mbox{for } Q< q, \end{cases} \end{equation}
\begin{equation} \Vert \mathfrak{N}_{q}^{(j)}\Vert_{\infty} \ll \begin{cases} e^{-qj} & \mbox{for } q < Q,\\ (e^{Q}/Q)^{-j} & \mbox{for } Q< q, \end{cases} \end{equation}
for ![]() $j \ge 1$. For technical reasons, assume
$j \ge 1$. For technical reasons, assume ![]() $\mathfrak {N}_q^{(1)}$ changes sign only once.
$\mathfrak {N}_q^{(1)}$ changes sign only once.
Notice that (3.5) implies
 \[ \sum_{n \in \mathbb{Z}}\sum_{q=0}^{2Q-2} \mathfrak{N}_q (n) \sum_{k \in \mathbb{Z}} f(N(\omega(n) +k +s)) \leq S_N(s,f) \leq\sum_{n\in \mathbb{Z}}\sum_{q=0}^{2Q-1} \mathfrak{N}_q (n) \sum_{k \in \mathbb{Z}} f(N(\omega(n) +k +s)). \]
\[ \sum_{n \in \mathbb{Z}}\sum_{q=0}^{2Q-2} \mathfrak{N}_q (n) \sum_{k \in \mathbb{Z}} f(N(\omega(n) +k +s)) \leq S_N(s,f) \leq\sum_{n\in \mathbb{Z}}\sum_{q=0}^{2Q-1} \mathfrak{N}_q (n) \sum_{k \in \mathbb{Z}} f(N(\omega(n) +k +s)). \]
Ignoring the lower bound, which can be treated similarly, applying Poisson summation for every fixed ![]() $n$ and using the positivity of the inner sum, we then have
$n$ and using the positivity of the inner sum, we then have
 \[ S_N(s,f)\leq \frac{1}{N}\sum_{n \in \mathbb{Z}}\sum_{q=0}^{2Q-1} \mathfrak{N}_q(n) \sum_{k \in \mathbb{Z}} \widehat{f} \bigg(\frac{k}{N}\bigg) e(k(\omega(n) +s)). \]
\[ S_N(s,f)\leq \frac{1}{N}\sum_{n \in \mathbb{Z}}\sum_{q=0}^{2Q-1} \mathfrak{N}_q(n) \sum_{k \in \mathbb{Z}} \widehat{f} \bigg(\frac{k}{N}\bigg) e(k(\omega(n) +s)). \]
Next, by positivity, we have that
 \begin{equation} \mathcal{M}^{(m)}(N) \le \int_0^1 \bigg(\frac{1}{N}\sum_{q=0}^{2Q-1} \sum_{n \in \mathbb{Z}} \mathfrak{N}_{q}(n)\sum_{k \in \mathbb{Z}} \widehat{f}\bigg(\frac{k}{N}\bigg) e( k \omega(n) + ks)\bigg)^m {d} s. \end{equation}
\begin{equation} \mathcal{M}^{(m)}(N) \le \int_0^1 \bigg(\frac{1}{N}\sum_{q=0}^{2Q-1} \sum_{n \in \mathbb{Z}} \mathfrak{N}_{q}(n)\sum_{k \in \mathbb{Z}} \widehat{f}\bigg(\frac{k}{N}\bigg) e( k \omega(n) + ks)\bigg)^m {d} s. \end{equation}
All frequencies ![]() $\boldsymbol {\mathbf {k}}$ for which
$\boldsymbol {\mathbf {k}}$ for which ![]() $k_j=0$ for at least some index
$k_j=0$ for at least some index ![]() $1\leq j\leq m-1$ contribute to
$1\leq j\leq m-1$ contribute to ![]() $\mathcal {M}^{(m)}(N)$ exactly
$\mathcal {M}^{(m)}(N)$ exactly
 \[ \sum_{i=1}^{m-1} \begin{pmatrix} m-1\\ i \end{pmatrix}\widehat{f}(0)^{i}\int_0^1 \bigg(\frac{1}{N}\sum_{n \in [N]}\sum_{k \neq 0} \widehat{f}\bigg(\frac{k}{N}\bigg) e( k \omega(n) + ks)\bigg)^{m-i} {d} s. \]
\[ \sum_{i=1}^{m-1} \begin{pmatrix} m-1\\ i \end{pmatrix}\widehat{f}(0)^{i}\int_0^1 \bigg(\frac{1}{N}\sum_{n \in [N]}\sum_{k \neq 0} \widehat{f}\bigg(\frac{k}{N}\bigg) e( k \omega(n) + ks)\bigg)^{m-i} {d} s. \]
Subtracting exactly the above term from both sides of (3.8), while using our inductive assumption that the ![]() $\mathcal {M}^{m-i}(N)$ converge (for
$\mathcal {M}^{m-i}(N)$ converge (for ![]() $1\leq i\leq m-2)$, then yields
$1\leq i\leq m-2)$, then yields
 \begin{equation} \mathcal{E}(N) \le \int_0^1\bigg(\frac{1}{N}\sum_{q=0}^{2Q-1} \sum_{n \in \mathbb{Z}} \mathfrak{N}_{q}(n)\sum_{k\neq 0}\widehat{f}\bigg(\frac{k}{N}\bigg) e(k \omega(n) + ks)\bigg)^m {d} s +o(1). \end{equation}
\begin{equation} \mathcal{E}(N) \le \int_0^1\bigg(\frac{1}{N}\sum_{q=0}^{2Q-1} \sum_{n \in \mathbb{Z}} \mathfrak{N}_{q}(n)\sum_{k\neq 0}\widehat{f}\bigg(\frac{k}{N}\bigg) e(k \omega(n) + ks)\bigg)^m {d} s +o(1). \end{equation}The same argument can be used to yield
 \[ \mathcal{E}(N)+o(1) \ge \int_0^1\bigg(\frac{1}{N}\sum_{q=0}^{2Q-2} \sum_{n \in \mathbb{Z}} \mathfrak{N}_{q}(n)\sum_{k\neq 0}\widehat{f}\bigg(\frac{k}{N}\bigg) e( k \omega(n) + ks)\bigg)^m {d} s . \]
\[ \mathcal{E}(N)+o(1) \ge \int_0^1\bigg(\frac{1}{N}\sum_{q=0}^{2Q-2} \sum_{n \in \mathbb{Z}} \mathfrak{N}_{q}(n)\sum_{k\neq 0}\widehat{f}\bigg(\frac{k}{N}\bigg) e( k \omega(n) + ks)\bigg)^m {d} s . \]
We similarly decompose the ![]() $k$ sums, although thanks to the compact support of
$k$ sums, although thanks to the compact support of ![]() $\widehat {f}$ we do not need to worry about
$\widehat {f}$ we do not need to worry about ![]() $k\ge N$. Let
$k\ge N$. Let ![]() $\mathfrak {K}_u:\mathbb {R} \to [0,1]$ be a smooth function such that, for
$\mathfrak {K}_u:\mathbb {R} \to [0,1]$ be a smooth function such that, for ![]() $U :=\lceil \log N \rceil$,
$U :=\lceil \log N \rceil$,
 \[ \sum_{u=-U}^{U} \mathfrak{K}_u(k) =\begin{cases} 1 & \mbox{if } \vert k\vert \in [1, N),\\ 0 & \mbox{if } \vert k\vert < 1/2 \mbox{ or } \vert k\vert > 2N, \end{cases} \]
\[ \sum_{u=-U}^{U} \mathfrak{K}_u(k) =\begin{cases} 1 & \mbox{if } \vert k\vert \in [1, N),\\ 0 & \mbox{if } \vert k\vert < 1/2 \mbox{ or } \vert k\vert > 2N, \end{cases} \]
and the symmetry ![]() $\mathfrak {K}_{-u}(k) = \mathfrak {K}_{u}(-k)$ holds true for all
$\mathfrak {K}_{-u}(k) = \mathfrak {K}_{u}(-k)$ holds true for all ![]() $u,k> 0$. Similarly,
$u,k> 0$. Similarly,
 \begin{align*} & \operatorname{supp}(\mathfrak{K}_u) \subset[e^{u }/3, 3e^{u})\quad \mbox{if } u \ge 0,\quad \mbox{and } \\ & \Vert \mathfrak{K}_{u}^{(j)} \Vert_{\infty} \ll e^{-|u|j},\quad \mbox{for all } j\ge 1. \end{align*}
\begin{align*} & \operatorname{supp}(\mathfrak{K}_u) \subset[e^{u }/3, 3e^{u})\quad \mbox{if } u \ge 0,\quad \mbox{and } \\ & \Vert \mathfrak{K}_{u}^{(j)} \Vert_{\infty} \ll e^{-|u|j},\quad \mbox{for all } j\ge 1. \end{align*}
As for ![]() $\mathfrak {N}_q$, we also assume
$\mathfrak {N}_q$, we also assume ![]() $\mathfrak {K}_u^{(1)}$ changes sign exactly once.
$\mathfrak {K}_u^{(1)}$ changes sign exactly once.
Therefore, a central role is played by the smoothed exponential sums
 \begin{equation} \mathcal{E}_{q,u}(s):=\frac{1}{N}\sum_{k\in \mathbb{Z}} \mathfrak{K}_{u}(k) \widehat{f}\bigg(\frac{k}{N}\bigg)e( ks)\sum_{n\in \mathbb{Z}} \mathfrak{N}_{q}(n)e( k\omega(n) ). \end{equation}
\begin{equation} \mathcal{E}_{q,u}(s):=\frac{1}{N}\sum_{k\in \mathbb{Z}} \mathfrak{K}_{u}(k) \widehat{f}\bigg(\frac{k}{N}\bigg)e( ks)\sum_{n\in \mathbb{Z}} \mathfrak{N}_{q}(n)e( k\omega(n) ). \end{equation}
Notice that (3.9) and the compact support of ![]() $\widehat {f}$ imply
$\widehat {f}$ imply
 \[ \mathcal{E}(N) \ll \bigg\Vert \sum_{u=-U}^{U}\sum_{q=0}^{2Q-1} \mathcal{E}_{q,u}\bigg\Vert_{L^m(\mathbb{R})}^m. \]
\[ \mathcal{E}(N) \ll \bigg\Vert \sum_{u=-U}^{U}\sum_{q=0}^{2Q-1} \mathcal{E}_{q,u}\bigg\Vert_{L^m(\mathbb{R})}^m. \]
Now write
 \[ \mathcal{F}(N) := \frac{1}{N^m}\sum_{\boldsymbol{\mathbf{q}}\in [0,2Q-1]^m} \sum_{\boldsymbol{\mathbf{u}} = [-U,U]^m}\sum_{\boldsymbol{\mathbf{k}},\boldsymbol{\mathbf{n}} \in \mathbb{Z}^m} \mathfrak{K}_{\boldsymbol{\mathbf{u}}}(\boldsymbol{\mathbf{k}})\mathfrak{N}_{\boldsymbol{\mathbf{q}}}(\boldsymbol{\mathbf{n}}) \int_0^1\widehat{f}\bigg(\frac{\boldsymbol{\mathbf{k}}}{N}\bigg) e( \boldsymbol{\mathbf{k}}\cdot \omega(\boldsymbol{\mathbf{n}}) + \boldsymbol{\mathbf{k}}\cdot \boldsymbol{\mathbf{1}} s)\, {d} s, \]
\[ \mathcal{F}(N) := \frac{1}{N^m}\sum_{\boldsymbol{\mathbf{q}}\in [0,2Q-1]^m} \sum_{\boldsymbol{\mathbf{u}} = [-U,U]^m}\sum_{\boldsymbol{\mathbf{k}},\boldsymbol{\mathbf{n}} \in \mathbb{Z}^m} \mathfrak{K}_{\boldsymbol{\mathbf{u}}}(\boldsymbol{\mathbf{k}})\mathfrak{N}_{\boldsymbol{\mathbf{q}}}(\boldsymbol{\mathbf{n}}) \int_0^1\widehat{f}\bigg(\frac{\boldsymbol{\mathbf{k}}}{N}\bigg) e( \boldsymbol{\mathbf{k}}\cdot \omega(\boldsymbol{\mathbf{n}}) + \boldsymbol{\mathbf{k}}\cdot \boldsymbol{\mathbf{1}} s)\, {d} s, \]
where ![]() $\mathfrak {N}_{\boldsymbol {\mathbf {q}}}(\boldsymbol {\mathbf {n}}) := \mathfrak {N}_{q_1}(n_1)\mathfrak {N}_{q_2}(n_2)\cdots \mathfrak {N}_{q_m}(n_m)$ and
$\mathfrak {N}_{\boldsymbol {\mathbf {q}}}(\boldsymbol {\mathbf {n}}) := \mathfrak {N}_{q_1}(n_1)\mathfrak {N}_{q_2}(n_2)\cdots \mathfrak {N}_{q_m}(n_m)$ and ![]() $\mathfrak {K}_{\boldsymbol {\mathbf {u}}}(\boldsymbol {\mathbf {k}}) := \mathfrak {K}_{u_1}(k_1)\mathfrak {K}_{u_2}(k_2)\cdots \mathfrak {K}_{u_m}(k_m)$. Our goal will be to establish that
$\mathfrak {K}_{\boldsymbol {\mathbf {u}}}(\boldsymbol {\mathbf {k}}) := \mathfrak {K}_{u_1}(k_1)\mathfrak {K}_{u_2}(k_2)\cdots \mathfrak {K}_{u_m}(k_m)$. Our goal will be to establish that ![]() $\mathcal {F}(N)$ is equal to the right-hand side of (3.4) up to an
$\mathcal {F}(N)$ is equal to the right-hand side of (3.4) up to an ![]() $o(1)$ term. Then, since we can establish the same asymptotic for the lower bound, we may conclude the asymptotic for
$o(1)$ term. Then, since we can establish the same asymptotic for the lower bound, we may conclude the asymptotic for ![]() $\mathcal {E}(N)$. Since the details are identical, we will only focus on
$\mathcal {E}(N)$. Since the details are identical, we will only focus on ![]() $\mathcal {F}(N)$.
$\mathcal {F}(N)$.
Fixing ![]() $\boldsymbol {\mathbf {q}}$ and
$\boldsymbol {\mathbf {q}}$ and ![]() $\boldsymbol {\mathbf {u}}$, we let
$\boldsymbol {\mathbf {u}}$, we let
 \[ \mathcal{F}_{\boldsymbol{\mathbf{q}},\boldsymbol{\mathbf{u}}}(N)=\frac{1}{N^m}\int_0^1\sum_{\substack{\boldsymbol{\mathbf{n}},\boldsymbol{\mathbf{k}} \in \mathbb{Z}^m}} \mathfrak{N}_{\boldsymbol{\mathbf{q}}}(\boldsymbol{\mathbf{n}})\mathfrak{K}_{\boldsymbol{\mathbf{u}}}(\boldsymbol{\mathbf{k}}) \widehat{f}\bigg(\frac{\boldsymbol{\mathbf{k}}}{N}\bigg) e(\boldsymbol{\mathbf{k}}\cdot \omega(\boldsymbol{\mathbf{n}}) + \boldsymbol{\mathbf{k}}\cdot \boldsymbol{\mathbf{1}}s) \,{d} s. \]
\[ \mathcal{F}_{\boldsymbol{\mathbf{q}},\boldsymbol{\mathbf{u}}}(N)=\frac{1}{N^m}\int_0^1\sum_{\substack{\boldsymbol{\mathbf{n}},\boldsymbol{\mathbf{k}} \in \mathbb{Z}^m}} \mathfrak{N}_{\boldsymbol{\mathbf{q}}}(\boldsymbol{\mathbf{n}})\mathfrak{K}_{\boldsymbol{\mathbf{u}}}(\boldsymbol{\mathbf{k}}) \widehat{f}\bigg(\frac{\boldsymbol{\mathbf{k}}}{N}\bigg) e(\boldsymbol{\mathbf{k}}\cdot \omega(\boldsymbol{\mathbf{n}}) + \boldsymbol{\mathbf{k}}\cdot \boldsymbol{\mathbf{1}}s) \,{d} s. \]
Remark In the following sections, we will fix ![]() $\boldsymbol {\mathbf {q}}$ and
$\boldsymbol {\mathbf {q}}$ and ![]() $\boldsymbol {\mathbf {u}}$. Because of the way we have defined
$\boldsymbol {\mathbf {u}}$. Because of the way we have defined ![]() $\mathfrak {N}_q$, this implies two cases:
$\mathfrak {N}_q$, this implies two cases: ![]() $q< Q$ and
$q< Q$ and ![]() $q\ge Q$. The only real difference in these two cases are the bounds in (3.7), which differ by a factor of
$q\ge Q$. The only real difference in these two cases are the bounds in (3.7), which differ by a factor of ![]() $Q = \log (N)$. To keep the notation simple, we will assume we have
$Q = \log (N)$. To keep the notation simple, we will assume we have ![]() $q < Q$ and work with the first bound. In practice the logarithmic correction does not affect any of the results or proofs.
$q < Q$ and work with the first bound. In practice the logarithmic correction does not affect any of the results or proofs.
4. Applying the  $B$-process
$B$-process
4.1 Degenerate regimes
Fix ![]() $\delta = {1/(m + 1)}$. We say that
$\delta = {1/(m + 1)}$. We say that ![]() $(q,u)\in [2 Q] \times [-U,U]$ is degenerate if either
$(q,u)\in [2 Q] \times [-U,U]$ is degenerate if either
holds. Otherwise ![]() $(q,u)$ is called non-degenerate. Let
$(q,u)$ is called non-degenerate. Let ![]() $\mathscr {G}(N)$ denote the set of all non-degenerate pairs
$\mathscr {G}(N)$ denote the set of all non-degenerate pairs ![]() $(q,u)$. In this section it is enough to suppose that
$(q,u)$. In this section it is enough to suppose that ![]() $u>0$ (and therefore
$u>0$ (and therefore ![]() $k>0$). Next, we show that degenerate
$k>0$). Next, we show that degenerate ![]() $(q,u)$ contribute a negligible amount to
$(q,u)$ contribute a negligible amount to ![]() $\mathcal {F}(N)$.
$\mathcal {F}(N)$.
First, assume ![]() $q \le \delta Q$. Expanding the
$q \le \delta Q$. Expanding the ![]() $m$th power, evaluating the
$m$th power, evaluating the ![]() $s$-integral and trivial estimation yield
$s$-integral and trivial estimation yield
 \begin{align*} \Vert \mathcal{E}_{q,u} \Vert_{L^m}^m &= \int_0^1\bigg(\frac{1}{N} \sum_{k \in \mathbb{Z}} \mathfrak{K}_u(k)\widehat{f}\bigg(\frac{k}{N}\bigg) e(ks) \sum_{n \in \mathbb{Z}} \mathfrak{N}_{q}(n)e(k\omega(n))\bigg)^m {d}s\\ &\ll \frac{1}{N^m}\sum_{\substack{k_i \asymp e^u,\\ i =1,\ldots m}} \max_x\bigg(\widehat{f}\bigg(\frac{x}{N}\bigg)\bigg)^m\sum_{\substack{n_i \asymp e^q,\\ i =1,\ldots m}} \bigg|\int_0^1 e((k_1+ \cdots + k_m)s)\,{d}s\bigg|\\ &\ll \frac{1}{N^m} \#\{k_1,\ldots,k_m\asymp e^{u}: k_1 +\cdots +k_m = 0 \}N^{m\delta}\ll N^{m\delta-1}. \end{align*}
\begin{align*} \Vert \mathcal{E}_{q,u} \Vert_{L^m}^m &= \int_0^1\bigg(\frac{1}{N} \sum_{k \in \mathbb{Z}} \mathfrak{K}_u(k)\widehat{f}\bigg(\frac{k}{N}\bigg) e(ks) \sum_{n \in \mathbb{Z}} \mathfrak{N}_{q}(n)e(k\omega(n))\bigg)^m {d}s\\ &\ll \frac{1}{N^m}\sum_{\substack{k_i \asymp e^u,\\ i =1,\ldots m}} \max_x\bigg(\widehat{f}\bigg(\frac{x}{N}\bigg)\bigg)^m\sum_{\substack{n_i \asymp e^q,\\ i =1,\ldots m}} \bigg|\int_0^1 e((k_1+ \cdots + k_m)s)\,{d}s\bigg|\\ &\ll \frac{1}{N^m} \#\{k_1,\ldots,k_m\asymp e^{u}: k_1 +\cdots +k_m = 0 \}N^{m\delta}\ll N^{m\delta-1}. \end{align*}
If ![]() $u< q^{(A-1)/2}$ and
$u< q^{(A-1)/2}$ and ![]() $q>\delta Q$, then we can apply the Euler summation formula, followed by van der Corput's lemma with
$q>\delta Q$, then we can apply the Euler summation formula, followed by van der Corput's lemma with ![]() $j=1$, to conclude that
$j=1$, to conclude that
where the numerator is the size of the support of ![]() $\mathfrak {N}_q$ and the denominator is the maximum value of
$\mathfrak {N}_q$ and the denominator is the maximum value of ![]() $k \omega '(x)$ for
$k \omega '(x)$ for ![]() $x$ in that support. Hence,
$x$ in that support. Hence,
Note
 \[ \sum_{q\leq Q}\frac{e^{q}}{q^{A-1}}\ll\int_{1}^{Q}\frac{e^{q}}{q^{A-1}}{d}q= \int_{1}^{Q/2}\frac{e^{q}}{q^{A-1}}{d}q+\int_{Q/2}^{Q} \frac{e^{q}}{q^{A-1}}{d}q\ll e^{Q/2}+\frac{1}{Q^{A-1}} \int_{Q/2}^{Q}e^{Q}\,{d}q\ll\frac{e^{Q}}{Q^{A-1}}. \]
\[ \sum_{q\leq Q}\frac{e^{q}}{q^{A-1}}\ll\int_{1}^{Q}\frac{e^{q}}{q^{A-1}}{d}q= \int_{1}^{Q/2}\frac{e^{q}}{q^{A-1}}{d}q+\int_{Q/2}^{Q} \frac{e^{q}}{q^{A-1}}{d}q\ll e^{Q/2}+\frac{1}{Q^{A-1}} \int_{Q/2}^{Q}e^{Q}\,{d}q\ll\frac{e^{Q}}{Q^{A-1}}. \]
Thus,
 \[ \bigg\Vert \sum_{\delta Q\leq q\leq Q} \sum_{u\leq q^{(A-1)/2}} \mathcal{E}_{q,u}\bigg\Vert_\infty \ll\frac{1}{N} \sum_{q\leq Q} \sum_{u\leq q^{(A-1)/2}}\sum_{k\asymp e^{u}}\frac{1}{k} \frac{e^{q}}{q^{A-1}}\ll\frac{1}{N} \frac{e^{Q}}{Q^{A-1}} \sum_{u\leq Q^{(A-1)/2}}1\leq\frac{1}{Q^{{(A-1)/2}}}. \]
\[ \bigg\Vert \sum_{\delta Q\leq q\leq Q} \sum_{u\leq q^{(A-1)/2}} \mathcal{E}_{q,u}\bigg\Vert_\infty \ll\frac{1}{N} \sum_{q\leq Q} \sum_{u\leq q^{(A-1)/2}}\sum_{k\asymp e^{u}}\frac{1}{k} \frac{e^{q}}{q^{A-1}}\ll\frac{1}{N} \frac{e^{Q}}{Q^{A-1}} \sum_{u\leq Q^{(A-1)/2}}1\leq\frac{1}{Q^{{(A-1)/2}}}. \]
Taking the ![]() $L^m$-norm then yields
$L^m$-norm then yields
 \[ \bigg\Vert \sum_{(q,u)\in [2Q]\times[-U,U] \setminus \mathscr{G}(N)}\mathcal{E}_{q,u}\bigg\Vert_{L^m}^m \ll_{\delta} \log(N)^{-\rho}, \]
\[ \bigg\Vert \sum_{(q,u)\in [2Q]\times[-U,U] \setminus \mathscr{G}(N)}\mathcal{E}_{q,u}\bigg\Vert_{L^m}^m \ll_{\delta} \log(N)^{-\rho}, \]
for some ![]() $\rho >0$. Hence, the triangle inequality implies
$\rho >0$. Hence, the triangle inequality implies
 \begin{equation} \mathcal{F}(N) =\bigg\Vert \sum_{(u,q) \in \mathscr{G}(N)}\mathcal{E}_{q,u} \bigg\Vert_{L^m}^m + O(N^{-\rho}). \end{equation}
\begin{equation} \mathcal{F}(N) =\bigg\Vert \sum_{(u,q) \in \mathscr{G}(N)}\mathcal{E}_{q,u} \bigg\Vert_{L^m}^m + O(N^{-\rho}). \end{equation} Next, to dismiss the degenerate regimes, let ![]() $w,W$ denote strictly positive numbers satisfying
$w,W$ denote strictly positive numbers satisfying ![]() $w< W$. Consider
$w< W$. Consider
where ![]() $\| \cdot \|$ denotes the distance to the nearest integer. We shall need (as in [Reference Lutsko and TechnauLT21, Proof of Lemma 4.1]) the following lemma.
$\| \cdot \|$ denotes the distance to the nearest integer. We shall need (as in [Reference Lutsko and TechnauLT21, Proof of Lemma 4.1]) the following lemma.
Lemma 4.1 If ![]() $W<1/10$, then
$W<1/10$, then
 \[ \sum_{e^{u}\leq |k|< e^{u+1}}g_{w,W}(k)\ll\bigg(e^{u}+\frac{1}{w}\bigg)\log(1/W) \]
\[ \sum_{e^{u}\leq |k|< e^{u+1}}g_{w,W}(k)\ll\bigg(e^{u}+\frac{1}{w}\bigg)\log(1/W) \]
where the implied constant is absolute.
Proof. The proof is elementary, hence we only sketch the main idea. If ![]() $e^{u}w <1$ then we achieve the bound
$e^{u}w <1$ then we achieve the bound ![]() $(1/w) \log (1/W)$, and otherwise we get the bound
$(1/w) \log (1/W)$, and otherwise we get the bound ![]() $e^{u}\log (1/W)$. Focusing on the latter, first make a case distinction between those
$e^{u}\log (1/W)$. Focusing on the latter, first make a case distinction between those ![]() $x$ which contribute
$x$ which contribute ![]() $\frac {1}{\|xw\|}$ and those that contribute
$\frac {1}{\|xw\|}$ and those that contribute ![]() $\frac {1}{W}$. Then count how many contribute the latter. For the former, since the spacing between consecutive points is small, we can convert the sum into
$\frac {1}{W}$. Then count how many contribute the latter. For the former, since the spacing between consecutive points is small, we can convert the sum into ![]() $e^uw$ many integrals of the form
$e^uw$ many integrals of the form ![]() $(1/w) \int _{W/w}^{1/w} (1/x) \,{d}x$.
$(1/w) \int _{W/w}^{1/w} (1/x) \,{d}x$.
With the previous lemma at hand, we can show that an additional degenerate regime is negligible. Specifically, when we apply the ![]() $B$-process, the first step is to apply Poisson summation. Depending on the new summation variable there may, or may not, be a stationary point. The following lemma allows us to dismiss the contribution when there is no stationary point. Fix
$B$-process, the first step is to apply Poisson summation. Depending on the new summation variable there may, or may not, be a stationary point. The following lemma allows us to dismiss the contribution when there is no stationary point. Fix ![]() $k\asymp e^{u}$ and let
$k\asymp e^{u}$ and let ![]() $[a,b]:=\mathrm {supp}(\mathfrak {N}_{q})$. Consider
$[a,b]:=\mathrm {supp}(\mathfrak {N}_{q})$. Consider
 \[ \mathrm{Err}(k):=\sum_{\underset{m_{q}(r)>0}{r\in\mathbb{Z}}} \int_{\mathbb{R}} e(\Phi_r(x)) \mathfrak{N}_{q}(x)\,{d}x, \]
\[ \mathrm{Err}(k):=\sum_{\underset{m_{q}(r)>0}{r\in\mathbb{Z}}} \int_{\mathbb{R}} e(\Phi_r(x)) \mathfrak{N}_{q}(x)\,{d}x, \]
where
Our next aim is to show that the smooth exponential sum
 \[ \mathrm{Err}_{u}(s):=\sum_{k\in\mathbb{Z}}e(ks)\mathrm{Err}(k)\mathfrak{K}_{u}(k) \widehat{f}\bigg(\frac{k}{N}\bigg) \]
\[ \mathrm{Err}_{u}(s):=\sum_{k\in\mathbb{Z}}e(ks)\mathrm{Err}(k)\mathfrak{K}_{u}(k) \widehat{f}\bigg(\frac{k}{N}\bigg) \]
is small on average over ![]() $s$.
$s$.
Lemma 4.2 Fix any constant ![]() $C>0$. Then the bound
$C>0$. Then the bound
 \begin{equation} I_{\boldsymbol{\mathbf{u}}}:=\int_0^1\prod_{i=1}^m \operatorname{Err}_{u_i}(s)\,{d}s\ll Q^{-C}N^{m} \end{equation}
\begin{equation} I_{\boldsymbol{\mathbf{u}}}:=\int_0^1\prod_{i=1}^m \operatorname{Err}_{u_i}(s)\,{d}s\ll Q^{-C}N^{m} \end{equation}
holds uniformly in ![]() $Q^{{(A-1)/2}}\leq \boldsymbol {\mathbf {u}}\ll Q$.
$Q^{{(A-1)/2}}\leq \boldsymbol {\mathbf {u}}\ll Q$.
Proof. Let ![]() $\mathcal {L}_{\boldsymbol {\mathbf {u}}}$ denote the truncated sub-lattice of
$\mathcal {L}_{\boldsymbol {\mathbf {u}}}$ denote the truncated sub-lattice of ![]() $\mathbb {Z}^{m}$ defined by gathering all
$\mathbb {Z}^{m}$ defined by gathering all ![]() $\boldsymbol {\mathbf {k}}\in \mathbb {Z}^{m}$ so that
$\boldsymbol {\mathbf {k}}\in \mathbb {Z}^{m}$ so that ![]() $k_{1}+\cdots +k_{m}=0$ and
$k_{1}+\cdots +k_{m}=0$ and ![]() $\vert k_{i}\vert \asymp e^{u_i}$ for all
$\vert k_{i}\vert \asymp e^{u_i}$ for all ![]() $i\leq m$. The quantity
$i\leq m$. The quantity ![]() $\mathcal {L}_{\boldsymbol {\mathbf {u}}}$ arises from
$\mathcal {L}_{\boldsymbol {\mathbf {u}}}$ arises from
 \begin{equation} I_{\boldsymbol{\mathbf{u}}}=\sum_{\underset{i\leq m}{|k_{i}|\asymp e^{u}}}\bigg(\bigg(\prod_{i\leq m} \mathrm{Err}(k_{i})\mathfrak{K}_{u}(k_{i})\widehat{f}\bigg(\frac{k_i}{N}\bigg)\bigg) \int_{0}^{1}e((k_{1}+\cdots+k_{m})s)\,{d}s\bigg)\ll \sum_{\boldsymbol{\mathbf{k}}\in\mathcal{L}_{\boldsymbol{\mathbf{u}}}} \bigg(\prod_{i\leq m}\mathrm{Err}(k_{i})\bigg).\end{equation}
\begin{equation} I_{\boldsymbol{\mathbf{u}}}=\sum_{\underset{i\leq m}{|k_{i}|\asymp e^{u}}}\bigg(\bigg(\prod_{i\leq m} \mathrm{Err}(k_{i})\mathfrak{K}_{u}(k_{i})\widehat{f}\bigg(\frac{k_i}{N}\bigg)\bigg) \int_{0}^{1}e((k_{1}+\cdots+k_{m})s)\,{d}s\bigg)\ll \sum_{\boldsymbol{\mathbf{k}}\in\mathcal{L}_{\boldsymbol{\mathbf{u}}}} \bigg(\prod_{i\leq m}\mathrm{Err}(k_{i})\bigg).\end{equation}
Partial integration and the dyadic decomposition allow one to show that the contribution of ![]() $\vert r\vert \geq Q^{O(1)}$ to
$\vert r\vert \geq Q^{O(1)}$ to ![]() $\operatorname {Err}(k_i)$ can be bounded by
$\operatorname {Err}(k_i)$ can be bounded by ![]() $O(Q^{-C})$ for any
$O(Q^{-C})$ for any ![]() $C>0$. Hence, from van der Corput's lemma (Lemma 2.3) with
$C>0$. Hence, from van der Corput's lemma (Lemma 2.3) with ![]() $j=2$ and the assumption
$j=2$ and the assumption ![]() $m_{q}(r)>0$, we infer
$m_{q}(r)>0$, we infer
where the implied constant is absolute. Notice that ![]() $\omega '(a)\asymp q^{A-1}e^{-q}=:w$ and
$\omega '(a)\asymp q^{A-1}e^{-q}=:w$ and
Thus, ![]() $\mathrm {Err}(k)\ll g_{w,W}(k) Q^{O(1)}.$ Using
$\mathrm {Err}(k)\ll g_{w,W}(k) Q^{O(1)}.$ Using ![]() $\mathrm {Err}(k_{i})\ll g_{w,W}(k_{i}) Q^{O(1)}$ for
$\mathrm {Err}(k_{i})\ll g_{w,W}(k_{i}) Q^{O(1)}$ for ![]() $i< m$ and
$i< m$ and ![]() $\mathrm {Err}(k_{m})\ll Q^{O(1)}/W$ in (4.3) produces the estimate
$\mathrm {Err}(k_{m})\ll Q^{O(1)}/W$ in (4.3) produces the estimate
 \begin{equation} I_{\boldsymbol{\mathbf{u}}}\ll\frac{Q^{O(1)}}{W}\sum_{\underset{i< m}{\vert k_{i}\vert\asymp e^{u}}} \bigg(\prod_{i< m}g_{w,W}(k_{i})\bigg)=\frac{Q^{O(1)}}{W} \bigg(\sum_{\vert k \vert \asymp e^{u}}g_{w,W}(k)\bigg)^{m-1}.\end{equation}
\begin{equation} I_{\boldsymbol{\mathbf{u}}}\ll\frac{Q^{O(1)}}{W}\sum_{\underset{i< m}{\vert k_{i}\vert\asymp e^{u}}} \bigg(\prod_{i< m}g_{w,W}(k_{i})\bigg)=\frac{Q^{O(1)}}{W} \bigg(\sum_{\vert k \vert \asymp e^{u}}g_{w,W}(k)\bigg)^{m-1}.\end{equation}
Suppose ![]() $W\geq N^{-\varepsilon }$. Then
$W\geq N^{-\varepsilon }$. Then ![]() $g_{w,W}(k)\leq N^{\varepsilon }$ and we obtain that
$g_{w,W}(k)\leq N^{\varepsilon }$ and we obtain that
Now suppose ![]() $W< N^{-\varepsilon }\leq 1/10$. Then Lemma 4.1 is applicable and yields
$W< N^{-\varepsilon }\leq 1/10$. Then Lemma 4.1 is applicable and yields
Plugging this into (4.4) and using ![]() $1/W\ll e^{q-u/2}q^{(1-A)/2}\ll Ne^{-\frac {u}{2}}$ shows that
$1/W\ll e^{q-u/2}q^{(1-A)/2}\ll Ne^{-\frac {u}{2}}$ shows that
Because ![]() $u\geq Q^{{(A-1)/2}}$, we certainly have
$u\geq Q^{{(A-1)/2}}$, we certainly have ![]() $e^{-\frac {u}{2}}\ll Q^{-C}$ for any
$e^{-\frac {u}{2}}\ll Q^{-C}$ for any ![]() $C>0$ and thus the proof is complete.
$C>0$ and thus the proof is complete.
4.2 First application of the  $B$-process
$B$-process
First, following the lead set out in [Reference Lutsko, Sourmelidis and TechnauLST24], we apply the ![]() $B$-process in the
$B$-process in the ![]() $n$-variable. Assume without loss of generality that
$n$-variable. Assume without loss of generality that ![]() $k >0$ (if
$k >0$ (if ![]() $k <0$ we take complex conjugates and the without loss of generality assumption that
$k <0$ we take complex conjugates and the without loss of generality assumption that ![]() $f$ is even).
$f$ is even).
Then, after applying the ![]() $B$-process, the phase function
$B$-process, the phase function ![]() $x\mapsto k\omega (x) - rx$ will be transformed to
$x\mapsto k\omega (x) - rx$ will be transformed to
 \[ \phi(k,r): = k\omega(x_{k,r}) - r x_{k,r}\quad \mathrm{where}\ x_{k,r} := \begin{cases} \widetilde{\omega}\bigg(\dfrac{r}{k}\bigg) & \text{if } \dfrac{r}{k}>e^{A-1},\\ 3 & \text{otherwise,} \end{cases} \]
\[ \phi(k,r): = k\omega(x_{k,r}) - r x_{k,r}\quad \mathrm{where}\ x_{k,r} := \begin{cases} \widetilde{\omega}\bigg(\dfrac{r}{k}\bigg) & \text{if } \dfrac{r}{k}>e^{A-1},\\ 3 & \text{otherwise,} \end{cases} \]
and ![]() $\widetilde {\omega }(x):= (\omega ^{\prime })^{-1}(x)$ is the inverse of the derivative of
$\widetilde {\omega }(x):= (\omega ^{\prime })^{-1}(x)$ is the inverse of the derivative of ![]() $\omega$. Importantly, the next proposition states that
$\omega$. Importantly, the next proposition states that ![]() $\mathcal {E}_{q,u}$ is well approximated by
$\mathcal {E}_{q,u}$ is well approximated by
 \begin{equation} \mathcal{E}_{q,u}^{(B)}(s):=\frac{e(-1/8)}{N}\sum_{k > 0} \mathfrak{K}_{ u}(k)\widehat{f} \bigg(\frac{ k}{N}\bigg) e(ks)\sum_{r\geq 0} \frac{\mathfrak{N}_{q}(x_{k,r})}{\sqrt{|k\omega^{\prime\prime}(x_{k,r})|}}e(\phi(k,r)). \end{equation}
\begin{equation} \mathcal{E}_{q,u}^{(B)}(s):=\frac{e(-1/8)}{N}\sum_{k > 0} \mathfrak{K}_{ u}(k)\widehat{f} \bigg(\frac{ k}{N}\bigg) e(ks)\sum_{r\geq 0} \frac{\mathfrak{N}_{q}(x_{k,r})}{\sqrt{|k\omega^{\prime\prime}(x_{k,r})|}}e(\phi(k,r)). \end{equation}
We comment on the definition of ![]() $x_{k,r}$ and
$x_{k,r}$ and ![]() $\mathcal {E}_{q,u}^{(B)}$ in the next remark.
$\mathcal {E}_{q,u}^{(B)}$ in the next remark.
Remark Recall that we currently work in the non-degenerate regime, ![]() $q\geq \delta Q$. Note that
$q\geq \delta Q$. Note that ![]() $x_{k,r}$ is the stationary point for the map
$x_{k,r}$ is the stationary point for the map ![]() $x \mapsto k \omega (x)-rx$ when
$x \mapsto k \omega (x)-rx$ when ![]() $r/k > e^{A-1}$ (i.e. when there is a unique stationary point in the relevant regime). On the other hand,
$r/k > e^{A-1}$ (i.e. when there is a unique stationary point in the relevant regime). On the other hand, ![]() $\mathfrak {N}_q(3)=0$ since
$\mathfrak {N}_q(3)=0$ since ![]() $\inf (\operatorname {supp}(\mathfrak {N}_q)) \rightarrow \infty$ as
$\inf (\operatorname {supp}(\mathfrak {N}_q)) \rightarrow \infty$ as ![]() $Q\rightarrow \infty$. Thus,
$Q\rightarrow \infty$. Thus, ![]() $\mathfrak {N}_q(x_{k,r})$ is well defined and smooth as a function of
$\mathfrak {N}_q(x_{k,r})$ is well defined and smooth as a function of ![]() $k,r\geq 0$.
$k,r\geq 0$.
Proposition 4.3 If ![]() $u\geq Q^{(A-1)/2}$, then
$u\geq Q^{(A-1)/2}$, then
uniformly for all non-degenerate ![]() $(u,q)\in \mathscr {G}(N)$.
$(u,q)\in \mathscr {G}(N)$.
Proof. Let ![]() $[a,b]:= \operatorname {supp}(\mathfrak {N}_q)$, let
$[a,b]:= \operatorname {supp}(\mathfrak {N}_q)$, let ![]() $\Phi _r(x):= k\omega (x) - rx$, and let
$\Phi _r(x):= k\omega (x) - rx$, and let ![]() $m(r):= \min \{|\Phi _r^\prime (x)|:\ x \in [a,b]\}$. As usual when applying the
$m(r):= \min \{|\Phi _r^\prime (x)|:\ x \in [a,b]\}$. As usual when applying the ![]() $B$-process we first apply Poisson summation and integration by parts:
$B$-process we first apply Poisson summation and integration by parts:
 \[ \sum_{n \in \mathbb{Z}} \mathfrak{N}_q(n) e(k\omega(n)) = \sum_{r \in \mathbb{Z}} \int_{-\infty}^\infty \mathfrak{N}_q(x) e(\Phi_r(x)) \,{d}x = M(k) + \operatorname{Err}(k), \]
\[ \sum_{n \in \mathbb{Z}} \mathfrak{N}_q(n) e(k\omega(n)) = \sum_{r \in \mathbb{Z}} \int_{-\infty}^\infty \mathfrak{N}_q(x) e(\Phi_r(x)) \,{d}x = M(k) + \operatorname{Err}(k), \]
where ![]() $M(k)$ gathers the contributions when
$M(k)$ gathers the contributions when ![]() $r\in \mathbb {Z}$ with
$r\in \mathbb {Z}$ with ![]() $m(r)=0$ (i.e. with a stationary point) and
$m(r)=0$ (i.e. with a stationary point) and ![]() $\operatorname {Err}(k)$ gathers the contribution of
$\operatorname {Err}(k)$ gathers the contribution of ![]() $0 < m(r)$.
$0 < m(r)$.
In the notation of Lemma 2.2, let ![]() $w(x):= \mathfrak {N}_q(x)$,
$w(x):= \mathfrak {N}_q(x)$, ![]() $\Lambda _{\psi } := \omega (e^q)e^{u} = q^{A}e^{u}$, and
$\Lambda _{\psi } := \omega (e^q)e^{u} = q^{A}e^{u}$, and ![]() $\Omega _\psi = \Omega _{w} := e^q$. Since
$\Omega _\psi = \Omega _{w} := e^q$. Since ![]() $(u,q)$ is non-degenerate we have that
$(u,q)$ is non-degenerate we have that ![]() $\Lambda _\psi /\Omega _\psi \gg q$, and hence
$\Lambda _\psi /\Omega _\psi \gg q$, and hence
 \begin{equation} M(k) = e(-1/8)\sum_{r\geq 0} \frac{\mathfrak{N}_{q}(x_{k,r})}{\sqrt{|k\omega^{\prime\prime}(x_{k,r})|}} e(\phi(k,r)) + O((q \Lambda_\psi^{1/2+O(\varepsilon)})^{-1}). \end{equation}
\begin{equation} M(k) = e(-1/8)\sum_{r\geq 0} \frac{\mathfrak{N}_{q}(x_{k,r})}{\sqrt{|k\omega^{\prime\prime}(x_{k,r})|}} e(\phi(k,r)) + O((q \Lambda_\psi^{1/2+O(\varepsilon)})^{-1}). \end{equation}
Summing (4.7) against ![]() $N^{-1} \mathfrak {K}_{u}(k) \widehat {f}( k/N) e(ks)$ for
$N^{-1} \mathfrak {K}_{u}(k) \widehat {f}( k/N) e(ks)$ for ![]() $k\geq 0$ gives rise to
$k\geq 0$ gives rise to ![]() $\mathcal {E}_{q,u}^{\mathrm {(B)}}$. The term coming from
$\mathcal {E}_{q,u}^{\mathrm {(B)}}$. The term coming from
can be bounded sufficiently by Lemma 4.2 and the triangle inequality.
Since ![]() $x_{k,r}$ is roughly of size
$x_{k,r}$ is roughly of size ![]() $e^{q}$, if we stop here and apply the triangle inequality to (4.5) we would get
$e^{q}$, if we stop here and apply the triangle inequality to (4.5) we would get
 \begin{align*} |\mathcal{E}_{q,u}^{(B)}(s)|\ll\frac{1}{N}\sum_{k > 0} \mathfrak{K}_{u}(k) e^q \frac{1}{\sqrt{k}} \frac{k}{e^q} \ll\frac{1}{N} e^{3u/2} \ll N^{1/2}. \end{align*}
\begin{align*} |\mathcal{E}_{q,u}^{(B)}(s)|\ll\frac{1}{N}\sum_{k > 0} \mathfrak{K}_{u}(k) e^q \frac{1}{\sqrt{k}} \frac{k}{e^q} \ll\frac{1}{N} e^{3u/2} \ll N^{1/2}. \end{align*}
Hence, we still need to find a saving of ![]() $O(N^{1/2})$. To achieve most of this, we now apply the
$O(N^{1/2})$. To achieve most of this, we now apply the ![]() $B$-process in the
$B$-process in the ![]() $k$ variable. This will require the following a priori bounds.
$k$ variable. This will require the following a priori bounds.
4.3 Amplitude bounds
Before proceeding with the second application of the ![]() $B$-process, we require bounds on the amplitude function
$B$-process, we require bounds on the amplitude function
and its derivatives; for which we have the following lemma.
Lemma 4.4 For any pair ![]() $q,u$ as above, and any
$q,u$ as above, and any ![]() $j \ge 1$, we have the bounds
$j \ge 1$, we have the bounds
where the implicit constant in the exponent depends on ![]() $j$, but not
$j$, but not ![]() $q,u$. Moreover,
$q,u$. Moreover,
Proof. First, note that since ![]() $\Psi _{q,u}$ is a product of functions of
$\Psi _{q,u}$ is a product of functions of ![]() $k$, if we can establish (4.8) for each of these functions, then the overall bound will hold for
$k$, if we can establish (4.8) for each of these functions, then the overall bound will hold for ![]() $\Psi _{q,u}(k,r,s)$ by the product rule. Moreover, the bound is obvious for
$\Psi _{q,u}(k,r,s)$ by the product rule. Moreover, the bound is obvious for ![]() $\mathfrak {K}_u(k)$,
$\mathfrak {K}_u(k)$, ![]() $\widehat {f}(k/N)$, and
$\widehat {f}(k/N)$, and ![]() $k^{-1/2}$.
$k^{-1/2}$.
Thus, consider first ![]() $\partial _k \mathfrak {N}_q(x_{k,r}) = \mathfrak {N}_q^\prime (x_{k,r}) \partial _k(x_{k,r})$. By assumption, since
$\partial _k \mathfrak {N}_q(x_{k,r}) = \mathfrak {N}_q^\prime (x_{k,r}) \partial _k(x_{k,r})$. By assumption, since ![]() $x_{k,r} \asymp e^{q}$, we have that
$x_{k,r} \asymp e^{q}$, we have that ![]() $\mathfrak {N}_q^\prime (x_{k,r}) \ll e^{-q}$. Again, by repeated application of the product rule, it suffices to show that
$\mathfrak {N}_q^\prime (x_{k,r}) \ll e^{-q}$. Again, by repeated application of the product rule, it suffices to show that ![]() $\partial _k^j x_{k,r} \ll e^{q-uj}Q^{O(1)}$. To that end, begin with the equation
$\partial _k^j x_{k,r} \ll e^{q-uj}Q^{O(1)}$. To that end, begin with the equation
Hence, ![]() $\widetilde {\omega }^\prime (\omega ^\prime (x)) = \frac {1}{\omega ^{\prime \prime }(x)}$ which we can write as
$\widetilde {\omega }^\prime (\omega ^\prime (x)) = \frac {1}{\omega ^{\prime \prime }(x)}$ which we can write as
where ![]() $f_1$ is a rational function. Now we take
$f_1$ is a rational function. Now we take ![]() $j-1$ derivatives of each side. Inductively, one sees that there exist rational functions
$j-1$ derivatives of each side. Inductively, one sees that there exist rational functions ![]() $f_j$ such that
$f_j$ such that
Setting ![]() $x= x_{k,r}=\widetilde \omega (r/k)$ then gives
$x= x_{k,r}=\widetilde \omega (r/k)$ then gives
With (4.9), we can use repeated application of the product rule to bound
 \begin{align*} \partial_k^{j} x_{k,r} &= \partial_k^{j} \widetilde{\omega}(r/k)\\ &= -\partial_k^{j-1} \widetilde{\omega}^\prime (r/k)\bigg(\frac{r}{k^2}\bigg)\\ &\ll \widetilde{\omega}^{(j)} (r/k)\bigg(\frac{r}{k^2}\bigg)^{j} + \widetilde{\omega}^\prime (r/k)\bigg(\frac{r}{k^{1+j}}\bigg)\\ &\ll x_{k,r}^{j+1} f_j(\log(x_{k,r}))\bigg(\frac{r}{k^2}\bigg)^{j} + x_{k,r}^2 f_1(\log(x_{k,r}))\bigg(\frac{r}{k^{1+j}}\bigg). \end{align*}
\begin{align*} \partial_k^{j} x_{k,r} &= \partial_k^{j} \widetilde{\omega}(r/k)\\ &= -\partial_k^{j-1} \widetilde{\omega}^\prime (r/k)\bigg(\frac{r}{k^2}\bigg)\\ &\ll \widetilde{\omega}^{(j)} (r/k)\bigg(\frac{r}{k^2}\bigg)^{j} + \widetilde{\omega}^\prime (r/k)\bigg(\frac{r}{k^{1+j}}\bigg)\\ &\ll x_{k,r}^{j+1} f_j(\log(x_{k,r}))\bigg(\frac{r}{k^2}\bigg)^{j} + x_{k,r}^2 f_1(\log(x_{k,r}))\bigg(\frac{r}{k^{1+j}}\bigg). \end{align*}
Now recall that ![]() $k \asymp e^{u}$,
$k \asymp e^{u}$, ![]() $x_{k,r} \asymp e^{q}$, and
$x_{k,r} \asymp e^{q}$, and ![]() $r \asymp e^{u-q}q^{A-1}$, thus
$r \asymp e^{u-q}q^{A-1}$, thus
 \begin{align*} \partial_k^{j} x_{k,r} &\ll \bigg(e^{q(j+1)} \bigg(\frac{e^{u-q}}{e^{2u}}\bigg)^{j} + e^{2q}\bigg(\frac{e^{u-q}}{e^{(1+j)u}}\bigg)\bigg)Q^{O(1)}\\ &\ll e^{q-ju}Q^{O(1)}. \end{align*}
\begin{align*} \partial_k^{j} x_{k,r} &\ll \bigg(e^{q(j+1)} \bigg(\frac{e^{u-q}}{e^{2u}}\bigg)^{j} + e^{2q}\bigg(\frac{e^{u-q}}{e^{(1+j)u}}\bigg)\bigg)Q^{O(1)}\\ &\ll e^{q-ju}Q^{O(1)}. \end{align*}
Hence, ![]() $\partial _k^{(j)} \mathfrak {N}_q(x_{k,r}) \ll e^{-ju} Q^{O(1)}$.
$\partial _k^{(j)} \mathfrak {N}_q(x_{k,r}) \ll e^{-ju} Q^{O(1)}$.
The same argument suffices to prove that ![]() $\partial _k^{j} (1/\sqrt {|\omega ^{\prime \prime }(x_{k,r})|}) \ll e^{q-ju} Q^{O(1)}$.
$\partial _k^{j} (1/\sqrt {|\omega ^{\prime \prime }(x_{k,r})|}) \ll e^{q-ju} Q^{O(1)}$.
4.4 Second application of the  $B$-process
$B$-process
We now apply the ![]() $B$-process in the
$B$-process in the ![]() $k$-variable. At the present stage, the phase function is
$k$-variable. At the present stage, the phase function is ![]() $\phi (k,r)+ks$. Thus, for
$\phi (k,r)+ks$. Thus, for ![]() $h \in \mathbb {Z}$, let
$h \in \mathbb {Z}$, let ![]() $\mu = \mu _{h,r,s}$ be the unique stationary point of
$\mu = \mu _{h,r,s}$ be the unique stationary point of ![]() $k \mapsto \phi (k,r) - (h-s)k$. Namely,
$k \mapsto \phi (k,r) - (h-s)k$. Namely,
After the second application of the ![]() $B$-process, the phase will be transformed to
$B$-process, the phase will be transformed to
With that, let (again for ![]() $u >0)$
$u >0)$
 \begin{equation} \mathcal{E}^{(\mathrm{BB})}_{q,u}(s):= \frac{1}{N} \sum_{r\ge 0}\sum_{h \ge 0} \widehat{f} \bigg(\frac{\mu}{N}\bigg)\mathfrak{K}_u(\mu)\mathfrak{N}_{q}(x_{\mu,r}) \frac{1}{\sqrt{|\mu \omega^{\prime\prime}(x_{\mu,r}) \cdot (\partial_{\mu\mu}\phi)(\mu,r) |}} e(\Phi(h,r,s)). \end{equation}
\begin{equation} \mathcal{E}^{(\mathrm{BB})}_{q,u}(s):= \frac{1}{N} \sum_{r\ge 0}\sum_{h \ge 0} \widehat{f} \bigg(\frac{\mu}{N}\bigg)\mathfrak{K}_u(\mu)\mathfrak{N}_{q}(x_{\mu,r}) \frac{1}{\sqrt{|\mu \omega^{\prime\prime}(x_{\mu,r}) \cdot (\partial_{\mu\mu}\phi)(\mu,r) |}} e(\Phi(h,r,s)). \end{equation} We can now apply the ![]() $B$-process for a second time and conclude the following proposition.
$B$-process for a second time and conclude the following proposition.
Proposition 4.5 We have
uniformly for any non-degenerate ![]() $(q,u)\in \mathscr {G}(N)$.
$(q,u)\in \mathscr {G}(N)$.
Before we can prove the above proposition, we need some preparations. Note that
If ![]() $u-q+(A-1)\log q<-10$ then
$u-q+(A-1)\log q<-10$ then ![]() $10 A e^{u-q}q^{A-1}=10 Ae^{-10 A}\leq 0.6$. Hence, there is no stationary point in the first application of the
$10 A e^{u-q}q^{A-1}=10 Ae^{-10 A}\leq 0.6$. Hence, there is no stationary point in the first application of the ![]() $B$-process. Thus, the contribution from this regime is disposed of by the first
$B$-process. Thus, the contribution from this regime is disposed of by the first ![]() $B$-process. Therefore, from now on we assume that
$B$-process. Therefore, from now on we assume that
4.5 Non-essential regimes
In this section we estimate the contribution from regimes where ![]() $u$ is smaller by a power of a logarithm than the top scale
$u$ is smaller by a power of a logarithm than the top scale ![]() $Q$. We shall see that this regime can be disposed of. More precisely, let
$Q$. We shall see that this regime can be disposed of. More precisely, let
We shall see that contribution ![]() $\mathcal {T}(N)$ is negligible by showing that the function
$\mathcal {T}(N)$ is negligible by showing that the function
has a small ![]() $\Vert \cdot \Vert _{\infty }$-norm (in the
$\Vert \cdot \Vert _{\infty }$-norm (in the ![]() $s\in [0,1]$ variable). To prove this, we need to ensure that in
$s\in [0,1]$ variable). To prove this, we need to ensure that in
 \[ \mathcal{E}_{q,u}^{(\mathrm{B})}(s)=\frac{e(-1/8)}{N}\sum_{r\geq0} \sum_{k\geq0}\Psi_{q,u}(k,r,s)e(\phi(k,r)-ks) \]
\[ \mathcal{E}_{q,u}^{(\mathrm{B})}(s)=\frac{e(-1/8)}{N}\sum_{r\geq0} \sum_{k\geq0}\Psi_{q,u}(k,r,s)e(\phi(k,r)-ks) \]
the amplitude function
has a suitably good decay in ![]() $k$.
$k$.
Lemma 4.6 If (4.12) holds, then
uniformly for ![]() $r$ and
$r$ and ![]() $s$ in the prescribed ranges.
$s$ in the prescribed ranges.
Proof. First, use the triangle inequality to bound
 \begin{align*} \Vert k\mapsto\partial_{k}\Psi_{q,u}(k,r,s)\Vert_{L^{1}(\mathbb{R})} &\ll \bigg\Vert \partial_k\bigg\{\frac{\mathfrak{N}_{q}(x_{k,r}) \mathfrak{K}_{u}(k)}{\sqrt{|k\omega''(x_{k,r})|}}\bigg\} \widehat{f}\bigg(\frac{k}{N}\bigg)\bigg\Vert_{L^{1}(\mathbb{R})} \\ &\quad +\bigg\Vert \frac{\mathfrak{N}_{q}(x_{k,r}) \mathfrak{K}_{u}(k)}{\sqrt{|k\omega''(x_{k,r})|}} \partial_k\widehat{f}\bigg(\frac{k}{N}\bigg)\bigg\Vert_{L^{1}(\mathbb{R})}. \end{align*}
\begin{align*} \Vert k\mapsto\partial_{k}\Psi_{q,u}(k,r,s)\Vert_{L^{1}(\mathbb{R})} &\ll \bigg\Vert \partial_k\bigg\{\frac{\mathfrak{N}_{q}(x_{k,r}) \mathfrak{K}_{u}(k)}{\sqrt{|k\omega''(x_{k,r})|}}\bigg\} \widehat{f}\bigg(\frac{k}{N}\bigg)\bigg\Vert_{L^{1}(\mathbb{R})} \\ &\quad +\bigg\Vert \frac{\mathfrak{N}_{q}(x_{k,r}) \mathfrak{K}_{u}(k)}{\sqrt{|k\omega''(x_{k,r})|}} \partial_k\widehat{f}\bigg(\frac{k}{N}\bigg)\bigg\Vert_{L^{1}(\mathbb{R})}. \end{align*}
Since ![]() $\widehat {f}$ has bounded derivative, the term on the right can be bounded by
$\widehat {f}$ has bounded derivative, the term on the right can be bounded by ![]() $1/N$ times the sup norm times
$1/N$ times the sup norm times ![]() $e^{u}$. Since
$e^{u}$. Since ![]() $\widehat {f}(\frac {k}{N})$ is bounded, and
$\widehat {f}(\frac {k}{N})$ is bounded, and ![]() $\frac {\mathfrak {N}_{q}(x_{k,r}) \mathfrak {K}_{u}(k)}{\sqrt {|k\omega ''(x_{k,r})|}}$ changes sign finitely many times, we can apply the fundamental theorem of calculus and bound the whole by
$\frac {\mathfrak {N}_{q}(x_{k,r}) \mathfrak {K}_{u}(k)}{\sqrt {|k\omega ''(x_{k,r})|}}$ changes sign finitely many times, we can apply the fundamental theorem of calculus and bound the whole by
 \[ \Vert k\mapsto\partial_{k}\Psi_{q,u}(k,r,s)\Vert_{L^{1}(\mathbb{R})} \ll \bigg\Vert k \mapsto \frac{1}{\sqrt{|k\omega''(x_{k,r})|}}\bigg\Vert_{L^{\infty}(\mathbb{R})}. \]
\[ \Vert k\mapsto\partial_{k}\Psi_{q,u}(k,r,s)\Vert_{L^{1}(\mathbb{R})} \ll \bigg\Vert k \mapsto \frac{1}{\sqrt{|k\omega''(x_{k,r})|}}\bigg\Vert_{L^{\infty}(\mathbb{R})}. \]
Now we are in the position to prove that the contribution from (4.13) is negligible thanks to a second derivative test. This is one of the places where, in contrast to the monomial case, we only win by a logarithmic factor. Moreover, this logarithmic saving goes to ![]() $0$ as
$0$ as ![]() $A$ approaches
$A$ approaches ![]() $1$.
$1$.
Lemma 4.7 The oscillatory integral
satisfies the bound
uniformly in ![]() $h,$ and
$h,$ and ![]() $r$ in ranges prescribed by
$r$ in ranges prescribed by ![]() $\Psi$.
$\Psi$.
Proof. We aim to apply van der Corput's lemma (Lemma 2.3) for a second derivative bound. For that, first note that ![]() $\partial _{t}\phi (t,r)=\omega (x_{t,r})+t\partial _{t}(\omega (x_{t,r}))-r\partial _{t}(x_{t,r})$. Now, since
$\partial _{t}\phi (t,r)=\omega (x_{t,r})+t\partial _{t}(\omega (x_{t,r}))-r\partial _{t}(x_{t,r})$. Now, since
it follows that
Now we bound the second derivative of ![]() $\phi (t,r)-t(s+h)$. By (4.16) and (4.17), we have
$\phi (t,r)-t(s+h)$. By (4.16) and (4.17), we have
Thus,
Taking ![]() $x_{t,r}\asymp e^{q}$ into account gives
$x_{t,r}\asymp e^{q}$ into account gives
The upshot, by van der Corput's lemma (Lemma 2.3), is that
Now we are in the position to prove the following lemma.
Lemma 4.8 We have that, as a function of ![]() $s\in [0,1]$, the sup norm
$s\in [0,1]$, the sup norm ![]() $\Vert T_{N}\Vert _{\infty }\ll (\log N)^{-8A}$.
$\Vert T_{N}\Vert _{\infty }\ll (\log N)^{-8A}$.
Proof. Note that
 \begin{equation} \mathcal{E}_{q,u}^{(\mathrm{B})}(s)\ll\frac{1}{N}\sum_{r\asymp e^{u-q}q^{A-1}} \vert\Xi(r)\vert, \quad\mathrm{where}\ \Xi(r):=\sum_{k > 0}\Psi_{q,u}(k,r,s)e(\phi(k,r)-ks).\end{equation}
\begin{equation} \mathcal{E}_{q,u}^{(\mathrm{B})}(s)\ll\frac{1}{N}\sum_{r\asymp e^{u-q}q^{A-1}} \vert\Xi(r)\vert, \quad\mathrm{where}\ \Xi(r):=\sum_{k > 0}\Psi_{q,u}(k,r,s)e(\phi(k,r)-ks).\end{equation}By Poisson summation,
We decompose the right-hand side into the contribution ![]() $\Xi _{1}(r)$ coming from
$\Xi _{1}(r)$ coming from ![]() $\vert h\vert >(4Q)^{A}$, and a contribution
$\vert h\vert >(4Q)^{A}$, and a contribution ![]() $\Xi _{2}(r)$ from the regime
$\Xi _{2}(r)$ from the regime ![]() $\vert h\vert \leq (4Q)^{A}$. Next, we argue that
$\vert h\vert \leq (4Q)^{A}$. Next, we argue that ![]() $\Xi _{1}(r)$ can be disposed of by partial integration. Because
$\Xi _{1}(r)$ can be disposed of by partial integration. Because ![]() $x_{k,r}\leq 2N$, we have
$x_{k,r}\leq 2N$, we have
Note for ![]() $\vert h\vert > (4Q)^{A}$, by (4.17), that the inequality
$\vert h\vert > (4Q)^{A}$, by (4.17), that the inequality
holds true uniformly in ![]() $r$ and
$r$ and ![]() $s$. As a result, partial integration yields, for any constant
$s$. As a result, partial integration yields, for any constant ![]() $C>0$, the bound
$C>0$, the bound
Therefore,
Recall that we have ![]() $q\geq {1/(m + 1)} Q$. Thus, taking
$q\geq {1/(m + 1)} Q$. Thus, taking ![]() $C$ to be large and using Lemma 4.6, we deduce that
$C$ to be large and using Lemma 4.6, we deduce that
for any constant ![]() $C_{1}>0$. All in all, we have shown so far that
$C_{1}>0$. All in all, we have shown so far that
In ![]() $\Xi _{2}(r)$ there are
$\Xi _{2}(r)$ there are ![]() $O(Q^{A})$ choices of
$O(Q^{A})$ choices of ![]() $h$. By using Lemma 4.7 we conclude
$h$. By using Lemma 4.7 we conclude
By combining (4.20) and (4.21), we deduce from (4.19) that
 \begin{align*} \Vert \mathcal{E}_{q,u}^{(\mathrm{B})}(\cdot)\Vert _{\infty}\ll \frac{1}{N}\sum_{r\asymp e^{u-q}q^{A-1}}e^{q}q^{1-A} Q^{A}\ll \frac{1}{N}e^{u} Q^{A}. \end{align*}
\begin{align*} \Vert \mathcal{E}_{q,u}^{(\mathrm{B})}(\cdot)\Vert _{\infty}\ll \frac{1}{N}\sum_{r\asymp e^{u-q}q^{A-1}}e^{q}q^{1-A} Q^{A}\ll \frac{1}{N}e^{u} Q^{A}. \end{align*}
As a result,
 \begin{align*} \Vert T_{N}(\cdot)\Vert_\infty &\ll\frac{1}{N}\sum_{(u,q)\in\mathcal{T}(N)}e^{u}Q^{A}\ll \frac{1}{N}\sum_{u\leq\log N-10A\log\log N}e^{u}Q^{A+1}\\ &\ll\frac{1}{(\log N)^{10A}}(\log N)^{A+1}\ll\frac{1}{(\log N)^{8A}}. \end{align*}
\begin{align*} \Vert T_{N}(\cdot)\Vert_\infty &\ll\frac{1}{N}\sum_{(u,q)\in\mathcal{T}(N)}e^{u}Q^{A}\ll \frac{1}{N}\sum_{u\leq\log N-10A\log\log N}e^{u}Q^{A+1}\\ &\ll\frac{1}{(\log N)^{10A}}(\log N)^{A+1}\ll\frac{1}{(\log N)^{8A}}. \end{align*}
4.6 Essential regimes
We are now ready to apply our stationary phase expansion (Proposition 2.1), and thus effectively apply the ![]() $B$-process a second time. Recall that after applying Poisson summation, the phase will be
$B$-process a second time. Recall that after applying Poisson summation, the phase will be ![]() $\psi _{r,h}(t) = \psi (t): = \phi (t,r) - t(h-s)$. Let
$\psi _{r,h}(t) = \psi (t): = \phi (t,r) - t(h-s)$. Let
Furthermore, define
where ![]() $p_0(\mu ) = e(1/8) W_{q,u}(\mu )$. Note that, by (4.18), one can bound
$p_0(\mu ) = e(1/8) W_{q,u}(\mu )$. Note that, by (4.18), one can bound
Hence, let
and set
 \[ E_{q,u}^{\mathrm{(BB)}}(s):=\frac{e(-1/8)}{N}\sum_{r\geq0}\sum_{h\geq0}P_{q,u}(h,r,s). \]
\[ E_{q,u}^{\mathrm{(BB)}}(s):=\frac{e(-1/8)}{N}\sum_{r\geq0}\sum_{h\geq0}P_{q,u}(h,r,s). \]
Before proving Proposition 4.5 we need the following lemma.
Lemma 4.9 For any ![]() $c\in [0,1]$ and any
$c\in [0,1]$ and any ![]() $M>10$, we have the bound
$M>10$, we have the bound
Proof. Decomposing into intervals where ![]() $\Vert c+s\Vert ^{-1}\leq M$ as well as intervals where
$\Vert c+s\Vert ^{-1}\leq M$ as well as intervals where ![]() $\Vert c+s\Vert ^{-1}>M$ and then using straightforward estimates implies the claimed bound.
$\Vert c+s\Vert ^{-1}>M$ and then using straightforward estimates implies the claimed bound.
We can now prove Proposition 4.5.
Proof Proof of Proposition 4.5
Fix ![]() $s \in [0,1]$ and recall the definition of
$s \in [0,1]$ and recall the definition of ![]() $I_{q,u}(h,r)$ from (4.14). Then, by Poisson summation,
$I_{q,u}(h,r)$ from (4.14). Then, by Poisson summation,
 \[ \mathcal{E}_{q,u}^{\mathrm{(B)}}(s)=\frac{e(-1/8)}{N}\sum_{r\geq0}\sum_{h\in\mathbb{Z}}I_{q,u}(h,r). \]
\[ \mathcal{E}_{q,u}^{\mathrm{(B)}}(s)=\frac{e(-1/8)}{N}\sum_{r\geq0}\sum_{h\in\mathbb{Z}}I_{q,u}(h,r). \]
Let ![]() $[a,b]:=\operatorname {supp}(\mathfrak {K}_u)$, and
$[a,b]:=\operatorname {supp}(\mathfrak {K}_u)$, and
We decompose the ![]() $h$-summation into three different ranges:
$h$-summation into three different ranges:
where the first contribution ![]() $\mathfrak {C}_{1}(r,s)$ is where
$\mathfrak {C}_{1}(r,s)$ is where ![]() $m_{r}(h)=0$, the second contribution
$m_{r}(h)=0$, the second contribution ![]() $\mathfrak {C}_{2}(r,s)$ is where
$\mathfrak {C}_{2}(r,s)$ is where ![]() $0< m_{r}(k)\leq N^{\varepsilon }$, and the third contribution
$0< m_{r}(k)\leq N^{\varepsilon }$, and the third contribution ![]() $\mathfrak {C}_{3}(r,s)$ is where
$\mathfrak {C}_{3}(r,s)$ is where ![]() $m_{r}(h)\geq N^{\varepsilon }$. Integration by parts shows that
$m_{r}(h)\geq N^{\varepsilon }$. Integration by parts shows that
Next, we handle ![]() $\mathfrak {C}_{1}(r,s)$. To this end, we shall apply Proposition 2.1, in the notation of which we have
$\mathfrak {C}_{1}(r,s)$. To this end, we shall apply Proposition 2.1, in the notation of which we have
The decay of the amplitude function was shown in Lemma 4.4; the decay of the phase function follows from a short calculation we omit. Next, since we have disposed of the inessential regimes, we see
Furthermore,
 \[ \frac{\Omega_{\psi}}{\Lambda_{\psi}^{1/2}}Z^{\frac{\delta}{2}}= \frac{e^{\frac{u}{2}}}{q^{(1/2)A}}Z^{\frac{\delta}{2}} \asymp\frac{e^{u(\frac{1}{2}+\delta)}}{q^{(1/2)A + (\delta/2)(A-1)}}.\]
\[ \frac{\Omega_{\psi}}{\Lambda_{\psi}^{1/2}}Z^{\frac{\delta}{2}}= \frac{e^{\frac{u}{2}}}{q^{(1/2)A}}Z^{\frac{\delta}{2}} \asymp\frac{e^{u(\frac{1}{2}+\delta)}}{q^{(1/2)A + (\delta/2)(A-1)}}.\]
Hence, taking ![]() $\delta :=1/11$ is compatible with the assumption (2.1). Thus,
$\delta :=1/11$ is compatible with the assumption (2.1). Thus,
Now we bound ![]() $\mathfrak {C}_{2}(r,s)$. First note that
$\mathfrak {C}_{2}(r,s)$. First note that ![]() $\omega (x_{t,r})$ is monotonic in
$\omega (x_{t,r})$ is monotonic in ![]() $t$. To see this, set the derivative equal to
$t$. To see this, set the derivative equal to ![]() $0$:
$0$:
However, since ![]() $x_{t,r}\asymp e^q$, this implies
$x_{t,r}\asymp e^q$, this implies ![]() $\omega ^\prime (r/k) =0$, which is a contradiction. Thus, by van der Corput's lemma (Lemma 2.3) for the first derivative, and monotonicity, we have
$\omega ^\prime (r/k) =0$, which is a contradiction. Thus, by van der Corput's lemma (Lemma 2.3) for the first derivative, and monotonicity, we have
where we used (4.18) and the fact that ![]() $\partial _t \phi (t,r) = \omega (x_{t,r})$. Notice that
$\partial _t \phi (t,r) = \omega (x_{t,r})$. Notice that
 \[ \bigg\Vert \frac{1}{N}\sum_{r\geq0}\mathfrak{C}_{2}(r,\cdot)\bigg\Vert_{L^{m}}^{m} \ll\bigg\Vert \frac{1}{N}\sum_{r\geq0}\mathfrak{C}_{2}(r,\cdot) \bigg\Vert _{\infty}^{m-1}\bigg\Vert \frac{1}{N} \sum_{r\geq0}\mathfrak{C}_{2}(r,\cdot)\bigg\Vert_{L^{1}}. \]
\[ \bigg\Vert \frac{1}{N}\sum_{r\geq0}\mathfrak{C}_{2}(r,\cdot)\bigg\Vert_{L^{m}}^{m} \ll\bigg\Vert \frac{1}{N}\sum_{r\geq0}\mathfrak{C}_{2}(r,\cdot) \bigg\Vert _{\infty}^{m-1}\bigg\Vert \frac{1}{N} \sum_{r\geq0}\mathfrak{C}_{2}(r,\cdot)\bigg\Vert_{L^{1}}. \]
By (4.15) we see that
 \[ \bigg\Vert\frac{1}{N}\sum_{r\geq0}\mathfrak{C}_{2}(r,s)\bigg\Vert_{\infty}^{m-1}\ll N^{O(\varepsilon)}. \]
\[ \bigg\Vert\frac{1}{N}\sum_{r\geq0}\mathfrak{C}_{2}(r,s)\bigg\Vert_{\infty}^{m-1}\ll N^{O(\varepsilon)}. \]
Hence, it remains to estimate
 \[ N^{O(\varepsilon)}\sum_{r\asymp e^{u-q}q^{A-1}} \frac{1}{\sqrt{N}}\int_{0}^{1}\min(\Vert \omega(x_{a,r})+s\Vert^{-1},N^{\frac{1}{2}+o(1)})\,{d}s. \]
\[ N^{O(\varepsilon)}\sum_{r\asymp e^{u-q}q^{A-1}} \frac{1}{\sqrt{N}}\int_{0}^{1}\min(\Vert \omega(x_{a,r})+s\Vert^{-1},N^{\frac{1}{2}+o(1)})\,{d}s. \]
By exploiting Lemma 4.9 we see that
 \[ \bigg\Vert \frac{1}{N}\sum_{r\geq0}\mathfrak{C}_{2}(r,\cdot)\bigg\Vert _{L^{m}}^m \ll \sum_{r\asymp e^{u-q}q^{A-1}}\frac{N^{o(1)}}{\sqrt{N}}\ll N^{o(1)-\frac{1}{2}} \]
\[ \bigg\Vert \frac{1}{N}\sum_{r\geq0}\mathfrak{C}_{2}(r,\cdot)\bigg\Vert _{L^{m}}^m \ll \sum_{r\asymp e^{u-q}q^{A-1}}\frac{N^{o(1)}}{\sqrt{N}}\ll N^{o(1)-\frac{1}{2}} \]
which implies the claim.
Finally, it remains to show that
from which we can apply the triangle inequality to conclude Proposition 4.5. For this, recall the bounds (4.22). Since ![]() $\mathcal {E}_{q,u}^{(\mathrm {BB})}$ is simply the term arising from
$\mathcal {E}_{q,u}^{(\mathrm {BB})}$ is simply the term arising from ![]() $p_0(\mu )$, we have that
$p_0(\mu )$, we have that
 \[ \|\mathcal{E}^{(\mathrm{BB})}_{q,u}(\cdot) - E^{(\mathrm{BB})}_{q,u}(\cdot)\|_{L^m}^m \ll \frac{1}{N}\sum_{r\in \mathbb{Z}} p_1 \ll \frac{e^{u-q/2}N^\varepsilon}{N}. \]
\[ \|\mathcal{E}^{(\mathrm{BB})}_{q,u}(\cdot) - E^{(\mathrm{BB})}_{q,u}(\cdot)\|_{L^m}^m \ll \frac{1}{N}\sum_{r\in \mathbb{Z}} p_1 \ll \frac{e^{u-q/2}N^\varepsilon}{N}. \]
From here the bound follows from the ranges of ![]() $q$ and
$q$ and ![]() $u$.
$u$.
Before proceeding, we note that (4.10) can be simplified. In particular, we have the following lemma.
Lemma 4.10 Given, ![]() $h$,
$h$, ![]() $r$, and
$r$, and ![]() $s$ as above, we have
$s$ as above, we have
and
Proof. Recall ![]() $x_{k,r}=\tilde {\omega }(\frac {r}{k})$. Now, to compute
$x_{k,r}=\tilde {\omega }(\frac {r}{k})$. Now, to compute ![]() $\mu$, we have
$\mu$, we have
Consider first
Furthermore, since ![]() $\mu = \widetilde {\omega }(\omega ^\prime (\mu ))$, we may differentiate both sides and then change variables to see that
$\mu = \widetilde {\omega }(\omega ^\prime (\mu ))$, we may differentiate both sides and then change variables to see that
Hence,
Hence,
 \begin{align*} 0 &= \omega(x_{\mu,r}) - r \bigg(\omega\bigg(\widetilde{\omega}\bigg(\frac{r}{\mu}\bigg)\bigg) \frac{r}{\mu^2 \omega^{\prime\prime}(\widetilde{\omega}(r/\mu))}\bigg) + \omega\bigg(\widetilde{\omega}\bigg(\frac{r}{\mu}\bigg)\bigg) \frac{r^2}{\mu^2 \omega^{\prime\prime}(\widetilde{\omega}(r/\mu))} - (h-s)\\ &= \omega(x_{\mu,r}) - (h-s). \end{align*}
\begin{align*} 0 &= \omega(x_{\mu,r}) - r \bigg(\omega\bigg(\widetilde{\omega}\bigg(\frac{r}{\mu}\bigg)\bigg) \frac{r}{\mu^2 \omega^{\prime\prime}(\widetilde{\omega}(r/\mu))}\bigg) + \omega\bigg(\widetilde{\omega}\bigg(\frac{r}{\mu}\bigg)\bigg) \frac{r^2}{\mu^2 \omega^{\prime\prime}(\widetilde{\omega}(r/\mu))} - (h-s)\\ &= \omega(x_{\mu,r}) - (h-s). \end{align*}
Hence, ![]() $\omega (\widetilde {\omega }(r/\mu )) = h-s$. Solving for
$\omega (\widetilde {\omega }(r/\mu )) = h-s$. Solving for ![]() $\mu$ gives
$\mu$ gives
Moreover, we can simplify the phase as follows:
 \begin{align*} \Phi(h,r,s) &= \phi(\mu,r) - (h-s)\mu\\ &= \mu \omega(x_{\mu,r}) - r x_{\mu,r} - (h-s)\mu\\ &= \mu \omega(\widetilde{\omega}(r/\mu)) - r \widetilde{\omega}(r/\mu) - (h-s)\mu\\ &= \frac{r(h-s)}{\omega^\prime(\omega^{-1}(h-s))} - r \omega^{-1}(h-s) - (h-s) \frac{r}{\omega^\prime(\omega^{-1}(h-s))}\\ &= - r \omega^{-1}(h-s). \end{align*}
\begin{align*} \Phi(h,r,s) &= \phi(\mu,r) - (h-s)\mu\\ &= \mu \omega(x_{\mu,r}) - r x_{\mu,r} - (h-s)\mu\\ &= \mu \omega(\widetilde{\omega}(r/\mu)) - r \widetilde{\omega}(r/\mu) - (h-s)\mu\\ &= \frac{r(h-s)}{\omega^\prime(\omega^{-1}(h-s))} - r \omega^{-1}(h-s) - (h-s) \frac{r}{\omega^\prime(\omega^{-1}(h-s))}\\ &= - r \omega^{-1}(h-s). \end{align*}
Turning now to (4.23), we note that since, by the definition of ![]() $\mu$, we have that
$\mu$, we have that ![]() $\partial _\mu \phi (\mu,r) = h-s$ and
$\partial _\mu \phi (\mu,r) = h-s$ and ![]() $h-s = \omega (\widetilde {\omega }(r/\mu ))$, we may differentiate both sides of the former to deduce that
$h-s = \omega (\widetilde {\omega }(r/\mu ))$, we may differentiate both sides of the former to deduce that
 \begin{align*} \partial_{\mu\mu}\phi(\mu,r) &= \partial_\mu(\omega (\widetilde{\omega}(r/\mu)))\\ &= \omega^\prime(\widetilde{\omega}(r/\mu)) \widetilde{\omega}^\prime(r/\mu) (- r/\mu^2)\\ &= - (r^2/\mu^3) \widetilde{\omega}^\prime(r/\mu). \end{align*}
\begin{align*} \partial_{\mu\mu}\phi(\mu,r) &= \partial_\mu(\omega (\widetilde{\omega}(r/\mu)))\\ &= \omega^\prime(\widetilde{\omega}(r/\mu)) \widetilde{\omega}^\prime(r/\mu) (- r/\mu^2)\\ &= - (r^2/\mu^3) \widetilde{\omega}^\prime(r/\mu). \end{align*}
Now, using (4.24), we conclude that
 \begin{align*} \mu \omega^{\prime\prime}(x_{r,\mu}) \cdot (\partial_{\mu\mu}\phi)(\mu,r) &= -\mu \omega^{\prime\prime}(\widetilde{\omega}(r/\mu)) (r^2/\mu^3) \widetilde{\omega}^\prime(r/\mu)\\ &= -(r^2/\mu^2) \omega^{\prime\prime}(\widetilde{\omega}(r/\mu)) \frac{1}{\omega^{\prime\prime}(\widetilde{\omega}(r/\mu))} = -\frac{r^2}{\mu^2}. \end{align*}
\begin{align*} \mu \omega^{\prime\prime}(x_{r,\mu}) \cdot (\partial_{\mu\mu}\phi)(\mu,r) &= -\mu \omega^{\prime\prime}(\widetilde{\omega}(r/\mu)) (r^2/\mu^3) \widetilde{\omega}^\prime(r/\mu)\\ &= -(r^2/\mu^2) \omega^{\prime\prime}(\widetilde{\omega}(r/\mu)) \frac{1}{\omega^{\prime\prime}(\widetilde{\omega}(r/\mu))} = -\frac{r^2}{\mu^2}. \end{align*}
Applying Lemma 4.10 and inserting some definitions allows us to write
 \begin{equation} \mathcal{E}^{(\mathrm{BB})}_{q,u}(s)=\frac{1}{N}\sum_{r\ge 0}\sum_{h \ge 0} \widehat{f} \bigg(\frac{\mu}{N}\bigg)\mathfrak{K}_u(\mu)\mathfrak{N}_{q}(\widetilde{\omega}(r/\mu)) \frac{\mu}{r} e(-r\omega^{-1}(h-s)). \end{equation}
\begin{equation} \mathcal{E}^{(\mathrm{BB})}_{q,u}(s)=\frac{1}{N}\sum_{r\ge 0}\sum_{h \ge 0} \widehat{f} \bigg(\frac{\mu}{N}\bigg)\mathfrak{K}_u(\mu)\mathfrak{N}_{q}(\widetilde{\omega}(r/\mu)) \frac{\mu}{r} e(-r\omega^{-1}(h-s)). \end{equation} Returning now to the full ![]() $L^m$ norm, let
$L^m$ norm, let ![]() $\sigma _i := \sigma (u_i) := \frac {u_i}{|u_i|}$. Applying Propositions 4.3 and 4.5 and expanding the
$\sigma _i := \sigma (u_i) := \frac {u_i}{|u_i|}$. Applying Propositions 4.3 and 4.5 and expanding the ![]() $m$th power yields
$m$th power yields
 \begin{equation} \mathcal{F}(N) = \sum_{\sigma_1,\ldots,\sigma_m\in \{\pm 1\} } \sum_{\substack{(u_i,q_i) \in \mathscr{G}(N)\\ u_i>0}} \int_{0}^{1}\prod_{\substack{i\leq m\\ \sigma_i >0}} \mathcal{E}^{\mathrm{(BB)}}_{q_i, u_i}(s)\prod_{\substack{i\leq m\\ \sigma_i <0}} \overline{\mathcal{E}^{\mathrm{(BB)}}_{q_i, u_i}(s)}\,d s+ O(N^{-\varepsilon/2}). \end{equation}
\begin{equation} \mathcal{F}(N) = \sum_{\sigma_1,\ldots,\sigma_m\in \{\pm 1\} } \sum_{\substack{(u_i,q_i) \in \mathscr{G}(N)\\ u_i>0}} \int_{0}^{1}\prod_{\substack{i\leq m\\ \sigma_i >0}} \mathcal{E}^{\mathrm{(BB)}}_{q_i, u_i}(s)\prod_{\substack{i\leq m\\ \sigma_i <0}} \overline{\mathcal{E}^{\mathrm{(BB)}}_{q_i, u_i}(s)}\,d s+ O(N^{-\varepsilon/2}). \end{equation}
To simplify this expression, for a fixed ![]() $\boldsymbol {\mathbf {u}}$ and
$\boldsymbol {\mathbf {u}}$ and ![]() $\boldsymbol {\mathbf {q}}$, and
$\boldsymbol {\mathbf {q}}$, and ![]() $\boldsymbol {\mathbf {\mu }}=(\mu _1,\ldots,\mu _m)$, let
$\boldsymbol {\mathbf {\mu }}=(\mu _1,\ldots,\mu _m)$, let ![]() $\mathfrak {K}_{\boldsymbol {\mathbf {u}}}(\boldsymbol {\mathbf {\mu }}):= \prod _{i\leq m}\mathfrak {K}_{u_i}(\mu _i)$. The functions
$\mathfrak {K}_{\boldsymbol {\mathbf {u}}}(\boldsymbol {\mathbf {\mu }}):= \prod _{i\leq m}\mathfrak {K}_{u_i}(\mu _i)$. The functions ![]() $\mathfrak {N}_{\boldsymbol {\mathbf {q}}}(\boldsymbol {\mathbf {\mu }},s)$ and
$\mathfrak {N}_{\boldsymbol {\mathbf {q}}}(\boldsymbol {\mathbf {\mu }},s)$ and ![]() $\widehat {f}(\boldsymbol {\mathbf {\mu }}/N)$ are defined similarly. Aside from the error term, the right-hand side of (4.26) splits into a sum over
$\widehat {f}(\boldsymbol {\mathbf {\mu }}/N)$ are defined similarly. Aside from the error term, the right-hand side of (4.26) splits into a sum over
 \[ \mathcal{F}_{\boldsymbol{\mathbf{q}},\boldsymbol{\mathbf{u}}} := \frac{1}{N^m}\sum_{\boldsymbol{\mathbf{r}} \in \mathbb{Z}^m}\frac{1}{r_1r_2\cdots r_m} \int_0^1\sum_{\boldsymbol{\mathbf{h}}\in \mathbb{Z}^m}\mathfrak{K}_{\boldsymbol{\mathbf{u}}}(\boldsymbol{\mathbf{\mu}}) \mathfrak{N}_{\boldsymbol{\mathbf{q}}}(\boldsymbol{\mathbf{\mu}},s)A_{\boldsymbol{\mathbf{h}},\boldsymbol{\mathbf{r}}}(s) e(\varphi_{\boldsymbol{\mathbf{h}},\boldsymbol{\mathbf{r}}}(s))\,{d}s, \]
\[ \mathcal{F}_{\boldsymbol{\mathbf{q}},\boldsymbol{\mathbf{u}}} := \frac{1}{N^m}\sum_{\boldsymbol{\mathbf{r}} \in \mathbb{Z}^m}\frac{1}{r_1r_2\cdots r_m} \int_0^1\sum_{\boldsymbol{\mathbf{h}}\in \mathbb{Z}^m}\mathfrak{K}_{\boldsymbol{\mathbf{u}}}(\boldsymbol{\mathbf{\mu}}) \mathfrak{N}_{\boldsymbol{\mathbf{q}}}(\boldsymbol{\mathbf{\mu}},s)A_{\boldsymbol{\mathbf{h}},\boldsymbol{\mathbf{r}}}(s) e(\varphi_{\boldsymbol{\mathbf{h}},\boldsymbol{\mathbf{r}}}(s))\,{d}s, \]
where the phase function is given by
and where
Now we distinguish between two cases. First, the set of all ![]() $(\boldsymbol {\mathbf {r}},\boldsymbol {\mathbf {h}})$ where the phase
$(\boldsymbol {\mathbf {r}},\boldsymbol {\mathbf {h}})$ where the phase ![]() $\varphi _{\boldsymbol {\mathbf {h}},\boldsymbol {\mathbf {r}}}(s)$ vanishes identically, which we call the diagonal; and its complement, the off-diagonal. Let
$\varphi _{\boldsymbol {\mathbf {h}},\boldsymbol {\mathbf {r}}}(s)$ vanishes identically, which we call the diagonal; and its complement, the off-diagonal. Let
and let
 \[ \eta(\boldsymbol{\mathbf{r}},\boldsymbol{\mathbf{h}}):=\begin{cases} 1 & \mbox{if } (\boldsymbol{\mathbf{r}},\boldsymbol{\mathbf{h}}) \not\in \mathscr{A}, \\ 0 & \mbox{if } (\boldsymbol{\mathbf{r}},\boldsymbol{\mathbf{h}}) \in \mathscr{A}. \end{cases} \]
\[ \eta(\boldsymbol{\mathbf{r}},\boldsymbol{\mathbf{h}}):=\begin{cases} 1 & \mbox{if } (\boldsymbol{\mathbf{r}},\boldsymbol{\mathbf{h}}) \not\in \mathscr{A}, \\ 0 & \mbox{if } (\boldsymbol{\mathbf{r}},\boldsymbol{\mathbf{h}}) \in \mathscr{A}. \end{cases} \]
The diagonal, as we show, contributes the main term, while the off-diagonal contribution is negligible (see § 6).
5. Extracting the diagonal
First, we establish an asymptotic for the diagonal. The sums below range over ![]() $\boldsymbol {\mathbf {q}} \in [2Q]^m$,
$\boldsymbol {\mathbf {q}} \in [2Q]^m$, ![]() $\boldsymbol {\mathbf {u}}\in [-U,U]$, and
$\boldsymbol {\mathbf {u}}\in [-U,U]$, and ![]() $\boldsymbol {\mathbf {r}},\boldsymbol {\mathbf {h}}\in \mathbb {Z}$. Let
$\boldsymbol {\mathbf {r}},\boldsymbol {\mathbf {h}}\in \mathbb {Z}$. Let
 \[ \mathcal{D}_N = \frac{1}{N^m}\sum_{\boldsymbol{\mathbf{q}},\boldsymbol{\mathbf{u}},\boldsymbol{\mathbf{r}},\boldsymbol{\mathbf{h}} }(1-\eta(\boldsymbol{\mathbf{r}},\boldsymbol{\mathbf{h}})) \frac{1}{r_1r_2\cdots r_m} \int_0^1 \mathfrak{K}_{\boldsymbol{\mathbf{u}}}(\boldsymbol{\mathbf{\mu}}) \mathfrak{N}_{\boldsymbol{\mathbf{q}}}(\boldsymbol{\mathbf{\mu}},s) A_{\boldsymbol{\mathbf{h}},\boldsymbol{\mathbf{r}}}(s)\,{d}s. \]
\[ \mathcal{D}_N = \frac{1}{N^m}\sum_{\boldsymbol{\mathbf{q}},\boldsymbol{\mathbf{u}},\boldsymbol{\mathbf{r}},\boldsymbol{\mathbf{h}} }(1-\eta(\boldsymbol{\mathbf{r}},\boldsymbol{\mathbf{h}})) \frac{1}{r_1r_2\cdots r_m} \int_0^1 \mathfrak{K}_{\boldsymbol{\mathbf{u}}}(\boldsymbol{\mathbf{\mu}}) \mathfrak{N}_{\boldsymbol{\mathbf{q}}}(\boldsymbol{\mathbf{\mu}},s) A_{\boldsymbol{\mathbf{h}},\boldsymbol{\mathbf{r}}}(s)\,{d}s. \]
With that, the following lemma establishes the main asymptotic needed to prove Lemma 3.1 (and thus Theorem 1.2).
Lemma 5.1 We have
where the sum is over all non-isolating partitions of ![]() $[m]$, which we denote by
$[m]$, which we denote by ![]() $\mathcal {P} = (P_1, \ldots, P_d)$.
$\mathcal {P} = (P_1, \ldots, P_d)$.
Proof. Since the Fourier transform ![]() $\widehat {f}$ is assumed to have compact support, we can evaluate the sum over
$\widehat {f}$ is assumed to have compact support, we can evaluate the sum over ![]() $\boldsymbol {\mathbf {u}}$ and eliminate the factors
$\boldsymbol {\mathbf {u}}$ and eliminate the factors ![]() $\mathfrak {K}_{\boldsymbol {\mathbf {u}}}$. Hence,
$\mathfrak {K}_{\boldsymbol {\mathbf {u}}}$. Hence,
 \[ \mathcal{D}_N = \frac{1}{N^m}\sum_{\boldsymbol{\mathbf{q}},\boldsymbol{\mathbf{r}},\boldsymbol{\mathbf{h}}} 1(|\mu_i| >0) (1-\eta(\boldsymbol{\mathbf{r}},\boldsymbol{\mathbf{h}}))\frac{1}{r_1r_2\cdots r_m} \int_0^1 \mathfrak{N}_{\boldsymbol{\mathbf{q}}} (\boldsymbol{\mathbf{\mu}},s) A_{\boldsymbol{\mathbf{h}},\boldsymbol{\mathbf{r}}}(s)\,{d}s, \]
\[ \mathcal{D}_N = \frac{1}{N^m}\sum_{\boldsymbol{\mathbf{q}},\boldsymbol{\mathbf{r}},\boldsymbol{\mathbf{h}}} 1(|\mu_i| >0) (1-\eta(\boldsymbol{\mathbf{r}},\boldsymbol{\mathbf{h}}))\frac{1}{r_1r_2\cdots r_m} \int_0^1 \mathfrak{N}_{\boldsymbol{\mathbf{q}}} (\boldsymbol{\mathbf{\mu}},s) A_{\boldsymbol{\mathbf{h}},\boldsymbol{\mathbf{r}}}(s)\,{d}s, \]
where the indicator function takes care of the fact that we extracted the contribution when ![]() $k_i=0$.
$k_i=0$.
The condition that the phase is zero is equivalent to a condition on ![]() $\boldsymbol {\mathbf {h}}$ and
$\boldsymbol {\mathbf {h}}$ and ![]() $\boldsymbol {\mathbf {r}}$. Specifically, this happens in the following situation. Let
$\boldsymbol {\mathbf {r}}$. Specifically, this happens in the following situation. Let ![]() $\mathcal {P}$ be a non-isolating partition of
$\mathcal {P}$ be a non-isolating partition of ![]() $[m]$. We say that a vector
$[m]$. We say that a vector ![]() $(\boldsymbol {\mathbf {r}},\boldsymbol {\mathbf {h}})$ is
$(\boldsymbol {\mathbf {r}},\boldsymbol {\mathbf {h}})$ is ![]() $\mathcal {P}$-adjusted if for every
$\mathcal {P}$-adjusted if for every ![]() $P \in \mathcal {P}$ we have
$P \in \mathcal {P}$ we have ![]() $h_i = h_j$ for all
$h_i = h_j$ for all ![]() $i, j \in P$, and
$i, j \in P$, and ![]() $\sum _{i\in P} r_i = 0$. The diagonal is restricted to
$\sum _{i\in P} r_i = 0$. The diagonal is restricted to ![]() $\mathcal {P}$-adjusted vectors. Now
$\mathcal {P}$-adjusted vectors. Now
 \[ \chi_{\mathcal{P},1}(\boldsymbol{\mathbf{r}}):=\begin{cases} 1 & \mbox{if}\ \displaystyle\sum_{i\in P} r_i =0\ \text{for each}\ P \in \mathcal{P},\\ 0 & \mbox{otherwise}, \end{cases}\quad \chi_{\mathcal{P},2}(\boldsymbol{\mathbf{h}}):= \begin{cases} 1 & \mbox{if}\ h_i =h_j\ \text{for all}\ i,j \in P\in \mathcal{P},\\ 0 & \mbox{otherwise,} \end{cases} \]
\[ \chi_{\mathcal{P},1}(\boldsymbol{\mathbf{r}}):=\begin{cases} 1 & \mbox{if}\ \displaystyle\sum_{i\in P} r_i =0\ \text{for each}\ P \in \mathcal{P},\\ 0 & \mbox{otherwise}, \end{cases}\quad \chi_{\mathcal{P},2}(\boldsymbol{\mathbf{h}}):= \begin{cases} 1 & \mbox{if}\ h_i =h_j\ \text{for all}\ i,j \in P\in \mathcal{P},\\ 0 & \mbox{otherwise,} \end{cases} \]
where ![]() $\chi _{\mathcal {P},1}(\boldsymbol {\mathbf {r}})\chi _{\mathcal {P},2}(\boldsymbol {\mathbf {h}})$ encodes the condition that
$\chi _{\mathcal {P},1}(\boldsymbol {\mathbf {r}})\chi _{\mathcal {P},2}(\boldsymbol {\mathbf {h}})$ encodes the condition that ![]() $(\boldsymbol {\mathbf {r}},\boldsymbol {\mathbf {h}})$ is
$(\boldsymbol {\mathbf {r}},\boldsymbol {\mathbf {h}})$ is ![]() $\mathcal {P}$-adjusted. Thus, we may write
$\mathcal {P}$-adjusted. Thus, we may write
 \[ \mathcal{D}_N = \frac{1}{N^m}\sum_{\mathcal{P}\in \mathscr{P}_m} \sum_{\boldsymbol{\mathbf{q}},\boldsymbol{\mathbf{r}}, \boldsymbol{\mathbf{h}}} \chi_{\mathcal{P},1}(\boldsymbol{\mathbf{r}})\chi_{\mathcal{P},2}(\boldsymbol{\mathbf{h}})\frac{1}{r_1r_2\cdots r_m} \bigg(\int_0^1 \mathfrak{N}_{\boldsymbol{\mathbf{q}}}(\boldsymbol{\mathbf{\mu}}, s)\widehat{f} \bigg(\frac{\boldsymbol{\mathbf{\mu}}}{N}\bigg) \mu_1\mu_2\cdots \mu_m \,{d}s\bigg) +o(1). \]
\[ \mathcal{D}_N = \frac{1}{N^m}\sum_{\mathcal{P}\in \mathscr{P}_m} \sum_{\boldsymbol{\mathbf{q}},\boldsymbol{\mathbf{r}}, \boldsymbol{\mathbf{h}}} \chi_{\mathcal{P},1}(\boldsymbol{\mathbf{r}})\chi_{\mathcal{P},2}(\boldsymbol{\mathbf{h}})\frac{1}{r_1r_2\cdots r_m} \bigg(\int_0^1 \mathfrak{N}_{\boldsymbol{\mathbf{q}}}(\boldsymbol{\mathbf{\mu}}, s)\widehat{f} \bigg(\frac{\boldsymbol{\mathbf{\mu}}}{N}\bigg) \mu_1\mu_2\cdots \mu_m \,{d}s\bigg) +o(1). \]
Inserting the definition of ![]() $\mu _i$ then gives
$\mu _i$ then gives
 \[ \mathcal{D}_N = \frac{1}{N^m}\sum_{\mathcal{P}\in \mathscr{P}_m}\sum_{\boldsymbol{\mathbf{q}},\boldsymbol{\mathbf{r}}, \boldsymbol{\mathbf{h}}} \chi_{\mathcal{P},1}(\boldsymbol{\mathbf{r}})\chi_{\mathcal{P},2}(\boldsymbol{\mathbf{h}}) \int_0^1 \mathfrak{N}_{\boldsymbol{\mathbf{q}}} (\boldsymbol{\mathbf{\mu}},s)\widehat{f}\bigg(\frac{\boldsymbol{\mathbf{\mu}}}{N}\bigg) \prod_{i=1}^m \bigg(\frac{1}{\omega^\prime(\omega^{-1}(h_i-s))}\bigg) {d}s +o(1). \]
\[ \mathcal{D}_N = \frac{1}{N^m}\sum_{\mathcal{P}\in \mathscr{P}_m}\sum_{\boldsymbol{\mathbf{q}},\boldsymbol{\mathbf{r}}, \boldsymbol{\mathbf{h}}} \chi_{\mathcal{P},1}(\boldsymbol{\mathbf{r}})\chi_{\mathcal{P},2}(\boldsymbol{\mathbf{h}}) \int_0^1 \mathfrak{N}_{\boldsymbol{\mathbf{q}}} (\boldsymbol{\mathbf{\mu}},s)\widehat{f}\bigg(\frac{\boldsymbol{\mathbf{\mu}}}{N}\bigg) \prod_{i=1}^m \bigg(\frac{1}{\omega^\prime(\omega^{-1}(h_i-s))}\bigg) {d}s +o(1). \]
Now note that the ![]() $\boldsymbol {\mathbf {r}}$ variable only appears in
$\boldsymbol {\mathbf {r}}$ variable only appears in ![]() $\widehat {f}(\boldsymbol {\mathbf {\mu }}/N)$, that is,
$\widehat {f}(\boldsymbol {\mathbf {\mu }}/N)$, that is,
 \begin{align} \mathcal{D}_N &= \frac{1}{N^m}\sum_{\mathcal{P}\in \mathscr{P}_m} \sum_{P \in \mathcal{P}}\sum_{\boldsymbol{\mathbf{q}}, h}\int_0^1 \mathfrak{N}_{\boldsymbol{\mathbf{q}},P}(h) \bigg(\frac{1}{\omega^\prime(\omega^{-1}(h))}\bigg)^{|P|} \nonumber\\ &\quad \times \sum_{\substack{\boldsymbol{\mathbf{r}}\in \mathbb{Z}^{|P|}\\r_i \neq 0}} \chi(\boldsymbol{\mathbf{r}}) \widehat{f}\bigg(\frac{1}{N\omega^\prime(\omega^{-1}(h))} \boldsymbol{\mathbf{r}}\bigg){d}s(1+ o(1)), \end{align}
\begin{align} \mathcal{D}_N &= \frac{1}{N^m}\sum_{\mathcal{P}\in \mathscr{P}_m} \sum_{P \in \mathcal{P}}\sum_{\boldsymbol{\mathbf{q}}, h}\int_0^1 \mathfrak{N}_{\boldsymbol{\mathbf{q}},P}(h) \bigg(\frac{1}{\omega^\prime(\omega^{-1}(h))}\bigg)^{|P|} \nonumber\\ &\quad \times \sum_{\substack{\boldsymbol{\mathbf{r}}\in \mathbb{Z}^{|P|}\\r_i \neq 0}} \chi(\boldsymbol{\mathbf{r}}) \widehat{f}\bigg(\frac{1}{N\omega^\prime(\omega^{-1}(h))} \boldsymbol{\mathbf{r}}\bigg){d}s(1+ o(1)), \end{align}
where ![]() $\chi (\boldsymbol {\mathbf {r}})$ is
$\chi (\boldsymbol {\mathbf {r}})$ is ![]() $1$ if
$1$ if ![]() $\sum _{i=1}^{|P|} r_i = 0$ and where
$\sum _{i=1}^{|P|} r_i = 0$ and where ![]() $\mathfrak {N}_{\boldsymbol {\mathbf {q}},P}(h) = \prod _{i\in P}\mathfrak {N}_{q_i} (\mu _i, s)$. We can apply Euler's summation formula ([Reference ApostolApo76, Theorem 3.1]) to conclude that
$\mathfrak {N}_{\boldsymbol {\mathbf {q}},P}(h) = \prod _{i\in P}\mathfrak {N}_{q_i} (\mu _i, s)$. We can apply Euler's summation formula ([Reference ApostolApo76, Theorem 3.1]) to conclude that
 \begin{align*} \sum_{\substack{\boldsymbol{\mathbf{r}}\in \mathbb{Z}^{|P|}\\r_i \neq 0}}\chi(\boldsymbol{\mathbf{r}}) \widehat{f}\bigg(\frac{1}{N\omega^\prime(\omega^{-1}(h))}\boldsymbol{\mathbf{r}}\bigg)= \int_{\mathbb{R}^{|P|}} \chi(\boldsymbol{\mathbf{x}})\widehat{f}\bigg(\frac{1}{N\omega^\prime(\omega^{-1}(h))} \boldsymbol{\mathbf{x}}\bigg) {d}\boldsymbol{\mathbf{x}}(1+ o(1)). \end{align*}
\begin{align*} \sum_{\substack{\boldsymbol{\mathbf{r}}\in \mathbb{Z}^{|P|}\\r_i \neq 0}}\chi(\boldsymbol{\mathbf{r}}) \widehat{f}\bigg(\frac{1}{N\omega^\prime(\omega^{-1}(h))}\boldsymbol{\mathbf{r}}\bigg)= \int_{\mathbb{R}^{|P|}} \chi(\boldsymbol{\mathbf{x}})\widehat{f}\bigg(\frac{1}{N\omega^\prime(\omega^{-1}(h))} \boldsymbol{\mathbf{x}}\bigg) {d}\boldsymbol{\mathbf{x}}(1+ o(1)). \end{align*}
Changing variables then yields
note that ![]() $\chi (\boldsymbol {\mathbf {x}})$ fixes
$\chi (\boldsymbol {\mathbf {x}})$ fixes ![]() $x_{|P|} = - \sum _{i=1}^{|P|-1} x_i$. Plugging this into our (5.2) gives
$x_{|P|} = - \sum _{i=1}^{|P|-1} x_i$. Plugging this into our (5.2) gives
 \[ \mathcal{D}_N = \frac{1}{N^d}\sum_{\mathcal{P}\in \mathscr{P}_m}\sum_{P \in \mathcal{P}} \sum_{\boldsymbol{\mathbf{q}}, h} \mathfrak{N}_{\boldsymbol{\mathbf{q}},P}(h)\omega^\prime(\omega^{-1}(h)) \int_{\mathbb{R}^{|P|-1}} \widehat{f}(x_1, \ldots, x_{|P|-1}, -\boldsymbol{\mathbf{x}}\cdot \boldsymbol{\mathbf{1}}) \,d \boldsymbol{\mathbf{x}} (1+ o(1)). \]
\[ \mathcal{D}_N = \frac{1}{N^d}\sum_{\mathcal{P}\in \mathscr{P}_m}\sum_{P \in \mathcal{P}} \sum_{\boldsymbol{\mathbf{q}}, h} \mathfrak{N}_{\boldsymbol{\mathbf{q}},P}(h)\omega^\prime(\omega^{-1}(h)) \int_{\mathbb{R}^{|P|-1}} \widehat{f}(x_1, \ldots, x_{|P|-1}, -\boldsymbol{\mathbf{x}}\cdot \boldsymbol{\mathbf{1}}) \,d \boldsymbol{\mathbf{x}} (1+ o(1)). \]
Next, we may apply Euler's summation formula and a change of variables to conclude that
 \[ \mathcal{D}_N = \sum_{\mathcal{P}\in \mathscr{P}_m}\sum_{P \in \mathcal{P}} \bigg(\int_{\mathbb{R}^{|P|-1}} \widehat{f}(x_1, \ldots, x_{|P|-1}, -\boldsymbol{\mathbf{x}}\cdot \boldsymbol{\mathbf{1}})\,d \boldsymbol{\mathbf{x}} \bigg)(1+ o(1)). \]
\[ \mathcal{D}_N = \sum_{\mathcal{P}\in \mathscr{P}_m}\sum_{P \in \mathcal{P}} \bigg(\int_{\mathbb{R}^{|P|-1}} \widehat{f}(x_1, \ldots, x_{|P|-1}, -\boldsymbol{\mathbf{x}}\cdot \boldsymbol{\mathbf{1}})\,d \boldsymbol{\mathbf{x}} \bigg)(1+ o(1)). \]
From there we apply Fourier analysis as in [Reference Lutsko and TechnauLT21, Proof of Lemma 5.1] to conclude (5.1).
6. Bounding the off-diagonal
Recall that the off-diagonal contribution is given by
 \[ \mathcal{O}_N = \sum_{\boldsymbol{\mathbf{q}},\boldsymbol{\mathbf{u}}}\frac{1}{N^m}\sum_{\boldsymbol{\mathbf{r}},\boldsymbol{\mathbf{h}}} \eta(\boldsymbol{\mathbf{r}},\boldsymbol{\mathbf{h}})\int_0^1\frac{\mu_1\mu_2\cdots \mu_m}{r_1r_2\cdots r_m} \widehat{f}\bigg(\frac{\boldsymbol{\mathbf{\mu}}}{N}\bigg) \mathfrak{K}_{\boldsymbol{\mathbf{u}}}(\boldsymbol{\mathbf{\mu}}) \mathfrak{N}_{\boldsymbol{\mathbf{q}}}(\boldsymbol{\mathbf{\mu}},s)e(\Phi(\boldsymbol{\mathbf{h}},\boldsymbol{\mathbf{r}},s))\,{d}s, \]
\[ \mathcal{O}_N = \sum_{\boldsymbol{\mathbf{q}},\boldsymbol{\mathbf{u}}}\frac{1}{N^m}\sum_{\boldsymbol{\mathbf{r}},\boldsymbol{\mathbf{h}}} \eta(\boldsymbol{\mathbf{r}},\boldsymbol{\mathbf{h}})\int_0^1\frac{\mu_1\mu_2\cdots \mu_m}{r_1r_2\cdots r_m} \widehat{f}\bigg(\frac{\boldsymbol{\mathbf{\mu}}}{N}\bigg) \mathfrak{K}_{\boldsymbol{\mathbf{u}}}(\boldsymbol{\mathbf{\mu}}) \mathfrak{N}_{\boldsymbol{\mathbf{q}}}(\boldsymbol{\mathbf{\mu}},s)e(\Phi(\boldsymbol{\mathbf{h}},\boldsymbol{\mathbf{r}},s))\,{d}s, \]
where ![]() $r_i \asymp e^{u_i-q_i}q_i^{A-1}$ and the variable
$r_i \asymp e^{u_i-q_i}q_i^{A-1}$ and the variable ![]() $h_i \asymp q^{A}$. Finally, we have the phase function
$h_i \asymp q^{A}$. Finally, we have the phase function
 \[ \Phi(\boldsymbol{\mathbf{h}},\boldsymbol{\mathbf{r}},s) = -\sum_{i=1}^m r_i \exp((h_i-s)^{1/A}). \]
\[ \Phi(\boldsymbol{\mathbf{h}},\boldsymbol{\mathbf{r}},s) = -\sum_{i=1}^m r_i \exp((h_i-s)^{1/A}). \]
If we were to bound the oscillatory integral trivially, we would achieve the bound ![]() $\mathcal {O}_N \ll (\log N)^{(A+1)m}$. Therefore, all that is needed is a small power saving, for which we can exploit the oscillatory integral
$\mathcal {O}_N \ll (\log N)^{(A+1)m}$. Therefore, all that is needed is a small power saving, for which we can exploit the oscillatory integral
where
While bounding this integral is more involved in the present setting, we can nevertheless use the proof in [Reference Lutsko and TechnauLT21, § 6] as a guide. In Proposition 6.1 we achieve a power-saving; for this reason we can ignore the sums over ![]() $\boldsymbol {\mathbf {q}}$ and
$\boldsymbol {\mathbf {q}}$ and ![]() $\boldsymbol {\mathbf {u}}$ which give a logarithmic number of choices.
$\boldsymbol {\mathbf {u}}$ which give a logarithmic number of choices.
Since we are working on the off-diagonal we may write the phase as
 \begin{equation} \Phi(\boldsymbol{\mathbf{h}},\boldsymbol{\mathbf{r}},s) = \sum_{i=1}^l r_i \exp((h_i-s)^{1/A}) - \sum_{i=l}^L r_i \exp((h_i-s)^{1/A}), \end{equation}
\begin{equation} \Phi(\boldsymbol{\mathbf{h}},\boldsymbol{\mathbf{r}},s) = \sum_{i=1}^l r_i \exp((h_i-s)^{1/A}) - \sum_{i=l}^L r_i \exp((h_i-s)^{1/A}), \end{equation}
where we may now assume that ![]() $r_i >0$, the
$r_i >0$, the ![]() $h_i$ are pairwise distinct, and
$h_i$ are pairwise distinct, and ![]() $L< m$. We restrict attention to the case
$L< m$. We restrict attention to the case ![]() $L = m$ (this is also the most difficult case and the other cases can be done analogously).
$L = m$ (this is also the most difficult case and the other cases can be done analogously).
Proposition 6.1 Let ![]() $\Phi$ be as above. Then, for any
$\Phi$ be as above. Then, for any ![]() $\varepsilon >0$, we have
$\varepsilon >0$, we have
as ![]() $N \to \infty$, where
$N \to \infty$, where ![]() $\mu _{0,i} =\frac {r_i}{\omega ^\prime (\omega ^{-1}(h_i))}$. The implied constants are independent of
$\mu _{0,i} =\frac {r_i}{\omega ^\prime (\omega ^{-1}(h_i))}$. The implied constants are independent of ![]() $\boldsymbol {\mathbf {h}}$ and
$\boldsymbol {\mathbf {h}}$ and ![]() $\boldsymbol {\mathbf {r}}$ provided
$\boldsymbol {\mathbf {r}}$ provided ![]() $\eta _{\boldsymbol {\mathbf {r}}}(\boldsymbol {\mathbf {h}}) \neq 0$.
$\eta _{\boldsymbol {\mathbf {r}}}(\boldsymbol {\mathbf {h}}) \neq 0$.
Proof. As in [Reference Lutsko and TechnauLT21], we shall prove Proposition 6.1 by showing that one of the first ![]() $m$ derivatives of
$m$ derivatives of ![]() $\Phi$ is small. Then we can apply van der Corput's lemma to the integral and achieve the necessary bound. However, since the phase function is a sum of exponentials (as oppose to a sum of monomials as it was in our previous work), achieving these bounds is significantly more involved than in [Reference Lutsko and TechnauLT21].
$\Phi$ is small. Then we can apply van der Corput's lemma to the integral and achieve the necessary bound. However, since the phase function is a sum of exponentials (as oppose to a sum of monomials as it was in our previous work), achieving these bounds is significantly more involved than in [Reference Lutsko and TechnauLT21].
The ![]() $j$th derivative is given by (we will send
$j$th derivative is given by (we will send ![]() $s \mapsto -s$ to avoid having to deal with minus signs at the moment)
$s \mapsto -s$ to avoid having to deal with minus signs at the moment)
 \begin{align*} D_j &= \sum_{i=1}^m r_i \exp((h_i+s)^{1/A}) \\ &\quad \times\{A^{-j} (h_i+s)^{j/A-j} + c_{j,1}(h_i+s)^{(j-1)/A-j}+ \cdots + c_{j,j-1}(h_i+s)^{(1/A-j)}\}\\ &= : \sum_{i=1}^m b_i P_j(h_i) \end{align*}
\begin{align*} D_j &= \sum_{i=1}^m r_i \exp((h_i+s)^{1/A}) \\ &\quad \times\{A^{-j} (h_i+s)^{j/A-j} + c_{j,1}(h_i+s)^{(j-1)/A-j}+ \cdots + c_{j,j-1}(h_i+s)^{(1/A-j)}\}\\ &= : \sum_{i=1}^m b_i P_j(h_i) \end{align*}
where the ![]() $c_{j,k}$ depend only on
$c_{j,k}$ depend only on ![]() $A$ and
$A$ and ![]() $j$, where
$j$, where ![]() $b_i := r_i \exp ((h_i+s)^{1/A})$.
$b_i := r_i \exp ((h_i+s)^{1/A})$.
In matrix form, let ![]() $\boldsymbol {\mathbf {D}} :=(D_1, \ldots, D_m)$ denote the vector of the first
$\boldsymbol {\mathbf {D}} :=(D_1, \ldots, D_m)$ denote the vector of the first ![]() $m$ derivatives, and let
$m$ derivatives, and let ![]() $\boldsymbol {\mathbf {b}}:= (b_1, \ldots, b_m)$. Then
$\boldsymbol {\mathbf {b}}:= (b_1, \ldots, b_m)$. Then
To prove Proposition 6.1 we will lower-bound the determinant of ![]() $M$. Thus, we will show that
$M$. Thus, we will show that ![]() $M$ is invertible, and hence we will be able to lower-bound the
$M$ is invertible, and hence we will be able to lower-bound the ![]() $\ell ^2$-norm of
$\ell ^2$-norm of ![]() $\boldsymbol {\mathbf {D}}$. For this purpose, consider the
$\boldsymbol {\mathbf {D}}$. For this purpose, consider the ![]() $j$th row of
$j$th row of ![]() $M$,
$M$,
We can write ![]() $P_j(h_1) : = \sum _{k=0}^{j-1} c_{j,k} (h_i+s)^{t_k/A-j}$, where
$P_j(h_1) : = \sum _{k=0}^{j-1} c_{j,k} (h_i+s)^{t_k/A-j}$, where ![]() $t_k:= j-k$. Since the determinant is multilinear in the rows, we can decompose the determinant of
$t_k:= j-k$. Since the determinant is multilinear in the rows, we can decompose the determinant of ![]() $M$ as
$M$ as
where ![]() $c_{\boldsymbol {\mathbf {t}}}$ are constants depending only on
$c_{\boldsymbol {\mathbf {t}}}$ are constants depending only on ![]() $\boldsymbol {\mathbf {t}}$ and the sum over
$\boldsymbol {\mathbf {t}}$ and the sum over ![]() $\boldsymbol {\mathbf {t}}$ ranges over the set
$\boldsymbol {\mathbf {t}}$ ranges over the set
Let ![]() $X_{\boldsymbol {\mathbf {t}}}:= ((h_i+s)^{t_j/A-j})_{i,j\le m}$. We claim that
$X_{\boldsymbol {\mathbf {t}}}:= ((h_i+s)^{t_j/A-j})_{i,j\le m}$. We claim that ![]() $\det (M) = c_{\boldsymbol {\mathbf {t}}_M}\det (X_{\boldsymbol {\mathbf {t}}_M})(1+O(\max _i (h_i^{-1/A})))$ as
$\det (M) = c_{\boldsymbol {\mathbf {t}}_M}\det (X_{\boldsymbol {\mathbf {t}}_M})(1+O(\max _i (h_i^{-1/A})))$ as ![]() $N \to \infty$, where
$N \to \infty$, where ![]() $\boldsymbol {\mathbf {t}}_M := (1,2,\ldots, m)$.
$\boldsymbol {\mathbf {t}}_M := (1,2,\ldots, m)$.
To establish this claim, we appeal to the work of Khare and Tao; see Lemma 2.4. Namely, let ![]() $\boldsymbol {\mathbf {H}} := (h_1+s, \ldots, h_m +s)$ with
$\boldsymbol {\mathbf {H}} := (h_1+s, \ldots, h_m +s)$ with ![]() $h_1 > h_2> \cdots$ and let
$h_1 > h_2> \cdots$ and let ![]() $\boldsymbol {\mathbf {T}}(\boldsymbol {\mathbf {t}}):= (t_1/A-1, \ldots, t_m/A-m)$. Then we can write
$\boldsymbol {\mathbf {T}}(\boldsymbol {\mathbf {t}}):= (t_1/A-1, \ldots, t_m/A-m)$. Then we can write
Now invoking Lemma 2.4, we have
Note that we may need to interchange the rows and/or columns of ![]() $X_{\boldsymbol {\mathbf {t}}}$ to guarantee that the conditions of Lemma 2.4 are met. However, this will only change the sign of the determinant and thus will not affect the magnitude.
$X_{\boldsymbol {\mathbf {t}}}$ to guarantee that the conditions of Lemma 2.4 are met. However, this will only change the sign of the determinant and thus will not affect the magnitude.
Now, fix ![]() $\boldsymbol {\mathbf {t}} \in \mathcal {T}$ such that
$\boldsymbol {\mathbf {t}} \in \mathcal {T}$ such that ![]() $\boldsymbol {\mathbf {t}} \neq \boldsymbol {\mathbf {t}}_M$ and compare
$\boldsymbol {\mathbf {t}} \neq \boldsymbol {\mathbf {t}}_M$ and compare
Since ![]() $\boldsymbol {\mathbf {t}}_M \neq \boldsymbol {\mathbf {t}}$ we conclude that all coordinates
$\boldsymbol {\mathbf {t}}_M \neq \boldsymbol {\mathbf {t}}$ we conclude that all coordinates ![]() $t_i \le (\boldsymbol {\mathbf {t}}_M)_i$ and there exists a
$t_i \le (\boldsymbol {\mathbf {t}}_M)_i$ and there exists a ![]() $k$ such that
$k$ such that ![]() $t_k < (\boldsymbol {\mathbf {t}}_M)_k$. Therefore,
$t_k < (\boldsymbol {\mathbf {t}}_M)_k$. Therefore,
 \begin{align*} |\det(X_{\boldsymbol{\mathbf{t}}_M})| - |\det(X_{\boldsymbol{\mathbf{t}}})| &= |V(\boldsymbol{\mathbf{H}}) \boldsymbol{\mathbf{H}}^{\boldsymbol{\mathbf{T}}(\boldsymbol{\mathbf{t}}_M)-\boldsymbol{\mathbf{n}}_{\min}}|(1+ O(\max_i(h_i^{-1/A}))) \\ &= |\det(X_{\boldsymbol{\mathbf{t}}_M})|(1+ O(\max_i(h_i^{-1/A}))). \end{align*}
\begin{align*} |\det(X_{\boldsymbol{\mathbf{t}}_M})| - |\det(X_{\boldsymbol{\mathbf{t}}})| &= |V(\boldsymbol{\mathbf{H}}) \boldsymbol{\mathbf{H}}^{\boldsymbol{\mathbf{T}}(\boldsymbol{\mathbf{t}}_M)-\boldsymbol{\mathbf{n}}_{\min}}|(1+ O(\max_i(h_i^{-1/A}))) \\ &= |\det(X_{\boldsymbol{\mathbf{t}}_M})|(1+ O(\max_i(h_i^{-1/A}))). \end{align*}
This proves our claim.
Hence,
 \begin{align} |\det(M)| &= |c_{\boldsymbol{\mathbf{t}}_M} \det(X_{\boldsymbol{\mathbf{t}}_M})|(1+O(\max_i(h_i^{-1/A}))) \nonumber\\ &= |c_{\boldsymbol{\mathbf{t}}_M}V(\boldsymbol{\mathbf{H}}) \boldsymbol{\mathbf{H}}^{\boldsymbol{\mathbf{T}}(\boldsymbol{\mathbf{t}}_M)-\boldsymbol{\mathbf{n}}_{\min}}| (1+O(\max_i(h_i^{-1/A}))) \nonumber\\ &= |c_{\boldsymbol{\mathbf{t}}_M}|\bigg(\prod_{j=1}^m (h_j+s)^{j/A-2j+1}\bigg)\prod_{1\le i< j\le m} (h_i-h_j)(1+O(\max_i(h_i^{-1/A}))) \end{align}
\begin{align} |\det(M)| &= |c_{\boldsymbol{\mathbf{t}}_M} \det(X_{\boldsymbol{\mathbf{t}}_M})|(1+O(\max_i(h_i^{-1/A}))) \nonumber\\ &= |c_{\boldsymbol{\mathbf{t}}_M}V(\boldsymbol{\mathbf{H}}) \boldsymbol{\mathbf{H}}^{\boldsymbol{\mathbf{T}}(\boldsymbol{\mathbf{t}}_M)-\boldsymbol{\mathbf{n}}_{\min}}| (1+O(\max_i(h_i^{-1/A}))) \nonumber\\ &= |c_{\boldsymbol{\mathbf{t}}_M}|\bigg(\prod_{j=1}^m (h_j+s)^{j/A-2j+1}\bigg)\prod_{1\le i< j\le m} (h_i-h_j)(1+O(\max_i(h_i^{-1/A}))) \end{align}
which is clearly larger than ![]() $0$ (since
$0$ (since ![]() $h_i-h_j >1$ and
$h_i-h_j >1$ and ![]() $s>-1$).
$s>-1$).
Hence, ![]() $M$ is invertible, and we conclude that
$M$ is invertible, and we conclude that
 \begin{align*} \boldsymbol{\mathbf{D}} M^{-1} &= \boldsymbol{\mathbf{b}},\\ \|\boldsymbol{\mathbf{D}}\|_{2}\| M^{-1}\|_{\text{spec}} &\ge \|\boldsymbol{\mathbf{b}}\|_2,\\ \|\boldsymbol{\mathbf{D}}\|_{2} &\ge \frac{\|\boldsymbol{\mathbf{b}}\|_2}{\| M^{-1}\|_{\text{spec}}},\\ \end{align*}
\begin{align*} \boldsymbol{\mathbf{D}} M^{-1} &= \boldsymbol{\mathbf{b}},\\ \|\boldsymbol{\mathbf{D}}\|_{2}\| M^{-1}\|_{\text{spec}} &\ge \|\boldsymbol{\mathbf{b}}\|_2,\\ \|\boldsymbol{\mathbf{D}}\|_{2} &\ge \frac{\|\boldsymbol{\mathbf{b}}\|_2}{\| M^{-1}\|_{\text{spec}}},\\ \end{align*}
where ![]() $\|\cdot \|_{\text {spec}}$ denotes the spectral norm with respect to the
$\|\cdot \|_{\text {spec}}$ denotes the spectral norm with respect to the ![]() $\ell ^2$ vector norm. Recall that
$\ell ^2$ vector norm. Recall that ![]() $\|M^{-1}\|_{\text {spec}}$ is simply the largest eigenvalue of
$\|M^{-1}\|_{\text {spec}}$ is simply the largest eigenvalue of ![]() $M^{-1}$. Hence,
$M^{-1}$. Hence, ![]() $\det (M^{-1})^{1/m} \le \|M^{-1}\|_{\text {spec}}$.
$\det (M^{-1})^{1/m} \le \|M^{-1}\|_{\text {spec}}$.
We can bound the spectral norm by the maximum norm,
However, each entry of ![]() $M^{-1}$ is equal to
$M^{-1}$ is equal to ![]() $\frac {1}{\det (M)}$ times a cofactor of
$\frac {1}{\det (M)}$ times a cofactor of ![]() $M$, by Cramer's rule. This, together with the size of the
$M$, by Cramer's rule. This, together with the size of the ![]() $h_i$, is enough to show that
$h_i$, is enough to show that
Now using the bounds on ![]() $\boldsymbol {\mathbf {b}}$ (which come from the essential ranges of
$\boldsymbol {\mathbf {b}}$ (which come from the essential ranges of ![]() $h_i$ and
$h_i$ and ![]() $r_i$), we conclude that
$r_i$), we conclude that
From here we can apply the localized van der Corput's lemma [Reference Technau and YeshaTY20, Lemma 3.3] as we did in [Reference Lutsko and TechnauLT21] to conclude Proposition 6.1.
7. Proof of Lemma 3.1
Thanks to the preceding argument, we conclude that
Moreover, the off-diagonal term can be bounded using Proposition 6.1 as follows:
 \begin{align*} \mathcal{O}_N &= \frac{1}{N^m}\sum_{\boldsymbol{\mathbf{q}},\boldsymbol{\mathbf{u}}}\sum_{\boldsymbol{\mathbf{r}}, \boldsymbol{\mathbf{h}}} \eta(\boldsymbol{\mathbf{r,}},\boldsymbol{\mathbf{h}}) I(\boldsymbol{\mathbf{h}},\boldsymbol{\mathbf{r}})\\ &\ll \frac{1}{N^m}\sum_{\boldsymbol{\mathbf{q}},\boldsymbol{\mathbf{u}}}\sum_{\boldsymbol{\mathbf{r}}, \boldsymbol{\mathbf{h}}} \mathfrak{K}_{\boldsymbol{\mathbf{u}}}(\boldsymbol{\mathbf{\mu}}_0) \mathfrak{N}_{\boldsymbol{\mathbf{q}}}(\boldsymbol{\mathbf{\mu}}_0,0) \frac{e^{u_1 + \cdots + u_m}}{r_1 \cdots r_m} \max_{i \le m} e^{-u_i/m}N^{\varepsilon}. \end{align*}
\begin{align*} \mathcal{O}_N &= \frac{1}{N^m}\sum_{\boldsymbol{\mathbf{q}},\boldsymbol{\mathbf{u}}}\sum_{\boldsymbol{\mathbf{r}}, \boldsymbol{\mathbf{h}}} \eta(\boldsymbol{\mathbf{r,}},\boldsymbol{\mathbf{h}}) I(\boldsymbol{\mathbf{h}},\boldsymbol{\mathbf{r}})\\ &\ll \frac{1}{N^m}\sum_{\boldsymbol{\mathbf{q}},\boldsymbol{\mathbf{u}}}\sum_{\boldsymbol{\mathbf{r}}, \boldsymbol{\mathbf{h}}} \mathfrak{K}_{\boldsymbol{\mathbf{u}}}(\boldsymbol{\mathbf{\mu}}_0) \mathfrak{N}_{\boldsymbol{\mathbf{q}}}(\boldsymbol{\mathbf{\mu}}_0,0) \frac{e^{u_1 + \cdots + u_m}}{r_1 \cdots r_m} \max_{i \le m} e^{-u_i/m}N^{\varepsilon}. \end{align*}
Note that we are summing over reciprocals of ![]() $r_i$ and recall that the
$r_i$ and recall that the ![]() $h_i$ have size
$h_i$ have size ![]() $q_i^{A}$, so we may evaluate the sums over
$q_i^{A}$, so we may evaluate the sums over ![]() $\boldsymbol {\mathbf {h}}$ and
$\boldsymbol {\mathbf {h}}$ and ![]() $\boldsymbol {\mathbf {r}}$ and gain at most a logarithmic factor (which can be absorbed into the
$\boldsymbol {\mathbf {r}}$ and gain at most a logarithmic factor (which can be absorbed into the ![]() $\varepsilon$). Thus,
$\varepsilon$). Thus,
Likewise there are logarithmically many ![]() $\boldsymbol {\mathbf {q}}$ and
$\boldsymbol {\mathbf {q}}$ and ![]() $\boldsymbol {\mathbf {u}}$. Thus, maximizing the upper bound, we arrive at
$\boldsymbol {\mathbf {u}}$. Thus, maximizing the upper bound, we arrive at
This concludes our proof of Lemma 3.1. Hence, Theorem 1.3 follows from the argument in § 3.
8. Deducing Theorem 1.2 from Theorem 1.3
To see why Theorem 1.3 implies Theorem 1.2, we focus first in § 8.1 on the simplest case, ![]() $m=2$. The spirit of approximation argument therein works for any
$m=2$. The spirit of approximation argument therein works for any ![]() $m \ge 2$. However, because the notation gets more complicated when
$m \ge 2$. However, because the notation gets more complicated when ![]() $m\geq 3$, we present the general argument in § 8.2. In any case, the following lemma is at the core of the matter.
$m\geq 3$, we present the general argument in § 8.2. In any case, the following lemma is at the core of the matter.
Lemma 8.1 Let ![]() $f\in C^\infty _c(\mathbb {R})$ be positive. For any
$f\in C^\infty _c(\mathbb {R})$ be positive. For any ![]() $\varepsilon >0$, there exists a pointwise majorant
$\varepsilon >0$, there exists a pointwise majorant ![]() $F$ of
$F$ of ![]() $f$ with
$f$ with
A proof of this can be found in § 8.3.
8.1 The case  $m=2$
$m=2$
Suppose we knew that
Then, by the linearity of ![]() $f\mapsto R^{(2)}(N,f)$ and
$f\mapsto R^{(2)}(N,f)$ and ![]() $f\mapsto \int _\mathbb {R} f(x) \,d x$, the convergence of
$f\mapsto \int _\mathbb {R} f(x) \,d x$, the convergence of ![]() $R^{(2)}(N,f) \rightarrow {\mathbf {E}(f)}$ follows for all
$R^{(2)}(N,f) \rightarrow {\mathbf {E}(f)}$ follows for all ![]() $f\in C_c^\infty$. To verify (8.2) we show, for any positive
$f\in C_c^\infty$. To verify (8.2) we show, for any positive ![]() $f\in C_c^\infty$, that
$f\in C_c^\infty$, that
We first argue the estimate for the limit superior. Given ![]() $\varepsilon >0$, Lemma 8.1 guarantees that there exists a pointwise majorant
$\varepsilon >0$, Lemma 8.1 guarantees that there exists a pointwise majorant ![]() $F$ of
$F$ of ![]() $f$ satisfying (8.1). Observe that
$f$ satisfying (8.1). Observe that ![]() $R^{(2)}(N,f) - R^{(2)}(N,F)= R^{(2)}(N,f-F)$ and
$R^{(2)}(N,f) - R^{(2)}(N,F)= R^{(2)}(N,f-F)$ and ![]() $R^{(2)}(N,f-F)=-R^{(2)}(N,F-f)$. As a result,
$R^{(2)}(N,f-F)=-R^{(2)}(N,F-f)$. As a result,
Let ![]() $g:=F-f$. Combining (8.4), Theorem 1.3, and (8.1), we see that
$g:=F-f$. Combining (8.4), Theorem 1.3, and (8.1), we see that
Using Lemma 8.1, we find a pointwise majorant ![]() $G$ of
$G$ of ![]() $g$ with (8.1).
$g$ with (8.1).
Applying Theorem 1.3 once more,
By inserting this into (8.5) we obtain
for any choice of ![]() $\varepsilon >0$. Hence,
$\varepsilon >0$. Hence, ![]() $\limsup _{N\rightarrow \infty } R^{(2)}(N,f)\leq {\mathbf{E}(f)}$. Next, we show the right-hand side of (8.3). We notice that (8.4) and (8.6) yield
$\limsup _{N\rightarrow \infty } R^{(2)}(N,f)\leq {\mathbf{E}(f)}$. Next, we show the right-hand side of (8.3). We notice that (8.4) and (8.6) yield
Since ![]() $\varepsilon >0$ was arbitrary,
$\varepsilon >0$ was arbitrary, ![]() $\liminf _{N\rightarrow \infty } R^{(2)}(N,f)\geq {\mathbf {E}(f)}$ follows.
$\liminf _{N\rightarrow \infty } R^{(2)}(N,f)\geq {\mathbf {E}(f)}$ follows.
8.2 linearity-based  $m\geq 2$
$m\geq 2$
Let ![]() $f \in C_c^\infty (\mathbb {R}^{m-1})$ be positive, which we may assume by a linearity-based argument. Let
$f \in C_c^\infty (\mathbb {R}^{m-1})$ be positive, which we may assume by a linearity-based argument. Let ![]() $\varepsilon >0$. It suffices to demonstrate that
$\varepsilon >0$. It suffices to demonstrate that
Up to an error of at most ![]() $\varepsilon$, we can approximate
$\varepsilon$, we can approximate ![]() $f$ with respect to the supremum norm on
$f$ with respect to the supremum norm on ![]() $\mathbb {R}^{m-1}$ by a finite linear combination of functions
$\mathbb {R}^{m-1}$ by a finite linear combination of functions ![]() $\widetilde {f}$ each of which is the form
$\widetilde {f}$ each of which is the form ![]() $\widetilde {f}(\boldsymbol {\mathbf {x}}):=f_1(x_1)\cdots f_{m-1}(x_{m-1})$, where all
$\widetilde {f}(\boldsymbol {\mathbf {x}}):=f_1(x_1)\cdots f_{m-1}(x_{m-1})$, where all ![]() $f_i\in C_c^\infty (\mathbb {R})$. Thus, it suffices to establish (8.8) for
$f_i\in C_c^\infty (\mathbb {R})$. Thus, it suffices to establish (8.8) for ![]() $\widetilde {f}$ in place of
$\widetilde {f}$ in place of ![]() $f$. Given
$f$. Given ![]() $1\leq i< m$, Lemma 8.1 implies that there exists a pointwise majorant
$1\leq i< m$, Lemma 8.1 implies that there exists a pointwise majorant ![]() $F_i$ of
$F_i$ of ![]() $f_i$ satisfying (8.1). As a result,
$f_i$ satisfying (8.1). As a result, ![]() $F(\boldsymbol {\mathbf {x}}):= F_1(x_1)\cdots F_{m-1}(x_{m-1})$ is a pointwise majorant of
$F(\boldsymbol {\mathbf {x}}):= F_1(x_1)\cdots F_{m-1}(x_{m-1})$ is a pointwise majorant of ![]() $\widetilde {f}$. By using the identity
$\widetilde {f}$. By using the identity ![]() $ab-a'b'=a(b-b')+(a-a')b'$ inductively, we conclude that there exists a constant
$ab-a'b'=a(b-b')+(a-a')b'$ inductively, we conclude that there exists a constant ![]() $C_{\widetilde {f}}>0$ so that
$C_{\widetilde {f}}>0$ so that
no matter what our initial choice of the small parameter ![]() $\varepsilon$ was. Since
$\varepsilon$ was. Since ![]() $\widehat {F}(\boldsymbol {\mathbf {x}})=\widehat {F_1}(x_1)\cdots \widehat {F_{m-1}}(x_{m-1})$ is the product of compactly supported functions,
$\widehat {F}(\boldsymbol {\mathbf {x}})=\widehat {F_1}(x_1)\cdots \widehat {F_{m-1}}(x_{m-1})$ is the product of compactly supported functions, ![]() $\widehat {F}\in C_c^{\infty }(\mathbb {R}^{m-1})$. Notice that
$\widehat {F}\in C_c^{\infty }(\mathbb {R}^{m-1})$. Notice that
From here we reason exactly as we did in the case ![]() $m=2$ and thus we infer (8.8).
$m=2$ and thus we infer (8.8).
8.3 Proof of Lemma 8.1
The purpose of this subsection is to establish Lemma 8.1. We do so using arguments inspired by Marklof [Reference MarklofMar03, Section 8.6]. First, chose a ![]() $\delta >0$ small enough to ensure that
$\delta >0$ small enough to ensure that
Next, we perturb ![]() $f$ slightly by considering an auxiliary function
$f$ slightly by considering an auxiliary function ![]() $h$ defined via its Fourier transform
$h$ defined via its Fourier transform
The reason for working with this perturbation is to create the leeway needed to ensure that the final approximation ![]() $F$ is indeed positive. Let
$F$ is indeed positive. Let ![]() $\chi : \mathbb {R}\rightarrow [0,1]$ be an even, smooth function with
$\chi : \mathbb {R}\rightarrow [0,1]$ be an even, smooth function with ![]() $\operatorname {supp}(\chi )\subseteq [-2,2]$ and
$\operatorname {supp}(\chi )\subseteq [-2,2]$ and ![]() $\chi (x) = 1$ for
$\chi (x) = 1$ for ![]() $x \in [-1,1]$. We consider
$x \in [-1,1]$. We consider
and proceed to argue that there exists a cut-off ![]() $T>0$ so that
$T>0$ so that
for all ![]() $x\in \mathbb {R}$. Observe that (8.9) is trivially true at
$x\in \mathbb {R}$. Observe that (8.9) is trivially true at ![]() $x=0$. From now on let
$x=0$. From now on let ![]() $x\neq 0$. By using partial integration twice, we conclude
$x\neq 0$. By using partial integration twice, we conclude
 \begin{align*} \widehat{h_T}(x) - \widehat{h}(x) &= \int_{\mathbb{R}}\bigg[h(y) \chi\bigg(\frac{y}{T}\bigg)- h(y)\bigg] \bigg(\frac{d^2}{{{d}y}^2}\frac{e(-yx)}{(-2\pi i x)^2}\bigg)d y\\ &= \frac{1}{(-2\pi i x)^2}\int_{\mathbb{R}} \bigg(\frac{d^2}{{{d}y}^2}\bigg[h(y) \chi\bigg(\frac{y}{T}\bigg)- h(y)\bigg]\bigg) e(-yx) \,d y. \end{align*}
\begin{align*} \widehat{h_T}(x) - \widehat{h}(x) &= \int_{\mathbb{R}}\bigg[h(y) \chi\bigg(\frac{y}{T}\bigg)- h(y)\bigg] \bigg(\frac{d^2}{{{d}y}^2}\frac{e(-yx)}{(-2\pi i x)^2}\bigg)d y\\ &= \frac{1}{(-2\pi i x)^2}\int_{\mathbb{R}} \bigg(\frac{d^2}{{{d}y}^2}\bigg[h(y) \chi\bigg(\frac{y}{T}\bigg)- h(y)\bigg]\bigg) e(-yx) \,d y. \end{align*}
Furthermore,
Let ![]() $j\geq 0$ be an integer. To estimate the right-hand side of (8.10) efficiently, our next goal is to control the decay of the
$j\geq 0$ be an integer. To estimate the right-hand side of (8.10) efficiently, our next goal is to control the decay of the ![]() $j$th derivative of
$j$th derivative of ![]() $h$ uniformly. To this end, thanks to Fourier inversion, we see that
$h$ uniformly. To this end, thanks to Fourier inversion, we see that
Let ![]() $y\neq 0$. By using partial integration
$y\neq 0$. By using partial integration ![]() $t\geq j$ many times,
$t\geq j$ many times,
 \begin{align*} \vert h^{(j)}(y)\vert=\bigg\vert \int_{\mathbb{R}}\widehat{h}(\xi)(2\pi i \xi)^j \frac{d^t}{d\xi^t}\bigg(\frac{e(y\xi)}{(2\pi i y)^t}\bigg) d \xi\bigg\vert &\leq \frac{(2\pi)^{j}}{\vert 2\pi y\vert^{t}}\cdot \int_{\mathbb{R}}\bigg\vert \frac{d^t}{d\xi^t} (\xi^j \widehat{h}(\xi)) \bigg\vert d \xi\\ &\leq \frac{1}{\vert y\vert^{t}} \int_{\mathbb{R}}\bigg\vert\frac{d^t}{d\xi^t} \bigg(\xi^j f(\xi)+\frac{\delta \xi^j}{1+\xi^2}\bigg)\bigg\vert d \xi. \end{align*}
\begin{align*} \vert h^{(j)}(y)\vert=\bigg\vert \int_{\mathbb{R}}\widehat{h}(\xi)(2\pi i \xi)^j \frac{d^t}{d\xi^t}\bigg(\frac{e(y\xi)}{(2\pi i y)^t}\bigg) d \xi\bigg\vert &\leq \frac{(2\pi)^{j}}{\vert 2\pi y\vert^{t}}\cdot \int_{\mathbb{R}}\bigg\vert \frac{d^t}{d\xi^t} (\xi^j \widehat{h}(\xi)) \bigg\vert d \xi\\ &\leq \frac{1}{\vert y\vert^{t}} \int_{\mathbb{R}}\bigg\vert\frac{d^t}{d\xi^t} \bigg(\xi^j f(\xi)+\frac{\delta \xi^j}{1+\xi^2}\bigg)\bigg\vert d \xi. \end{align*}
By applying Leibniz's rule we conclude that, for any integers ![]() $t\geq j\geq 0$, there exists a constant
$t\geq j\geq 0$, there exists a constant ![]() $C(j,t,f)>0$ so that
$C(j,t,f)>0$ so that ![]() $\vert h^{(j)}(y)\vert \leq C(j,t,f)\vert y\vert ^{-t}$ for any
$\vert h^{(j)}(y)\vert \leq C(j,t,f)\vert y\vert ^{-t}$ for any ![]() $y\neq 0$. Taking this information in (8.10) into account yields
$y\neq 0$. Taking this information in (8.10) into account yields
whenever ![]() $y\neq 0$. Here the implied constants depend only on
$y\neq 0$. Here the implied constants depend only on ![]() $f$ and
$f$ and ![]() $\chi$. Because the left-hand side of (8.10) is supported on
$\chi$. Because the left-hand side of (8.10) is supported on ![]() $\vert y\vert \geq T$, it follows that
$\vert y\vert \geq T$, it follows that
Upon choosing ![]() $T$ large enough to overwhelm the implicit constant, we deduce that (8.9) holds true.
$T$ large enough to overwhelm the implicit constant, we deduce that (8.9) holds true.
Now put ![]() $F(x):=\widehat {h_T}(x)$. By the convolution theorem,
$F(x):=\widehat {h_T}(x)$. By the convolution theorem, ![]() $F(x)=\int _\mathbb {R} \widehat {h}(x-y) \widehat {\chi }(y) \,d y$. Notice that
$F(x)=\int _\mathbb {R} \widehat {h}(x-y) \widehat {\chi }(y) \,d y$. Notice that ![]() $\widehat {h}$ and
$\widehat {h}$ and ![]() $\widehat {\chi }$ are real-valued (the latter being the Fourier transform of an even, real-valued function). Therefore,
$\widehat {\chi }$ are real-valued (the latter being the Fourier transform of an even, real-valued function). Therefore, ![]() $F$ is real-valued. To proceed, we notice that the triangle inequality implies
$F$ is real-valued. To proceed, we notice that the triangle inequality implies
Hence, ![]() $F$ is a pointwise majorant of
$F$ is a pointwise majorant of ![]() $f$ and, in particular, positive. Furthermore,
$f$ and, in particular, positive. Furthermore,
Appendix A. A sublacunary partition of unity
Choose large integers ![]() $N,Q\geq 10$, with
$N,Q\geq 10$, with ![]() $e^{Q}\leq N< e^{Q+1}$. In this section we justify that the functions
$e^{Q}\leq N< e^{Q+1}$. In this section we justify that the functions ![]() $\mathfrak {N}_q$, where
$\mathfrak {N}_q$, where ![]() $0\leq q \leq 2Q-1$, from § 3.2 exist. We assume in the following that
$0\leq q \leq 2Q-1$, from § 3.2 exist. We assume in the following that ![]() $Q$ is an odd integer. The case that
$Q$ is an odd integer. The case that ![]() $Q$ is even can be handled very similarly. We start from the disjoint decomposition
$Q$ is even can be handled very similarly. We start from the disjoint decomposition
To construct a suitable partition of unity for the first and the second set we require somewhat different treatment. However, the main idea is rather simple, and the mechanics are the same for both. We begin with the former. We cut ![]() $[1,e^{Q-1})$ into a union of the dyadic intervals
$[1,e^{Q-1})$ into a union of the dyadic intervals ![]() $[e^{q},e^{q+1})$. Then we smooth out the corners of their indicator functions in the following way. We smooth every second indicator function (changing their support only marginally), and adjust the remaining ones so that neighboring functions always sum to
$[e^{q},e^{q+1})$. Then we smooth out the corners of their indicator functions in the following way. We smooth every second indicator function (changing their support only marginally), and adjust the remaining ones so that neighboring functions always sum to ![]() $1$. Furthermore, to decompose
$1$. Furthermore, to decompose ![]() $[e^{Q-1},N]$ in a sublacunary manner, we use a similar strategy. This time we cut the interval into a union of sublacunary intervals, smoothing the ones with odd indices and then adjusting the corners of the even ones appropriately.
$[e^{Q-1},N]$ in a sublacunary manner, we use a similar strategy. This time we cut the interval into a union of sublacunary intervals, smoothing the ones with odd indices and then adjusting the corners of the even ones appropriately.
To execute this plan, fix a smooth function ![]() $\beta : \mathbb {R}\rightarrow \mathbb {R}_{\geq 0}$ which is supported in a compact interval. For example,
$\beta : \mathbb {R}\rightarrow \mathbb {R}_{\geq 0}$ which is supported in a compact interval. For example,
 \[ \beta (x):=\begin{cases} \exp\bigg(-\dfrac{1}{1-\vert x \vert^2}\bigg) & \mathrm{for}\ 0\leq\vert x\vert<1,\\ 0 & \mathrm{otherwise} \end{cases} \]
\[ \beta (x):=\begin{cases} \exp\bigg(-\dfrac{1}{1-\vert x \vert^2}\bigg) & \mathrm{for}\ 0\leq\vert x\vert<1,\\ 0 & \mathrm{otherwise} \end{cases} \]
is a viable choice. By translating (if need be) and scaling, we modify ![]() $\beta$ to obtain a function
$\beta$ to obtain a function ![]() $B: \mathbb {R}\rightarrow \mathbb {R}_{\geq 0}$ which is smooth, supported in
$B: \mathbb {R}\rightarrow \mathbb {R}_{\geq 0}$ which is smooth, supported in ![]() $[-1/100, 1/100]$, and
$[-1/100, 1/100]$, and ![]() $L^1$-normalized, that is,
$L^1$-normalized, that is,
Denote the convolution of functions ![]() $g_1,g_2: \mathbb {R}\rightarrow \mathbb {R}$ by
$g_1,g_2: \mathbb {R}\rightarrow \mathbb {R}$ by
Clearly, if ![]() $g_1$ is
$g_1$ is ![]() $j$ times continuously differentiable, then
$j$ times continuously differentiable, then ![]() $g_1*g_2$ is
$g_1*g_2$ is ![]() $j$ times continuously differentiable and
$j$ times continuously differentiable and
A.1 The regime  $0\leq q< Q$
$0\leq q< Q$
Denote the indicator function of an interval ![]() $I$ by
$I$ by ![]() $\mathbf {1}_{I}$. The smooth function
$\mathbf {1}_{I}$. The smooth function ![]() $B_{y}(x):=e^{-{y}} B(e^{-y}x)$ is important in what follows, noting in particular that it is supported in the interval
$B_{y}(x):=e^{-{y}} B(e^{-y}x)$ is important in what follows, noting in particular that it is supported in the interval ![]() $[-e^{y}/100,e^{y}/100]$. For even index
$[-e^{y}/100,e^{y}/100]$. For even index ![]() $q=2t \in \{0,\ldots,Q-1\}$, we let
$q=2t \in \{0,\ldots,Q-1\}$, we let
These functions inherit the smoothness of ![]() $B$. By (A.1), we have
$B$. By (A.1), we have
for each integer ![]() $j\geq 0$. (The implied constant is allowed to depend on the choice of
$j\geq 0$. (The implied constant is allowed to depend on the choice of ![]() $B$, which, however, is fixed throughout and therefore this dependency is suppressed.) Next, for every odd index
$B$, which, however, is fixed throughout and therefore this dependency is suppressed.) Next, for every odd index ![]() $q=2t+1 \in \{0,\ldots,Q-1\}$ we define
$q=2t+1 \in \{0,\ldots,Q-1\}$ we define
 \[ \mathfrak{N}_{2t+1}(x):= \begin{cases} 0, & \mathrm{if}\ x <0.98 \cdot e^{2t},\\ 1-\mathfrak{N}_{2t}(x), & \mathrm{if}\ 0.98 \cdot e^{2t}\leq x< 1.02 \cdot e^{2t},\\ 1, & \mathrm{if}\ 1.02 \cdot e^{2t}\leq x < 0.98 \cdot e^{2t+2},\\ 1-\mathfrak{N}_{2t+2}(x), & \mathrm{if}\ 0.98 \cdot e^{2t+2} \leq x < 1.02 \cdot e^{2t+2},\\ 0, & \mathrm{if}\ e^{2t+2}\leq x. \end{cases} \]
\[ \mathfrak{N}_{2t+1}(x):= \begin{cases} 0, & \mathrm{if}\ x <0.98 \cdot e^{2t},\\ 1-\mathfrak{N}_{2t}(x), & \mathrm{if}\ 0.98 \cdot e^{2t}\leq x< 1.02 \cdot e^{2t},\\ 1, & \mathrm{if}\ 1.02 \cdot e^{2t}\leq x < 0.98 \cdot e^{2t+2},\\ 1-\mathfrak{N}_{2t+2}(x), & \mathrm{if}\ 0.98 \cdot e^{2t+2} \leq x < 1.02 \cdot e^{2t+2},\\ 0, & \mathrm{if}\ e^{2t+2}\leq x. \end{cases} \]
Since ![]() $\mathfrak {N}_{2t+1}$ is given piecewise by concatenating five smooth functions, we can infer that
$\mathfrak {N}_{2t+1}$ is given piecewise by concatenating five smooth functions, we can infer that ![]() $\mathfrak {N}_{2t+1}$ is a smooth function as soon as we establish that the four relevant boundary points do not cause issues. A quick inspection reveals that
$\mathfrak {N}_{2t+1}$ is a smooth function as soon as we establish that the four relevant boundary points do not cause issues. A quick inspection reveals that ![]() $\mathfrak {N}_{q}$, for any
$\mathfrak {N}_{q}$, for any ![]() $q< Q$, is supported in
$q< Q$, is supported in ![]() $[0.98 \cdot e^{q}, 1.02 \cdot e^{q+1}] \subseteq [e^q/2,3 e^q)$. Hence,
$[0.98 \cdot e^{q}, 1.02 \cdot e^{q+1}] \subseteq [e^q/2,3 e^q)$. Hence, ![]() $\mathfrak {N}_{2t+1}$ is smooth. Furthermore,
$\mathfrak {N}_{2t+1}$ is smooth. Furthermore, ![]() $\mathfrak {N}_{2t+1}$ is monotonically increasing (though not always strictly) on the interval
$\mathfrak {N}_{2t+1}$ is monotonically increasing (though not always strictly) on the interval ![]() $[0.98 \cdot e^{q}, 1.02 \cdot e^{q}]$, equal to
$[0.98 \cdot e^{q}, 1.02 \cdot e^{q}]$, equal to ![]() $1$ on
$1$ on ![]() $[1.02 \cdot e^{q}, 0.98\cdot e^{q+1}]$, and monotonically decreasing (not always strictly) on
$[1.02 \cdot e^{q}, 0.98\cdot e^{q+1}]$, and monotonically decreasing (not always strictly) on ![]() $[0.98 \cdot e^{q+1}, 1.02\cdot e^{q+1}]$. The function
$[0.98 \cdot e^{q+1}, 1.02\cdot e^{q+1}]$. The function ![]() $\mathfrak {N}_{2t}$ has analogous monotonicity properties. Hence,
$\mathfrak {N}_{2t}$ has analogous monotonicity properties. Hence, ![]() $\mathfrak {N}_{q}'$ also has exactly one sign change. By construction,
$\mathfrak {N}_{q}'$ also has exactly one sign change. By construction,
whenever ![]() $e^q \leq x \leq e^{q+1}$, irrespective of the parity of
$e^q \leq x \leq e^{q+1}$, irrespective of the parity of ![]() $q$. Moreover, (A.2) implies that
$q$. Moreover, (A.2) implies that
Consequently, the family of functions ![]() $\{ \mathfrak {N}_{q}: 0\leq q < Q\}$ satisfies (3.7).
$\{ \mathfrak {N}_{q}: 0\leq q < Q\}$ satisfies (3.7).
A.2 The regime  $Q\leq q<2Q$
$Q\leq q<2Q$
Put ![]() $\mathcal {Q}:= 2.8 \cdot e^{Q}/Q$. To render the subsequent formulas more transparent, define
$\mathcal {Q}:= 2.8 \cdot e^{Q}/Q$. To render the subsequent formulas more transparent, define ![]() $a_t:=e^{Q} +(t-1/2) \mathcal {Q}$. Observe that
$a_t:=e^{Q} +(t-1/2) \mathcal {Q}$. Observe that
and where ![]() $T$ is the unique integer such that
$T$ is the unique integer such that ![]() $N \in \mathcal {I}_{T}$. In fact, due to the fact that
$N \in \mathcal {I}_{T}$. In fact, due to the fact that ![]() $e/2.8<0.971$, we see that
$e/2.8<0.971$, we see that ![]() $0\leq T \leq 0.98 Q$. Informally, our next step is to again smooth out every other partition interval in the aforementioned cover. However, this time we need to be mindful at the end points of the partition which, necessarily, play a distinguished role. The end points will be handled at the end of this paragraph, and we first deal with the bulk of the intervals. Writing any even index
$0\leq T \leq 0.98 Q$. Informally, our next step is to again smooth out every other partition interval in the aforementioned cover. However, this time we need to be mindful at the end points of the partition which, necessarily, play a distinguished role. The end points will be handled at the end of this paragraph, and we first deal with the bulk of the intervals. Writing any even index ![]() $q\in \{Q+1,Q+T+1\}$ in the form
$q\in \{Q+1,Q+T+1\}$ in the form ![]() $q=Q+2t+1$, with
$q=Q+2t+1$, with ![]() $0\leq t \leq T$, we define
$0\leq t \leq T$, we define
Next, writing any odd index ![]() $q\in \{Q+2,Q+T+1\}$ in the form
$q\in \{Q+2,Q+T+1\}$ in the form ![]() $q=Q+2t$, with
$q=Q+2t$, with ![]() $1\leq t \leq T$, we put
$1\leq t \leq T$, we put
 \[ \mathfrak{N}_{Q+2t}(x):= \begin{cases} 0, & \mathrm{if}\ x < a_{2t-2} - 0.02\cdot \mathcal{Q},\\ 1-\mathfrak{N}_{Q+2t-2}(x), & \mathrm{if}\ a_{2t-2} - 0.02\cdot \mathcal{Q} \leq x< a_{2t-2} + 0.02\cdot \mathcal{Q},\\ 1, & \mathrm{if}\ a_{2t-2} + 0.02\cdot \mathcal{Q} \leq x < a_{2t+2} - 0.02\cdot \mathcal{Q},\\ 1-\mathfrak{N}_{Q+2t+2}(x) & \mathrm{if}\ a_{2t+2} - 0.02\cdot \mathcal{Q} \leq x < a_{2t+2} + 0.02\cdot \mathcal{Q},\\ 0, & \mathrm{if}\ a_{2t+2} + 0.02\cdot \mathcal{Q}\leq x. \end{cases} \]
\[ \mathfrak{N}_{Q+2t}(x):= \begin{cases} 0, & \mathrm{if}\ x < a_{2t-2} - 0.02\cdot \mathcal{Q},\\ 1-\mathfrak{N}_{Q+2t-2}(x), & \mathrm{if}\ a_{2t-2} - 0.02\cdot \mathcal{Q} \leq x< a_{2t-2} + 0.02\cdot \mathcal{Q},\\ 1, & \mathrm{if}\ a_{2t-2} + 0.02\cdot \mathcal{Q} \leq x < a_{2t+2} - 0.02\cdot \mathcal{Q},\\ 1-\mathfrak{N}_{Q+2t+2}(x) & \mathrm{if}\ a_{2t+2} - 0.02\cdot \mathcal{Q} \leq x < a_{2t+2} + 0.02\cdot \mathcal{Q},\\ 0, & \mathrm{if}\ a_{2t+2} + 0.02\cdot \mathcal{Q}\leq x. \end{cases} \]
The function ![]() $\mathfrak {N}_{Q}$ plays a distinguished role as it is the final partition element and of a different scale of unity given provided by the functions
$\mathfrak {N}_{Q}$ plays a distinguished role as it is the final partition element and of a different scale of unity given provided by the functions ![]() $\{\mathfrak {N}_{q}:0\leq q< Q\}$ and the sublacunary one furnished by
$\{\mathfrak {N}_{q}:0\leq q< Q\}$ and the sublacunary one furnished by ![]() $\{\mathfrak {N}_{q}:Q< q<2Q-1\}$. To smoothly link these two, we let
$\{\mathfrak {N}_{q}:Q< q<2Q-1\}$. To smoothly link these two, we let
 \[ \mathfrak{N}_{Q}(x):= \begin{cases} 0, & \mathrm{if}\ x < 0.98 e^{Q},\\ 1-\mathfrak{N}_{Q-1}(x), & \mathrm{if}\ 0.98 e^{Q} \leq x< 0.98 e^{Q},\\ 1, & \mathrm{if}\ a_{2t-1} + 00.2\cdot \mathcal{Q} \leq x < a_{2t+1} - 00.2\cdot \mathcal{Q},\\ 1-\mathfrak{N}_{Q+1}(x) & \mathrm{if}\ a_{2t+1} - 00.2\cdot \mathcal{Q} \leq x < a_{2t+1} + 00.2\cdot \mathcal{Q},\\ 0, & \mathrm{if}\ a_{2t+1} + 00.2\cdot \mathcal{Q}\leq x. \end{cases} \]
\[ \mathfrak{N}_{Q}(x):= \begin{cases} 0, & \mathrm{if}\ x < 0.98 e^{Q},\\ 1-\mathfrak{N}_{Q-1}(x), & \mathrm{if}\ 0.98 e^{Q} \leq x< 0.98 e^{Q},\\ 1, & \mathrm{if}\ a_{2t-1} + 00.2\cdot \mathcal{Q} \leq x < a_{2t+1} - 00.2\cdot \mathcal{Q},\\ 1-\mathfrak{N}_{Q+1}(x) & \mathrm{if}\ a_{2t+1} - 00.2\cdot \mathcal{Q} \leq x < a_{2t+1} + 00.2\cdot \mathcal{Q},\\ 0, & \mathrm{if}\ a_{2t+1} + 00.2\cdot \mathcal{Q}\leq x. \end{cases} \]
To formally complete the construction, we put
By arguing very much as in the regime ![]() $0\leq q< Q$, one can check that
$0\leq q< Q$, one can check that ![]() $\{ \mathfrak {N}_{q}: Q\leq q <2Q\}$ has the required properties and, in particular, is such that (3.7) holds true.
$\{ \mathfrak {N}_{q}: Q\leq q <2Q\}$ has the required properties and, in particular, is such that (3.7) holds true.
Acknowledgements
We thank Apoorva Khare, Jens Marklof and Zeev Rudnick for comments on a previous version of the paper. Furthermore, we are grateful to the anonymous referee for a careful reading and comments that helped remove inaccuracies from an earlier version of the paper.
Conflicts of interest
None.
Financial support
NT was supported by a Schrödinger Fellowship of the Austrian Science Fund (FWF): project J 4464-N.
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.