Hostname: page-component-6bf8c574d5-b4m5d Total loading time: 0 Render date: 2025-02-19T21:30:45.788Z Has data issue: false hasContentIssue false
  • English
  • Français

From ALE to ALF gravitational instantons

Part of: Global differential geometry

Published online by Cambridge University Press:  03 May 2018

Hugues Auvray
Hugues Auvray*
Affiliation:
Laboratoire de Mathématiques d’Orsay, Université Paris-Sud, CNRS, Université Paris-Saclay, 91405 Orsay, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we give an analytic construction of ALF hyperkähler metrics on smooth deformations of the Kleinian singularity 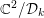$\mathbb{C}^{2}/{\mathcal{D}}_{k}$, with 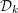${\mathcal{D}}_{k}$ the binary dihedral group of order 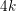$4k$, 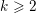$k\geqslant 2$. More precisely, we start from the ALE hyperkähler metrics constructed on these spaces by Kronheimer, and use analytic methods, e.g. resolution of a Monge–Ampère equation, to produce ALF hyperkähler metrics with the same associated Kähler classes.

Keywords

gravitational instantonsMonge–Ampère equation

MSC classification

Primary: 53C20: Global Riemannian geometry, including pinching 53C21: Methods of Riemannian geometry, including PDE methods; curvature restrictions 53C26: Hyper-Kähler and quaternionic Kähler geometry, “special” geometry
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 6 , June 2018 , pp. 1159 - 1221
Copyright
© The Author 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atiyah, M. and Hitchin, N., The geometry and dynamics of magnetic monopoles, M. B. Porter Lectures (Princeton University Press, Princeton, NJ, 1988).CrossRefGoogle Scholar
Bamler, R., Stability of Einstein metrics of negative curvature, PhD thesis, Princeton University (ProQuest LLC, Ann Arbor, MI, 2011).Google Scholar
Bando, S., Kasue, A. and Nakajima, H., On a construction of coordinates at infinity on manifolds with fast curvature decay and maximal volume growth , Invent. Math. 97 (1989), 313–349.CrossRefGoogle Scholar
Besse, A. L., Einstein manifolds, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 10 (Springer, Berlin, 1987).CrossRefGoogle Scholar
Biquard, O., Differential geometry and global analysis, Lecture Notes available athttp://www.math.ens.fr/ biquard/dgga2007.pdf.Google Scholar
Biquard, O. and Minerbe, V., A Kummer construction for gravitational instantons , Comm. Math. Phys. 308 (2011), 773–794.CrossRefGoogle Scholar
Biquard, O. and Rollin, Y., Smoothing singular extremal Kähler surfaces and minimal Lagrangians, Preprint (2012), arXiv:1211.6957 [math.DG].Google Scholar
Buser, P. and Karcher, H., Gromov’s almost flat manifolds, Astérisque, vol. 81 (Société Mathématique de France, Paris, 1981).Google Scholar
Chen, G. and Chen, X., Gravitational instantons with faster than quadratic decay (I), Preprint (2015), arXiv:1505.01790v1 [math.DG].Google Scholar
Chen, G. and Chen, X., Gravitational instantons with faster than quadratic decay (II), Preprint (2015), arXiv:1508.07908v2 [math.DG].Google Scholar
Cherkis, S. and Hitchin, N., Gravitational instantons of type D k , Comm. Math. Phys. 260 (2005), 299–317.CrossRefGoogle Scholar
Cherkis, S. and Kapustin, A., D k gravitational instantons and Nahm equations , Adv. Theor. Math. Phys. 2 (1998), 1287–1306.CrossRefGoogle Scholar
Cherkis, S. and Kapustin, A., Singular monopoles and gravitational instantons , Comm. Math. Phys. 203 (1999), 713–728.CrossRefGoogle Scholar
Dancer, A. S., A family of hyper-Kähler manifolds , Quart. J. Math. Oxford Ser. (2) 45 (1994), 463–478.CrossRefGoogle Scholar
Eguchi, T., Gilkey, P. B. and Hanson, A. J., Gravitation, gauge theories and differential geometry , Phys. Rep. 66 (1980), 213–393.CrossRefGoogle Scholar
Foscolo, L., ALF gravitational instantons and collapsing Ricci-flat metrics on the K3 surface, J. Differential Geom., to appear. Preprint (2016), arXiv:1603.06315 [math.DG].Google Scholar
Gibbons, G. W. and Hawking, S. W., Gravitational multi-instantons , Phys. Lett. B 78 (1976), 430–432.CrossRefGoogle Scholar
Gromov, M., Metric structures for Riemannian and non-Riemannian spaces, Progress in Mathematics, vol. 152 (Birkhäuser, Boston, MA, 1999); With appendices by M. Katz, P. Pansu and S. Semmes. Translated from the French by Sean Michael Bates.Google Scholar
Gursky, M. and Viaclovsky, J. A., Critical metrics on connected sums of Einstein four-manifolds , Adv. Math. 292 (2016), 210–315.CrossRefGoogle Scholar
Hawking, S. W., Gravitational instantons , Phys. Lett. A 60 (1977), 81–83.CrossRefGoogle Scholar
Hein, H. J., On gravitational instantons, PhD thesis, Princeton University, 2010.Google Scholar
Hein, H. J. and Conlon, R. J., Asymptotically conical Calabi–Yau manifolds, I , Duke Math. J. 162 (2013), 2855–2902.Google Scholar
Hitchin, N. J., Twistor construction of Einstein metrics, Global Riemannian Geometry (Durham, 1983), Ellis Horwood Series in Mathematics and Its Applications (Ellis Horwood, Chichester, 1984), 115–125.Google Scholar
Joyce, D., Compact manifolds with special holonomy, Oxford Mathematical Monographs (Oxford University Press, Oxford, 2000).CrossRefGoogle Scholar
Kronheimer, P. B., The construction of ALE spaces as hyper-Kähler quotients , J. Differential Geom. 29 (1989), 665–683.CrossRefGoogle Scholar
Kronheimer, P. B., A Torelli-type theorem for gravitational instantons , J. Differential Geom. 29 (1989), 685–697.CrossRefGoogle Scholar
LeBrun, C., Complete Ricci-flat Kähler metrics on ℂ n need not be flat , Proc. Sympos. Pure Math. 52.2 (1991), 297–304.CrossRefGoogle Scholar
Li, C., On sharp rates and analytic compactifications of asymptotically conical Kähler metrics, Preprint (2014), arXiv:1405.2433v4 [math.DG].Google Scholar
McKay, J., Graphs, singularities, and finite groups , in The santa cruz conference on finite groups (University of California, Santa Cruz, CA, 1979), Proceedings of Symposia in Pure Mathematics, vol. 37 (American Mathematical Society, Providence, RI, 1980), 183–186.Google Scholar
Minerbe, V., Sur l’effondrement à l’infini des variétés asymptotiquement plates, PhD thesis, Université de Nantes (2007), available athttps://webusers.imj-prg.fr/uploads//vincent.minerbe/Articles/theseminerbe.pdf.Google Scholar
Minerbe, V., A mass for ALF manifolds , Comm. Math. Phys. 289 (2009), 925–955.CrossRefGoogle Scholar
Minerbe, V., Rigidity for Multi-Taub-NUT metrics , J. Reine Angew. Math. 656 (2011), 47–58.Google Scholar
Page, D. N., A periodic but nonstationary gravitational instanton , Phys. Lett. B 100 (1981), 313–315.CrossRefGoogle Scholar
Saloff-Coste, L., Uniformly elliptic operators on Riemannian manifolds , J. Differential Geom. 36 (1992), 417–450.CrossRefGoogle Scholar
Şuvaina, I., ALE Ricci-flat Kähler metrics and deformations of quotient surface singularities , Ann. Global Anal. Geom. 41 (2012), 109–123.CrossRefGoogle Scholar
Tian, G. and Yau, S. T., Complete Kähler manifolds with zero Ricci curvature. I , J. Amer. Math. Soc. 3 (1990), 579–609.Google Scholar
Tian, G. and Yau, S. T., Complete Kähler manifolds with zero Ricci curvature. II , Invent. Math. 106 (1991), 27–60.CrossRefGoogle Scholar
Wright, D., Compact anti-self-dual orbifolds with torus actions , Selecta Math. (N.S.) 17 (2011), 223–280.CrossRefGoogle Scholar
Yau, S. T., On the Ricci curvature of a compact Kähler manifold and the complex Monge–Ampère equation, I ∗ , Comm. Pure Appl. Math. 31 (1978), 339–441.CrossRefGoogle Scholar