Let ϕ be a Drinfeld module of rank 2 over the field of rational functions , with 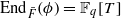. Let K be a fixed imaginary quadratic field over F and d a positive integer. For each prime 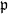of good reduction for ϕ, let 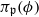be a root of the characteristic polynomial of the Frobenius endomorphism of ϕ over the finite field 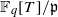. Let Πϕ(K;d) be the number of primes 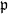of degree d such that the field extension 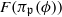is the fixed imaginary quadratic field K. We present upper bounds for Πϕ(K;d) obtained by two different approaches, inspired by similar ones for elliptic curves. The first approach, inspired by the work of Serre, is to consider the image of Frobenius in a mixed Galois representation associated to K and to the Drinfeld module ϕ. The second approach, inspired by the work of Cojocaru, Fouvry and Murty, is based on an application of the square sieve. The bounds obtained with the first method are better, but depend on the fixed quadratic imaginary field K. In our application of the second approach, we improve the results of Cojocaru, Murty and Fouvry by considering projective Galois representations.