Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-11T17:44:03.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Foundations of Boij–Söderberg theory for Grassmannians

Part of: Commutative algebra: Homological methods (Co)homology theory Combinatorics Algebraic combinatorics

Published online by Cambridge University Press:  11 September 2018

Nicolas Ford  and
Jake Levinson
Nicolas Ford
Affiliation:
Mathematics Department, University of California, Berkeley, USA email [email protected]
Jake Levinson
Affiliation:
Mathematics Department, University of Michigan, Ann Arbor, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Boij–Söderberg theory characterizes syzygies of graded modules and sheaves on projective space. This paper continues earlier work with Sam, extending the theory to the setting of 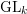$\text{GL}_{k}$-equivariant modules and sheaves on Grassmannians. Algebraically, we study modules over a polynomial ring in 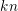$kn$ variables, thought of as the entries of a 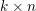$k\times n$ matrix. We give equivariant analogs of two important features of the ordinary theory: the Herzog–Kühl equations and the pairing between Betti and cohomology tables. As a necessary step, we also extend previous results, concerning the base case of square matrices, to cover complexes other than free resolutions. Our statements specialize to those of ordinary Boij–Söderberg theory when 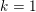$k=1$. Our proof of the equivariant pairing gives a new proof in the graded setting: it relies on finding perfect matchings on certain graphs associated to Betti tables and to spectral sequences. As an application, we construct three families of extremal rays on the Betti cone for 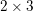$2\times 3$ matrices.

Keywords

Boij–Söderberg theorysyzygiesGrassmannians

MSC classification

Primary: 13D02: Syzygies, resolutions, complexes
Secondary: 14F05: Sheaves, derived categories of sheaves and related constructions 05E10: Combinatorial aspects of representation theory 05A15: Exact enumeration problems, generating functions
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 10 , October 2018 , pp. 2205 - 2238
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Current address: Mathematics Department, University of Washington, Seattle, WA, USA

The second author was supported by a Rackham Predoctoral Fellowship and by NSERC grant PDF-502633.

References

Berkesch, C., Burke, J., Erman, D. and Gibbons, C., The cone of Betti diagrams over a hypersurface ring of low embedding dimension , J. Pure Appl. Algebra 216 (2012), 2256–2268; MR 2925819.Google Scholar
Berkesch Zamaere, C., Erman, D., Kummini, M. and Sam, S. V., Tensor complexes: multilinear free resolutions constructed from higher tensors , J. Eur. Math. Soc. (JEMS) 15 (2013), 2257–2295; MR 3120743.Google Scholar
Berkesch Zamaere, C., Erman, D. and Smith, G. G., Virtual resolutions for a product of projective spaces, Preprint (2017), arXiv:1703.07631.Google Scholar
Boij, M. and Söderberg, J., Graded Betti numbers of Cohen–Macaulay modules and the multiplicity conjecture , J. Lond. Math. Soc. (2) 78 (2008), 85–106; MR 2427053.Google Scholar
Buch, A. S., A Littlewood-Richardson rule for the K-theory of Grassmannians , Acta Math. 189 (2002), 37–78; MR 1946917.Google Scholar
Chapalkatti, J., A generalization of Castelnuovo regularity to Grassmann manifolds, PhD thesis, Purdue University (1999).Google Scholar
Eisenbud, D., Erman, D. and Schreyer, F.-O., Filtering free resolutions , Compos. Math. 149 (2013), 754–772; MR 3069361.Google Scholar
Eisenbud, D. and Erman, D., Categorified duality in Boij–Söderberg theory and invariants of free complexes , J. Eur. Math. Soc. (JEMS) 19 (2017), 2657–2695.Google Scholar
Eisenbud, D., Fløystad, G. and Weyman, J., The existence of equivariant pure free resolutions , Ann. Inst. Fourier (Grenoble) 61 (2011), 905–926; MR 2918721.Google Scholar
Eisenbud, D. and Schreyer, F.-O., Betti numbers of graded modules and cohomology of vector bundles , J. Amer. Math. Soc. 22 (2009), 859–888; MR 2505303.Google Scholar
Fink, A. and Speyer, D. E., K-classes for matroids and equivariant localization , Duke Math. J. 161 (2012), 2699–2723.Google Scholar
Fløystad, G., Boij–Söderberg theory: introduction and survey , in Combinatorics and homology, Proceedings in mathematics, Progress in Commutative Algebra, vol. 1 (de Gruyter, Berlin, 2012), 1–54.Google Scholar
Ford, N., Levinson, J. and Sam, S. V., Towards Boij–Söderberg theory for Grassmannians: the case of square matrices , Algebra Number Theory 12 (2018), 285–303.Google Scholar
Fulton, W., Young tableaux (Cambridge University Press, Cambridge, 1996).Google Scholar
Gheorghita, I. and Sam, S. V., The cone of Betti tables over three non-collinear points in the plane , J. Commut. Algebra 8 (2016), 537–548.Google Scholar
Grayson, D. R. and Stillman, M. E., Macaulay2, a software system for research in algebraic geometry, http://www.math.uiuc.edu/Macaulay2/.Google Scholar
Kostant, B. and Kumar, S., T-equivariant K-theory of generalized flag varieties , J. Differential Geom. 32 (1990), 549–603; MR 1072919.Google Scholar
Kummini, M. and Sam, S. V., The cone of Betti tables over a rational normal curve , in Commutative algebra and noncommutative algebraic geometry, Mathematical Sciences Research Institute Publications, vol. 68 (Cambridge University Press, Cambridge, 2015), 251–264.Google Scholar
D. Lampert, Bijection modeling isomorphism of infinite-dimensional vector spaces, MathOverflow, http://mathoverflow.net/q/243071 (version: 2016-06-27), (http://mathoverflow.net/users/59248/david-lampert).Google Scholar
Merkurjev, A. S., Equivariant K-theory, Handbook of K-theory, vols 1, 2 (Springer, Berlin, 2005), 925–954; MR 2181836.Google Scholar
Mumford, D. and Fogarty, J., Geometric invariant theory, Ergebnisse der Mathematik und ihrer Grenzgebiete [Results in Mathematics and Related Areas], vol. 34, second edition (Springer, Berlin, 1982); MR 719371.Google Scholar
The Sage Developers, Sagemath, the Sage Mathematics Software System, 2016, http://www.sagemath.org.Google Scholar
Nagel, U. and Sturgeon, S., Combinatorial interpretations of some Boij-Söderberg decompositions , J. Algebra 381 (2013), 54–72; MR 3030509.Google Scholar
Stanley, R. P., Enumerative combinatorics, Vol. 2, Cambridge Studies in Advanced Mathematics (Cambridge University Press, Cambridge, 1999), 583–585; errata et addenda.Google Scholar
Thomason, R. W., Algebraic K-theory of group scheme actions , in Algebraic topology and algebraic K-theory (Princeton, NJ, 1983), Annales of Mathematical Studies, vol. 113 (Princeton University Press, Princeton, NJ, 1987), 539–563; MR 921490.Google Scholar