Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-10T19:21:42.978Z Has data issue: false hasContentIssue false
  • English
  • Français

A formula for certain Shalika germs of ramified unitary groups

Part of: Lie groups

Published online by Cambridge University Press:  19 January 2017

Cheng-Chiang Tsai
Cheng-Chiang Tsai*
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, for nilpotent orbits of ramified quasi-split unitary groups with two Jordan blocks, we give closed formulas for their Shalika germs at certain equi-valued elements with half-integral depth previously studied by Hales. Associated with these elements are hyperelliptic curves defined over the residue field, and the numbers we obtain can be expressed in terms of Frobenius eigenvalues on the first 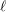$\ell$-adic cohomology of the curves, generalizing previous result of Hales on stable subregular Shalika germs. These Shalika germ formulas imply new results on stability and endoscopic transfer of nilpotent orbital integrals of ramified unitary groups. We also describe how the same numbers appear in the local character expansions of specific supercuspidal representations and consequently dimensions of degenerate Whittaker models.

Keywords

Shalika germsendoscopy

MSC classification

Primary: 22E35: Analysis on $p$-adic Lie groups
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 1 , January 2017 , pp. 175 - 213
Copyright
© The Author 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, J. D. and Spice, L., Supercuspidal characters of reductive p-adic groups , Amer. J. Math. 131 (2009), 1137–1210; MR 2543925 (2011a:22018).CrossRefGoogle Scholar
Assem, M., On stability and endoscopic transfer of unipotent orbital integrals on p-adic symplectic groups , Mem. Amer. Math. Soc. 134 (1998); MR 1415560 (98m:22013).Google Scholar
Bhargava, M. and Gross, B. H., The average size of the 2-Selmer group of Jacobians of hyperelliptic curves having a rational Weierstrass point , in Automorphic representations and L-functions, Tata Institute of Fundamental Research Studies in Mathematics, vol. 22 (Tata Institute of Fundamental Research, Mumbai, 2013), 23–91; MR 3156850.Google Scholar
Bhargava, M. and Gross, B. H., Arithmetic invariant theory , in Symmetry: representation theory and its applications, Progress in Mathematics, vol. 257 (Birkhäuser/Springer, New York, 2014), 33–54; MR 3363006.CrossRefGoogle Scholar
DeBacker, S., Homogeneity results for invariant distributions of a reductive p-adic group , Ann. Sci. Éc. Norm. Supér. (4) 35 (2002), 391–422; MR 1914003 (2003i:22019).CrossRefGoogle Scholar
Gordon, J. and Hales, T., Endoscopic transfer of orbital integrals in large residual characteristic , Amer. J. Math. 138 (2016), 109–148; MR 3462882.CrossRefGoogle Scholar
Goresky, M., Kottwitz, R. and MacPherson, R., Purity of equivalued affine Springer fibers , Represent. Theory 10 (2006), 130–146 (electronic); MR 2209851 (2007i:22025).CrossRefGoogle Scholar
Hales, T. C., Hyperelliptic curves and harmonic analysis (why harmonic analysis on reductive p-adic groups is not elementary) , in Representation theory and analysis on homogeneous spaces (New Brunswick, NJ, 1993), Contemporary Mathematics, vol. 177 (American Mathematical Society, Providence, RI, 1994), 137–169; MR 1303604 (96d:22024).CrossRefGoogle Scholar
Harish-Chandra, Admissible invariant distributions on reductive p-adic groups, University Lecture Series, vol. 16(American Mathematical Society, Providence, RI, 1999), Preface and notes by S. DeBacker and P. J. Sally, Jr; MR 1702257 (2001b:22015).Google Scholar
Kaletha, T., Epipelagic L-packets and rectifying characters , Invent. Math. 202 (2015), 1–89; MR 3402796.CrossRefGoogle Scholar
Langlands, R. P. and Shelstad, D., On the definition of transfer factors , Math. Ann. 278 (1987), 219–271; MR 909227 (89c:11172).CrossRefGoogle Scholar
Levy, P., Vinberg’s 𝜃-groups in positive characteristic and Kostant–Weierstrass slices , Transform. Groups 14 (2009), 417–461; MR 2504929 (2010g:17022).CrossRefGoogle Scholar
Lusztig, G. and Spaltenstein, N., Induced unipotent classes , J. Lond. Math. Soc. (2) 19 (1979), 41–52; MR 527733 (82g:20070).CrossRefGoogle Scholar
Mœglin, C. and Waldspurger, J.-L., Modèles de Whittaker dégénérés pour des groupes p-adiques , Math. Z. 196 (1987), 427–452; MR 913667 (89f:22024).CrossRefGoogle Scholar
Ngô, B. C., Le lemme fondamental pour les algèbres de Lie , Publ. Math. Inst. Hautes Études Sci. (2010), 1–169; MR 2653248 (2011h:22011).CrossRefGoogle Scholar
Ranga Rao, R., Orbital integrals in reductive groups , Ann. of Math. (2) 96 (1972), 505–510; MR 0320232 (47 #8771).Google Scholar
Reeder, M. and Yu, J.-K., Epipelagic representations and invariant theory , J. Amer. Math. Soc. 27 (2014), 437–477; MR 3164986.CrossRefGoogle Scholar
Shalika, J. A., A theorem on semi-simple p-adic groups , Ann. of Math. (2) 95 (1972), 226–242; MR 0323957 (48 #2310).CrossRefGoogle Scholar
Shelstad, D., A formula for regular unipotent germs , in Orbites unipotentes et représentations, II, Astérisque, vol. 171–172 (Société Mathématique de France, Paris, 1989), 275–277; MR 1021506 (91b:22012).Google Scholar
Springer, T. A. and Steinberg, R., Conjugacy classes , in Seminar on algebraic groups and related finite groups (The Institute for Advanced Study, Princeton, NJ, 1968/69), Lecture Notes in Mathematics, vol. 131 (Springer, Berlin, 1970), 167–266; MR 0268192 (42 #3091).CrossRefGoogle Scholar
Thorne, J. A., Vinberg’s representations and arithmetic invariant theory , Algebra Number Theory 7 (2013), 2331–2368; MR 3152016.CrossRefGoogle Scholar
Tsai, C.-C., Computations of orbital integrals and Shalika germs, arXiv:1512.00445v1 [math.RT].Google Scholar
Tsai, C.-C., Inductive structure of Shalika germs and affine Springer fibers, Preprint (2015),arXiv:1512.00445v1 [math.RT].Google Scholar
Waldspurger, J.-L., Le lemme fondamental implique le transfert , Compositio Math. 105 (1997), 153–236; MR 1440722 (98h:22023).CrossRefGoogle Scholar
Waldspurger, J.-L., Intégrales orbitales nilpotentes et endoscopie pour les groupes classiques non ramifiés, Astérisque, vol. 269 (Société Mathématique de France, Paris, 2001); MR 1817880 (2002h:22014).Google Scholar
Wang, X., Maximal linear spaces contained in the base loci of pencils of quadrics, Preprint (2013), arXiv:1302.2385 [math.AG].Google Scholar