Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Budur, Nero
and
Zhang, Ziyu
2019.
Formality conjecture for K3 surfaces.
Compositio Mathematica,
Vol. 155,
Issue. 5,
p.
902.
Budur, Nero
2021.
Rational Singularities, Quiver Moment Maps, and Representations of Surface Groups.
International Mathematics Research Notices,
Vol. 2021,
Issue. 15,
p.
11782.
Bandiera, Ruggero
Manetti, Marco
and
Meazzini, Francesco
2021.
Formality conjecture for minimal surfaces of Kodaira dimension 0.
Compositio Mathematica,
Vol. 157,
Issue. 2,
p.
215.
Li, Chunyi
Pertusi, Laura
and
Zhao, Xiaolei
2023.
Derived categories of hearts on Kuznetsov components.
Journal of the London Mathematical Society,
Vol. 108,
Issue. 6,
p.
2146.
Li, Zhiyuan
and
Zhang, Ruxuan
2023.
Beauville–Voisin Filtrations on Zero-Cycles of Moduli Space of Stable Sheaves on K3 Surfaces.
International Mathematics Research Notices,
Vol. 2023,
Issue. 13,
p.
11537.
Meazzini, Francesco
and
Onorati, Claudio
2023.
Hyper-holomorphic connections on vector bundles on hyper-Kähler manifolds.
Mathematische Zeitschrift,
Vol. 303,
Issue. 1,
Chen, Huachen
Pertusi, Laura
and
Zhao, Xiaolei
2024.
Some remarks about deformation theory and formality conjecture.
ANNALI DELL'UNIVERSITA' DI FERRARA,
Vol. 70,
Issue. 3,
p.
761.
Carocci, Francesca
Orecchia, Giulio
and
Wyss, Dimitri
2024.
BPS invariants fromp-adic integrals.
Compositio Mathematica,
Vol. 160,
Issue. 7,
p.
1525.
Beckmann, Thorsten
2024.
Atomic objects on hyper-Kähler manifolds.
Journal of Algebraic Geometry,
Vol. 34,
Issue. 1,
p.
109.
Davison, Ben
2024.
Purity and 2-Calabi–Yau categories.
Inventiones mathematicae,
Vol. 238,
Issue. 1,
p.
69.
Vernet, Tanguy
2024.
Rational Singularities for Moment Maps of Totally Negative Quivers.
Transformation Groups,
Arbarello, Enrico
and
Saccà, Giulia
2025.
Perspectives on Four Decades of Algebraic Geometry, Volume 1.
Vol. 351,
Issue. ,
p.
1.
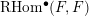 $\operatorname{RHom}^{\bullet }(F,F)$ is formal for any sheaf
$\operatorname{RHom}^{\bullet }(F,F)$ is formal for any sheaf 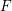 $F$ polystable with respect to an ample line bundle. Our main tool is the uniqueness of the DG enhancement of the bounded derived category of coherent sheaves. We also extend the formality result to derived objects that are polystable with respect to a generic Bridgeland stability condition.
$F$ polystable with respect to an ample line bundle. Our main tool is the uniqueness of the DG enhancement of the bounded derived category of coherent sheaves. We also extend the formality result to derived objects that are polystable with respect to a generic Bridgeland stability condition.

