Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T02:19:13.052Z Has data issue: false hasContentIssue false
  • English
  • Français

Foliations on unitary Shimura varieties in positive characteristic

Part of: Arithmetic problems. Diophantine geometry Arithmetic algebraic geometry

Published online by Cambridge University Press:  11 October 2018

Ehud de Shalit  and
Eyal Z. Goren
Ehud de Shalit
Affiliation:
Einstein Institute of Mathematics, Hebrew University of Jerusalem, Givat Ram, Jerusalem, Israel email [email protected]
Eyal Z. Goren
Affiliation:
Department of Mathematics and Statistics, McGill University, 805 Sherbrooke Street West, Montréal, QC, Canada email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

When 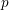$p$ is inert in the quadratic imaginary field 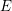$E$ and 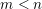$m<n$, unitary Shimura varieties of signature 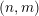$(n,m)$ and a hyperspecial level subgroup at 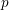$p$, carry a natural foliationof height 1 and rank 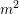$m^{2}$ in the tangent bundle of their special fiber 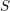$S$. We study this foliation and show that it acquires singularities at deep Ekedahl–Oort strata, but that these singularities are resolved if we pass to a natural smooth moduli problem 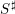$S^{\sharp }$, a successive blow-up of 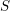$S$. Over the (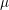$\unicode[STIX]{x1D707}$-)ordinary locus we relate the foliation to Moonen’s generalized Serre–Tate coordinates. We study the quotient of 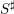$S^{\sharp }$ by the foliation, and identify it as the Zariski closure of the ordinary-étale locus in the special fiber 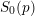$S_{0}(p)$ of a certain Shimura variety with parahoric level structure at 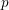$p$. As a result, we get that this ‘horizontal component’ of 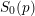$S_{0}(p)$, as well as its multiplicative counterpart, are non-singular (formerly they were only known to be normal and Cohen–Macaulay). We study two kinds of integral manifolds of the foliation: unitary Shimura subvarieties of signature 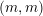$(m,m)$, and a certain Ekedahl–Oort stratum that we denote 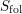$S_{\text{fol}}$. We conjecture that these are the only integral submanifolds.

Keywords

Shimura varietiesEkedahl–Oort stratafoliations

MSC classification

Primary: 11G18: Arithmetic aspects of modular and Shimura varieties 14G35: Modular and Shimura varieties
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 11 , November 2018 , pp. 2267 - 2304
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bültel, O. and Wedhorn, T., Congruence relations for Shimura varieties associated to some unitary groups , J. Inst. Math. Jussieu 5 (2006), 229–261.Google Scholar
Deligne, P. and Illusie, L., Relèvements modulo p 2 et décomposition du complexe de de Rham , Invent. Math. 89 (1987), 247–270.Google Scholar
de Shalit, E. and Goren, E. Z., A theta operator on Picard modular forms modulo an inert prime , Res. Math. Sci. 3 (2016), paper no. 28.Google Scholar
de Shalit, E. and Goren, E. Z., Theta operators on unitary Shimura varieties, Preprint (2017),arXiv:1712.06969.Google Scholar
de Shalit, E. and Goren, E. Z., On the bad reduction of certain U (2, 1) Shimura varieties , in Geometry, algebra, number theory and their information technology applications, Springer Proceedings in Mathematics & Statistics, eds Akbary, A. and Gun, S. (2018), to appear,arXiv:1703.05720.Google Scholar
Eisenbud, D., Commutative algebra with a view toward algebraic geometry, Graduate Texts in Mathematics, vol. 150 (Springer, New York, 1995).Google Scholar
Ekedahl, T., Foliations and inseparable morphisms , in Algebraic geometry, Bowdin 1985, Proceedings of Symposia in Pure Mathematics, vol. 46 (American Mathematical Society, Providence, RI, 1987), 139–149.Google Scholar
Goldring, W. and Nicole, M.-H., The 𝜇-ordinary Hasse invariant of unitary Shimura varieties , J. Reine Angew. Math. 728 (2017), 137–151.Google Scholar
Görtz, U., On the flatness of models of certain Shimura varieties of PEL type , Math. Ann. 321 (2001), 689–727.Google Scholar
Grothendieck, A., Groupes de Barsotti–Tate et cristaux de Dieudonné, Séminaire de Mathématiques Supérieures, vol. 45 (Les presses de l’Université de Montréal, 1974).Google Scholar
Harris, J., Algebraic geometry: a first course (Springer, New York, 1992).Google Scholar
Jacobson, N., Lectures in abstract algebra. III. Theory of fields and Galois theory, Graduate Texts in Mathematics, vol. 32 (Springer, New York–Heidelberg, 1975), Second corrected printing.Google Scholar
Katz, N., Nilpotent connections and the monodromy theorem: applications of a result of Turrittin , Publ. Math. Inst. Hautes Études Sci. 39 (1970), 175–232.Google Scholar
Kottwitz, R. E., Points on some Shimura varieties over finite fields , J. Amer. Math. Soc. 5 (1992), 373–444.Google Scholar
Kunz, E., Characterizations of regular local rings of characteristic p , Amer. J. Math. 91 (1969), 772–784.Google Scholar
Lan, K.-W., Arithmetic compactifications of PEL-type Shimura varieties, London Mathematical Society Monographs, vol. 36 (Princeton University Press, Princeton, 2013).Google Scholar
Miyaoka, Y., Deformation of a morphism along a foliation , in Algebraic geometry, Bowdin 1985, Proceedings of Symposia in Pure Mathematics, vol. 46 (American Mathematical Society, Providence, RI, 1987), 245–268.Google Scholar
Moonen, B., Group schemes with additional structures and Weyl group elements , in Moduli of abelian varieties, Progress in Mathematics, vol. 195, eds Faber, C., van der Geer, G. and Oort, F. (Birkhäuser, Basel, 2001), 255–298.Google Scholar
Moonen, B., Serre–Tate theory for moduli spaces of PEL type , Ann. Sci. Éc. Norm. Supér. (4) 37 (2004), 223–269.Google Scholar
Oort, F., A stratification of a moduli space of abelian varieties , in Moduli of abelian varieties, Progress in Mathematics, vol. 195, eds Faber, C., van der Geer, G. and Oort, F. (Birkhäuser, 2001), 345–416.Google Scholar
Pappas, G. and Zhu, X., Local models of Shimura varieties and a conjecture of Kottwitz , Invent. Math. 194 (2013), 147–254.Google Scholar
Rapoport, M. and Zink, T., Period spaces for p-divisible groups, Annals of Mathematics Studies, vol. 141 (Princeton University Press, Princeton, 1996).Google Scholar
Raynaud, M., Schémas en groupes de type (p, …, p) , Bull. Soc. Math. France 102 (1974), 241–250.Google Scholar
Rudakov, A. N. and Shafarevich, I. R., Inseparable morphisms of algebraic surfaces , Izv. Akad. Nauk SSSR Ser. Mat. 40 (1976), 1269–1307.Google Scholar
Vasiu, A., Manin problems for Shimura varieties of Hodge type , J. Ramanujan Math. Soc. 26 (2011), 31–84.Google Scholar
Viehmann, E. and Wedhorn, T., Ekedahl–Oort and Newton strata for Shimura varieties of PEL type , Math. Ann. 356 (2013), 1493–1550.Google Scholar
Wedhorn, T., The dimension of Oort strata of Shimura varieties of PEL-type , in Moduli of abelian varieties, Progress in Mathematics, vol. 195, eds Faber, C., van der Geer, G. and Oort, F. (Birkhäuser, 2001), 441–471.Google Scholar
Wooding, A., The Ekedahl–Oort stratification of unitary Shimura varieties, PhD thesis, McGill University (2016).Google Scholar