Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-02-22T21:02:37.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Fast growth of the number of periodic points arising from heterodimensional connections

Part of: Dynamical systems with hyperbolic behavior Smooth dynamical systems: general theory Local and nonlocal bifurcation theory

Published online by Cambridge University Press:  02 August 2021

Masayuki Asaoka ,
Katsutoshi Shinohara  and
Dmitry Turaev
Masayuki Asaoka
Affiliation:
Faculty of Science and Engineering, Doshisha University, 1-3 Tatara Miyakodani, Kyotanabe610-0394, [email protected]
Katsutoshi Shinohara
Affiliation:
Graduate School of Commerce and Management, Hitotsubashi University, 2-1 Naka, Kunitachi, Tokyo186-8601, [email protected]
Dmitry Turaev
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen's Gate, London, [email protected] Higher School of Economics – Nizhny Novgorod, Russia
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider 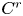$C^{r}$-diffeomorphisms (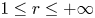$1 \leq r \leq +\infty$) of a compact smooth manifold having two pairs of hyperbolic periodic points of different indices which admit transverse heteroclinic points and are connected through a blender. We prove that, by giving an arbitrarily 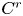$C^{r}$-small perturbation near the periodic points, we can produce a periodic point for which the first return map in the center direction coincides with the identity map up to order 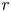$r$, provided the transverse heteroclinic points satisfy certain natural conditions involving higher derivatives of their transition maps in the center direction. As a consequence, we prove that 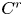$C^{r}$-generic diffeomorphisms in a small neighborhood of the diffeomorphism under consideration exhibit super-exponential growth of number of periodic points. We also give examples which show the necessity of the conditions we assume.

Keywords

partially hyperbolic diffeomorphismsgrowth of periodic pointsheterodimensional cyclesblenders

MSC classification

Primary: 37C35: Orbit growth
Secondary: 37D30: Partially hyperbolic systems and dominated splittings 37G25: Bifurcations connected with nontransversal intersection
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 9 , September 2021 , pp. 1899 - 1963
Copyright
© 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdenur, F., Bonatti, C., Crovisier, S., Díaz, L. J. and Wen, L., Periodic points and homoclinic classes, Ergodic Theory Dynam. Systems 27 (2007), 1–22.CrossRefGoogle Scholar
Artin, M. and Mazur, B., On periodic points, Ann. Math. 81 (1965), 82–99.CrossRefGoogle Scholar
Asaoka, M., Shinohara, K. and Turaev, D., Degenerate behavior in non-hyperbolic semi-group actions on the interval: fast growth of periodic points and universal dynamics, Math. Ann. 368 (2017), 1277–1309.CrossRefGoogle Scholar
Berger, P., Generic family displaying robustly a fast growth of the number of periodic points, Preprint (2017), arXiv:1701.02393.Google Scholar
Bochi, J., Bonatti, C. and Díaz, L. J., Robust criterion for the existence of nonhyperbolic ergidic measures, Comm. Math. Phys. 344 (2016), 751–795.CrossRefGoogle Scholar
Bonatti, C. and Díaz, L. J., Persistent nonhyperbolic transitive diffeomorphisms, Ann. Math. (2) 143 (1996), 357–396.CrossRefGoogle Scholar
Bonatti, C. and Díaz, L. J., Robust heterodimensional cycles and $C^{1}$-generic dynamics, J. Inst. Math. Jussieu 7 (2008), 469–525.CrossRefGoogle Scholar
Bonatti, C. and Díaz, L. J., Abundance of $C^{1}$-robust homoclinic tangencies, Trans. Amer. Math. Soc. 364 (2012), 5111–5148.CrossRefGoogle Scholar
Bonatti, C., Díaz, L. J. and Fisher, T., Super-exponential growth of the number of periodic orbits inside homoclinic classes, Discrete Contin. Dyn. Syst. 20 (2008), 589–604.CrossRefGoogle Scholar
Bonatti, C., Díaz, L. and Pujals, E., A $C^{1}$-generic dichotomy for diffeomorphisms: weak forms of hyperbolicity or infinitely many sinks or sources, Ann. Math. 158 (2003), 355–418.CrossRefGoogle Scholar
Bonatti, C., Díaz, L. J. and Ures, R., Minimality of strong stable and unstable foliations for partially hyperbolic diffeomorphisms, J. Inst. Math. Jussieu 1 (2002), 513–541.CrossRefGoogle Scholar
Bonatti, C., Díaz, L. J. and Viana, M., Dynamics beyond uniform hyperbolicity (Springer, 2004).Google Scholar
Bowen, R., Equilibrium states and the ergodic theory of Anosov diffeomorphisms, Lecture Notes in Mathematics, vol. 470 (Springer, Berlin, 2008).CrossRefGoogle Scholar
Díaz, L. J., Persistence of cycles and nonhyperbolic dynamics at heteroclinic bifurcations, Nonlinearity 8 (1995), 693–715.CrossRefGoogle Scholar
Díaz, L. J. and Gorodetski, A., Non-hyperbolic ergodic measures for non-hyperbolic homoclinic classes, Ergodic Theory Dynam. Systems 29 (2009), 1479–1513.CrossRefGoogle Scholar
Díaz, L. J., Kiriki, S. and Shinohara, K., Blenders in centre unstable Hénon-like families: with an application to heterodimensional bifurcations, Nonlinearity 27 (2014), 353–378.CrossRefGoogle Scholar
Díaz, L. J. and Rocha, J., Heterodimensional cycles, partial hyperbolicity and limit dynamics, Fund. Math. 174 (2002), 127–186.CrossRefGoogle Scholar
Esteves, S., Growth of number of periodic orbits of one family of skew product maps, Dyn. Syst. 33 (2018), 10–26.CrossRefGoogle Scholar
Gonchenko, S. V., Shilnikov, L. P. and Turaev, D. V., On dynamical properties of multidimensional diffeomorphisms from Newhouse regions. I, Nonlinearity 21 (2008), 923–972.CrossRefGoogle Scholar
Gorodetski, A., Ilyashenko, Yu., Kleptsyn, V. and Nalsky, M., Non-removable zero Lyapunov exponents, Funct. Anal. Appl. 39 (2005), 27–38.CrossRefGoogle Scholar
Hayashi, S., Connecting invariant manifolds and the solution of the $C^{1}$-stability and $\Omega$-stability conjectures for flows, Ann. Math. 145 (1997), 81–137.CrossRefGoogle Scholar
Hirsch, M., Pugh, C. and Shub, M., Invariant manifolds, Lecture Notes in Mathematics, vol. 583 (Springer, 1977).CrossRefGoogle Scholar
Kaloshin, V., An extension of the Artin-Mazur theorem, Ann. Math. 150 (1999), 729–741.CrossRefGoogle Scholar
Kaloshin, V., Generic diffeomorphisms with Super-exponential growth of number of periodic orbits, Comm. Math. Phys. 211 (2000), 253–271.CrossRefGoogle Scholar
Kaloshin, V. and Kozlovski, O. S., A $C^{r}$ unimodal map with an arbitrary fast growth of the number of periodic points, Ergodic Theory Dynam. Systems 32 (2012), 159–165.CrossRefGoogle Scholar
Martens, M., de Melo, W. and van Strien, S., Julia-Fatou-Sullivan theory for real one-dimensional dynamics, Acta Math. 168 (1992), 273–318.CrossRefGoogle Scholar
Newhouse, S., The abundance of wild hyperbolic sets and non-smooth stable sets for diffeomorphisms, Publ. Math. Inst. Hautes Études Sci. 50 (1979), 101–151.CrossRefGoogle Scholar
Palis, J., A global view of dynamics and a conjecture on the denseness of finitude of attractors, Asterisque 261 (2000), 339–351.Google Scholar
Palis, J. and Takens, F., Hyperbolicity and sensitive chaotic dynamics at homoclinic bifurcations, Cambridge Studies in Advanced Mathematics, vol. 35 (1993).Google Scholar
Shilnikov, L., Shilnikov, A., Turaev, D. and Chua, L., Methods of qualitative theory in nonlinear dynamics. Part I (World Scientific, 1998).CrossRefGoogle Scholar
Shub, M., Global stability of dynamical systems (Springer, 1987).CrossRefGoogle Scholar
Shub, M. and Wilkinson, A., Pathological foliations and removable zero exponents, Invent. Math. 139 (2000), 495–508.CrossRefGoogle Scholar
Sternberg, S., Local contractions and a theorem of Poincaré, Amer. J. Math. 79 (1957), 809–824.CrossRefGoogle Scholar
Takens, F., Partially hyperbolic fixed points, Topology 10 (1971), 133–147.CrossRefGoogle Scholar
Turaev, D. V., On dimension of non-local bifurcational problems, Internat. J. Bifur. Chaos 6 (1996), 919–948.CrossRefGoogle Scholar
Turaev, D., Richness of chaos in the absolute Newhouse domain, Proceedings of the International Congress of Mathematicians 2010 (ICM 2010), vol. III (Hindustan Book Agency, New Delhi, 2011).CrossRefGoogle Scholar
Turaev, D., Maps close to identity and universal maps in the Newhouse domain, Comm. Math. Phys. 335 (2015), 1235–1277.CrossRefGoogle Scholar