Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T00:09:27.604Z Has data issue: false hasContentIssue false
  • English
  • Français

The existence of Zariski dense orbits for polynomial endomorphisms of the affine plane

Part of: Holomorphic mappings and correspondences Arithmetic and non-Archimedean dynamical systems

Published online by Cambridge University Press:  31 May 2017

Junyi Xie
Junyi Xie*
Affiliation:
Université de Rennes I, Campus de Beaulieu, bâtiment 22–23, 35042 Rennes cedex, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

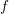In this paper we prove the following theorem. Let $f$ be a dominant polynomial endomorphism of the affine plane defined over an algebraically closed field of characteristic 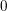$0$. If there is no nonconstant invariant rational function under $f$, then there exists a closed point in the plane whose orbit under 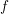$f$ is Zariski dense. This result gives us a positive answer to a conjecture proposed by Medvedev and Scanlon, by Amerik, Bogomolov and Rovinsky, and by Zhang for polynomial endomorphisms of the affine plane.

Keywords

polynomial endomorphismorbitvaluative tree

MSC classification

Primary: 37P55: Arithmetic dynamics on general algebraic varieties 32H50: Iteration problems
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 8 , August 2017 , pp. 1658 - 1672
Copyright
© The Author 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abate, M., An introduction to hyperbolic dynamical systems (Istituti Editoriali e Poligrafici Internazionali, Pisa, 2001).Google Scholar
Amerik, E., Existence of non-preperiodic algebraic points for a rational self-map of infinite order , Math. Res. Lett. 18 (2011), 251–256.Google Scholar
Amerik, E., Bogomolov, F. and Rovinsky, M., Remarks on endomorphisms and rational points , Compositio Math. 147 (2011), 1819–1842.Google Scholar
Amerik, E. and Campana, F., Fibrations méromorphes sur certaines variétés à fibré canonique trivial , Pure Appl. Math. Q. 4 (2008), 509–545.Google Scholar
Bell, J. P., A generalised Skolem–Mahler–Lech theorem for affine varieties , J. Lond. Math. Soc. (2) 73 (2006), 367–379.Google Scholar
Bell, J. P., Ghioca, D. and Tucker, T. J., Applications of p-adic analysis for bounding periods of subvarieties under étale maps , Int. Math. Res. Not. IMRN 2015 (2015), 3576–3597.Google Scholar
Cantat, S., Invariant hypersurfaces in holomorphic dynamics , Math. Res. Lett. 17 (2010), 833–841.Google Scholar
Fakhruddin, N., Questions on self maps of algebraic varieties , J. Ramanujan Math. Soc. 18 (2003), 109–122.Google Scholar
Fakhruddin, N., The algebraic dynamics of generic endomorphisms of ℙ n , Algebra Number Theory 8 (2014), 587–608.Google Scholar
Favre, C. and Jonsson, M., The valuative tree, Lecture Notes in Mathematics, vol. 1853 (Springer, Berlin, 2004).Google Scholar
Favre, C. and Jonsson, M., Eigenvaluations , Ann. Sci. Éc. Norm. Supér. (4) 40 (2007), 309–349.Google Scholar
Favre, C. and Jonsson, M., Dynamical compactifications of C 2 , Ann. of Math. (2) 173 (2011), 211–248.Google Scholar
Jonsson, M., Dynamics on Berkovich spaces in low dimensions , in Berkovich spaces and applications, Lecture Notes in Mathematics, vol. 2119, eds Nicaise, J., Ducros, A. and Favre, C. (Springer, 2015), 205–366.Google Scholar
Medvedev, A. and Scanlon, T., Polynomial dynamics, Preprint (2009), arXiv:0901.2352v1.Google Scholar
Medvedev, A. and Scanlon, T., Invariant varieties for polynomial dynamical systems , Ann. of Math. (2) 179 (2014), 81–177.Google Scholar
Poonen, B., p-adic interpolation of iterates , Bull. Lond. Math. Soc. 46 (2014), 525–527.Google Scholar
Xie, J., When the intersection of valuation rings of $k[x,y]$ has transcendence degree 2? Preprint (2014), arXiv:1403.6052.Google Scholar
Xie, J., The dynamical Mordell–Lang conjecture for polynomial endomorphisms on the affine plane, Preprint (2015), arXiv:1503.00773.Google Scholar
Xie, J., Periodic points of birational transformations on projective surfaces , Duke Math. J. 164 (2015), 903–932.Google Scholar
Zhang, S.-W., Distributions in algebraic dynamics, Surveys in Differential Geometry, vol. 10 (International Press, Somerville, MA, 2006), 381–430.Google Scholar