Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T02:31:32.041Z Has data issue: false hasContentIssue false
  • English
  • Français

Excision in algebraic 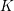$K$-theory revisited

Part of: Higher algebraic $K$-theory Abelian categories

Published online by Cambridge University Press:  06 August 2018

Georg Tamme
Georg Tamme*
Affiliation:
Fakultät für Mathematik, Universität Regensburg, D-93040 Regensburg, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

By a theorem of Suslin, a Tor-unital (not necessarily unital) ring satisfies excision in algebraic 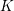$K$-theory. We give a new and direct proof of Suslin’s result based on an exact sequence of categories of perfect modules. In fact, we prove a more general descent result for a pullback square of ring spectra and any localizing invariant. Our descent theorem contains not only Suslin’s result, but also Nisnevich descent of algebraic 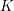$K$-theory for affine schemes as special cases. Moreover, the role of the Tor-unitality condition becomes very transparent.

Keywords

excisionlocalizing invariantalgebraic K-theory

MSC classification

Primary: 18E30: Derived categories, triangulated categories
Secondary: 19D99: None of the above, but in this section
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 9 , September 2018 , pp. 1801 - 1814
Copyright
© The Author 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author is supported by the CRC 1085 Higher Invariants (Universität Regensburg) funded by the DFG.

References

Asok, A., Hoyois, M. and Wendt, M., Affine representability results in A1 -homotopy theory, I: vector bundles , Duke Math. J. 166 (2017), 1923–1953.Google Scholar
Blumberg, A., Gepner, D. and Tabuada, G., A universal characterization of higher algebraic K-theory , Geom. Topol. 17 (2013), 733–838.Google Scholar
Blumberg, A. and Mandell, M., Localization theorems in topological Hochschild homology and topological cyclic homology , Geom. Topol. 16 (2012), 1053–1120.Google Scholar
Cortiñas, G., The obstruction to excision in K-theory and in cyclic homology , Invent. Math. 164 (2006), 143–173.Google Scholar
Dundas, B. and Kittang, H., Excision for K-theory of connective ring spectra , Homology, Homotopy Appl. 10 (2008), 29–39.Google Scholar
Dundas, B. and Kittang, H., Integral excision for K-theory , Homology Homotopy Appl. 15 (2013), 1–25.Google Scholar
Geisser, T. and Hesselholt, L., Bi-relative algebraic K-theory and topological cyclic homology , Invent. Math. 166 (2006), 359–395.Google Scholar
Joyal, A., The theory of quasi-categories and its applications, Quadern 45, Vol. II (Centre de Recerca Matematica, Barcelona, 2008).Google Scholar
Keller, B., A remark on the generalized smashing conjecture , Manuscripta Math. 84 (1994), 193–198.Google Scholar
Lurie, J., Higher topos theory, Annals of Mathematics Studies, vol. 170 (Princeton University Press, Princeton, NJ, 2009).Google Scholar
Lurie, J., Higher algebra (2017), http://www.math.harvard.edu/∼lurie/.Google Scholar
Lurie, J., Spectral algebraic geometry (2017), http://www.math.harvard.edu/∼lurie/.Google Scholar
Milne, J., Étale cohomology, Princeton Mathematical Series, vol. 33 (Princeton University Press, Princeton, NJ, 1980).Google Scholar
Morrow, M., Pro unitality and pro excision in algebraic K-theory and cyclic homology , J. Reine Angew. Math. 736 (2018), 95–139.Google Scholar
Neeman, A., The connection between the K-theory localization theorem of Thomason, Trobaugh and Yao and the smashing subcategories of Bousfield and Ravenel , Ann. Sci. Éc. Norm. Supér. (4) 25 (1992), 547–566.Google Scholar
Neeman, A. and Ranicki, A., Noncommutative localisation in algebraic K-theory. I , Geom. Topol. 8 (2004), 1385–1425.Google Scholar
Schlichting, M., Higher algebraic K-theory , in Topics in algebraic and topological K-theory, Lecture Notes in Mathematics, vol. 2008 (Springer, Berlin, 2011), 167–241.Google Scholar
Suslin, A., Excision in the integral algebraic K-theory , Tr. Mat. Inst. Steklova 208 (1995), 290–317.Google Scholar
Suslin, A. and Wodzicki, M., Excision in algebraic K-theory , Ann. of Math. (2) 136 (1992), 51–122.Google Scholar
Thomason, R. and Trobaugh, T., Higher algebraic K-theory of schemes and of derived categories , in The Grothendieck Festschrift, Vol. III, Progress in Mathematics, vol. 88 (Birkhäuser Boston, Boston, MA, 1990), 247–435.Google Scholar
Wodzicki, M., Excision in cyclic homology and in rational algebraic K-theory , Ann. of Math. (2) 129 (1989), 591–639.Google Scholar