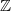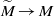Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Frączek, Krzysztof
and
Ulcigrai, Corinna
2014.
Ergodic Directions for Billiards in a Strip with Periodically Located Obstacles.
Communications in Mathematical Physics,
Vol. 327,
Issue. 2,
p.
643.
Schmoll, Martin
and
Johnson, Chris
2014.
Pseudo-Anosov eigenfoliations on Panov planes.
Electronic Research Announcements in Mathematical Sciences,
Vol. 21,
Issue. 0,
p.
89.
Frączek, Krzysztof
and
Ulcigrai, Corinna
2014.
Non-ergodic $\mathbb{Z}$ -periodic billiards and infinite translation surfaces.
Inventiones mathematicae,
Vol. 197,
Issue. 2,
p.
241.
Einsiedler, M.
Kadyrov, S.
and
Pohl, A.
2015.
Escape of mass and entropy for diagonal flows in real rank one situations.
Israel Journal of Mathematics,
Vol. 210,
Issue. 1,
p.
245.
Sabogal, Alba Málaga
and
Troubetzkoy, Serge
2016.
Minimality of the Ehrenfest wind-tree model.
Journal of Modern Dynamics,
Vol. 10,
Issue. 02,
p.
209.
Málaga Sabogal, Alba
and
Troubetzkoy, Serge
2016.
Ergodicity of the Ehrenfest wind–tree model.
Comptes Rendus. Mathématique,
Vol. 354,
Issue. 10,
p.
1032.
Artigiani, Mauro
2017.
Exceptional ergodic directions in Eaton lenses.
Israel Journal of Mathematics,
Vol. 220,
Issue. 1,
p.
29.
Treviño, Rodrigo
2018.
Flat surfaces, Bratteli diagrams and unique ergodicity à la Masur.
Israel Journal of Mathematics,
Vol. 225,
Issue. 1,
p.
35.
Frączek, Krzysztof
and
Hubert, Pascal
2018.
Recurrence and non‐ergodicity in generalized wind‐tree models.
Mathematische Nachrichten,
Vol. 291,
Issue. 11-12,
p.
1686.
Hooper, W.
2018.
Immersions and translation structures I: The space of structures on the pointed disk.
Conformal Geometry and Dynamics of the American Mathematical Society,
Vol. 22,
Issue. 11,
p.
235.
Frączek, Krzysztof
and
Schmoll, Martin
2018.
On Ergodicity of Foliations on
$${\mathbb{Z}^d}$$
Z
d
-Covers of Half-Translation Surfaces and Some Applications to Periodic Systems of Eaton Lenses.
Communications in Mathematical Physics,
Vol. 362,
Issue. 2,
p.
609.
HOOPER, W. PATRICK
and
TREVIÑO, RODRIGO
2019.
Indiscriminate covers of infinite translation surfaces are innocent, not devious.
Ergodic Theory and Dynamical Systems,
Vol. 39,
Issue. 8,
p.
2071.
Attarchi, Hassan
Bolding, Mark
and
Bunimovich, Leonid A.
2020.
Ehrenfests’ Wind–Tree Model is Dynamically Richer than the Lorentz Gas.
Journal of Statistical Physics,
Vol. 180,
Issue. 1-6,
p.
440.
Šarić, Dragomir
2022.
The Heights Theorem for infinite Riemann surfaces.
Geometriae Dedicata,
Vol. 216,
Issue. 3,
Beck, J.
Chen, W. W. L.
and
Yang, Y.
2022.
Quantitative behavior of non-integrable systems. III.
Acta Mathematica Hungarica,
Vol. 166,
Issue. 2,
p.
254.
Frączek, Krzysztof
and
Ulcigrai, Corinna
2022.
Encyclopedia of Complexity and Systems Science.
p.
1.
Frączek, Krzysztof
and
Ulcigrai, Corinna
2023.
Ergodic Theory.
p.
333.