Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-16T20:55:55.797Z Has data issue: false hasContentIssue false
  • English
  • Français

Duality for relative logarithmic de Rham–Witt sheaves and wildly ramified class field theory over finite fields

Part of: Algebraic number theory: global fields Arithmetic problems. Diophantine geometry (Co)homology theory

Published online by Cambridge University Press:  07 May 2018

Uwe Jannsen ,
Shuji Saito  and
Yigeng Zhao
Uwe Jannsen
Affiliation:
Fakultät für Mathematik, Universität Regensburg, 93040 Regensburg, Germany email [email protected]
Shuji Saito
Affiliation:
Interactive Research Center of Science, Graduate School of Science and Engineering, Tokyo Institute of Technology, 2-12-1 Okayama, Meguro, Tokyo 152-8551, Japan email [email protected]
Yigeng Zhao
Affiliation:
Fakultät für Mathematik, Universität Regensburg, 93040 Regensburg, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In order to study 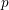$p$-adic étale cohomology of an open subvariety 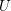$U$ of a smooth proper variety 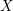$X$ over a perfect field of characteristic 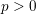$p>0$, we introduce new 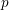$p$-primary torsion sheaves. It is a modification of the logarithmic de Rham–Witt sheaves of 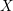$X$ depending on effective divisors 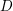$D$ supported in 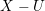$X-U$. Then we establish a perfect duality between cohomology groups of the logarithmic de Rham–Witt cohomology of 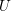$U$ and an inverse limit of those of the mentioned modified sheaves. Over a finite field, the duality can be used to study wildly ramified class field theory for the open subvariety 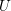$U$.

Keywords

logarithmic de Rham–Witt sheavesclass field theorywild ramificationétale dualityquasi-algebraic groups

MSC classification

Primary: 14F20: Étale and other Grothendieck topologies and (co)homologies
Secondary: 14F35: Homotopy theory; fundamental groups 11R37: Class field theory 14G17: Positive characteristic ground fields
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 6 , June 2018 , pp. 1306 - 1331
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Artin, M., Algebraic approximation of structures over complete local rings , Publ. Math. Inst. Hautes Études Sci. 36 (1969), 23–58.CrossRefGoogle Scholar
Bass, H. and Tate, J., The Milnor ring of a global field , in Algebraic K-Theory II: Classical algebraic K-theory, and connections with arithmetic (Springer, Berlin, Heidelberg, 1973), 347–446.Google Scholar
Berthelot, P., Le théorème de dualité plate pour les surfaces (d’après J.S. Milne) , in Surfaces algébriques (Springer, Berlin, Heidelberg, 1981), 203–237.CrossRefGoogle Scholar
Bloch, S. and Kato, K., p-adic etale cohomology , Publ. Math. Inst. Hautes Études Sci. 63 (1986), 107–152.CrossRefGoogle Scholar
Colliot-Thélène, J., Sansuc, J. and Soulé, C., Torsion dans le groupe de Chow de codimension deux , Duke Math. J. 50 (1983), 763–801.CrossRefGoogle Scholar
Geisser, T. and Hesselholt, L., The de Rham–Witt complex and p-adic vanishing cycles , J. Amer. Math. Soc. 19 (2006), 1–36.CrossRefGoogle Scholar
Geisser, T. and Levine, M., The K-theory of fields in characteristic p , Invent. Math. 139 (2000), 459–493.CrossRefGoogle Scholar
Gros, M. and Suwa, N., La conjecture de Gersten pour les faisceaux de Hodge–Witt logarithmique , Duke Math. J. 57 (1988), 615–628.CrossRefGoogle Scholar
Hyodo, O. and Kato, K., Semi-stable reduction and crystalline cohomology with logarithmic poles, in Périodes p-adiques, Bures-sur-Yvette, 1988 , Astérisque vol. 223 (Société Mathématique de France, Paris, 1994), 221–268; MR 1293974.Google Scholar
Illusie, L., Complexe de de Rham-Witt et cohomologie cristalline , Ann. Sci. Éc. Norm. Supér. (4) 12 (1979), 501–661.CrossRefGoogle Scholar
Kato, K., Galois cohomology of complete discrete valuation fields , in Algebraic K-theory, Lecture Notes in Mathematics, vol. 967, ed. Dennis, R. K. (Springer, Berlin, Heidelberg, 1982), 215–238.CrossRefGoogle Scholar
Kato, K., Duality theories for the p-primary étale cohomology I , in Algebraic and topological theories (Kinokuniya-shoten, Tokyo, 1985), 127–148.Google Scholar
Kato, K., Existence theorem for higher local fields , in Invitation to higher local fields (Geometry & Topology Publications, Coventry, 2000), 165–195.Google Scholar
Kerz, M., Milnor K-theory of local rings with finite residue fields , J. Algebraic Geom. 19 (2010), 173–191.CrossRefGoogle Scholar
Lorenzon, P., Logarithmic Hodge–Witt forms and Hyodo–Kato cohomology , J. Algebra 249 (2002), 247–265; MR 1901158.CrossRefGoogle Scholar
Milne, J. S., Duality in the flat cohomology of a surface , Ann. Sci. Éc. Norm. Supér. (4) 9 (1976), 171–201; MR 0460331.CrossRefGoogle Scholar
Milne, J. S., Values of zeta functions of varieties over finite fields , Amer. J. Math. 108 (1986), 297–360.CrossRefGoogle Scholar
Pépin, C., Dualité sur un corps local de caractéristique positive à corps résiduel algébriquement clos, Preprint (2014), arXiv:1411.0742.Google Scholar
Rost, M., Chow groups with coefficients , Doc. Math. 1 (1996), 319–393.CrossRefGoogle Scholar
Rülling, K. and Saito, S., Higher Chow groups with modulus and relative Milnor K-theory , Trans. Amer. Math. Soc. 370 (2018), 987–1043.CrossRefGoogle Scholar
Saito, S., A global duality theorem for varieties over global fields , in Algebraic K-theory: connections with geometry and topology (Kluwer, Dordrecht, 1989), 425–444.CrossRefGoogle Scholar
P. Deligne avec la collaboration de J. F. Boutot, A. Grothendieck, L. Illusie et J. L. Verdier, Cohomologie étale (SGA 4½), Lecture Notes in Mathematics, vol. 569 (Springer, Berlin, Heidelberg, 1977).CrossRefGoogle Scholar
Zhao, Y., Duality for relative logarithmic de Rham-Witt sheaves on semistable schemes over $\mathbb{F}_{q}[[t]]$ , Preprint (2016), arXiv:1611.08722.Google Scholar