Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Diverio, Simone
2009.
Existence of global invariant jet differentials on projective hypersurfaces of high degree.
Mathematische Annalen,
Vol. 344,
Issue. 2,
p.
293.
Diverio, Simone
Merker, Joël
and
Rousseau, Erwan
2010.
Effective algebraic degeneracy.
Inventiones mathematicae,
Vol. 180,
Issue. 1,
p.
161.
Diverio, Simone
and
Trapani, Stefano
2010.
A remark on the codimension of the Green–Griffiths locus of generic projective hypersurfaces of high degree.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2010,
Issue. 649,
Merker, Joël
2010.
Application of computational invariant theory to Kobayashi hyperbolicity and to Green–Griffiths algebraic degeneracy.
Journal of Symbolic Computation,
Vol. 45,
Issue. 10,
p.
986.
Pacienza, Gianluca
and
Rousseau, Erwan
2011.
Generalized Demailly–Semple jet bundles and holomorphic mappings into complex manifolds.
Journal de Mathématiques Pures et Appliquées,
Vol. 96,
Issue. 2,
p.
109.
Demailly, Jean-Pierre
2013.
Pluripotential Theory.
Vol. 2075,
Issue. ,
p.
143.
Brotbek, Damian
2014.
Hyperbolicity related problems for complete intersection varieties.
Compositio Mathematica,
Vol. 150,
Issue. 3,
p.
369.
Diverio, Simone
and
Rousseau, Erwan
2016.
Hyperbolicity of Projective Hypersurfaces.
p.
37.
Diverio, Simone
and
Rousseau, Erwan
2016.
Hyperbolicity of Projective Hypersurfaces.
p.
51.
Brotbek, Damian
2016.
Symmetric differential forms on complete intersection varieties and applications.
Mathematische Annalen,
Vol. 366,
Issue. 1-2,
p.
417.
Brotbek, Damian
2017.
On the hyperbolicity of general hypersurfaces.
Publications mathématiques de l'IHÉS,
Vol. 126,
Issue. 1,
p.
1.
Bérczi, Gergely
2019.
Towards the Green–Griffiths–Lang conjecture via equivariant localisation.
Proceedings of the London Mathematical Society,
Vol. 118,
Issue. 5,
p.
1057.
Demailly, Jean-Pierre
2020.
Recent results on the Kobayashi and Green-Griffiths-Lang conjectures.
Japanese Journal of Mathematics,
Vol. 15,
Issue. 1,
p.
1.
Campana, Frédéric
Darondeau, Lionel
and
Rousseau, Erwan
2020.
Orbifold hyperbolicity.
Compositio Mathematica,
Vol. 156,
Issue. 8,
p.
1664.


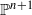 . In this paper we find an effective lower bound for the degree of
. In this paper we find an effective lower bound for the degree of 