Article contents
Derived categories of 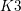 $K3$ surfaces, O’Grady’s filtration, and zero-cycles on holomorphic symplectic varieties
$K3$ surfaces, O’Grady’s filtration, and zero-cycles on holomorphic symplectic varieties
Published online by Cambridge University Press: 26 November 2019
Abstract
Moduli spaces of stable objects in the derived category of a  $K3$ surface provide a large class of holomorphic symplectic varieties. In this paper, we study the interplay between Chern classes of stable objects and zero-cycles on holomorphic symplectic varieties which arise as moduli spaces. First, we show that the second Chern class of any object in the derived category lies in a suitable piece of O’Grady’s filtration on the
$K3$ surface provide a large class of holomorphic symplectic varieties. In this paper, we study the interplay between Chern classes of stable objects and zero-cycles on holomorphic symplectic varieties which arise as moduli spaces. First, we show that the second Chern class of any object in the derived category lies in a suitable piece of O’Grady’s filtration on the 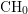 $\text{CH}_{0}$-group of the
$\text{CH}_{0}$-group of the 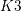 $K3$ surface. This solves a conjecture of O’Grady and improves on previous results of Huybrechts, O’Grady, and Voisin. Second, we propose a candidate for the Beauville–Voisin filtration on the
$K3$ surface. This solves a conjecture of O’Grady and improves on previous results of Huybrechts, O’Grady, and Voisin. Second, we propose a candidate for the Beauville–Voisin filtration on the 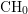 $\text{CH}_{0}$-group of the moduli space of stable objects. We discuss its connection with Voisin’s recent proposal via constant cycle subvarieties, and prove a conjecture of hers on the existence of special algebraically coisotropic subvarieties for the moduli space.
$\text{CH}_{0}$-group of the moduli space of stable objects. We discuss its connection with Voisin’s recent proposal via constant cycle subvarieties, and prove a conjecture of hers on the existence of special algebraically coisotropic subvarieties for the moduli space.
- Type
- Research Article
- Information
- Copyright
- © The Authors 2019
References
- 9
- Cited by


