Hostname: page-component-5cf477f64f-bmd9x Total loading time: 0 Render date: 2025-04-07T04:25:56.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Dense clusters of primes in subsets

Part of: Multiplicative number theory

Published online by Cambridge University Press:  01 April 2016

James Maynard
James Maynard*
Affiliation:
Centre de recherches mathématiques, Université de Montréal, Pavillon André-Aisenstadt, 2920 Chemin de la tour, Room 5357, Montréal (Québec), Canada H3T 1J4 email [email protected] Current address:Mathematical Institute, Radcliffe Observatory Quarter, Woodstock Road, Oxford, OX1 6GG, UK
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

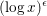We prove a generalization of the author’s work to show that any subset of the primes which is ‘well distributed’ in arithmetic progressions contains many primes which are close together. Moreover, our bounds hold with some uniformity in the parameters. As applications, we show there are infinitely many intervals of length $(\log x)^{{\it\epsilon}}$ containing 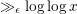$\gg _{{\it\epsilon}}\log \log x$ primes, and show lower bounds of the correct order of magnitude for the number of strings of 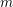$m$ congruent primes with 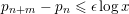$p_{n+m}-p_{n}\leqslant {\it\epsilon}\log x$.

Keywords

prime numberssieve methods

MSC classification

Primary: 11N05: Distribution of primes 11N35: Sieves
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 7 , July 2016 , pp. 1517 - 1554
Copyright
© The Author 2016 

References

Banks, W. D., Freiberg, T. and Turnage-Butterbaugh, C., Consecutive primes in tuples , Acta Arith. 167 (2015), 261–266.CrossRefGoogle Scholar
Benatar, J., The existence of small prime gaps in subsets of the integers, Preprint (2013), arXiv:1305.0348 [math.NT].Google Scholar
Castillo, A., Hall, C., Lemke Oliver, R., Pollack, P. and Thompson, L., Bounded gaps between primes in number fields and function fields , Proc. Amer. Math. Soc. 143 (2015), 2841–2856.Google Scholar
Davenport, H., Multiplicative number theory, Graduate Texts in Mathematics, vol. 74, third edition (Springer, New York, 2000), revised and with a preface by Hugh L. Montgomery.Google Scholar
Freiberg, T., Strings of congruent primes in short intervals , J. Lond. Math. Soc. (2) 84 (2011), 344–364.CrossRefGoogle Scholar
Goldston, D. A., Graham, S. W., Pintz, J. and Yıldırım, C. Y., Small gaps between products of two primes , Proc. Lond. Math. Soc. (3) 98 (2009), 741–774.Google Scholar
Goldston, D. A., Pintz, J. and Yıldırım, C. Y., Primes in tuples. I , Ann. of Math. (2) 170 (2009), 819–862.CrossRefGoogle Scholar
Goldston, D. A., Pintz, J. and Yıldırım, C. Y., Positive proportion of small gaps between consecutive primes , Publ. Math. Debrecen 79 (2011), 433–444.CrossRefGoogle Scholar
Harman, G., Watt, N. and Wong, K., A new mean-value result for Dirichlet L-functions and polynomials , Q. J. Math. 55 (2004), 307–324.CrossRefGoogle Scholar
Huxley, M. N. and Iwaniec, H., Bombieri’s theorem in short intervals , Mathematika 22 (1975), 188–194.Google Scholar
Knapowski, S. and Turán, P., On prime numbers ≡ 1 resp. 3 mod 4 , in Number theory and algebra (Academic Press, New York, 1977), 157–165.Google Scholar
Kumchev, A., The difference between consecutive primes in an arithmetic progression , Q. J. Math. 53 (2002), 479–501.Google Scholar
Li, H. and Pan, H., Bounded gaps between primes of the special form, Preprint (2014), arXiv:1403.4527 [math.NT].Google Scholar
Maynard, J., Small gaps between primes , Ann. of Math. (2) 181 (2015), 383–413.CrossRefGoogle Scholar
Murty, M. R. and Murty, V. K., A variant of the Bombieri–Vinogradov theorem , in Number theory (Montreal, Quebec, 1985), CMS Conference Proceedings, vol. 7 (American Mathematical Society, Providence, RI, 1987), 243–272.Google Scholar
Perelli, A., Pintz, J. and Salerno, S., Bombieri’s theorem in short intervals II , Invent. Math. 79 (1985), 1–9.CrossRefGoogle Scholar
Pollack, P., Bounded gaps between primes with a given primitive root , Algebra Number Theory 8 (2014), 1769–1786.CrossRefGoogle Scholar
Shiu, D. K. L., Strings of congruent primes , J. Lond. Math. Soc. (2) 61 (2000), 359–373.Google Scholar
Thorner, J., Bounded gaps between primes in Chebotarev sets , Res. Math. Sci. 1 (2014), doi:10.1186/2197-9847-1-4.CrossRefGoogle Scholar
Timofeev, N. M., Distribution of arithmetic functions in short intervals in the mean with respect to progressions , Izv. Akad. Nauk SSSR Ser. Mat. 51 (1987), 341–362, 447.Google Scholar
Zhang, Y., Bounded gaps between primes , Ann. of Math. (2) 179 (2014), 1121–1174.Google Scholar