Article contents
Constructing elliptic curves from Galois representations
Published online by Cambridge University Press: 29 August 2018
Abstract
Given a non-isotrivial elliptic curve over an arithmetic surface, one obtains a lisse 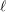 $\ell$-adic sheaf of rank two over the surface. This lisse sheaf has a number of straightforward properties: cyclotomic determinant, finite ramification, rational traces of Frobenius elements, and somewhere not potentially good reduction. We prove that any lisse sheaf of rank two possessing these properties comes from an elliptic curve.
$\ell$-adic sheaf of rank two over the surface. This lisse sheaf has a number of straightforward properties: cyclotomic determinant, finite ramification, rational traces of Frobenius elements, and somewhere not potentially good reduction. We prove that any lisse sheaf of rank two possessing these properties comes from an elliptic curve.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Authors 2018
Footnotes
AS was supported by NSF grants DMS-1303082 and DMS-1453893 and a Sloan Fellowship.
References
- 3
- Cited by


