Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T15:13:37.282Z Has data issue: false hasContentIssue false
  • English
  • Français

Constancy of generalized Hodge–Tate weights of a local system

Part of: Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  06 November 2018

Koji Shimizu
Koji Shimizu*
Affiliation:
Department of Mathematics, University of California, Berkeley, Evans Hall, Berkeley, CA 94720, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Sen attached to each 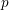$p$-adic Galois representation of a 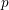$p$-adic field a multiset of numbers called generalized Hodge–Tate weights. In this paper, we discuss a rigidity of these numbers in a geometric family. More precisely, we consider a 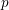$p$-adic local system on a rigid analytic variety over a 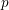$p$-adic field and show that the multiset of generalized Hodge–Tate weights of the local system is constant. The proof uses the 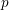$p$-adic Riemann–Hilbert correspondence by Liu and Zhu, a Sen–Fontaine decompletion theory in the relative setting, and the theory of formal connections. We also discuss basic properties of Hodge–Tate sheaves on a rigid analytic variety.

Keywords

rigid analytic geometryp-adic Hodge theory

MSC classification

Primary: 14G22: Rigid analytic geometry
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 12 , December 2018 , pp. 2606 - 2642
Copyright
© The Author 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

André, Y. and Baldassarri, F., De Rham cohomology of differential modules on algebraic varieties, Progress in Mathematics, vol. 189 (Birkhäuser, Basel, 2001).Google Scholar
Andreatta, F. and Brinon, O., Surconvergence des représentations p-adiques: le cas relatif , Astérisque 319 (2008), 39–116; Représentations $p$ -adiques de groupes $p$ -adiques. I. Représentations galoisiennes et $(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6E4})$ -modules.Google Scholar
Andreatta, F. and Brinon, O., B dR -représentations dans le cas relatif , Ann. Sci. Éc. Norm. Supér. (4) 43 (2010), 279–339.Google Scholar
Abbes, A., Gros, M. and Tsuji, T., The p-adic Simpson correspondence, Annals of Mathematics Studies, vol. 193 (Princeton University Press, Princeton, NJ, 2016).Google Scholar
Berger, L. and Colmez, P., Familles de représentations de de Rham et monodromie p-adique , Astérisque 319 (2008), 303–337; Représentations $p$ -adiques de groupes $p$ -adiques. I. Représentations galoisiennes et $(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6E4})$ -modules.Google Scholar
Brinon, O. and Conrad, B., CMI summer school notes on  $p$ -adic Hodge theory (preliminary version), available at http://math.stanford.edu/∼conrad/papers/notes.pdf, 2009.Google Scholar
Bellovin, R., p-adic Hodge theory in rigid analytic families , Algebra Number Theory 9 (2015), 371–433.Google Scholar
Berger, L., Représentations p-adiques et équations différentielles , Invent. Math. 148 (2002), 219–284.Google Scholar
Bosch, S., Güntzer, U. and Remmert, R., Non-Archimedean analysis, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 261 (Springer, Berlin, 1984); A systematic approach to rigid analytic geometry.Google Scholar
Bhatt, B., Morrow, M. and Scholze, P., Integral  $p$ -adic Hodge theory. Preprint (2018),arXiv:1602.03148v2.Google Scholar
Brinon, O., Une généralisation de la théorie de Sen , Math. Ann. 327 (2003), 793–813.Google Scholar
Chenevier, G., Une application des variétés de Hecke des groups unitaires, available athttp://gaetan.chenevier.perso.math.cnrs.fr/articles/famgal.pdf, 2009.Google Scholar
Colmez, P., Espaces vectoriels de dimension finie et représentations de de Rham , Astérisque 319 (2008), 117–186; Représentations $p$ -adiques de groupes $p$ -adiques. I. Représentations galoisiennes et $(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6E4})$ -modules.Google Scholar
Deligne, P., Équations différentielles à points singuliers réguliers, Lecture Notes in Mathematics, vol. 163 (Springer, Berlin–New York, 1970).Google Scholar
Dwork, B., Gerotto, G. and Sullivan, F. J., An introduction to G-functions, Annals of Mathematics Studies, vol. 133 (Princeton University Press, Princeton, NJ, 1994).Google Scholar
Faltings, G., A p-adic Simpson correspondence , Adv. Math. 198 (2005), 847–862.Google Scholar
Fontaine, J.-M., Arithmétique des représentations galoisiennes p-adiques , Astérisque 295 (2004), 1–115; Cohomologies $p$ -adiques et applications arithmétiques. III.Google Scholar
Huber, R., A generalization of formal schemes and rigid analytic varieties , Math. Z. 217 (1994), 513–551.Google Scholar
Huber, R., Étale cohomology of rigid analytic varieties and adic spaces, Aspects of Mathematics, E30 (Friedr. Vieweg & Sohn, Braunschweig, 1996).Google Scholar
Hyodo, O., On the Hodge–Tate decomposition in the imperfect residue field case , J. Reine Angew. Math. 365 (1986), 97–113.Google Scholar
Kedlaya, K. S. and Liu, R., Relative p-adic Hodge theory: foundations , Astérisque 371 (2015).Google Scholar
Kedlaya, K. S. and Liu, R., Relative p-adic Hodge theory, II: Imperfect period rings. Preprint (2016), arXiv:1602.06899v2.Google Scholar
Liu, R. and Zhu, X., Rigidity and a Riemann-Hilbert correspondence for p-adic local systems , Invent. Math. 207 (2017), 291–343.Google Scholar
Matsumura, H., Commutative ring theory, Cambridge Studies in Advanced Mathematics, vol. 8, second edition (Cambridge University Press, Cambridge, 1989); translated from the Japanese by M. Reid.Google Scholar
Scholze, P., Perfectoid spaces , Publ. Math. Inst. Hautes Études Sci. 116 (2012), 245–313.Google Scholar
Scholze, P., p-adic Hodge theory for rigid-analytic varieties , Forum Math. 1 (2013), e1, 77.Google Scholar
Scholze, P., p-adic Hodge theory for rigid-analytic varieties, Corrigendum , Forum Math. 4 (2016), e6, 4.Google Scholar
Sen, S., Continuous cohomology and p-adic Galois representations , Invent. Math. 62 (1980/81), 89–116.Google Scholar
Sen, S., The analytic variation of p-adic Hodge structure , Ann. of Math. (2) 127 (1988), 647–661.Google Scholar
Sen, S., An infinite-dimensional Hodge–Tate theory , Bull. Soc. Math. France 121 (1993), 13–34.Google Scholar
Scholze, P. and Weinstein, J., Berkeley lectures on  $p$ -adic geometry, available athttp://www.math.uni-bonn.de/people/scholze/Berkeley.pdf, 2018.Google Scholar
Tate, J. T., p-divisible groups , in Proc. conf. local fields (Driebergen, 1966) (Springer, Berlin, 1967), 158–183.Google Scholar
Tsuji, T., Purity for Hodge–Tate representations , Math. Ann. 350 (2011), 829–866.Google Scholar
Tsuji, T., Notes on the local p-adic Simpson correspondence , Math. Ann. 371 (2018), 795–881.Google Scholar