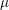Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T01:35:19.044Z Has data issue: false hasContentIssue false
  • English
  • Français

Congruences with Eisenstein series and $\unicode[STIX]{x1D707}$-invariants

Part of: Algebraic number theory: global fields Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  10 April 2019

Joël Bellaïche  and
Robert Pollack
Joël Bellaïche
Affiliation:
Department of Mathematics, Brandeis University, 415 South Street, Waltham, MA 02453, USA email [email protected]
Robert Pollack
Affiliation:
Department of Mathematics and Statistics, Boston University, 111 Cummington Mall, Boston, MA 02215, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the variation of 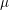$\unicode[STIX]{x1D707}$-invariants in Hida families with residually reducible Galois representations. We prove a lower bound for these invariants which is often expressible in terms of the 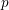$p$-adic zeta function. This lower bound forces these 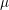$\unicode[STIX]{x1D707}$-invariants to be unbounded along the family, and we conjecture that this lower bound is an equality. When 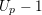$U_{p}-1$ generates the cuspidal Eisenstein ideal, we establish this conjecture and further prove that the 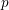$p$-adic 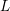$L$-function is simply a power of 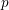$p$ up to a unit (i.e. 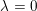$\unicode[STIX]{x1D706}=0$). On the algebraic side, we prove analogous statements for the associated Selmer groups which, in particular, establishes the main conjecture for such forms.

Keywords

Iwasawa theoryHida theory𝜇-invariantsresidually reducible

MSC classification

Primary: 11R23: Iwasawa theory 11F33: Congruences for modular and $p$-adic modular forms
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 5 , May 2019 , pp. 863 - 901
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ash, A. and Stevens, G., Modular forms in characteristic l and special values of their L-functions , Duke Math. J. 53 (1986), 849–868.10.1215/S0012-7094-86-05346-9Google Scholar
Bellaïche, J., Ribet’s lemma, generalizations, and pseudocharacters, Preprint (2009),http://people.brandeis.edu/∼jbellaic/RibetHawaii3.pdf.Google Scholar
Bellaïche, J., Critical p-adic L-functions , Invent. Math. 189 (2012), 1–60.Google Scholar
Bellaïche, J. and Dasgupta, S., The p-adic L-functions of evil Eisenstein series , Compos. Math. 151 (2015), 999–1040.Google Scholar
Colmez, P., Fonctions L p-adiques , in Séminaire Bourbaki, Vol. 1998/99, Exp. No. 851, Astérisque, vol. 266 (Société Mathématique de France, 2000), 3, 21–58.Google Scholar
Emerton, M., Pollack, R. and Weston, T., Variation of Iwasawa invariants in Hida families , Invent. Math. 163 (2006), 523–580.Google Scholar
Ferrero, B. and Washington, L. C., The Iwasawa invariant 𝜇 p vanishes for abelian number fields , Ann. of Math. (2) 109 (1979), 377–395.10.2307/1971116Google Scholar
Fukaya, T. and Kato, K., On conjectures of Sharifi, Preprint (2012),http://math.ucla.edu/∼sharifi/sharificonj.pdf.Google Scholar
Greenberg, R., Iwasawa theory for p-adic representations , in Algebraic number theory, Advanced Studies in Pure Mathematics, vol. 17 (Academic Press, Boston, 1989), 97–137.Google Scholar
Greenberg, R., Iwasawa theory for elliptic curves , in Arithmetic theory of elliptic curves (Cetraro, 1997), Lecture Notes in Mathematics, vol. 1716 (Springer, Berlin, 1999), 51–144.Google Scholar
Greenberg, R. and Stevens, G., p-adic L-functions and p-adic periods of modular forms , Invent. Math. 111 (1993), 407–447.Google Scholar
Greenberg, R. and Vatsal, V., On the Iwasawa invariants of elliptic curves , Invent. Math. 142 (2000), 17–63.Google Scholar
Hart, W., Harvey, D. and Ong, W., Irregular primes to two billion , Math. Comput. 86 (2017), 3031–3049.10.1090/mcom/3211Google Scholar
Hida, H., Iwasawa modules attached to congruences of cusp forms , Ann. Sci. Éc. Norm. Supér (4) 19 (1986), 231–273.Google Scholar
Hida, H., Geometric modular forms and elliptic curves, second edition (World Scientific, Hackensack, NJ, 2012).Google Scholar
Kato, K., p-adic Hodge theory and values of zeta functions of modular forms , in Cohomologies p-adiques et applications arithmétiques, III, Astérisque, vol. 295 (Société Mathématique de France, 2004), ix, 117–290.Google Scholar
Kitagawa, K., On standard p-adic L-functions of families of elliptic cusp forms , in p-adic monodromy and the Birch and Swinnerton–Dyer conjecture (Boston, MA, 1991), Contemporary Mathematics, vol. 165 (American Mathematical Society, Providence, RI, 1994), 81–110.Google Scholar
Kurihara, M., Ideal class groups of cyclotomic fields and modular forms of level 1 , J. Number Theory 45 (1993), 281–294.Google Scholar
Mahler, K., An interpolation series for continuous functions of a p-adic variable , J. Reine Angew. Math. 199 (1958), 23–34.Google Scholar
Mazur, B., Modular curves and the Eisenstein ideal , Publ. Math. Inst. Hautes Études Sci. (1978), 33–186, 1977.Google Scholar
Ohta, M., Ordinary p-adic étale cohomology groups attached to towers of elliptic modular curves , Compos. Math. 115 (1999), 241–301.Google Scholar
Ohta, M., Ordinary p-adic étale cohomology groups attached to towers of elliptic modular curves. II , Math. Ann. 318 (2000), 557–583.Google Scholar
Ohta, M., Congruence modules related to Eisenstein series , Ann. Sci. Éc. Norm. Supér. (4) 36 (2003), 225–269.Google Scholar
Ohta, M., Companion forms and the structure of p-adic Hecke algebras , J. Reine Angew. Math. 585 (2005), 141–172.Google Scholar
Pollack, R. and Stevens, G., Overconvergent modular symbols and p-adic L-functions , Ann. Sci. Éc. Norm. Supér. (4) 44 (2011), 1–42.Google Scholar
Pollack, R. and Stevens, G., Critical slope p-adic L-functions , J. Lond. Math. Soc. (2) 87 (2013), 428–452.Google Scholar
Ribet, K. A., A modular construction of unramified p-extensions of Q(𝜇 p ) , Invent. Math. 34 (1976), 151–162.Google Scholar
Sharifi, R., A reciprocity map and the two-variable p-adic L-function , Ann. of Math. (2) 173 (2011), 251–300.Google Scholar
Shimura, G., The special values of the zeta functions associated with cusp forms , Comm. Pure Appl. Math. 29 (1976), 783–804.Google Scholar
Skinner, C. and Urban, E., The Iwasawa main conjectures for GL2 , Invent. Math. 195 (2014), 1–277.10.1007/s00222-013-0448-1Google Scholar
Stevens, G., Rigid analytic modular symbols, Preprint (1994),http://math.bu.edu/people/ghs/preprints/OC-Symbs-04-94.pdf.Google Scholar
Tilouine, J., Hecke algebras and the Gorenstein property , in Modular forms and Fermat’s last theorem (Boston, MA, 1995) (Springer, New York, 1997), 327–342.10.1007/978-1-4612-1974-3_10Google Scholar
Vatsal, V., Canonical periods and congruence formulae , Duke Math. J. 98 (1999), 397–419.Google Scholar
Wake, P., Hecke algebras associated to 𝛬-adic modular forms , J. Reine Angew. Math. 700 (2015), 113–128.Google Scholar
Wiles, A., The Iwasawa conjecture for totally real fields , Ann. of Math. (2) 131 (1990), 493–540.Google Scholar
Wiles, A., Modular elliptic curves and Fermat’s last theorem , Ann. of Math. (2) 141 (1995), 443–551.Google Scholar