Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T02:03:58.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Cohomology of generalized configuration spaces

Part of: Homology and cohomology theories Homotopy theory Singularities Ordered sets Fiber spaces and bundles

Published online by Cambridge University Press:  20 December 2019

Dan Petersen
Dan Petersen*
Affiliation:
Matematiska Institutionen, Stockholms Universitet, 106 91Stockholm, Sweden email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 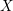$X$ be a topological space. We consider certain generalized configuration spaces of points on 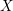$X$, obtained from the cartesian product 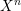$X^{n}$ by removing some intersections of diagonals. We give a systematic framework for studying the cohomology of such spaces using what we call ‘twisted commutative dg algebra models’ for the cochains on 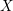$X$. Suppose that 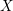$X$ is a ‘nice’ topological space, 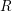$R$ is any commutative ring, 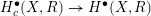$H_{c}^{\bullet }(X,R)\rightarrow H^{\bullet }(X,R)$ is the zero map, and that 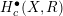$H_{c}^{\bullet }(X,R)$ is a projective 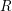$R$-module. We prove that the compact support cohomology of any generalized configuration space of points on 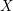$X$ depends only on the graded 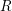$R$-module 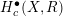$H_{c}^{\bullet }(X,R)$. This generalizes a theorem of Arabia.

Keywords

configuration spacesarrangementscohomology with compact support

MSC classification

Primary: 55R80: Discriminantal varieties, configuration spaces 32S60: Stratifications; constructible sheaves; intersection cohomology 55N30: Sheaf cohomology 06A07: Combinatorics of partially ordered sets 55P48: Loop space machines, operads
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 2 , February 2020 , pp. 251 - 298
Copyright
© The Author 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author gratefully acknowledges support by ERC-2017-STG 759082.

References

Aouina, M. and Klein, J. R., On the homotopy invariance of configuration spaces, Algebr. Geom. Topol. 4 (2004), 813–827.CrossRefGoogle Scholar
Arabia, A., Espaces de configuration généralisés. Espaces topologiques i-acycliques. Suites spectrales ‘basiques’, Preprint (2016), arXiv:1609.00522.Google Scholar
Arone, G., A generalization of Snaith-type filtration, Trans. Amer. Math. Soc. 351 (1999), 1123–1150.CrossRefGoogle Scholar
Arone, G. and Ching, M., Operads and chain rules for the calculus of functors, Astérisque 338 (2011).Google Scholar
Bacławski, K., Whitney numbers of geometric lattices, Adv. Math. 16 (1975), 125–138.CrossRefGoogle Scholar
Baranovsky, V. and Sazdanovic, R., Graph homology and graph configuration spaces, J. Homotopy Relat. Struct. 7 (2012), 223–235.CrossRefGoogle Scholar
Barratt, M. G., Twisted Lie algebras, in Geometric applications of homotopy theory (Proc. Conf., Evanston, IL, 1977), II, Lecture Notes in Mathematics, vol. 658 (Springer, Berlin, 1978), 9–15.CrossRefGoogle Scholar
Bendersky, M. and Gitler, S., The cohomology of certain function spaces, Trans. Amer. Math. Soc. 326 (1991), 423–440.CrossRefGoogle Scholar
Berger, C. and Moerdijk, I., Axiomatic homotopy theory for operads, Comment. Math. Helv. 78 (2003), 805–831.CrossRefGoogle Scholar
Berglund, A., Homological perturbation theory for algebras over operads, Algebr. Geom. Topol. 14 (2014), 2511–2548.CrossRefGoogle Scholar
Bhatt, B. and Scholze, P., The pro-étale topology for schemes, Astérisque 369 (2015), 99–201.Google Scholar
Björner, A. and Welker, V., The homology of ‘k-equal’ manifolds and related partition lattices, Adv. Math. 110 (1995), 277–313.CrossRefGoogle Scholar
Bremner, M. and Dotsenko, V., Algebraic operads: an algorithmic companion (CRC Press, Boca Raton, FL, 2016).CrossRefGoogle Scholar
Campos, R., Idrissi, N., Lambrechts, P. and Willwacher, T., Configuration spaces of manifolds with boundary, Preprint (2018), arXiv:1802.00716.Google Scholar
Chataur, D. and Cirici, J., Sheaves of E-infinity algebras and applications to algebraic varieties and singular spaces, Preprint (2018), arXiv:1811.08642.Google Scholar
Ching, M., Bar constructions for topological operads and the Goodwillie derivatives of the identity, Geom. Topol. 9 (2005), 833–933.CrossRefGoogle Scholar
Cohen, F. R. and Taylor, L. R., Computations of Gel’fand-Fuks cohomology, the cohomology of function spaces, and the cohomology of configuration spaces, in Geometric applications of homotopy theory (Proc. Conf., Evanston, IL, 1977), I, Lecture Notes in Mathematics, vol. 657 (Springer, Berlin, 1978), 106–143.CrossRefGoogle Scholar
Dotsenko, V. and Khoroshkin, A., Gröbner bases for operads, Duke Math. J. 153 (2010), 363–396.CrossRefGoogle Scholar
Fresse, B., On the homotopy of simplicial algebras over an operad, Trans. Amer. Math. Soc. 352 (2000), 4113–4141.CrossRefGoogle Scholar
Fresse, B., Koszul duality of operads and homology of partition posets, in Homotopy theory: relations with algebraic geometry, group cohomology, and algebraic K-theory, Contemporary Mathematics, vol. 346 (American Mathematical Society, Providence, RI, 2004), 115–215.Google Scholar
Getzler, E., The homology groups of some two-step nilpotent Lie algebras associated to symplectic vector spaces, Preprint (1999), arXiv:math/9903147.Google Scholar
Getzler, E., Resolving mixed Hodge modules on configuration spaces, Duke Math. J. 96 (1999), 175–203.CrossRefGoogle Scholar
Getzler, E. and Jones, J. D. S., Operads, homotopy algebra and iterated integrals for double loop spaces, Preprint (1994), arXiv:math/9403055.Google Scholar
Goerss, P. and Schemmerhorn, K., Model categories and simplicial methods, in Interactions between homotopy theory and algebra, Contemporary Mathematics, vol. 436 (Providence, RI, 2007), 3–49.CrossRefGoogle Scholar
Goresky, M. and MacPherson, R., Stratified Morse theory, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), vol. 14 (Springer, Berlin, 1988).CrossRefGoogle Scholar
Harper, J. E., Homotopy theory of modules over operads and non-𝛴 operads in monoidal model categories, J. Pure Appl. Algebra 214 (2010), 1407–1434.CrossRefGoogle Scholar
Hinich, V., Homological algebra of homotopy algebras, Comm. Algebra 25 (1997), 3291–3323.CrossRefGoogle Scholar
Hô, Q. P., Free factorization algebras and homology of configuration spaces in algebraic geometry, Selecta Math. (N.S.) 23 (2017), 2437–2489.CrossRefGoogle Scholar
Hô, Q. P., Densities and stability via factorization homology, Preprint (2018), arXiv:1802.07948.Google Scholar
Hovey, M., Model categories, Mathematical Surveys and Monographs, vol. 63 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Iversen, B., Cohomology of sheaves, Universitext (Springer, Berlin, 1986).CrossRefGoogle Scholar
Joyal, A., Foncteurs analytiques et espèces de structures, in Combinatoire énumérative (Montreal, Que., 1985/Quebec, Que. 1985), Lecture Notes in Mathematics, vol. 1234 (Springer, Berlin, 1986), 126–159.CrossRefGoogle Scholar
Kadeishvili, T., Cohomology $C_{\infty }$-algebra and rational homotopy type, Preprint (2008),arXiv:0811.1655.Google Scholar
Kadeišvili, T. V., On the theory of homology of fiber spaces, Uspekhi. Mat. Nauk 35 (1980), 183–188; International Topology Conference (Moscow State University, Moscow, 1979).Google Scholar
Knudsen, B., Betti numbers and stability for configuration spaces via factorization homology, Algebr. Geom. Topol. 17 (2017), 3137–3187.CrossRefGoogle Scholar
Knudsen, B., Higher enveloping algebras, Geom. Topol. 22 (2018), 4013–4066.CrossRefGoogle Scholar
Kozlov, D. N., General lexicographic shellability and orbit arrangements, Ann. Comb. 1 (1997), 67–90.CrossRefGoogle Scholar
Kříž, I., On the rational homotopy type of configuration spaces, Ann. of Math. (2) 139 (1994), 227–237.CrossRefGoogle Scholar
Loday, J.-L. and Vallette, B., Algebraic operads, Grundlehren der Mathematischen Wissenschaften, vol. 346 (Springer, Berlin, 2012).CrossRefGoogle Scholar
Mandell, M. A., Cochain multiplications, Amer. J. Math. 124 (2002), 547–566.CrossRefGoogle Scholar
Mandell, M. A., Cochains and homotopy type, Publ. Math. Inst. Hautes Études Sci. 103 (2006), 213–246.CrossRefGoogle Scholar
Navarro Aznar, V., Sur la théorie de Hodge–Deligne, Invent. Math. 90 (1987), 11–76.CrossRefGoogle Scholar
Pavlov, D. and Scholbach, J., Symmetric operads in abstract symmetric spectra, J. Inst. Math. Jussieu 18 (2018), 707–758.CrossRefGoogle Scholar
Petersen, D., A spectral sequence for stratified spaces and configuration spaces of points, Geom. Topol. 21 (2017), 2527–2555.CrossRefGoogle Scholar
Petersen, D., A closer look at Kadeishvili’s theorem, Preprint (2019), arXiv:1905.10877.Google Scholar
Quillen, D., Rational homotopy theory, Ann. of Math. (2) 90 (1969), 205–295.CrossRefGoogle Scholar
Richter, B., On the homology and homotopy of commutative shuffle algebras, Israel J. Math. 209 (2015), 651–682.CrossRefGoogle Scholar
Richter, B. and Sagave, S., A strictly commutative model for the cochain algebra of a space, Preprint (2018) arXiv:1801.01060.Google Scholar
Richter, B. and Shipley, B., An algebraic model for commutative Hℤ-algebras, Algebr. Geom. Topol. 17 (2017), 2013–2038.CrossRefGoogle Scholar
Ronco, M., Shuffle bialgebras, Ann. Inst. Fourier (Grenoble) 61 (2011), 799–850.CrossRefGoogle Scholar
Saleh, B., Noncommutative formality implies commutative and Lie formality, Algebr. Geom. Topol. 17 (2017), 2523–2542.CrossRefGoogle Scholar
Sagave, S. and Schlichtkrull, C., Diagram spaces and symmetric spectra, Adv. Math. 231 (2012), 2116–2193.CrossRefGoogle Scholar
Sam, S. V. and Snowden, A., Stability patterns in representation theory, Forum Math. Sigma 3 (2015), e11.CrossRefGoogle Scholar
Stover, C. R., The equivalence of certain categories of twisted Lie and Hopf algebras over a commutative ring, J. Pure Appl. Algebra 86 (1993), 289–326.CrossRefGoogle Scholar
Sullivan, D., Infinitesimal computations in topology, Publ. Math. Inst. Hautes Études Sci. 47 (1977), 269–331.CrossRefGoogle Scholar
Sundaram, S. and Wachs, M., The homology representations of the k-equal partition lattice, Trans. Amer. Math. Soc. 349 (1997), 935–954.CrossRefGoogle Scholar
Sundaram, S. and Welker, V., Group actions on arrangements of linear subspaces and applications to configuration spaces, Trans. Amer. Math. Soc. 349 (1997), 1389–1420.CrossRefGoogle Scholar
Tosteson, P., Lattice spectral sequences and cohomology of configuration spaces, Preprint (2016), arXiv:1612.06034.Google Scholar
Totaro, B., Configuration spaces of algebraic varieties, Topology 35 (1996), 1057–1067.CrossRefGoogle Scholar
Weibel, C. A., An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, vol. 38 (Cambridge University Press, Cambridge, 1994).CrossRefGoogle Scholar