Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T19:00:08.740Z Has data issue: false hasContentIssue false
  • English
  • Français

Cluster algebras and continued fractions

Part of: Arithmetic rings and other special rings Elementary number theory Series expansions

Published online by Cambridge University Press:  22 December 2017

İlke Çanakçı  and
Ralf Schiffler
İlke Çanakçı
Affiliation:
Department of Mathematical Sciences, Durham University, Lower Mountjoy, Stockton Road, Durham DH1 3LE, UK email [email protected]
Ralf Schiffler
Affiliation:
Department of Mathematics, University of Connecticut, Storrs, CT 06269-3009, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

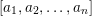We establish a combinatorial realization of continued fractions as quotients of cardinalities of sets. These sets are sets of perfect matchings of certain graphs, the snake graphs, that appear naturally in the theory of cluster algebras. To a continued fraction $[a_{1},a_{2},\ldots ,a_{n}]$ we associate a snake graph 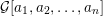${\mathcal{G}}[a_{1},a_{2},\ldots ,a_{n}]$ such that the continued fraction is the quotient of the number of perfect matchings of 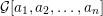${\mathcal{G}}[a_{1},a_{2},\ldots ,a_{n}]$ and 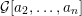${\mathcal{G}}[a_{2},\ldots ,a_{n}]$. We also show that snake graphs are in bijection with continued fractions. We then apply this connection between cluster algebras and continued fractions in two directions. First we use results from snake graph calculus to obtain new identities for the continuants of continued fractions. Then we apply the machinery of continued fractions to cluster algebras and obtain explicit direct formulas for quotients of elements of the cluster algebra as continued fractions of Laurent polynomials in the initial variables. Building on this formula, and using classical methods for infinite periodic continued fractions, we also study the asymptotic behavior of quotients of elements of the cluster algebra.

Keywords

cluster algebrascontinued fractionssnake graphs

MSC classification

Primary: 13F60: Cluster algebras
Secondary: 11A55: Continued fractions 30B70: Continued fractions
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 3 , March 2018 , pp. 565 - 593
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aigner, M., Markov’s theorem and 100 years of the uniqueness conjecture , in A mathematical journey from irrational numbers to perfect matchings (Springer, Cham, 2013).Google Scholar
Baur, K., Faber, E., Gratz, S., Serhiyenko, K. and Todorov, G., Mutation of friezes, Preprint (2016), arXiv:1612.05374.Google Scholar
Brüstle, T. and Zhang, J., On the cluster category of a marked surface without punctures , Algebra Number Theory 5 (2011), 529–566.Google Scholar
Çanakçı, İ. and Felikson, A., Infinite rank surface cluster algebras, Preprint (2017),arXiv:1704.01826.Google Scholar
Çanakçı, İ. and Schiffler, R., Snake graph calculus and cluster algebras from surfaces , J. Algebra 382 (2013), 240–281.Google Scholar
Çanakçı, İ. and Schiffler, R., Snake graph calculus and cluster algebras from surfaces II: self-crossing snake graphs , Math. Z. 281 (2015), 55–102.Google Scholar
Çanakçı, İ. and Schiffler, R., Snake graphs and continued fractions, Preprint (2017), arXiv:1711.02461.Google Scholar
Çanakçı, İ. and Schiffler, R., Snake graph calculus and cluster algebras from surfaces III: band graphs and snake rings , Int. Math. Res. Not. IMRN (2017), doi:10.1093/imrn/rnx157.Google Scholar
Coxeter, H. S. M., Frieze patterns , Acta Arith. 18 (1971), 298–310.CrossRefGoogle Scholar
Di Francesco, P. and Kedem, R., Q-systems, heaps, paths and cluster positivity , Comm. Math. Phys. 293 (2010), 727–802.Google Scholar
Fomin, S., Shapiro, M. and Thurston, D., Cluster algebras and triangulated surfaces. Part I: cluster complexes , Acta Math. 201 (2008), 83–146.Google Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras I: foundations , J. Amer. Math. Soc. 15 (2002), 497–529.Google Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras IV: coefficients , Compos. Math. 143 (2007), 112–164.Google Scholar
Grabowski, J. and Gratz, S., Cluster algebras of infinite rank , J. Lond. Math. Soc. (2) 89 (2014), 337–363.Google Scholar
Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers, fourth edition (Clarendon Press, Oxford, 1960).Google Scholar
Holm, T. and Jorgensen, P., On a cluster category of infinite Dynkin type, and the relation to triangulations of the infinity-gon , Math. Z. 270 (2012), 277–295.Google Scholar
Igusa, K. and Todorov, G., Continuous cluster categories I , Algebr. Represent. Theory 18 (2015), 65–101.Google Scholar
Labardini-Fragoso, D., Quivers with potentials associated to triangulated surfaces, part IV: removing boundary assumptions , Selecta Math. (N.S.) 22 (2016), 145–189.Google Scholar
Lee, K. and Schiffler, R., Positivity for cluster algebras , Ann. of Math. (2) 182 (2015), 73–125.Google Scholar
Liu, S. and Paquette, C., Cluster categories of type A ∞ ∞ and triangulations of the infinite strip , Math. Z. 286 (2017), 197–222.Google Scholar
Muir, T., A treatise on the theory of determinants (Dover, New York, 1960), revised and enlarged by William H. Metzler.Google Scholar
Musiker, G. and Schiffler, R., Cluster expansion formulas and perfect matchings , J. Algebraic Combin. 32 (2010), 187–209.CrossRefGoogle Scholar
Musiker, G., Schiffler, R. and Williams, L., Positivity for cluster algebras from surfaces , Adv. Math. 227 (2011), 2241–2308.Google Scholar
Musiker, G., Schiffler, R. and Williams, L., Bases for cluster algebras from surfaces , Compos. Math. 149 (2013), 217–263.Google Scholar
Nakanishi, T. and Stella, S., Wonder of sine-Gordon Y-systems , Trans. Amer. Math. Soc. 368 (2016), 6835–6886.Google Scholar
Palu, Y., Cluster characters for 2-Calabi-Yau triangulated categories , Ann. Inst. Fourier (Grenoble) 58 (2008), 2221–2248.CrossRefGoogle Scholar
Perron, O., Die Lehre von den Kettenbrüchen, second edition (Chelsea Publishing Company, New York, 1950). The first edition of this book from 1913 is available at https://archive.org/details/dielehrevondenk00perrgoog.Google Scholar
Propp, J., The combinatorics of frieze patterns and Markoff numbers, Preprint (2005), arXiv:0511633.Google Scholar
Qiu, Y. and Zhou, Y., Cluster categories for marked surfaces: punctured case , Compos. Math. 153 (2017), 1779–1819.Google Scholar
Schiffler, R., Lecture notes on cluster algebras from surfaces , in Homological methods, representation theory and cluster algebras: Proceedings of the CIMPA School, Mar del Plata, 2016, CRM Short Courses, eds Assem, I. and Trepode, S. (Springer), to appear.Google Scholar
Ustinov, A. V., A short proof of Euler’s identity for continuants , Mat. Zametki 79 (2006), 155–156 (Russian). Translation: Math. Notes 79 (2006), 146–147.Google Scholar