Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Johansson, Christian
2013.
Classicality for small slope overconvergent automorphic forms on some compact PEL Shimura varieties of type C.
Mathematische Annalen,
Vol. 357,
Issue. 1,
p.
51.
Di Matteo, Giovanni
2013.
On admissible tensor products inp-adic Hodge theory.
Compositio Mathematica,
Vol. 149,
Issue. 3,
p.
417.
Fourquaux, Lionel
and
Xie, Bingyong
2013.
Triangulable 𝒪F-analytic (φq,Γ)-modules of rank 2.
Algebra & Number Theory,
Vol. 7,
Issue. 10,
p.
2545.
Nakamura, Kentaro
2014.
Iwasawa theory of de Rham -modules over the Robba ring.
Journal of the Institute of Mathematics of Jussieu,
Vol. 13,
Issue. 1,
p.
65.
Kedlaya, Kiran
Pottharst, Jonathan
and
Xiao, Liang
2014.
Cohomology of arithmetic families of (𝜑,Γ)-modules.
Journal of the American Mathematical Society,
Vol. 27,
Issue. 4,
p.
1043.
DING, YIWEN
2016.
-INVARIANTS AND LOCAL–GLOBAL COMPATIBILITY FOR THE GROUP .
Forum of Mathematics, Sigma,
Vol. 4,
Issue. ,
Hellmann, Eugen
and
Schraen, Benjamin
2016.
Density of potentially crystalline representations of fixed weight.
Compositio Mathematica,
Vol. 152,
Issue. 8,
p.
1609.
Hansen, David
and
Newton, James
2017.
Universal eigenvarieties, trianguline Galois representations, and
p-adic Langlands functoriality.
Journal für die reine und angewandte Mathematik,
Vol. 2017,
Issue. 730,
p.
1.
Breuil, Christophe
Hellmann, Eugen
and
Schraen, Benjamin
2017.
Smoothness and classicality on Eigenvarieties.
Inventiones mathematicae,
Vol. 209,
Issue. 1,
p.
197.
Bergdall, John
2017.
Paraboline variation over -adic families of -modules.
Compositio Mathematica,
Vol. 153,
Issue. 1,
p.
132.
Le, Daniel
Morra, Stefano
and
Park, Chol
2018.
On mod p local-global compatibility for GL3(Qp) in the non-ordinary case.
Proceedings of the London Mathematical Society,
Vol. 117,
Issue. 4,
p.
790.
Breuil, Christophe
Hellmann, Eugen
and
Schraen, Benjamin
2019.
A local model for the trianguline variety and applications.
Publications mathématiques de l'IHÉS,
Vol. 130,
Issue. 1,
p.
299.
Berger, Laurent
and
Di Matteo, Giovanni
2021.
On triangulable tensor products of B-pairs and trianguline representations.
International Journal of Number Theory,
Vol. 17,
Issue. 10,
p.
2221.
Porat, Gal
2022.
Lubin–Tate theory and overconvergent Hilbert modular forms of low weight.
Israel Journal of Mathematics,
Vol. 249,
Issue. 1,
p.
431.
Wu, Zhixiang
2023.
Companion Points on the Eigenvariety with Non-Regular Weights.
International Mathematics Research Notices,
Vol. 2023,
Issue. 9,
p.
8008.
Poyeton, Léo
2023.
𝐹-analytic 𝐵-pairs.
Proceedings of the American Mathematical Society,
Breuil, Christophe
and
Ding, Yiwen
2023.
Sur un problème de compatibilité local-global localement analytique.
Memoirs of the American Mathematical Society,
Vol. 290,
Issue. 1442,
Wu, Ju-Feng
2024.
On Greenberg–Benois
$\mathcal {L}$
-invariants and Fontaine–Mazur
$\mathcal {L}$
-invariants.
Canadian Mathematical Bulletin,
Vol. 67,
Issue. 4,
p.
1141.
Breuil, Christophe
and
Ding, Yiwen
2024.
Bernstein Eigenvarieties.
Peking Mathematical Journal,
Vol. 7,
Issue. 2,
p.
471.


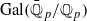 for
for 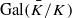 using
using 