Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T01:44:20.180Z Has data issue: false hasContentIssue false
  • English
  • Français

The classification of free algebras of orthogonal modular forms

Part of: Discontinuous groups and automorphic forms Metric geometry

Published online by Cambridge University Press:  06 August 2021

Haowu Wang
Haowu Wang*
Affiliation:
Max-Planck-Institut für Mathematik, Vivatsgasse 7, 53111Bonn, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a necessary and sufficient condition for the graded algebra of automorphic forms on a symmetric domain of type IV being free. From the necessary condition, we derive a classification result. Let 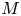$M$ be an even lattice of signature 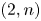$(2,n)$ splitting two hyperbolic planes. Suppose 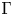$\Gamma$ is a subgroup of the integral orthogonal group of 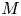$M$ containing the discriminant kernel. It is proved that there are exactly 26 groups 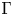$\Gamma$ such that the space of modular forms for 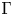$\Gamma$ is a free algebra. Using the sufficient condition, we recover some well-known results.

Keywords

modular forms for orthogonal groupssymmetric domains of type IVweighted projective spacesreflection groups

MSC classification

Primary: 11F55: Other groups and their modular and automorphic forms (several variables) 51F15: Reflection groups, reflection geometries 32N15: Automorphic functions in symmetric domains
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 9 , September 2021 , pp. 2026 - 2045
Copyright
© 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aoki, H. and Ibukiyama, T., Simple graded rings of Siegel modular forms, differential operators and Borcherds products, Internat. J. Math. 16 (2005), 249–279.CrossRefGoogle Scholar
Armstrong, M. A., The fundamental group of the orbit space of a discontinuous group, Math. Proc. Cambridge Philos. Soc. 64 (1968), 299–301.CrossRefGoogle Scholar
Baily, W. L. and Borel, A., Compactification of arithmetic quotients of bounded symmetric domains, Ann. of Math. (2) 84 (1966), 442–528.CrossRefGoogle Scholar
Borcherds, R. E., Automorphic forms on $\mathop { \mathrm {O}}\nolimits _{s+2, 2}$ and infinite products, Invent. Math. 120 (1995), 161–213.CrossRefGoogle Scholar
Borcherds, R. E., Automorphic forms with singularities on Grassmannians, Invent. Math. 123 (1998), 491–562.CrossRefGoogle Scholar
Borcherds, R. E., Reflection groups of Lorentzian lattices, Duke Math. J. 104 (2000), 319–366.CrossRefGoogle Scholar
Bourbaki, N., Groupes et algèbres de Lie, Chapters 4, 5 and 6 (Hermann, Paris, 1968).Google Scholar
Bruinier, J. H., Borcherds products on $\mathop { \mathrm {O}}\nolimits (2, n)$ and Chern classes of Heegner divisors, Lecture Notes in Mathematics, vol. 1780 (Springer, Berlin, 2002).Google Scholar
Bruinier, J. H., On the converse theorem for Borcherds products, J. Algebra 397 (2014), 315–342.CrossRefGoogle Scholar
Chevalley, C., Invariants of finite groups generated by reflections, Amer. J. Math. 77 (1955), 778–782.CrossRefGoogle Scholar
Cléry, F. and Gritsenko, V., Modular forms of orthogonal type and Jacobi theta-series, Abh. Math. Semin. Univ. Hambg. 83 (2013), 187–217.CrossRefGoogle Scholar
Dern, T. and Krieg, A., Graded rings of Hermitian modular forms of degree 2, Manuscripta Math. 110 (2003), 251–272.CrossRefGoogle Scholar
Dern, T. and Krieg, A., The graded ring of Hermitian modular forms of degree 2 over $\mathbb {Q}(\sqrt {-2} )$, J. Number Theory 107 (2004), 241–265.CrossRefGoogle Scholar
Dieckmann, C., Krieg, A. and Woitalla, M., The graded ring of modular forms on the Cayley half-space of degree two, Ramanujan J. 48 (2019), 385–398.CrossRefGoogle Scholar
Dittmann, M., Reflective automorphic forms on lattices of squarefree level, Trans. Amer. Math. Soc. 372 (2019), 1333–1362.CrossRefGoogle Scholar
Eichler, M. and Zagier, D., The theory of Jacobi forms, Progress in Mathematics, vol. 55 (Birkhäuser, Boston, MA, 1985.)CrossRefGoogle Scholar
Freitag, E. and Hermann, C. F., Some modular varieties of low dimension, Adv. Math. 152 (2000), 203–287.CrossRefGoogle Scholar
Freitag, E. and Salvati Manni, R., Some modular varieties of low dimension II, Adv. Math. 214 (2007), 132–145.CrossRefGoogle Scholar
Gritsenko, V., Reflective modular forms and their applications, Russian Math. Surveys 73 (2018), 797–864.CrossRefGoogle Scholar
Gritsenko, V., Hulek, K. and Sankaran, G. K., Abelianisation of orthogonal groups and the fundamental group of modular varieties, J. Algebra 322 (2009), 463–478.CrossRefGoogle Scholar
Gritsenko, V., Hulek, K. and Sankaran, G. K., Moduli of K3 surfaces and irreducible symplectic manifolds, in Handbook of moduli, Vol. I, eds G. Farkas and I. Morrison, Advanced Lectures in Mathematics, vol. 24 (International Press, Somerville, MA, 2013), 459–526.Google Scholar
Gritsenko, V. and Nikulin, V. V., Lorentzian Kac-Moody algebras with Weyl groups of $2$-reflections, Proc. Lond. Math. Soc. (3) 116 (2018), 485–533.CrossRefGoogle Scholar
Gottschling, E., Invarianten endlichen Gruppen und biholomorphe Abbildungen, Invent. Math. 6 (1969), 315–326.CrossRefGoogle Scholar
Gundlach, K. B., Die Bestimmung der Funktionen zur Hilbertschen Modulgruppe des Zahlkorpers $\mathbb {Q}(\sqrt {5})$, Math. Ann. 152 (1963), 226–256.CrossRefGoogle Scholar
Hashimoto, H. and Ueda, K., The ring of modular forms for the even unimodular lattice of signature $(2, 10)$, Proc. Amer. Math. Soc., to appear. Preprint (2014), arXiv:1406.0332.Google Scholar
Igusa, J., On Siegel modular forms of genus two, Amer. J. Math. 84 (1962), 175–200.CrossRefGoogle Scholar
Krieg, A., The graded ring of quaternionic modular forms of degree 2, Math. Z. 251 (2005), 929–944.CrossRefGoogle Scholar
Ma, S., Finiteness of $2$-reflective lattices of signature $(2, n)$, Amer. J. Math. 139 (2017), 513–524.CrossRefGoogle Scholar
Ma, S., On the Kodaira dimension of orthogonal modular varieties, Invent. Math. 212 (2018), 859–911.CrossRefGoogle Scholar
Nikulin, V. V., Integral symmetric bilinear forms and some of their applications, Math. USSR Izv. 14 (1980), 103–167.CrossRefGoogle Scholar
Platonov, V. and Rapinchuk, A., Algebraic groups and number theory, Pure and Applied Mathematics, vol. 139 (Academic Press, Boston, MA, 1994).CrossRefGoogle Scholar
Runge, B., On Siegel modular forms, I, J. Reine Angew. Math. 436 (1993), 57–85.Google Scholar
Scheithauer, N. R., On the classification of automorphic products and generalized Kac-Moody algebras, Invent. Math. 164 (2006), 641–678.CrossRefGoogle Scholar
Scheithauer, N. R., Automorphic products of singular weight, Compos. Math. 153 (2017), 1855–1892.CrossRefGoogle Scholar
Serre, J. P., A course in arithmetic, Graduate Texts in Mathematics, vol. 7 (Springer, New York, NY, 1973).CrossRefGoogle Scholar
Shephard, G. C. and Todd, J. A., Finite unitary reflection groups, Canad. J. Math. 6 (1954), 274–304.CrossRefGoogle Scholar
Shvartsman, O. V. and Vinberg, E. B., A criterion of smoothness at infinity for an arithmetic quotient of the future tube, Funktsional. Anal. i Prilohzen. 51 (2017), 40–59; Funct. Anal. Appl. 51 (2017), 32–47 (English translation).Google Scholar
Stuken, E. S., Free algebras of Hilbert automorphic forms, Funktsional. Anal. i Prilohzen. 53 (2019), 49–66; Funct. Anal. Appl. 53 (2019), 37–50 (English translation).Google Scholar
Vinberg, E. B., Some free algebras of automorphic forms on symmetric domains of type IV, Transform. Groups 15 (2010), 701–741.CrossRefGoogle Scholar
Vinberg, E. B., On the algebra of Siegel modular forms of genus 2, Tr. Mosk. Mat. Obshch. 74 (2013), 1–16; Trans. Moscow Math. Soc. 74 (2013), 1–13 (English translation).Google Scholar
Vinberg, E. B., On some free algebras of automorphic forms, Funktsional. Anal. i Prilohzen. 52 (2018), 38–61; Funct. Anal. Appl. 52 (2018), 270–289 (English translation).Google Scholar
Vinberg, E. B. and Popov, V. L., Invariant theory, in Algebraic Theory-4, Itogi Nauki i Tekhniki. Sovrem. Probl. Mat. Fund. Napr., vol. 55 (VINITI, Moscow, 1989), 137–309; Algebraic Geometry IV, Encyclopaedia of Mathematical Sciences, vol. 55, (Springer, Berlin), 123–278 (English translation).Google Scholar
Wang, H., Weyl invariant $E_8$ Jacobi forms, Commun. Number Theory Phys., to appear. Preprint (2018), arXiv:1801.08462.Google Scholar
Wang, H., The classification of $2$-reflective modular forms, Preprint (2019), arXiv:1906.10459.Google Scholar
Wang, H., Reflective modular forms: A Jacobi forms approach, Int. Math. Res. Not. IMRN 2021 (2021), 2081–2107.CrossRefGoogle Scholar
Wang, H. and Williams, B., On some free algebras of orthogonal modular forms, Adv. Math. 373 (2020), 107332, 22 pp.CrossRefGoogle Scholar
Woitalla, M., Theta type Jacobi forms, Acta Arith. 181 (2017), 333–354.CrossRefGoogle Scholar