Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T09:18:53.040Z Has data issue: false hasContentIssue false
  • English
  • Français

The Chowla–Selberg formula for abelian CM fields and Faltings heights

Part of: Arithmetic algebraic geometry Algebraic number theory: global fields Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  24 September 2015

Adrian Barquero-Sanchez  and
Riad Masri
Adrian Barquero-Sanchez
Affiliation:
Department of Mathematics, Mailstop 3368, Texas A&M University, College Station, TX 77843-3368, USA email [email protected]
Riad Masri
Affiliation:
Department of Mathematics, Mailstop 3368, Texas A&M University, College Station, TX 77843-3368, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we establish a Chowla–Selberg formula for abelian CM fields. This is an identity which relates values of a Hilbert modular function at CM points to values of Euler’s gamma function 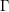${\rm\Gamma}$ and an analogous function 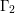${\rm\Gamma}_{2}$ at rational numbers. We combine this identity with work of Colmez to relate the CM values of the Hilbert modular function to Faltings heights of CM abelian varieties. We also give explicit formulas for products of exponentials of Faltings heights, allowing us to study some of their arithmetic properties using the Lang–Rohrlich conjecture.

Keywords

Chowla–Selberg formulaCM pointFaltings heightHilbert modular function

MSC classification

Primary: 11F41: Automorphic forms on $(2)$; Hilbert and Hilbert-Siegel modular groups and their modular and automorphic forms; Hilbert modular surfaces 11R42: Zeta functions and $L$-functions of number fields 11G50: Heights
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 3 , March 2016 , pp. 445 - 476
Copyright
© The Authors 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, G. W., Logarithmic derivatives of Dirichlet L-functions and the periods of abelian varieties, Compositio Math. 45 (1982), 315–332.Google Scholar
Anderson, G. W., Brownawell, D. W. and Papanikolas, M. A., Determination of the algebraic relations among special Γ-values in positive characteristic, Ann. of Math. (2) 160 (2004), 237–313.Google Scholar
Asai, T., On a certain function analogous to log|𝜂(z)|, Nagoya Math. J. 40 (1970), 193–211.Google Scholar
Bost, J.-B., Mestre, J.-F. and Moret-Bailly, L., Sur le calcul explicite des ‘classes de Chern’ des surfaces arithmétiques de genre 2 [On the explicit calculation of the ‘Chern classes’ of arithmetic surfaces of genus 2], in Séminaire sur les pinceaux de courbes elliptiques (Paris, 1988), Astérisque, vol. 183 (Société Mathématique de France, 1990), 69–105 (in French).Google Scholar
Bruinier, J. H., Kudla, S. S. and Yang, T. H., Special values of Green functions at big CM points, Int. Math. Res. Not. IMRN 9 (2012), 1917–1967.Google Scholar
Bruinier, J. H. and Yang, T. H., CM-values of Hilbert modular functions, Invent. Math. 163 (2006), 229–288.Google Scholar
Bruinier, J. H. and Yang, T. H., Twisted Borcherds products on Hilbert modular surfaces and their CM values, Amer. J. Math. 129 (2007), 807–841.Google Scholar
Bruinier, J. H. and Yang, T. H., CM values of automorphic Green functions on orthogonal groups over totally real fields, in Arithmetic geometry and automorphic forms, Advanced Lectures in Mathematics (ALM), vol. 19 (International Press, Somerville, MA, 2011), 1–54.Google Scholar
Chowla, S. and Selberg, A., On Epstein’s zeta function. I, Proc. Natl. Acad. Sci. USA 35 (1949), 371–374.Google Scholar
Chowla, S. and Selberg, A., On Epstein’s zeta-function, J. reine angew. Math. 227 (1967), 86–110.Google Scholar
Cohen, H., Number theory, in Analytic and modern tools, Vol. II, Graduate Texts in Mathematics, vol. 240 (Springer, New York, 2007).Google Scholar
Colmez, P., Périodes des variétés abéliennes à multiplication complexe, Ann. of Math. (2) 138 (1993), 625–683.Google Scholar
Conner, P. E. and Hurrelbrink, J., Class number parity, Series in Pure Mathematics, vol. 8 (World Scientific, Singapore, 1988).CrossRefGoogle Scholar
Deligne, P., Valeurs de fonctions L et périodes d’intégrales, in Automorphic forms, representations and L-functions (Oregon State University, Corvallis, OR, 1977), Part 2, Proceedings of Symposia in Pure Mathematics, vol. XXXIII (American Mathematical Society, Providence, RI, 1979), 313–346; with an appendix by N. Koblitz and A. Ogus.Google Scholar
Deninger, C., On the analogue of the formula of Chowla and Selberg for real quadratic fields, J. reine angew. Math. 351 (1984), 171–191.Google Scholar
Fröhlich, A., Central extensions, Galois groups, and ideal class groups of number fields, Contemporary Mathematics, vol. 24 (American Mathematical Society, Providence, RI, 1983).CrossRefGoogle Scholar
Gross, B. H., Arithmetic on elliptic curves with complex multiplication, Lecture Notes in Mathematics, vol. 776 (Springer, Berlin, 1980); with an appendix by B. Mazur.Google Scholar
Gross, B. H. and Zagier, D. B., On singular moduli, J. reine angew. Math. 355 (1985), 191–220.Google Scholar
Kato, K., Kurokawa, N. and Saito, T., Number theory. 2. Introduction to class field theory, Translations of Mathematical Monographs, vol. 240, Iwanami Series in Modern Mathematics (American Mathematical Society, Providence, RI, 2011); Translated from the 1998 Japanese original by Masato Kuwata and Katsumi Nomizu.Google Scholar
Lang, S., Cyclotomic fields I and II, Graduate Texts in Mathematics, vol. 121 (Springer, New York, 1990).Google Scholar
Lang, S., Algebraic number theory, Graduate Texts in Mathematics, vol. 110, second edition (Springer, New York, 1994).Google Scholar
Lerch, M., Sur quelques formules relatives au nombre des classes, Bull. Sci. Math. (2) 21 (1897), 302–303.Google Scholar
Masri, R., CM cycles and nonvanishing of class group L-functions, Math. Res. Lett. 17 (2010), 749–760.Google Scholar
Moreno, C. J., The Chowla–Selberg formula, J. Number Theory 17 (1983), 226–245.CrossRefGoogle Scholar
Mouhib, A., On the parity of the class number of multiquadratic number fields, J. Number Theory 129 (2009), 1205–1211.Google Scholar
Obus, A., On Colmez’s product formula for periods of CM-abelian varieties, Math. Ann. 356 (2013), 401–418.Google Scholar
Shintani, T., On evaluation of zeta functions of totally real algebraic number fields at non-positive integers, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 23 (1976), 393–417.Google Scholar
Shintani, T., On values at s = 1 of certain L functions of totally real algebraic number fields, in Algebraic number theory (Kyoto Int. Sympos., Res. Inst. Math. Sci., Univ. Kyoto, Kyoto, 1976) (Japan Society for the Promotion of Science, Tokyo, 1977), 201–212.Google Scholar
Silverman, J. H., Heights and elliptic curves, in Arithmetic geometry (Storrs, CT, 1984) (Springer, New York, 1986), 253–265.Google Scholar
van der Geer, G., Hilbert modular surfaces, in Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in mathematics and related areas (3)], Vol. 16 (Springer, Berlin, 1988).Google Scholar
Weil, A., Elliptic functions according to Eisenstein and Kronecker, in Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 88 (Springer, New York, 1976).Google Scholar
Yang, T. H., An arithmetic intersection formula on Hilbert modular surfaces, Amer. J. Math. 132 (2010), 1275–1309.Google Scholar
Yang, T. H., The Chowla–Selberg formula and the Colmez conjecture, Canad. J. Math. 62 (2010), 456–472.Google Scholar
Yang, T. H., Arithmetic intersection on a Hilbert modular surface and the Faltings height, Asian J. Math. 17 (2013), 335–381.Google Scholar
Yoshida, H., On absolute CM-periods, in Automorphic forms, automorphic representations, and arithmetic (Fort Worth, TX, 1996), Proceedings of Symposia in Pure Mathematics, vol. 66, Part 1 (American Mathematical Society, Providence, RI, 1999), 221–278.Google Scholar
Zagier, D., Elliptic modular forms and their applications, in The 1-2-3 of modular forms, Universitext (Springer, Berlin, 2008), 1–103.Google Scholar