Published online by Cambridge University Press: 31 March 2020
We prove that for each characteristic direction 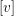 $[v]$ of a tangent to the identity diffeomorphism of order
$[v]$ of a tangent to the identity diffeomorphism of order 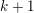 $k+1$ in
$k+1$ in 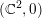 $(\mathbb{C}^{2},0)$ there exist either an analytic curve of fixed points tangent to
$(\mathbb{C}^{2},0)$ there exist either an analytic curve of fixed points tangent to 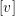 $[v]$ or
$[v]$ or 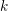 $k$ parabolic manifolds where all the orbits are tangent to
$k$ parabolic manifolds where all the orbits are tangent to 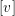 $[v]$, and that at least one of these parabolic manifolds is or contains a parabolic curve.
$[v]$, and that at least one of these parabolic manifolds is or contains a parabolic curve.
The first author was partially supported by Ministerio de Economía y Competitividad, Spain, process MTM2016-77642-C2-1-P; the second author was supported by Vicerrectorado de Investigación de la Pontificia Universidad Católica del Perú.