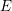Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-16T22:22:52.042Z Has data issue: false hasContentIssue false
  • English
  • Français

Brown–Peterson cohomology from Morava $E$-theory

Part of: Fiber spaces and bundles Homology and cohomology theories

Published online by Cambridge University Press:  13 March 2017

Tobias Barthel  and
Nathaniel Stapleton
Tobias Barthel
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, 2100 Køpenhavn Ø, Denmark email [email protected]
Nathaniel Stapleton
Affiliation:
Fakultät für Mathematik, Universität Regensburg, 93040 Regensburg, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that the 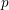$p$-completed Brown–Peterson spectrum is a retract of a product of Morava 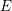$E$-theory spectra. As a consequence, we generalize results of Kashiwabara and of Ravenel, Wilson and Yagita from spaces to spectra and deduce that the notion of a good group is determined by Brown–Peterson cohomology. Furthermore, we show that rational factorizations of the Morava 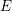$E$-theory of certain finite groups hold integrally up to bounded torsion with height-independent exponent, thereby lifting these factorizations to the rationalized Brown–Peterson cohomology of such groups.

Keywords

Brown–Peterson spectrumMorava E-theorytranschromatic character theory

MSC classification

Primary: 55N20: Generalized (extraordinary) homology and cohomology theories
Secondary: 55N22: Bordism and cobordism theories, formal group laws 55R40: Homology of classifying spaces, characteristic classes
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 4 , April 2017 , pp. 780 - 819
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ando, M., Hopkins, M. J. and Strickland, N. P., The sigma orientation is an H ∞ map , Amer. J. Math. 126 (2004), 247–334; MR 2045503 (2005d:55009).CrossRefGoogle Scholar
Barthel, T. and Frankland, M., Completed power operations for Morava E-theory , Algebr. Geom. Topol. 15 (2015), 2065–2131; MR 3402336.Google Scholar
Barthel, T. and Stapleton, N., Centralizers in good groups are good , Algebr. Geom. Topol. 16 (2016), 1453–1472.CrossRefGoogle Scholar
Bousfield, A. K., The localization of spectra with respect to homology , Topology 18 (1979), 257–281; MR 551009 (80m:55006).Google Scholar
Bousfield, A. K., Uniqueness of infinite deloopings for K-theoretic spaces , Pacific J. Math. 129 (1987), 1–31; MR 901254 (89g:55017).Google Scholar
Devinatz, E. S., Hopkins, M. J. and Smith, J. H., Nilpotence and stable homotopy theory. I , Ann. of Math. (2) 128 (1988), 207–241; MR 960945 (89m:55009).CrossRefGoogle Scholar
Drinfeld, V. G., Elliptic modules , Math. USSR Sb. 23 (1974), 561–592.Google Scholar
Dwyer, W. G. and Greenlees, J. P. C., Complete modules and torsion modules , Amer. J. Math. 124 (2002), 199–220; MR 1879003.Google Scholar
Elmendorf, A. D., Kriz, I., Mandell, M. A. and May, J. P., Rings, modules, and algebras in stable homotopy theory, Mathematical Surveys and Monographs, vol. 47 (American Mathematical Society, Providence, RI, 1997), with an appendix by M. Cole; MR 1417719 (97h:55006).Google Scholar
Greenlees, J. P. C. and Sadofsky, H., The Tate spectrum of v n -periodic complex oriented theories , Math. Z. 222 (1996), 391–405; MR 1400199 (97d:55010).Google Scholar
Hopkins, M., Complex oriented cohomology theories and the language of stacks, Course Notes,http://www.math.rochester.edu/people/faculty/doug/otherpapers/coctalos.pdf.Google Scholar
Hopkins, M. J., Kuhn, N. J. and Ravenel, D. C., Generalized group characters and complex oriented cohomology theories , J. Amer. Math. Soc. 13 (2000), 553–594.Google Scholar
Hopkins, M. J. and Smith, J. H., Nilpotence and stable homotopy theory. II , Ann. of Math. (2) 148 (1998), 1–49; MR 1652975 (99h:55009).Google Scholar
Hovey, M., Bousfield localization functors and Hopkins’ chromatic splitting conjecture , in The Čech centennial (Boston, MA, 1993), Contemporary Mathematics, vol. 181 (American Mathematical Society, Providence, RI, 1995), 225–250; MR 1320994 (96m:55010).Google Scholar
Hovey, M. A., v n -elements in ring spectra and applications to bordism theory , Duke Math. J. 88 (1997), 327–356; MR 1455523 (98d:55017).CrossRefGoogle Scholar
Hovey, M., Operations and co-operations in Morava E-theory , Homology, Homotopy Appl. 6 (2004), 201–236; MR 2076002 (2005f:55003).Google Scholar
Hovey, M., Some spectral sequences in Morava $E$ -theory, Preprint (2004).Google Scholar
Hovey, M. and Sadofsky, H., Invertible spectra in the E (n)-local stable homotopy category , J. Lond. Math. Soc. (2) 60 (1999), 284–302; MR 1722151 (2000h:55017).Google Scholar
Hovey, M. and Strickland, N. P., Morava K-theories and localisation , Mem. Amer. Math. Soc. 139 (1999), no. 666, viii+100pp; MR 1601906 (99b:55017).Google Scholar
Johnson, D. C. and Wilson, W. S., Projective dimension and Brown–Peterson homology , Topology 12 (1973), 327–353; MR 0334257 (48 #12576).Google Scholar
Johnson, D. C. and Wilson, W. S., BP operations and Morava’s extraordinary K-theories , Math. Z. 144 (1975), 55–75; MR 0377856 (51 #14025).Google Scholar
Kashiwabara, T., Brown–Peterson cohomology of 𝛺 ∞ 𝛴 ∞ S 2n , Quart. J. Math. 49 (1998), 345–362; MR 1645564 (2000d:55013).Google Scholar
Kashiwabara, T., On Brown–Peterson cohomology of QX , Ann. of Math. (2) 153 (2001), 297–328; MR 1829752 (2002f:55013).Google Scholar
Kono, A. and Yagita, N., Brown–Peterson and ordinary cohomology theories of classifying spaces for compact Lie groups , Trans. Amer. Math. Soc. 339 (1993), 781–798; MR 1139493 (93m:55006).Google Scholar
Kuhn, N. J., Morava K-theories and infinite loop spaces , in Algebraic topology (Arcata, CA, 1986), Lecture Notes in Mathematics, vol. 1370 (Springer, Berlin, 1989), 243–257; MR 1000381 (90d:55014).CrossRefGoogle Scholar
Kuhn, N. J., Localization of André–Quillen–Goodwillie towers, and the periodic homology of infinite loopspaces , Adv. Math. 201 (2006), 318–378; MR 2211532 (2007d:55006).CrossRefGoogle Scholar
Lam, T. Y., Lectures on modules and rings, Graduate Texts in Mathematics, vol. 189 (Springer, New York, 1999); MR 1653294 (99i:16001).Google Scholar
Landweber, P. S., Annihilator ideals and primitive elements in complex bordism , Illinois J. Math. 17 (1973), 273–284; MR 0322874 (48 #1235).Google Scholar
Landweber, P. S., Homological properties of comodules over MU ∗(MU) and BP ∗(BP) , Amer. J. Math. 98 (1976), 591–610; MR 0423332 (54 #11311).Google Scholar
Margolis, H. R., Modules over the Steenrod algebra and the stable homotopy category , in Spectra and the Steenrod algebra, North-Holland Mathematical Library, vol. 29 (North-Holland, Amsterdam, 1983); MR 738973 (86j:55001).Google Scholar
Minami, N., From K (n + 1)∗(X) to K (n)∗(X) , Proc. Amer. Math. Soc. 130 (2002), 1557–1562; MR 1879983 (2003a:55009).Google Scholar
Quillen, D., Elementary proofs of some results of cobordism theory using Steenrod operations , Adv. Math. 7 (1971), 29–56; MR 0290382.Google Scholar
Ravenel, D. C. and Wilson, W. S., The Morava K-theories of Eilenberg–MacLane spaces and the Conner–Floyd conjecture , Amer. J. Math. 102 (1980), 691–748; MR 584466 (81i:55005).Google Scholar
Ravenel, D. C., Wilson, W. S. and Yagita, N., Brown–Peterson cohomology from MoravaK-theory , K-Theory 15 (1998), 147–199; MR 1648284 (2000d:55012).Google Scholar
Rezk, C., The congruence criterion for power operations in Morava E-theory , Homology, Homotopy Appl. 11 (2009), 327–379; MR 2591924 (2011e:55021).Google Scholar
Rezk, C., Rings of power operations for Morava $E$ -theories are Koszul, Preprint (2012),arXiv:1204.4831.Google Scholar
Schlank, T. and Stapleton, N., A transchromatic proof of Strickland’s theorem , Adv. Math. 285 (2015), 1415–1447; MR 3406531.Google Scholar
Schuster, B. and Yagita, N., Transfers of Chern classes in BP-cohomology and Chow rings , Trans. Amer. Math. Soc. 353 (2001), 1039–1054; MR 1804412 (2002b:55030).CrossRefGoogle Scholar
Stapleton, N., Transchromatic generalized character maps , Algebr. Geom. Topol. 13 (2013), 171–203; MR 3031640.Google Scholar
Stapleton, N., Subgroups of p-divisible groups and centralizers in symmetric groups , Trans. Amer. Math. Soc. 367 (2015), 3733–3757; MR 3314822.Google Scholar
Strickland, N., Functorial philosophy for formal phenomena,http://hopf.math.purdue.edu/Strickland/fpfp.pdf.Google Scholar
Strickland, N. P., Finite subgroups of formal groups , J. Pure Appl. Algebra 121 (1997), 161–208; MR 1473889 (98k:14065).Google Scholar
Strickland, N. P., Formal schemes and formal groups , in Homotopy invariant algebraic structures (Baltimore, MD, 1998), Contemporary Mathematics, vol. 239 (American Mathematical Society, Providence, RI, 1999), 263–352; MR 1718087 (2000j:55011).Google Scholar
Wilson, W. S., Brown–Peterson cohomology from Morava K-theory. II , K-Theory 17 (1999), 95–101; MR 1696426 (2000d:55014).Google Scholar
Yagita, N., The exact functor theorem for BP ∗/I n -theory , Proc. Japan Acad. Ser. A Math. Sci. 52 (1976), 1–3; MR 0394631 (52 #15432).Google Scholar
Yosimura, Z.-i., Projective dimension of Brown–Peterson homology with modulo (p, v 1, …, v n-1) coefficients , Osaka J. Math. 13 (1976), 289–309; MR 0415603 (54 #3686).Google Scholar