Article contents
Braces and Poisson additivity
Published online by Cambridge University Press: 18 July 2018
Abstract
We relate the brace construction introduced by Calaque and Willwacher to an additivity functor. That is, we construct a functor from brace algebras associated to an operad 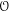 ${\mathcal{O}}$ to associative algebras in the category of homotopy
${\mathcal{O}}$ to associative algebras in the category of homotopy 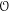 ${\mathcal{O}}$-algebras. As an example, we identify the category of
${\mathcal{O}}$-algebras. As an example, we identify the category of 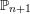 $\mathbb{P}_{n+1}$-algebras with the category of associative algebras in
$\mathbb{P}_{n+1}$-algebras with the category of associative algebras in 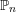 $\mathbb{P}_{n}$-algebras. We also show that under this identification there is an equivalence of two definitions of derived coisotropic structures in the literature.
$\mathbb{P}_{n}$-algebras. We also show that under this identification there is an equivalence of two definitions of derived coisotropic structures in the literature.
- Type
- Research Article
- Information
- Copyright
- © The Author 2018
Footnotes
Current address: Intitut für Mathematik, Winterthurerstrasse 190, 8057 Zürich, Switzerland
References
- 7
- Cited by


