Article contents
BPS invariants from p-adic integrals
Published online by Cambridge University Press: 30 May 2024
Abstract
We define 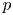 $p$-adic
$p$-adic 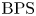 $\mathrm {BPS}$ or
$\mathrm {BPS}$ or 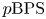 $p\mathrm {BPS}$ invariants for moduli spaces
$p\mathrm {BPS}$ invariants for moduli spaces 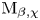 $\operatorname {M}_{\beta,\chi }$ of one-dimensional sheaves on del Pezzo and K3 surfaces by means of integration over a non-archimedean local field
$\operatorname {M}_{\beta,\chi }$ of one-dimensional sheaves on del Pezzo and K3 surfaces by means of integration over a non-archimedean local field 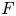 $F$. Our definition relies on a canonical measure
$F$. Our definition relies on a canonical measure 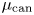 $\mu _{\rm can}$ on the
$\mu _{\rm can}$ on the 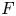 $F$-analytic manifold associated to
$F$-analytic manifold associated to 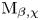 $\operatorname {M}_{\beta,\chi }$ and the
$\operatorname {M}_{\beta,\chi }$ and the 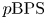 $p\mathrm {BPS}$ invariants are integrals of natural
$p\mathrm {BPS}$ invariants are integrals of natural 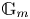 ${\mathbb {G}}_m$ gerbes with respect to
${\mathbb {G}}_m$ gerbes with respect to 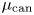 $\mu _{\rm can}$. A similar construction can be done for meromorphic and usual Higgs bundles on a curve. Our main theorem is a
$\mu _{\rm can}$. A similar construction can be done for meromorphic and usual Higgs bundles on a curve. Our main theorem is a 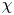 $\chi$-independence result for these
$\chi$-independence result for these 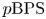 $p\mathrm {BPS}$ invariants. For one-dimensional sheaves on del Pezzo surfaces and meromorphic Higgs bundles, we obtain as a corollary the agreement of
$p\mathrm {BPS}$ invariants. For one-dimensional sheaves on del Pezzo surfaces and meromorphic Higgs bundles, we obtain as a corollary the agreement of 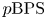 $p\mathrm {BPS}$ with usual
$p\mathrm {BPS}$ with usual 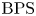 $\mathrm {BPS}$ invariants through a result of Maulik and Shen [Cohomological
$\mathrm {BPS}$ invariants through a result of Maulik and Shen [Cohomological 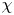 $\chi$-independence for moduli of one-dimensional sheaves and moduli of Higgs bundles, Geom. Topol. 27 (2023), 1539–1586].
$\chi$-independence for moduli of one-dimensional sheaves and moduli of Higgs bundles, Geom. Topol. 27 (2023), 1539–1586].
- Type
- Research Article
- Information
- Copyright
- © 2024 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
- 2
- Cited by



