Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T14:45:14.622Z Has data issue: false hasContentIssue false
  • English
  • Français

Bisymmetric functions, Macdonald polynomials and basic hypergeometric series

Part of: Algebraic combinatorics Basic hypergeometric functions

Published online by Cambridge University Press:  01 March 2008

S. Ole Warnaar
S. Ole Warnaar*
Affiliation:
Department of Mathematics and Statistics, The University of Melbourne, VIC 3010, Australia (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

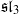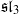A new type of basic hypergeometric series based on Macdonald polynomials is introduced. Besides a pair of Macdonald polynomials attached to two different sets of variables, a key ingredient in the 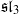basic hypergeometric series is a bisymmetric function related to Macdonald’s commuting family of q-difference operators, to the 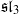Selberg integrals of Tarasov and Varchenko, and to alternating sign matrices. Our main result for 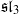series is a multivariable generalization of the celebrated q-binomial theorem. In the limit this q-binomial sum yields a new 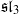Selberg integral for Jack polynomials.

Keywords

basic hypergeometric seriesMacdonald polynomialssl3 Selberg integrals

MSC classification

Secondary: 05E05: Symmetric functions and generalizations 33D67: Basic hypergeometric functions associated with root systems
Type
Research Article
Information
Compositio Mathematica , Volume 144 , Issue 2 , March 2008 , pp. 271 - 303
Copyright
Copyright © Foundation Compositio Mathematica 2008

References

Work supported by the Australian Research Council.