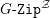Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T14:28:52.568Z Has data issue: false hasContentIssue false
  • English
  • Français

Automorphic vector bundles with global sections on $G\text{-}\mathtt{Zip}^{{\mathcal{Z}}}$-schemes

Part of: Discontinuous groups and automorphic forms Algebraic groups

Published online by Cambridge University Press:  31 October 2018

Wushi Goldring  and
Jean-Stefan Koskivirta
Wushi Goldring
Affiliation:
Department of Mathematics, Stockholm University, Stockholm SE-10691, Sweden email [email protected]
Jean-Stefan Koskivirta
Affiliation:
Department of Mathematics, South Kensington Campus, Imperial College London, London SW7 2AZ, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A general conjecture is stated on the cone of automorphic vector bundles admitting nonzero global sections on schemes endowed with a smooth, surjective morphism to a stack of 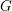$G$-zips of connected Hodge type; such schemes should include all Hodge-type Shimura varieties with hyperspecial level. We prove our conjecture for groups of type 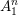$A_{1}^{n}$, 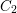$C_{2}$, and 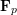$\mathbf{F}_{p}$-split groups of type 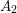$A_{2}$ (this includes all Hilbert–Blumenthal varieties and should also apply to Siegel modular 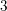$3$-folds and Picard modular surfaces). An example is given to show that our conjecture can fail for zip data not of connected Hodge type.

Keywords

G-zipsHasse invariantsShimura varietiesautomorphic vector bundles

MSC classification

Primary: 11F33: Congruences for modular and $p$-adic modular forms 11F46: Siegel modular groups; Siegel and Hilbert-Siegel modular and automorphic forms 14L30: Group actions on varieties or schemes (quotients)
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 12 , December 2018 , pp. 2586 - 2605
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andreatta, F. and Goren, E., Hilbert modular varieties of low dimension , in Geometric aspects of Dwork theory eds Adolphson, A., Baldassari, F., Berthelot, P., Katz, N. and Loeser, F. (Walter de Gruyter, Berlin, 2004), 113–175.Google Scholar
Boxer, G., Torsion in the coherent cohomology of Shimura varieties and Galois representations, PhD thesis, Harvard University, Cambridge, MA (2015).Google Scholar
Diamond, F. and Kassaei, P. L., Minimal weights of Hilbert modular forms in characteristic p , Compos. Math. 153 (2017), 1769–1778.Google Scholar
Goldring, W. and Koskivirta, J.-S., Strata Hasse invariants, Hecke algebras and Galois representations, Preprint, https://sites.google.com/site/wushijig/.Google Scholar
Goldring, W. and Koskivirta, J.-S., Zip stratifications of flag spaces and functoriality, Int. Math. Res. Not. IMRN, doi:10.1093/imrn/rnx229.Google Scholar
Goren, E., Hasse invariants for Hilbert modular varieties , Israel J. Math. 122 (2001), 157–174.Google Scholar
Green, M., Griffiths, P. and Kerr, M., Mumford–Tate groups and domains: their geometry and arithmetic, Annals of Mathematics Studies, vol. 183 (Princeton University Press, Princeton, NJ, 2012).Google Scholar
Jantzen, J., Representations of algebraic groups, Mathematical Surveys and Monographs, vol. 107, second edition (American Mathematical Society, Providence, RI, 2003).Google Scholar
Kisin, M., Honda–Tate theory for Shimura varieties, Oberwolfach Report No. 39/2015, ‘Reductions of Shimura varieties’.Google Scholar
Koskivirta, J.-S., Canonical sections of the Hodge bundle over Ekedahl–Oort strata of Shimura varieties of Hodge type , J. Algebra 449 (2016), 446–459.Google Scholar
Koskivirta, J.-S. and Wedhorn, T., Generalized 𝜇-ordinary Hasse invariants , J. Algebra 502 (2018), 98–119.Google Scholar
Lan, K.-W. and Stroh, B., Compactifications of subschemes of integral models of Shimura varieties, Forum Math. Sigma, to appear.Google Scholar
Lee, D., Nonemptiness of Newton strata of Shimura varieties of Hodge type , Algebra Number Theory 12 (2018), 259–283.Google Scholar
Madapusi Pera, K., Toroidal compactifications of integral models of Shimura varieties of Hodge type, Preprint (2018), arXiv:1211.1731v6.Google Scholar
Moonen, B., Group schemes with additional structures and Weyl group cosets , in Moduli of abelian varieties (Texel Island, 1999), Progress in Mathematics, vol. 195 (Birkhäuser, Basel, 2001), 255–298.Google Scholar
Moonen, B. and Wedhorn, T., Discrete invariants of varieties in positive characteristic , Int. Math. Res. Not. IMRN 72 (2004), 3855–3903.Google Scholar
Moret-Bailly, L., Pinceaux de Variétés abéliennes, Asterisque, vol. 129 (Société Mathématique de France, Paris, 1985).Google Scholar
Nie, S., Fundamental elements of an affine Weyl group , Math. Ann. 362 (2015), 485–499.Google Scholar
Ogus, A., Singularities of the height strata in the moduli of K3 surfaces , in Moduli of abelian varieties (Texel Island, 1999), Progress in Mathematics, vol. 195 (Birkhäuser, Basel, 2001), 325–343.Google Scholar
Oort, F., A stratification of a moduli space of abelian varieties , in Moduli of abelian varieties (Texel Island, 1999), Progress in Mathematics, vol. 195 (Birkhäuser, Basel, 2001), 345–416.Google Scholar
Pink, R., Wedhorn, T. and Ziegler, P., Algebraic zip data , Doc. Math. 16 (2011), 253–300.Google Scholar
Pink, R., Wedhorn, T. and Ziegler, P., F-zips with additional structure , Pacific J. Math. 274 (2015), 183–236.Google Scholar
Zhang, C., Ekedahl–Oort strata for good reductions of Shimura varieties of Hodge type , Canad. J. Math. 70 (2018), 451–480.Google Scholar