Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-02-16T16:16:33.311Z Has data issue: false hasContentIssue false
  • English
  • Français

Around 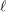$\ell$-independence

Part of: (Co)homology theory Arithmetic algebraic geometry

Published online by Cambridge University Press:  17 October 2017

Bruno Chiarellotto  and
Christopher Lazda
Bruno Chiarellotto
Affiliation:
Dipartimento di Matematica ‘Tullio Levi-Civita’, Università Degli Studi di Padova, Via Trieste 63, 35121 Padova, Italia email [email protected]
Christopher Lazda
Affiliation:
Dipartimento di Matematica ‘Tullio Levi-Civita’, Università Degli Studi di Padova, Via Trieste 63, 35121 Padova, Italia email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article we study various forms of 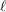$\ell$-independence (including the case 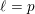$\ell =p$) for the cohomology and fundamental groups of varieties over finite fields and equicharacteristic local fields. Our first result is a strong form of 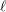$\ell$-independence for the unipotent fundamental group of smooth and projective varieties over finite fields. By then proving a certain ‘spreading out’ result we are able to deduce a much weaker form of 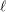$\ell$-independence for unipotent fundamental groups over equicharacteristic local fields, at least in the semistable case. In a similar vein, we can also use this to deduce 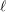$\ell$-independence results for the cohomology of smooth and proper varieties over equicharacteristic local fields from the well-known results on 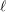$\ell$-independence for smooth and proper varieties over finite fields. As another consequence of this ‘spreading out’ result we are able to deduce the existence of a Clemens–Schmid exact sequence for formal semistable families. Finally, by deforming to characteristic 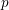$p$, we show a similar weak version of 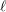$\ell$-independence for the unipotent fundamental group of a semistable curve in mixed characteristic.

Keywords

local function fieldscohomologyL-functionsmotivesunipotent fundamental groups

MSC classification

Primary: 11G20: Curves over finite and local fields
Secondary: 14F99: None of the above, but in this section
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 1 , January 2018 , pp. 223 - 248
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, T. and Caro, D., Theory of weights in  $p$ -adic cohomology, Preprint (2014), arXiv:1303.0662.Google Scholar
Andreatta, F., Iovita, A. and Kim, M., A p-adic nonabelian criterion for good reduction of curves , Duke Math. J. 164 (2015), 2597–2642, doi:10.1215/00127094-3146817.CrossRefGoogle Scholar
Berthelot, P., D-modules arithmétiques. I. Opérateurs différentiels de niveau fini , Ann. Sci. Éc. Norm. Supér. (4) 29 (1996), 185–272; http://www.numdam.org/item?id=ASENS_1996_4_29_2_185_0.CrossRefGoogle Scholar
Berthelot, P., Introduction à la théorie arithmétique des D-modules , in Cohomologies p-adiques et applications arithmétiques, II, Astérisque, vol. 279 (Société Mathématique de France, Paris, 2002), 1–80.Google Scholar
Caro, D., Comparaison des fonctuers duaux des isocristaux surconvergents , Rend. Semin. Mat. Univ. Padova 114 (2005), 131–211; http://www.numdam.org/item?id=RSMUP_2005__114__131_0.Google Scholar
Caro, D., Fonctions L associées aux D-modules arithmétiques. Cas des courbes , Compositio Math. 142 (2006), 169–206, doi:10.1112/S0010437X05001880.CrossRefGoogle Scholar
Chiarellotto, B. and Le Stum, B., Pentes en cohomologie rigide et F-isocristaux unipotents , Manuscripta Math. 100 (1999), 455–468, doi:10.1007/s002290050212.CrossRefGoogle Scholar
Chiarellotto, B. and Tsuzuki, N., Clemens-Schmid exact sequence in characteristic p , Math. Ann. 358 (2014), 971–1004, doi:10.1007/s00208-013-0980-8.CrossRefGoogle Scholar
Crew, R., F-isocrystals and p-adic representations , in Algebraic geometry, Bowdoin, 1985 (Brunswick, Maine, 1985), Proceedings of Symposia in Pure Mathematics, vol. 46 (American Mathematical Society, Providence, RI, 1987), 111–138, doi:10.1090/pspum/046.2/927977.Google Scholar
Crew, R., Finiteness theorems for the cohomology of an overconvergent isocrystal on a curve , Ann. Sci. Éc. Norm. Supér. 31 (1998), 717–763, doi:10.1016/S0012-9593(99)80001-9.CrossRefGoogle Scholar
Crew, R., Arithmetic D-modules on the unit disc , Compositio Math. 148 (2012), 227–268, doi:10.1112/S0010437X11005471.Google Scholar
de Jong, A. J., Smoothness, semi-stability and alterations , Publ. Math. Inst. Hautes Études Sci. 83 (1996), 51–93; http://www.numdam.org/item?id=PMIHES_1996__83__51_0.Google Scholar
Deligne, P., Les constantes des équations fonctionnelles des fonctions L , in Modular functions of one variable, II (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972), Lecture Notes in Mathematics, vol. 349 (Springer, Berlin, 1973), 501–597.Google Scholar
Deligne, P., La conjecture de Weil. I , Publ. Math. Inst. Hautes Études Sci. 43 (1974), 273–307; http://www.numdam.org/item?id=PMIHES_1974__43__273_0.CrossRefGoogle Scholar
Deligne, P., La conjecture de Weil. II , Publ. Math. Inst. Hautes Études Sci. 52 (1980), 137–252; http://www.numdam.org/item?id=PMIHES_1980__52__137_0.Google Scholar
Déglise, F. and Nizioł, W., On  $p$ -adic absolute Hodge cohomology and syntomic coefficients, I, Comment. Math. Helv., to appear. Preprint (2015), arXiv:1508.02567.Google Scholar
Etesse, J.-Y. and Le Stum, B., Fonctions L associées aux F-isocristaux surconvergents. I. Interpretation cohomologique , Math. Ann. 296 (1993), 557–576, doi:10.1007/BF01445120.Google Scholar
Fontaine, J.-M., Représentations ℓ-adiques potentiallement semi-stables , in Périodes p-adiques (Bures-sur-Yvette, 1988), Astérisque, vol. 223 (Société Mathématique de France, Paris, 1994), 321–347.Google Scholar
Hyodo, O. and Kato, K., Semi-stable reduction and crystalline cohomology with logarithmic poles , in Périodes p-adiques (Bures-sur-Yvette, 1988), Astérisque, vol. 223 (Société Mathématique de France, Paris, 1994), 221–268.Google Scholar
Ito, T., Weight-monodromy conjecture over equal characteristic local fields , Amer. J. Math. 127 (2005), 647–658, doi:10.1353/ajm.2005.0022.CrossRefGoogle Scholar
Kato, F., Log smooth deformation theory , Tohoku Math. J. 48 (1996), 317–354, doi:10.2748/tmj/1178225336.Google Scholar
Katz, N. M. and Messing, W., Some consequences of the Riemann hypothesis for varieties over finite fields , Invent. Math. 23 (1974), 73–77, doi:10.1007/BF01405203.Google Scholar
Kedlaya, K. S., Fourier transforms and p-adic ‘Weil II’ , Compositio Math. 142 (2006), 1426–1450, doi:10.1112/S0010437X06002338.CrossRefGoogle Scholar
Kleiman, S. L., Algebraic cycles and the Weil conjectures , in Dix exposés sur la cohomologie des schémas, Advanced Studies in Pure Mathematics, vol. 3 (North-Holland, Amsterdam, 1968), 359–386.Google Scholar
Lazda, C., Relative fundamental groups and rational points , Rend. Semin. Mat. Univ. Padova 134 (2015), 1–45, doi:10.4171/RSMUP/134-1.Google Scholar
Lazda, C., Fundamental groups and good reduction criteria for curves over positive characteristic local fields, J. Théor. Nombres Bordeaux, to appear. Preprint (2016), arXiv:1604.06024.Google Scholar
Lazda, C. and Pál, A., Rigid Cohomology over Laurent Series Fields, Algebra and Applications, vol. 21 (Springer, Cham, Switzerland, 2016), doi:10.1007/978-3-319-30951-4.Google Scholar
Lepage, E., Covers in p-adic analytic geometry and log covers I: Cospecialization of the (p ′ )-tempered fundamental group for a family of curves , Ann. Inst. Fourier (Grenoble) 63 (2013), 1427–1467, doi:10.5802/aif.2807.Google Scholar
Mannisto, P. and Olsson, M. C., Independence of  $\ell$  and surfaces, Preprint,https://math.berkeley.edu/∼molsson/surfaces4.pdf.Google Scholar
Marmora, A., Facteurs epsilon p-adiques , Compositio Math. 144 (2008), 439–483, doi:10.1112/S0010437X07002990.Google Scholar
Matsuda, S. and Trihan, F., Image directe supérieure et unipotence , J. Reine Angew. Math. 469 (2004), 47–54, doi:10.1515/crll.2004.028.Google Scholar
Nakayama, C., Nearby cycles for log smooth families , Compositio Math. 112 (1998), 45–75, doi:10.1023/A:1000327225021.CrossRefGoogle Scholar
Ogus, A., F-isocrystals and de Rham cohomology II – Convergent isocrystals , Duke Math. J. 51 (1984), 765–850, doi:10.1215/S0012-7094-84-05136-6.Google Scholar
Pridham, J., Weight decompositions on étale fundamental groups , Amer. J. Math. 131 (2009), 869–891, doi:10.1353/ajm.0.0055.Google Scholar
Grothendieck, A., Augmenté d’un exposé par Michèle Raynaud, Séminaire de Géométrie Algébrique du Bois-Marie, 1962 , in Cohomologie locale des faisceaux cohérents et théorèmes de Lefschetz locaux et globaux (SGA 2), Advanced Studies in Pure Mathematics, vol. 2 (North-Holland/Mason, Amsterdam/Paris, 1968).Google Scholar
Illusie, L. (ed.), Cohomologie l-adique et fonctions L , inSéminaire de Géometrie Algébrique du Bois-Marie 1965–1966 (SGA 5), Lecture Notes in Mathematics, vol. 589 (Springer, Berlin, 1977), doi:10.1007/BFb0096802.Google Scholar
Shiho, A., Crystalline fundamental groups I: Isocrystals on log crystalline site and log convergent site , J. Math. Sci. Univ. Tokyo 7 (2000), 509–656; http://www.ms.u-tokyo.ac.jp/journal/abstract_e/jms070401_e.html.Google Scholar
Tsuzuki, N., Slope filtration of quasi-unipotent overconvergent F-isocrystals , Ann. Inst. Fourier (Grenoble) 48 (1998), 379–412, http://www.numdam.org/item?id=AIF_1998__48_2_379_0.Google Scholar
Virrion, A., Dualité locale et holonomie pour les D-modules arithmétiques , Bull. Soc. Math. France 128 (2000), 1–68; http://www.numdam.org/item?id=BSMF_2000__128_1_1_0.Google Scholar
Zheng, W., Sur l’indépendance de l en cohomologie l-adique sur les corps locaux , Ann. Sci. Éc. Norm. Supér. (4) 42 (2009), 291–334.Google Scholar