Published online by Cambridge University Press: 20 October 2017
We provide lower bounds for 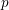 $p$-adic valuations of multisums of factorial ratios which satisfy an Apéry-like recurrence relation: these include Apéry, Domb and Franel numbers, the numbers of abelian squares over a finite alphabet, and constant terms of powers of certain Laurent polynomials. In particular, we prove Beukers’ conjectures on the
$p$-adic valuations of multisums of factorial ratios which satisfy an Apéry-like recurrence relation: these include Apéry, Domb and Franel numbers, the numbers of abelian squares over a finite alphabet, and constant terms of powers of certain Laurent polynomials. In particular, we prove Beukers’ conjectures on the 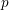 $p$-adic valuation of Apéry numbers. Furthermore, we give an effective criterion for a sequence of factorial ratios to satisfy the
$p$-adic valuation of Apéry numbers. Furthermore, we give an effective criterion for a sequence of factorial ratios to satisfy the 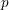 $p$-Lucas property for almost all primes
$p$-Lucas property for almost all primes 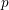 $p$.
$p$.