Published online by Cambridge University Press: 01 March 2008
Given a curve of genus 3 with an unramified double cover, we give an explicit description of the associated Prym variety. We also describe how an unramified double cover of a non-hyperelliptic genus 3 curve can be mapped into the Jacobian of a curve of genus 2 over its field of definition and how this can be used to perform Chabauty- and Brauer–Manin-type calculations for curves of genus 5 with an fixed-point-free involution. As an application, we determine the rational points on a smooth plane quartic and give examples of curves of genus 3 and 5 violating the Hasse principle. The methods are, in principle, applicable to any genus 3 curve with a double cover. We also show how these constructions can be used to design smooth plane quartics with specific arithmetic properties. As an example, we give a smooth plane quartic with all 28 bitangents defined over 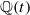 . By specialization, this also gives examples over
. By specialization, this also gives examples over 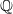 .
.
The research in this paper is partially supported by NSERC.