Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-22T12:42:43.010Z Has data issue: false hasContentIssue false
  • English
  • Français

The arc space of horospherical varieties and motivic integration

Part of: Special varieties Algebraic groups

Published online by Cambridge University Press:  19 June 2013

Victor Batyrev  and
Anne Moreau
Victor Batyrev
Affiliation:
Mathematisches Institut, Universität Tübingen, 72076 Tübingen, Germany email [email protected]
Anne Moreau
Affiliation:
Laboratoire de Mathématiques et Applications, Université de Poitiers, France email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For an arbitrary connected reductive group 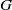$G$, we consider the motivic integral over the arc space of an arbitrary 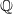$ \mathbb{Q} $-Gorenstein horospherical 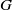$G$-variety 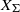${X}_{\Sigma } $ associated with a colored fan 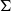$\Sigma $ and prove a formula for the stringy 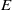$E$-function of 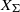${X}_{\Sigma } $ which generalizes the one for toric varieties. We remark that, in contrast to toric varieties, the stringy 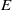$E$-function of a Gorenstein horospherical variety 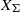${X}_{\Sigma } $ may be not a polynomial if some cones in 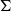$\Sigma $ have nonempty sets of colors. Using the stringy 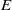$E$-function, we can formulate and prove a new smoothness criterion for locally factorial horospherical varieties. We expect that this smoothness criterion holds for arbitrary spherical varieties.

Keywords

horospherical varietyarc spacemotivic integrationstringy invariant

MSC classification

Secondary: 14L30: Group actions on varieties or schemes (quotients) 14M27: Compactifications; symmetric and spherical varieties
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 8 , August 2013 , pp. 1327 - 1352
Copyright
© The Author(s) 2013 

References

Batyrev, V., Stringy Hodge numbers of varieties with Gorenstein canonical singularities, in Integrable systems and algebraic geometry (Kobe/Kyoto, 1997) (World Scientific, River Edge, NJ, 1998), 1–32.Google Scholar
Batyrev, V., Non-Archimedean integrals and stringy Euler numbers of log-terminal pairs, J. Eur. Math. Soc. (JEMS) 1 (1999), 5–33.CrossRefGoogle Scholar
Bourbaki, N., Lie groups and Lie algebras, Chapters 4–6 (Springer, Berlin, 2002), translated from the 1968 French original by Andrew Pressley.Google Scholar
Brion, M., Groupe de Picard et nombres caractéristiques des variétés sphériques, Duke Math. J. 58 (1989), 397–424.Google Scholar
Brion, M., Sur la géométrie des variétés sphériques, Comment. Math. Helv. 66 (1991), 237–262.Google Scholar
Brion, M., Spherical varieties and Mori theory, Duke Math. J. 72 (1993), 369–404.Google Scholar
Brion, M., Curves and divisors in spherical varieties, in Algebraic groups and Lie groups, Australian Mathematical Society Lecture Series, vol. 9 (Cambridge University Press, Cambridge, 1997), 21–34.Google Scholar
Craw, A., An introduction to motivic integration (American Mathematical Society, Providence, RI, 2004), 203–225.Google Scholar
Danilov, V. I., The geometry of toric varieties, Uspekhi Mat. Nauk 33 (1978), 85–134.Google Scholar
Denef, J. and Loeser, F., Germs of arcs on singular varieties and motivic integration, Invent. Math. 135 (1999), 201–232.CrossRefGoogle Scholar
Docampo, R., Arcs on determinantal varieties, PhD thesis, University of Illinois at Chicago (2009).Google Scholar
Ein, L. and Mustaţă, M., Jet schemes and singularities, in Algebraic geometry: Seattle 2005, Proceedings of Symposia in Pure Mathematics, vol. 80, part 2 (American Mathematical Society, Providence, RI, 2009), 505–546.Google Scholar
Gaitsgory, D. and Nadler, D., Spherical varieties and Langlands duality, Mosc. Math. J. 10 (2010), 65–137.CrossRefGoogle Scholar
Ishii, S., The arc space of a toric variety, J. Algebra 278 (2004), 666–683.CrossRefGoogle Scholar
Kawamata, Y., Matsuda, K. and Matsuki, K., Introduction to the minimal model program, in Algebraic geometry: Sendai 1985, Advanced Studies in Pure Mathematics, vol. 10 (North-Holland, Amsterdam, 1987), 283–360.CrossRefGoogle Scholar
Knop, F., The Luna–Vust theory of spherical embeddings, in Proceedings of the Hyderabad Conference on Algebraic Groups (Hyderabad, 1989) (Manoj Prakashan, Chennai, 1991), 225–249.Google Scholar
Kontsevich, M., Motivic integration, Lecture at Orsay (1995), http://www.mabli.org/old/jet-preprints/Kontsevich-MotIntNotes.pdf.Google Scholar
Kostant, B., The principal three-dimensional subgroup and the Betti numbers of a complex simple Lie group, Amer. J. Math. 81 (1959), 973–1032.Google Scholar
Luna, D. and Vust, T., Plongements d’espace homogènes, Comment. Math. Helv. 58 (1983), 186–245.Google Scholar
Mustaţă, M., Jet schemes of locally complete intersection canonical singularities, Invent. Math. 145 (2001), 397–424; with an appendix by D. Eisenbud and E. Frenkel.Google Scholar
Onishchik, A. L. and Vinberg, E. B., Lie groups and algebraic groups, Springer Series in Soviet Mathematics (Springer, Berlin, 1990), translated from the Russian and with a preface by D. A. Leites.Google Scholar
Pasquier, B., Variétés horosphériques de Fano, PhD thesis, Université Joseph Fourier – Grenoble I (2006), http://tel.archives-ouvertes.fr/tel-00111912.Google Scholar
Pauer, F., Normale Einbettungen von $G/ U$, Math. Ann. 257 (1981), 371–396.Google Scholar
Pauer, F., Glatte Einbettungen von $G/ U$, Math. Ann. 262 (1983), 421–429.Google Scholar
Sankaran, P. and Uma, V., Cohomology of toric bundles, Comment. Math. Helv. 78 (2003), 540–554.Google Scholar
Sumihiro, H., Equivariant completion, J. Math. Kyoto Univ. 14 (1974), 1–28.Google Scholar
Timashev, D., Homogeneous spaces and equivariant embeddings, Encyclopaedia of Mathematical Sciences, vol. 138. Invariant theory and algebraic transformation groups VIII (Springer, Heidelberg, 2011).Google Scholar
Veys, W., Arc spaces, motivic integration and stringy invariants, in Singularity theory and its applications (Sapporo, 2003), Advanced Studies in Pure Mathematics, vol. 43 (American Mathematical Society, Providence, RI, 2006), 529–572.Google Scholar